Shen S., Tuszynski J.A. Theory and Mathematical Methods for Bioformatics
Подождите немного. Документ загружается.

68 3 Modulus Structure Theory
corresponding expansion and compression are called the real expansion and
real compression, respectively.
2. Let A = {A
t
,t=1, 2, ··· ,m} be a set of sequences defined on V
4
. A then
represents the set of homologous expansions of A if all A
t
,t=1, 2, ··· ,m
are the expansions of A. A sequence D is called the core of the set A if D
is the common compression of all sequences in A. Similarly, for multiple
sequences A, a sequence C is called the envelope of A if each sequence in
A is a compressed sequence of C.
3. D
0
is the maximal core of A if D
0
isthecoreofA and any real larger
expansion of D
0
is not the core of A. The longest maximal core is called
the maximum core. Similarly, a sequence C
0
is the minimal envelope of
A if it is the envelope of A and any real compression of C
0
will not be an
envelope of A. The smallest such envelope is called the minimum envelope.
If A is a subsequence of C, then there is a subset α = { j
1
,j
2
, ··· ,j
n
a
} of N
c
such that 1 ≤ j
1
<j
2
< ···<j
n
a
≤ n
c
,and
c
α
=(c
j
1
,c
j
2
, ···c
j
n
a
)=(a
1
,a
2
, ···a
n
a
)=A. (3.1)
This set α represents the positions if A is embedded into C.Letα
c
= N
c
−α
be the complementary subset of α,thenB = c
α
c
is nothing but the virtual
symbol “−” to get the expansion of A,inwhich,c
α
c
=(c
j
,j∈ α
c
). If α ⊂ N
c
,
and C =(c
α
,c
α
c
)=(A, B), then the binary (A, B) is a decomposition of
C, and they are both compressions of C. If sequence C is defined on V
5
=
{0, 1, 2, 3, 4}, then the virtual expanded sequence C based on A is defined in
Definition 2.
Modulus Structure of Expanded Sequence
and Compressed Sequence
If A is a subsequence of sequence C, then the relationship between A and C
can be described by (3.1). However, (3.1) becomes too complex as the lengths
of sequences A and C increase. To simplify the description, we introduce some
definitions and notations as follows:
K
c
=(j
0
,j
1
,j
2
, ··· ,j
2k
c
−1
,j
2k
c
) , (3.2)
in which 0 = j
0
≤ j
1
<j
2
< ··· <j
2k
c
≤ j
2k
c
+1
= n
c
.ThenN
c
can be
subdivided into many smaller intervals as follows:
δ
k
=[j
k
+1,j
k+1
]=(j
k
+1,j
k
+2, ··· ,j
k+1
) k =0, 1, 2, ··· , 2k
c
. (3.3)
Based on these small intervals δ
k
, we define
Δ
1
=
δ
1
,δ
3
, ··· ,δ
2k
c
−1
,
Δ
2
=
δ
0
,δ
2
, ··· ,δ
2k
c
.
(3.4)
3.1 Modulus Structure of Expanded and Compressed Sequences 69
Therefore, N
c
=(Δ
1
,Δ
2
). The binary (Δ
1
,Δ
2
) is a decomposition of N
c
and
is determined by K. It suffices to show that Δ
1
∩Δ
2
= φ is an empty set and
Δ
1
∪ Δ
2
= N
c
.
Definition 11. 1. If K
c
is defined by (3.2) and the decomposition of K
c
is
defined by (3.4), satisfying the following condition:
c
Δ
1
=
c
δ
1
,c
δ
3
, ··· ,c
δ
2k
c
−1
= A, (3.5)
then K
c
is the expanded mode from A to C or the compressed mode from
C to A,wherec
δ
k
=(c
j
k
+1
,c
j
k
+2
, ··· ,c
j
k+1
) is a subvector of C restricted
to the interval δ
k
.
2. The pairwise sequence (A, B) in (3.4) is a decomposition of C and the
sequence C is an expansion of both A and B. K is a decomposition mode
of C related to (A, B), if (3.5) and (3.6) are satisfied.
c
Δ
2
=
c
δ
2
,c
δ
4
, ··· ,c
δ
2k
c
= B (3.6)
3. If C is a sequence defined on V
5
and A is a sequence defined on V
4
such
that C =(A, B) and B =(4, 4, ··· , 4) is a sequence of virtual symbols,
then C is a virtual expansion of A,andK is the virtually expanded mode
for A virtually expanding to C.
Operations for Position-Shifting in Expanded
and Compressed Sequences
We add some new notations in (3.2) as follows:
k
= j
2k+1
− j
2k
,L
k
=
k−1
k
=1
k
,i
k
= j
2k−1
− L
k
. (3.7)
Then
k
is the length of the kth inserted vector and L
k
is the shifting func-
tion resulting from insertions. If the expanded mode K
c
is known, then the
relationship between A and C will be determined by K
c
,asshownbythe
following theorem.
Theorem 8. If C is an expanded sequence of A under the expanded mode K
c
,
then
A =
a
δ
1
,a
δ
2
, ··· ,a
δ
k
c
=
c
δ
1
,c
δ
3
, ··· ,c
δ
2k
c
−1
(3.8)
in which a
δ
k
= c
δ
2k−1
and
δ
k
= δ
2k−1
− L
k
=[i
k
+1,i
k+1
]=(i
k
+1,i
k
+2, ··· ,i
k+1
) . (3.9)
Proof. Since C is an expansion of A, it suffices to prove that the second
equation of (3.6) and (3.8) hold. Changing A =(a
1
,a
2
, ··· ,a
n
a
)intothe
form of (3.8) gives a
δ
k
= c
δ
2k−1
. Since the distance between the intervals
δ
2k−1
and δ
2k+1
is
k
, it follows that (3.9) holds, which concludes the proof.
70 3 Modulus Structure Theory
Equation (3.9) is the position-shifting formula of expanded sequences in the
following text.
The Equivalent Representations of Modes
If K
c
is given, then the function (i
k
,
k
,L
k
) is determined by (3.7). Let
H
a
= {(i
k
,
k
),k=1, 2, ··· ,k
c
} (3.10)
be the modulus structure expanding A to C. H
a
is then the set of all orders
describing how to expand A. Typically, the order (i
k
,
k
)meansthatweinsert
a vector with length
k
following the position i
k
. Notice how this is represented
in K
c
and H
a
. Here, K
c
targets the positions of C, while H
a
is targeting the
positions of A. Therefore, we use different subscripts to differentiate them in
the following.
Theorem 9. The expanded modes K
c
and the modulus structure H
a
are equiv-
alent.
Proof. Following from (3.7) and (3.10), we know that H
a
is determined if K
c
is
given. Consequently, it is sufficient to show that K
c
is also determined by H
a
.
L
k
is then determined by
k
and the second equation of (3.7) if H
a
is given.
Thus, it follows from (3.10) that j
2k−1
is determined for all k =1, 2, ···,k
c
.
We can use the first equation of (3.7) to calculate all j
2k
using the formula
j
2k
= j
2k+1
−
k
for all k =1, 2, ··· ,k
c
. Therefore, each of K
c
and H
a
is
determined by the other, concluding the proof.
Let I
a
= {i
k
: k =1, 2, ··· ,k
c
} be the set of all positions after which vectors
will be inserted. This is the set of inserting positions to get the expanded
sequence C. There is then an alternative expression of H
a
as follows:
H
a
=(γ
0
,γ
1
,γ
2
, ··· ,γ
n
a
) (3.11)
in which γ
i
∈ V
0
= {0, 1, 2, ···} and
γ
i
=
k
if i = i
k
∈ I
a
,
0otherwise.
γ
j
= 0 implies that there will be no virtual symbols inserted after j,andγ
j
> 0
means there is a virtual symbol of length γ
j
inserted after j.Itisobvious
that H
a
and H
a
determine each other. Consequently, K
c
,H
a
and H
a
are all
equivalent. The modulus structure of the expanded sequence is demonstrated
in Fig. 3.1. Due to their equivalence we do not need to distinguish these names.
In Fig. 3.1, C is the expanded sequence of A. The original part A and
the expanded part are represented by different line segments, where i
k
,δ
k
are
positions and intervals of sequence A respectively, j
k
,δ
k
are positions and
intervals of sequence C, respectively, and where
k
= |δ
2k
| is the length of δ
2k
.
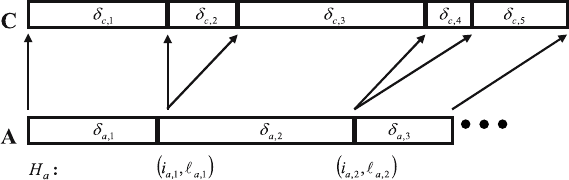
3.1 Modulus Structure of Expanded and Compressed Sequences 71
Fig. 3.1. The modulus structure of the expanded sequence
The Modulus Structure of the Compressed Sequences
If C is the expanded sequence of A,thenA is the compressed sequence of C.
Let
H
c
= {(j
k
,
k
),k=1, 2, ··· ,k
c
} , (3.12)
in which j
k
= j
2k
,
k
= j
2k+1
− j
2k
is determined by K
c
of (3.2). It is then
referred to as the as compressed mode from C to A. This mode tells us how
to delete a vector of length
k
after position j
k
of C.
3.1.2 The Order Relation and the Binary Operators on the Set
of Expanded Modes
Let A be a sequence defined on V
4
. There will exist many expanded sequences
based on A. These expanded sequences are quite different if the inserted vec-
tors or expanding modes are different. In this section, we illustrate how to
compare these modes, and give the binary operators on the set of expanding
modes.
The Order Relation and the Binary Operators Defined on the Set
of Modes
Let C and C
be two expanded sequences based on A,andlet
H =(γ
0
,γ
1
,γ
2
, ··· ,γ
n
a
) ,H
=
γ
0
,γ
1
,γ
2
, ··· ,γ
n
a
be the two corresponding expanding modes. We can compare the two modes
by defining the “order relation” on the set of all modes as follows.
Definition 12. Denote a nonempty set of modes by H. We define an order
relation on H as follows: For any pair H, H
∈H, we can say that H ≤ H
or H ⊂ H
if and only if γ
j
≤ γ
j
for all j ∈{0, 1, 2, ··· ,n
a
}.
This order relation is quite natural. If we define this order relation “≤”onthe
set H consisting of all modes resulting from a given sequence A, it becomes
a semiordered set. We will discuss the properties of order relations in the next
72 3 Modulus Structure Theory
subsection. Here, we continue to give definitions of binary operators. Similarly
to the ordinary binary operators used in set theory, we can also define the
corresponding binary operators between any pair of modes H, H
∈H, e.g.,
intersection, union, and subtraction, etc.
Definition 13. If we let H, H
∈H, and construct new expanding modes as
below
H
=
γ
0
,γ
1
,γ
2
, ··· ,γ
n
a
,
then we have the following cases:
1. If γ
j
=min{γ
j
,γ
j
} for all j,thismodeH
is called the intersection of H
and H
, and is denoted by H
= H ∧H
.
2. If γ
j
=max{γ
j
,γ
j
} for all j,thismodeH
is called the union of H and
H
, and denoted by H
= H ∨ H
.
3. If γ
j
= γ
j
−γ
j
≥ 0 for all j, then this mode H
means that H
is subtracted
from H, and is denoted by H
= H − H
.
Based on these definitions, we may find that H ≤ H
is the necessary condition
for H
= H − H
to hold. Generally, subtraction for any pair of modes can
be defined as follows:
H
= H
\ H = H
− (H ∧H
) .
Furthermore, we can define the symmetric subtraction of H and H
as follows:
H
= HΔH
= H ∨H
− H ∧ H
.
The Properties of Order Relation and the Binary Operators
Theorem 10. If H is the set of all expanded modes of A, the relationships
defined by Definitions 12 and 13, such as the order relations “≤”, and the three
operations: union, intersection, and subtraction, make H a Boolean algebra.
Before proving this theorem, let us first discuss some additional properties.
Let H, H
,H
∈H, so that we have the properties for the order relation “≤”
as follows:
1. Transmissivity If H ≤ H
and H
≤ H
,thenH ≤ H
.
2. Reflexivity If H ≤ H and H ≤ H
,H
≤ H, H = H
.Thatis,H is
a semiordered set in this order relation.
3. Furthermore, the three operations: intersection, union, and subtraction,
satisfy the properties as follows:
(a) Closeness. For every H, H
∈H, the results of intersection, union
and subtraction are still in H.Thisis,H ∧H
∈H, H ∨ H
∈Hand
H \ H
∈H.
3.1 Modulus Structure of Expanded and Compressed Sequences 73
(b) Commutative law. For intersection and union, we have
H ∧ H
= H
∧ H, H∨ H
= H
∨ H.
(c) Associative law for union and intersection. For intersection and
union, the properties are as follows:
(H ∧H
) ∧H
= H ∧(H
∧H
) , (H ∨H
) ∨H
= H ∨(H
∨H
) .
(d) Distributive law. When the two operations of intersection and union
occur at the same time, we have
(H ∨ H
) ∧ H
=(H ∧ H
) ∨ (H
∧ H
) .
All six properties above can be easily validated using Definitions 12 and 13.
Theorem 10 is easily proved based on these properties, and consequently sat-
isfies the requirements of a Boolean algebra.
3.1.3 Operators Induced by Modes
The Operator Induced by Compressed Modes
Let C be an expanded sequence of A. Using (3.10) and (3.12), we obtain the
corresponding expanded mode H
a
(from A to C),andthecompressedmode
H
c
(from C to A). If C and the compressed mode H
c
are given, then A is
determined by (3.8). Consequently, A canbeconsideredtobetheresultof
having C acteduponbyanoperatorinducedbyH
c
. We denote this induced
operator by H
c
, and we then state that A = H
c
(C). This operator H
c
induced
by the compressed mode is called the compressed operator.
The Operator Induced by Expanded Modes
If the virtual expanded mode of A is given, then the virtual expanded se-
quence C is unique. Generally, if only A and its expanded mode H
a
are known,
then we may not be able to completely determine C because (3.8) can only
determine one part of C. If sequence B is the inserted part, we can induce an
operator H
a
based on H
a
as follows:
H
a
(A, B)=C =
a
δ
1,1
,b
δ
2,1
,a
δ
1,2
,b
δ
2,2
, ··· ,a
δ
1,h
a
,b
δ
2,h
a
(3.13)
in which δ
1,k
= δ
k
is defined by (3.8) and (3.9), and b
δ
2,k
is the insertion vector
of length
2,k
.Then
A =
a
δ
1,1
,a
δ
1,2
, ··· ,a
δ
1,k
a
,B=
b
δ
2,1
,b
δ
2,2
, ··· ,b
δ
2,k
b
(3.14)
follows from (3.13). That is, sequence C is determined by A, B,andH
a
.The
operator H
a
defined by (3.13) is called the expanded operator.
74 3 Modulus Structure Theory
Mutually Converse Operation Between the Expanded Mode
and the Compressed Mode
Theorem 11. If C is the virtual expanded sequence of A, and the expanded
mode and compressed mode H
a
and H
c
are defined in (3.10) and (3.12) sat-
isfying the following properties:
1. k
c
= k
a
,and
k
=
k
for all k =1, 2, ···,k
a
.
2. j
k
= i
k
+ L
k
for all k =1, 2, ···,k
a
,
then H
c
[H
a
(A)] = A and H
a
[H
c
(C)] = C will always hold.
This theorem can be proved using (3.8), (3.13), and (3.14) under condi-
tions (1–3).
Definition 14. If H
a
,H
c
are the modulus structures of A and C defined as in
(3.10) and (3.12), and if conditions 1–3 of Theorem 11 are satisfied, then H
a
is the inverse operator of the expanded operator and H
c
is the inverse operator
of the compressed operator. That is, H
a
= H
−1
c
, H
c
= H
−1
a
.
Operators Induced by Union on Expanded Modes
For any H, H
∈H,letH
= H
∨ H. The relationships among the three
operators H, H
, H
induced by H, H
,H
are stated as follows: First, we
notice that
H
(A, B)=H
[H(A, B)] (3.15)
does not hold because H(A, B) is not the same as the sequence A according to
(3.13), and the operator H
[H(A, B)] is much longer than H
(A, B) according
to the definition of H, H
, H
. Consequently, we must modify (3.13) to fit this
case. Without loss of generality, we may assume that all expanded positions
of H, H
,andH
are the same, that is,
⎧
⎪
⎨
⎪
⎩
H = {(i
k
,
k
) ,k=1, 2, ··· ,k
c
} ,
H
= {(i
k
,
k
) ,k=1, 2, ··· ,k
c
} ,
H
= {(i
k
,
k
) ,k=1, 2, ··· ,k
c
} ,
(3.16)
in which
k
=max{
k
,
k
} and 0 ≤
k
,
k
≤
k
. In addition, we reiterate the
following notations:
1. In C = H(A, B), sequence B =(B
1
,B
2
, ··· ,B
k
c
) is called the insertion
template. Each component B
k
is a vector inserted after the component a
i
k
of sequence A,anditslengthis
k
.
2. B
=(B
1
,B
2
, ··· ,B
k
c
) is called the expanded sequence of B if
k
≤
k
for
all k.Importantly,B
k
is empty if
k
=
k
. There is then a new sequence
formed as follows:
B
=
(B
1
,B
1
) , (B
2
,B
2
) , ··· ,
B
k
c
,B
k
c
.
3.1 Modulus Structure of Expanded and Compressed Sequences 75
3. Let H
c
= {(j
k
,
k
−
k
), k =1, 2, ··· ,k
c
},inwhichj
k
= i
k
+ L
k
and L
k
is defined by (3.7). Then, H
c
is an expanded mode of C = H(A, B).
With the above notations, we formulate the following theorem.
Theorem 12. If H, H
∈Hand H
= H
∨ H, then the expanded operators
induced by H, H
,H
satisfy the following relationship:
H
(A, B
)=H
c
[H(A, B),B
] . (3.17)
The proof of this theorem can be constructed using the definitions of H, H
c
, H
and notations 1–3.
Definition 15. H
c
defined in (3.17) is called the second expanded operator
of A,andj
k
= i
k
+ L
k
is called the shift of the second expanded operator.
Theorem 13. For every pair H
,H ∈H, H
= H
∨ H can be decomposed
into a second expanded operation. If both C and C
are virtual expanded se-
quences of A, then the corresponding expanded modes can be simplified so that
B
=(B, B
) is composed of virtual symbols q alone.
Example 5. Comparing the three sequences
⎧
⎪
⎨
⎪
⎩
A = (010201032213020103211022301) ,
C = (01020[210]103221302[11]010321[03]1022301) ,
C
= (01020[210]103221302[1100]010321[02231]1022301) ,
we can make the following observations:
1. Sequences C and C
are both expanded sequences of A, their lengths are
respectively: n
c
=34andn
c
= 39, and their expanded modes are stated
as follows:
H = {(5, 3), (14, 2), (20, 2)} = (0000030000000020000020000000) ,
H
= {(5, 3), (14, 4), (20, 5)} = (0000030000000040000050000000) .
2. H ≤ H
and
H
= H
− H = {(14, 2), (20, 3)} = (0000000000000020000030000000) .
C
can be seen as a second expanded partition of A as follows:
A
H
→ C
H
→ C
.
3. The shifting function of the accumulated length of (A, C)is
¯
L =(0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0, 7, 0, 0, 0, 0, 0, 0, 0) .
Therefore,
H
c
= H
− H = (000000[000]00000000[002]00000[0201]0000000)
in which all segments in the square brackets connected as 0000020201
comprise the second expanded mode of B.
76 3 Modulus Structure Theory
4. The virtual expanded mode H
c
in observation 3 can be simplified as
H
c
= H
− H = (000000[000]00000000[002]00000[003]0000000)
in which 000002003 composed from all segments in the brackets is just the
second expanded mode of B. This means that we must insert two virtual
symbols after position 5 and insert three virtual symbols after position 7.
3.2 Modulus Structure of Sequence Alignment
In Sect. 3.1, we mentioned that the result of a sequence alignment operation is
also a special sequence. For a set of sequences, the results of multiple alignment
are also special multiple sequences. We will elaborate on the description of
modulus structures for multiple alignment, since multiple alignment is an
important tool in analyzing sequence mutations.
3.2.1 Modulus Structures Resulting from Multiple Alignment
Let A be a set of sequences given in (3.1) and (3.2), defined on V
4
,andletA
be a set of sequences defined on V
5
similar to (1.4). Following the definition
of multiple alignment given in Definition 2, we have that A
s
is the virtual
expanded sequence of A
s
for all s ∈ M , and sequence a
s,j
,s=1, 2, ··· ,mhas
no two connected virtual symbols for all j. Below, we discuss its structure in
detail.
Representation of Modulus Structures Resulting from Multiple
Alignment
Based on the representation of the modulus structures resulting from a single
expanded sequence, we generate a representation to fit multiple alignment.
The two modes of multiple alignment are stated as follows:
H = {H
s
,s=1, 2, ··· ,m}, H
= {H
s
,s=1, 2, ··· ,m} , (3.18)
where
H
s
= {(i
s,k
,
s,k
),k=1, 2, ··· ,k
s
},H
s
=(γ
s,0
,γ
s,1
,γ
s,2
, ··· ,γ
s,n
s
) .
(3.19)
The notations in (3.19) are explained as follows:
1. n
s
is the length of sequence A
s
,andk
s
is the number of the inserted
vectors so that A
s
becomes A
s
.
2. In H
s
, i
s,k
is the starting position of the kth inserted vectors so that A
s
becomes A
s
,and
s,k
is the length of the kth inserted vector. In other
words,
s,k
virtual symbols are inserted after position i
s,k
in sequence A
s
.
3.2 Modulus Structure of Sequence Alignment 77
3. In H
s
, γ
s,i
≥ 0meansthatweinsertγ
s,i
symbols after the ith position.
Typically, γ
s,i
= 0 means that there is no symbol to be inserted, while
γ
s,i
> 0 means that we will insert γ
s,i
virtual symbols after position i.
4. Each of H and H
can be determined by the other. Based on H
s
,wecan
define I
s
= {i
s,k
,k=1, 2, ··· ,k
s
}.Then
γ
s,j
=
s,k
, if i = i
s,k
∈ I
s
,
0 , otherwise ,
(3.20)
and H determines H
.Conversely,H
can determine H as follows:
I
s
= {i ∈ N
s+
,γ
s,i
> 0},
s,i
k
= γ
s,i
, if i = i
k
∈ I
s
,
(3.21)
where N
s+
= {0, 1, 2, ···,n
s
,andn
s
is the length of sequence A
s
. Follow-
ing from (3.20) and (3.21), H and H
can be determined by each other.
H and H
are therefore representations of the modulus structures based
on A.
Representation of Modes Resulting from Alignments
Since A
is the expanded sequence of A, the alignment mode can be repre-
sented based on A
.Infact,
δ
s,k
=[j
s,k
+1,j
s,k+1
]=(j
s,k
+1,j
s,k
+2, ··· ,j
s,k+1
) , (3.22)
a
δ
s,k
=
a
s,j
s,k
+1
,a
s,j
s,k
+2
, ··· ,a
s,j
s,k+1
. (3.23)
If we let
K = {K
s
,s∈ M },K
s
= {j
s,1
,j
s,2
, ··· ,j
s,2k
s
} (3.24)
then
1. For every K
s
,wechoosej
s,k
+1,j
s,k
+2, ··· ,j
s,k+1
such that
1=j
s,0
≤ j
s,1
<j
s,2
< ···<j
s,2k
s
≤ j
s,2k
s
+1
= n
s
,
where n
s
is the length of sequence A
s
.
2. Since A
s
is the expanded sequence A
s
for all s, it means that all definitions
and properties and notations in Sect. 3.2 can be used here. For example,
the expanded sequence A
s
may be represented by
A
s
=
a
δ
s,1
,a
δ
s,2
, ··· ,a
δ
s,k
c
=
a
δ
s,1
,a
δ
s,3
, ··· ,a
δ
s,2k
c
−1
, (3.25)
where a
δ
s,k
= a
δ
s,2k−1
and
δ
s,k
=[i
s,k
+1,i
s,k+1
]=(i
s,k
+1,i
s,k
+2, ··· ,i
s,k+1
)
are determined by (3.18).
