Shen S., Tuszynski J.A. Theory and Mathematical Methods for Bioformatics

Подождите немного. Документ загружается.

2.2 Stochastic Models of Flow Raised by Sequence Mutations 37

in which N(0, 1) denotes a standard normal distribution and

= E





ξ, ˜η, i, j, n) −μ





⎧

⎪

⎨

⎪

⎩



a,b∈V

[w(a, b) − w

]

p(a, b) , if i = j,



a,b∈V

[w(a, b) − μ

]

, otherwise .

(2.23)

Proof. Following from Theorem 2, Lemma 1, the Kolmogorov law of large

numbers, and the Levy–Lindberg central limit theorem, when w(a, b)=

(a, b) is the Hamming function, then from Deﬁnition 3 of an independent

sequence pair, we calculate σ

as follows:

1. While i = j,



a,b∈V

[w(a, b) − w

]

p(a, b)=(1− )

+(1− )

 =(1− ).

2. While i = j,



a,b∈V

[w(a, b) − w

]





2.2 Stochastic Models of Flow Raised

by Sequence Mutations

A biological sequence is composed of many small molecular units, and se-

quence mutations most often result from the mutation of some of these units.

In stochastic processes, the structure of this type of mutation is usually dis-

cussed in two stages. First, we discuss how the mutations occur, and then

discuss the eﬀects of these mutations. It is similar to describing the arrival of

customers at a shop, and then describing how much these customers spend.

These two stages happen randomly. The stochastic process which describes

the occurrence of these mutations is referred to as the random ﬂow of muta-

tions or simply the ﬂow of mutations. There are four kinds of mutation eﬀects,

which may be described by the corresponding stochastic processes. Combining

the results from the two stages, we obtain the stochastic model of sequence

mutations.

2.2.1 Bernoulli Processes

Usually, random ﬂow is described by the Bernoulli process or the Poisson pro-

cess in probability theory. The common characteristic of these two processes is

that a random ﬂow is composed of many small probability independent events.

38 2 Stochastic Models of Mutations and Structural Analysis

For example, customers may arrive in a shop at diﬀerent times, and the num-

bers of customers arriving at a given time are independent. Generally, this

characteristic coincides with the characteristic of mutation ﬂow in a biologi-

cal sequence. Consequently, mutation ﬂow can be described by the Bernoulli

process or the Poisson process. The corresponding symbols deﬁnitions and

properties are given below.

Deﬁnition and Notations of the Bernoulli Process

The Bernoulli process is a stochastic sequence whose time and state are dis-

crete. If we denote it by

ζ =(ζ

,ζ

, ···), then it has the following charac-

teristics:

ζ is an independent sequence and each element ζ

is determined according

to the Bernoulli experiment. Here, each ζ

has only the value 0 or 1, which

denotes whether or not the event happens at time j.

2. The probability distribution of ζ

{ζ

=1} = 

{ζ =0} =1− 

. (2.24)

Here, ˜ =(

,

, ···) is called the strength sequence of the Bernoulli pro-

cess. If the strength sequence ˜ in (2.24) is a constant series ,then

ζ is called

an homogeneous Bernoulli process and  is the strength of the Bernoulli pro-

cess.

For simplicity, we will discuss only homogeneous Bernoulli processes. Since

the nonhomogeneous and nonindependent situations follow similar arguments,

we will omit them in this book.

Counting Process and Dual Renewal Processes Associated

with Bernoulli Processes

Let

ζ be a given homogeneous Bernoulli process, and let v

∗



j=1

be the

total number of mutations happening in region [1,n]. So ˜v

∗

= {v

∗

, ···}

is then referred to as the counting process. ˜v

∗

is also referred to as the renewal

process of

ζ in the sense of stochastic processes. The following characteristics

hold:

1. Let ˜v

∗

be a binomial, homogeneous, and independent increment process

and

∗



− v

∗

= k} = b(n



− n, k; )=



− n)!

k! ·(n



− n −k)!



(1 − )



−n−k

(2.25)

hold for all 0 ≤ n ≤ n



and all k =0, 1, 2, ···;herev

∗

≡ 0. The probability

distribution

b(n, k; )=

k! ·(n −k)!



(1 − )

n−k

,k=0, 1, 2, ···,n

is then a binomial distribution.

2.2 Stochastic Models of Flow Raised by Sequence Mutations 39

2. ˜v

∗

generates the dual renewal process of ˜v

∗

=sup{j : v

∗

≤ k} , (2.26)

in which j

∗

denotes the time at which the kth renewal happens in renewal

process theory. In this book, j

∗

denotes the position of the kth mutation.

Hence

∗

=(j

∗

, ···) (2.27)

is referred to as the mutation point sequence. It is equal to the sequence

of the renewal position in the renewal process, in which j

∗

≡ 0. A de-

tailed discussion about renewal sequences (or processes) and dual renewal

sequences (or processes) may be found in [25].

Characteristics of Dual Renewal Processes

The relationships and characteristics of the renewal process ˜v

∗

and its dual

renewal process

∗

are stated as follows:

1. The sequence

∗

is a homogeneous and independent incremental process.

If we let 

∗

= j

∗

−j

∗

k−1

,then



∗

= {

∗

,

∗

,

∗

, ···}is an i.i.d. sequence and

each 

∗

has a geometric distribution e



(n). That is,

∗

− j

∗

k−1

= n} = e

1−

(n)=(1 − )

n−1

,k,n=1, 2, 3, ··· . (2.28)

2. Following from the property of geometric distribution, we have that j

∗

a negative binomial distribution. That is,

∗

= n} = C

k−1

n−1



(1−)

n−k

(k − 1)!

(n −1)!(k − n)!



(1−)

n−k

,k≥ n.

(2.29)

3. Since the sequence ˜v

∗

is the dual renewal process of

∗

, it follows that

∗

=sup{k : j

∗

≤ n} (2.30)

holds.

Consequently, the four sequences

ζ,˜v

∗



∗

can be determined from each

other. Moreover,

ζ,



∗

are i.i.d. sequences that obey the Bernoulli distribu-

tion b



, and geometric distribution e



(k), respectively. Furthermore, ˜v

∗

and

∗

are the renewal processes of

ζ and



∗

respectively, where,

∗



j=1

∗



i=1



∗

Following from (2.26) and (2.30), we have that ˜v

∗

and

∗

are the dual renewal

processes for each other.

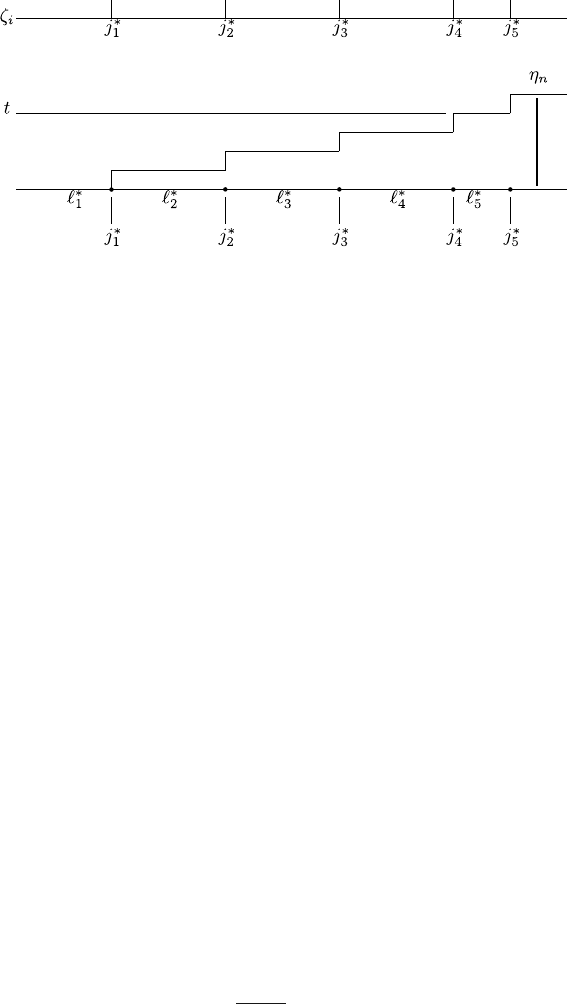
40 2 Stochastic Models of Mutations and Structural Analysis

Fig. 2.1. The Bernoulli process, the counting process, and its dual renewal process

These properties also can be found in textbooks on the theory of stochas-

tic processes, for example, in Doob’s book [25]. The relationships among se-

quences

ζ,˜v

∗



∗

are described in Fig. 2.1.

In Fig. 2.1,

ζ is a Bernoulli process. The top line denotes the value of ζ

as 0 or 1, in which, j

∗

, s =1, 2, 3, ··· denotes the positions held by ζ

=1.

The lowest line denotes the relationship between ζ

and η

. Following from

the deﬁnition of the dual renewal process, we have

∗

=sup{v : η

≤ s} = j

∗

,s=1, 2, 3, ···

and 

∗

= j

∗

− j

∗

s−1

2.2.2 Poisson Flow

The Poisson process is one of the most basic and important stochastic pro-

cesses describing mutation ﬂows. We recall its notations and properties below.

Deﬁnition and Generation of Poisson Flows

Poisson ﬂow (also called the Poisson process) is a stochastic process with se-

quential time and discrete states. Poisson ﬂow is a stochastic ﬂow composed of

an accumulation of many small probability events. It has three main character-

istics: the stationary property, the nonbackward property and the sparseness

property. Let v

∗

be the number of times that some event happens in interval

(0,s), then v

∗

(s, s + t)andv

∗

have the same distribution for all t>0. Then

∗

)andv

∗

) are independent if 0 ≤ s

. The probability

of the event happening twice or more in the interval (0, Δs) is inﬁnitesimal

in higher orders such that Δs is inﬁnitesimal. The probability distribution of

∗

(s) is then deﬁned by:

λ,s

(k)=P

∗

= k} =

(λs)

k !

−λs

,k=0, 1, 2, ··· . (2.31)

The probability distribution in (2.31) is called a Poisson distribution, in which,

λ>0 is the strength of the Poisson ﬂow.

2.2 Stochastic Models of Flow Raised by Sequence Mutations 41

Properties of Poisson Flows

1. The mean and variance of a Poisson ﬂow are deﬁned as follows:

⎧

⎪

⎨

⎪

⎩

E{v

∗

} =

∞



k=0

(k)=λs ,

D{v

∗

} = E{(v

∗

− λ)

} =

∞



k=0

(k − λ)

(k)=λs .

(2.32)

2. In the interval (0,s), the probability that Poisson ﬂow will happen at least

once following from (2.31) is computed as follows:



(s)=P

∗

=0} =e

−λs

(s)=P

∗

=1} =(λs)e

−λs

(2.33)

Therefore, this probability distribution obeys an exponential distribution.

3. If v

∗

j,s

, j =1, 2, ···,k are k independent Poisson ﬂows, the mixed Poisson

ﬂow is deﬁned as follows:

∗



j=1

∗

j,s

,s≤ 0 . (2.34)

This is the total number of times that k Poisson ﬂows happen in the

interval (0,s). v

∗

is then also a Poisson ﬂow with the strength parameter

λ =



j=1

Dual Renewal Process of Poisson Flows

Poisson ﬂow is a kind of renewal process and its dual renewal process is deﬁned

∗

=sup{t: v

∗

(t) ≤ k} . (2.35)

∗

is then the random variable for position renewal, that is, the random vari-

able describing the mutation at the kth position. It follows from (2.35) that

the stochastic sequence

∗

= {t

∗

, ···} (2.36)

is a homogeneous and independently incremental process.



∗

=(

∗

,

∗

,

∗

, ···)

is then an independently and identically distributed process and each 

∗

obeys

an exponential distribution, in which 

∗

= t

∗

− t

∗

k−1

{

∗

≤ t} =1− e

λt

,λ,t>0 . (2.37)

Here t

∗



j=1



∗

.Consequently,

∗

is the renewal process of



∗

Each one of the two processes ˜v

∗

and

∗

is the dual renewal process of the

other one, determined by (2.26) and (2.30) if we replace j

∗

by t

∗

in the corres-

ponding formula. For this reason, we can get three alternative representations

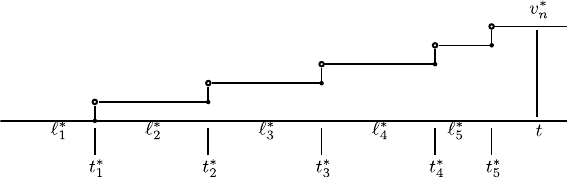
42 2 Stochastic Models of Mutations and Structural Analysis

Fig. 2.2. The sample track function for a Poisson process

of Poisson ﬂow: ˜v

∗



∗

, in which the random variable v

∗

(t)of˜v

∗

means the

time of mutation happening in the position region (0,t). The random variable

∗

refers to the position of the kth mutation and the random variable 

∗

denotes the period between the (k − 1)th and the kth mutations.

The relationships among the three sequences ˜v

∗



∗

are illustrated in

Fig. 2.2.

From Fig. 2.2, we deduce that the sample track function of the Poisson

process is similar to the counting process. Its properties are as follows:

1. v = v

, s ≥ 0 is a jumping and increasing step function with continuous

time and discrete values. It is left continuous. That is, lim

t→s

−

= v

always holds. The left continuous points are denoted by solid dots and

the points that are not within the range of the function are denoted as

voids.

2. Following from the sparseness property of the Poisson process, the heights

at all jump points of the sample track function are at most 1.

3. Let {s

, ···} be a set of jump points arranged in order, then ˜s =

, ···) is called the renewal sequence of the function ˜v. Generally,

the renewal sequence satisﬁes the following condition:

− v

t−



0 , if s does belong to set {s

, ···} ,

1 , if s ∈{s

, ···} ,

(2.38)

in which

t−

= lim



↑s

−



= lim



↓s



4. In Poisson ﬂow ˜v

∗

, the probability of all of these samples ˜v satisfying

the following conditions is 1: (a) 0 ≤ s

< ··· holds and (b)

→∞if k →∞.

The Relationship Between the Bernoulli Process

and the Poisson Process

We have mentioned that the Bernoulli process and the Poisson process can

both describe the mutation of sequences. Now, we further explain their prop-

erties and relationships as follows:

2.2 Stochastic Models of Flow Raised by Sequence Mutations 43

1. The Bernoulli process

ζ applies to discrete stochastic sequences and each

component ζ

=1, 0 designates whether or not a mutation happened at

position i. Thus, it is easy to understand it intuitively.

2. The crucial disadvantage of the Bernoulli process is that the probability

of its counting sequence η



i=1

is diﬃcult to compute directly if n

is too large, because in the binomial distribution b(n, k; ), C

k!(n−k)!

and 

, and we are unable to calculate it exactly for large numbers. As

a result, Poisson ﬂow is typically used to approximate Bernoulli processes.

3. When Poisson ﬂow is used to approximate counting sequences, the chang-

ing of positions becomes continuous. A region is chosen with proper

length n

as its unit. The position n can be replaced by t =

.Thus,the

discrete position region {1, 2, 3, ···} becomes a continuous region (0, ∞).

If n

 = λ,thenn = λt and the binomial distribution

b(n, k; )=C



(1 − )

n−k

∼ p

λt

(k)=

(λt)

−λt

approximates the probability of the Poisson ﬂow. This describes the prob-

ability of the number of times mutation occured in the integer region [1,n],

or a continuous interval (0,t).

2.2.3 Mutated Flows Resulting from the Four Mutation Types

The four types of mutation in biological sequences are deﬁned in Sect. 1.2.1.

Consequently, there are four types of mutated ﬂows corresponding to the four

mutation types. All four types of mutated ﬂows can be denoted by Bernoulli

processes and Poisson processes.

Representation Using Bernoulli Processes

If we use a Bernoulli process

=(ζ

τ,1

,ζ

τ,2

,ζ

τ,3

, ···) ,τ=1, 2, 3, 4 , (2.39)

to represent the mutated ﬂow, then

is also a Bernoulli process for each

τ =1, 2, 3, 4. ζ

τ,j

denotes the random variable that represents whether or not

the mutation type τ happened at position j.Let

denote the strength of the

mutation type τ,then

{ζ

τ,j

=1} = 

{ζ

τ,j

=0} =1− 

. (2.40)

Based on many calculations, we know that 

,

 1and

< 1/2within

the homologous sequence family. Following from

, τ =1, 2, 3, 4, we may

write the corresponding renewal process as follows:

∗

τ,n



j=1

τ,j

,τ=1, 2, 3, 4 , (2.41)

44 2 Stochastic Models of Mutations and Structural Analysis

and

∗

(k)=sup{j : v

∗

τ,j

≤ k},τ=1, 2, 3, 4 . (2.42)

Then {

, ˜v

∗



∗

} are the four equivalent representations of the mutation

type τ,inwhich



∗

τ,k

= j

∗

τ,k

− j

∗

τ,k−1

,k=1, 2, 3, ··· . (2.43)

For each ﬁxed τ =1, 2, 3, 4, the four

, ˜v

∗



∗

are determined according

to the relationships given in Sect. 2.1.

Representation Using Poisson Flow

The four diﬀerent types of mutation ﬂows resulting from the four mutation

types can also be represented using Poisson ﬂow,

˜v

∗

= {v

∗

(t),t≥ 0},τ=1, 2, 3, 4 , (2.44)

and the corresponding strength of the Poisson ﬂow is denoted by λ

For a ﬁxed Poisson ﬂow ˜v

∗

resulting from type τ mutation, we denote its

dual process by

∗

,inwhich

∗

τ,k

=sup{t: v

∗

(t) ≤ k},τ=1, 2, 3, 4 . (2.45)

With arguments similar to those used in Sect. 2.1, we ﬁnd that ˜v

∗

and

∗

are mutually determined for a ﬁxed τ , and satisfy the relationships given in

Sect. 2.1.

Synthesis of Mutation Sequences

Based on the four kinds of mutated processes, we can have an addition of mu-

tations if we assume that the four types of mutations happen independently.

If we let ˜v

∗

, τ =1, 2, 3, 4 denote Poisson ﬂow resulting from the four mutation

types, their sum is deﬁned as follows:

˜v

∗



τ =1

˜v

∗





τ =1

∗

τ,1



τ =1

∗

τ,2



τ =1

∗

τ,3

, ···



. (2.46)

The term ˜v

∗

represents the mutated ﬂow resulting from the four mutation

types happening within the same sequences. Following the properties of Pois-

son ﬂow, we have:

1. ˜v

∗

= {v

∗

(t),t≥ 0} is also a Poisson ﬂow, in which v

∗

(t) is the total

number of times the four types of mutation happen in the region (0,t)

altogether.

2. The strength of the Poisson ﬂow ˜v

∗

is λ

= λ

+ λ

3. Dual process of the Poisson ﬂow ˜v

∗

. They are determined by each

other, and satisfy the relationships given in Sect. 2.1.

2.3 Stochastic Models of Type-I Mutated Sequences 45

2.3 Stoch astic Models of Type-I Mutated Sequences

In the last section, we introduced the four types of mutated ﬂows resulting

from the corresponding four mutation types. Based on these mutated ﬂows,

we now discuss how to obtain the stochastic models for these mutated ﬂows.

Since the eﬀects of the four mutated ﬂows are diﬀerent, we analyze these mu-

tation types in detail and give the stochastic models of the mutated sequences

resulting from each of these mutation types.

2.3.1 Description of Type-I Mutation

The type-I mutation of a sequence is deﬁned in Sect. 1.2.1, which is the ﬁrst

kind of mutation. In comparison, a sequence ˜η mutated from a sequence

resulting from a type-I mutation is simply called the type-I mutated sequence

(of

ξ) in the following text. Although the wording of these two terms is sim-

ilar (type-I mutation and type-I mutated sequence), their meanings are very

diﬀerent. We will discuss how to describe type-I mutated sequences and the

corresponding data structure in this subsection. Let

ξ, ˜η be two stochastic

sequences deﬁned on V

as given in (2.1). Let

(

ξ, ˜η)=((ξ

,η

), (ξ

,η

), (ξ

,η

), ···) (2.47)

be a two-dimensional sequence, in which ξ

,η

∈ V

. This practice problem

requires mention of the fact that ˜η is the sequence (mutated from the se-

quence

ξ) resulting from type-I mutation. For simplicity, ˜η is called the type-I

mutated sequence of

ξ in the following text. To construct the stochastic models

of (

ξ, ˜η), we must make the following two assumptions:

I-1 For the two-dimensional sequence (

ξ, ˜η), (ξ

,η

), j =1, 2, 3, ··· is an i.i.d.

sequence of two-dimensional random vectors, in which

ξ is a perfectly

stochastic sequence.

I-2 For any j =1, 2, 3, ···, the joint probability distribution of the two-

dimensional random vector (ξ

,η

) satisﬁes the following condition:

{(ξ

,η

)=(a, b)} =

⎧

⎨

⎩

1 − 

, if a = b,



, otherwise ,

(2.48)

in which 

is the strength of the type-I mutation.

If a two-dimensional sequence (

ξ, ˜η) deﬁned by (2.47) satisﬁes conditions I-1

and I-2,then˜η represents the standard type-I mutated sequence of

ξ.

Theorem 4.

1. If there is a stochastic sequence

ϑ =(ϑ

,ϑ

, ···) which satisﬁes the

following conditions:

46 2 Stochastic Models of Mutations and Structural Analysis

I-3

ϑ is an independently and identically distributed sequence and it is

independent of

ξ.

I-4 The probability distribution of each ϑ

is deﬁned as

{ϑ

= a} =



1 − 

, if a =0,



, otherwise ,

(2.49)

then (

ξ, ˜η) satisﬁes the conditions I-1 and I-2, in which sequence

= ξ

+ ϑ

, j =1, 2, 3, ···.

2. If a two-dimensional sequence (

ξ, ˜η) satisﬁes conditions I-1 and I-2,then

there is a stochastic sequence

ϑ satisfying the conditions I-3 and I-4 such

that ˜η =

ξ +

ϑ holds and ˜η is a perfectly stochastic sequence.

Proof. We prove this theorem in several steps:

1. We ﬁrst prove proposition 1 of the theorem. If the sequence

ϑ satisﬁes

conditions I-3 and I-4 and ˜η =

ξ +

ϑ,then(ξ

,η

), j =1, 2, 3, ··· is an

independently and identically distributed sequence and

{(ξ

,η

)=(a, b)} = P

{ξ

= a}P

{η

= b|ξ

= a}

{ϑ

= b − a} =

⎧

⎨

⎩

1 − 

, if b = a,



, otherwise .

Consequently, (2.48) holds, and proposition 1 of the theorem is proved.

2. If (

ξ, ˜η) satisﬁes conditions I-1 and I-2,thenweprovethat˜η is a per-

fectly stochastic sequence. Alternatively, we prove that η

is a uniform

distribution, such that

{η

= b} =



a∈V

{(ξ

,η

)=(a, b)}

= P

{(ξ

,η

)=(b, b)} +



a=b

{(ξ

,η

)=(a, b)}

1 − 



a=b



1 − 



Thus, we have proved that η

is a perfectly stochastic sequence.

3. If (

ξ, ˜η) satisﬁes conditions I-1 and I-2 then we prove that there is

a stochastic sequence

ϑ satisfying I-3 and I-4 such that ˜η =

ξ +

ϑ holds.

Let ϑ

= η

− ξ

, j =1, 2, 3, ···; then following from condition I-1,we

have that

ϑ is an i.i.d. sequence. Thus, we need only prove that (2.49)

holds. In fact,

{ϑ

= c} = P

{η

− ξ

= c} =



b−a=c

{(ξ

,η

)=(a, b)}



a∈V

{(ξ

,η

)=(a, c + a)} =



1 − 

if c =0,



, otherwise .