Shen S., Tuszynski J.A. Theory and Mathematical Methods for Bioformatics
Подождите немного. Документ загружается.


2.3 Stochastic Models of Type-I Mutated Sequences 47
That is, (2.49) holds, and the proposition 2 holds. This completes the
proof of the theorem.
Theorem 5. Asequence
˜
ϑ given in Theorem 4 can be decomposed as follows:
ϑ
j
= ζ
j
· ϑ
j
,j=1, 2, 3, ··· , (2.50)
with two components satisfying the following conditions:
I-5
˜
ζ,
˜
ϑ
are two i.i.d. sequences, and
˜
ζ and
˜
ϑ
are independent of each other.
Furthermore, both
˜
ζ and
˜
ϑ
are independent of
˜
ξ.
I-6
˜
ζ is a Bernoulli process with strength
1
, and the probability distribution
of
˜
ϑ
is:
P
r
ϑ
j
= a
=
⎧
⎨
⎩
0 , if a =0,
1
3
, otherwise .
(2.51)
(
˜
ξ, ˜η) then satisfies the conditions I-1 and I-2 if and only if there are two
stochastic sequences
˜
ζ and
˜
ϑ satisfying conditions I-5 and I-6 and which sat-
isfy the following:
η
j
= ξ
j
+ ζ
j
ϑ
j
,j=1, 2, 3, ··· . (2.52)
Definition 9. In (2.52), sequence
¯
ζ represents type-I mutated flow, and the
sequence
˜
ϑ
represents random additive noise (or random interference).
In conclusion, a type-I mutated sequence can be decomposed into the sum
of a Bernoulli process and the product of a Bernoulli process and a random
noise term. We denote the model by
E
∗
1
=
˜
ξ,
˜
ζ
1
,
˜
ϑ
1
, ˜η
, (2.53)
in which
˜
ξ,
˜
ζ
1
,
˜
ϑ
1
are three independently stochastic sequences. Any one of
the three stochastic sequences is i.i.d., and the three common probability
distributions are the uniform distribution, the Bernoulli distribution and the
distribution given in (2.51). The mutated sequence is then determined by
(2.52).
2.3.2 Properties of Type-I Mutations
Reversibility of the Type-I Mutated Sequence
The so-called reversibility of the sequence is the fact that ˜η can be mutated
inversely to
˜
ξ by type-I mutation if ˜η is the type-I mutated sequence of
˜
ξ.
Theorem 6. Under type-I mutation, if ˜η is the mutated sequence of
˜
ξ with
strength
1
,then
˜
ξ is also the mutated sequence of ˜η with strength
1
.

48 2 Stochastic Models of Mutations and Structural Analysis
Proof. For the theorem, we need only prove that sequence
˜
ϑ and sequence ˜η
are independent. To do this, we consider
P
r
{(η
j
,ϑ
j
)=(b, c)} =
a∈V
4
P
r
{(ξ
j
,η
j
,ϑ
j
)=(a, b, c)}
a∈V
4
P
r
{(ξ
j
ϑ
j
)=(a, c)}P
r
{η
j
= b|(ξ
j
,ϑ
j
)=(a, c)} .
Since η
j
= ξ
j
+ ϑ
j
,wehave
P
r
{η
j
= b|(ξ
j
,ϑ
j
)=(a, c)} =
1 , if b = a + c,
0 , otherwise ,
and
P
r
{(η
j
,ϑ
j
)=(b, c)} = P
r
{(ξ
j
ϑ
j
)=(b − c, c)}
=
1
4
P
r
{ϑ
j
c} = P
r
{η = b}P
r
{ϑ
j
= c} , (2.54)
in which the last two equations hold due to the fact that ξ
j
,η
j
both have
uniform distributions on V
4
.
Following from (2.54), we have that η
j
,ϑ
j
are two independent random
sequences. From the independently and identically distributed property of
(ξ
j
,η
j
,ϑ
j
), j =1, 2, 3, ···, we show the independence between ˜η and
˜
ϑ.There-
fore,
˜
ξ =˜η −
˜
ϑ holds. That is,
˜
ξ is the standard type-I mutated sequence of ˜η
with strength
1
. The theorem is therefore proved.
Local Penalty Function of Type-I Mutated Sequences
Here, we discuss the local penalty function for a type-I mutated sequence. Let
(
˜
ξ, ˜η) be a two-dimensional sequence which satisfies conditions I-1 and I-2,
and is therefore independent (definition in Sect. 2.1.2). If w(a, b), a, b ∈ V
4
is
a strongly symmetric penalty function on V
4
, we have the following properties:
1. The mean of w(ξ
i
,η
j
)satisfies
w
i,j
= E{ w(ξ
i
,η
j
)} =
⎧
⎪
⎨
⎪
⎩
1
w
3
, if i = j,
w
4
, otherwise ,
(2.55)
in which w
= w(0, 1) + w(0, 2) + w(0, 3). When i = j,wehave
E{w(ξ
i
,η
j
)} =
a,b∈V
4
w(a, b)P
r
{(ξ
i
,η
j
)=(a, b)}
=
a=b∈V
4
w(a, b)P
r
{(ξ
i
,η
i
)=(a, b)}
=
1
12
a=b∈V
4
w(a, b)=
1
3
3
b=1
w(0,b)=
w
1
4
,

2.3 Stochastic Models of Type-I Mutated Sequences 49
and when i = j,wehave
E{w(ξ
i
,η
j
)} =
a=b∈V
4
w(a, b)P
r
{(ξ
i
,η
j
)=(a, b)}
=
1
16
a=b∈V
4
w(a, b)=
1
4
3
b=1
w(0,b)=
w
3
.
It follows that (2.55) holds.
2. The variance σ
i,j
= D{w(a
∗
i+k
,b
∗
j+k
)} of w(ξ
i
,η
j
), where
σ
i,j
=
a,b∈V
4
[w(a, b) − w
i,j
]
2
P
r
{(ξ
i
,η
j
)=(a, b)} . (2.56)
For any fixed (i, j), we calculate the value of σ
i,j
as follows:
σ
i,j
=
a,b∈V
4
[w(a, b) − w
i,j
]
2
P
r
{(ξ
i
,η
j
)=(a, b)}
=
a,b∈V
4
w
2
(a, b) − w
2
i,j
P
r
{(ξ
ij
,η
j
)=(a, b)}
=
a=b∈V
4
w
2
(a, b)P
r
{(ξ
i
,η
j
)=(a, b)}−w
2
i,j
, (2.57)
in which
w
2
i,j
=
⎧
⎪
⎪
⎨
⎪
⎪
⎩
w
1
3
2
, if i = j,
w
4
2
, otherwise ,
and
a,b∈V
4
w
2
(a, b)P
r
{(ξ
i
,η
j
)=(a, b)} =
⎧
⎪
⎨
⎪
⎩
w
1
3
, if i = j,
w
4
, otherwise ,
and w
= w(0, 1)
2
+ w(0, 2)
2
+ w(0, 3)
2
.Thus,wehave
σ
i,j
=
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
w
1
3
−
w
1
3
2
=
1
3
!
w
−
(w
)
2
1
3
"
, if i = j,
w
4
−
w
4
2
=
1
4
#
w
−
w
2
2
$
, otherwise .
(2.58)
Example 4. If w(a, b)=d
H
(a, b) is the Hamming matrix, we have w
=
w
= 3. Therefore, we have
w
i,j
=
⎧
⎨
⎩
1
, if i = j,
3
4
, otherwise ,
σ
i,j
=
⎧
⎨
⎩
1
(1 −
1
) , if i = j,
3
16
, otherwise .
(2.59)

50 2 Stochastic Models of Mutations and Structural Analysis
3. If w(a, b)=d
WT
(a, b) is the WT-matrix, we can see that: w
=1.99,
w
=1.3883, then we have
w
i,j
=
0.66 ×
1
, if i = j,
0.4975 , otherwise ,
σ
i,j
=
1
(0.4711 − 0.044 ×
1
) , if i = j,
0.1058 , otherwise .
(2.60)
Using the calculation in Example 4, we obtain an overall impression of
the local penalty function for a type-I mutated sequence.
Limit Properties of the Local Penalty Function of a Type-I
Mutated Sequence
Following from Theorems 3 and 4, we obtain the limit properties of the local
penalty function of a type-I mutated sequence.
Theorem 7. If ˜η is a type-I mutated sequence of
˜
ξ satisfying conditions I-1
and I-2,andifW is a strongly symmetric matrix, then the limit properties of
the local penalty function of
˜
ξ, ˜η are as follows:
1. As n →∞, the limitation
w(
˜
ξ, ˜η; i, j, n)=
1
n
n
k=1
w(ξ
i+k
,η
j+k
) → w
i,j
a.e. (2.61)
in which w
i,j
is computed by (2.55).
2. The central limit theorem: if n is large enough,
1
σ
ij
√
n
n
k=1
[w(ξ
i+k
,η
j+k
) − μ
ij
] ∼ N (0, 1) , (2.62)
in which σ
i,j
is given by (2.58). The results of (2.61) and (2.62) follow
from the Kolmogorov law of large numbers and the Levy–Lindberg central
limit theorem.
2.4 Type-II Mutated Sequences
We continue to discuss stochastic models for type-II, type-III, and type-IV
mutations. The description for these is similar to queuing theory – where we
consider a service station and the customers arriving as a representation of
the mutation flow. The time each customer spends at the station is analogous
to the lengths resulting from type-II, type-III, and type-IV mutations. In this
subsection, we consider the models that arise from type-II mutations.
2.4 Type-II Mutated Sequences 51
2.4.1 Description of Type-II Mutated Sequences
A type-II mutation (defined in Sect. 1.2) refers to the permutation of some
segments of a biological sequence A =(a
1
,a
2
, ··· ,a
N
). For example,
A = (00201[332]0110203[01022]23101011[20]3321) ,
B = (00201[20]0110203[332]23101011[01022]3321) .
(2.63)
Then, in sequence A the data [332], [01022], [20] in the square brackets permute
and turn into the segments [20], [332], [01022] of sequence B. Data permutation
on more disconnected segments is very important in gene or protein analysis.
In recent years, bioinformatics has begun to solve these problems. We do not,
however, intend to address the subject in this book due to its complexity.
In this book, we confine our discussion to simpler cases. That is, we only
discuss data permutation of two coterminous segments. For example,
A = (00201{[332][0110](00201{[332][0110]}20301022231{[01011][20]}3321) ,
B = (00201{[0110][332]}20301022231{ [20][01011]}3321) .
(2.64)
The sequence B results from the permutation of the data segments in large
brackets {[332][0110]}, {[01011][20]} of sequence A.Afterthis,thenewseg-
ments of sequence B are {[0110][332]}, {[20][01011]}, in which each large
bracket contains the permutation of two coterminous segments.
2.4.2 Stochastic Models of Type-II Mutated Sequences
The following assumptions are required in order to build models of type-II
mutated sequences:
II-1 The mutation sequence ˜η is determined by a stochastic sequence
˜
ξ,
˜
ζ
2
,
and (
˜
∗
1
,
˜
∗
2
). The explanation is as follows:
1.
˜
ξ is a perfectly stochastic sequence on V
4
. It is an initial sequence
to be mutated.
2.
˜
ζ
2
is a Bernoulli process with strength
2
. It is similar to the se-
quence defined in (2.38), to describe whether or not type-II muta-
tion happens.
3. (
˜
∗
1
,
˜
∗
2
) is a stochastic sequence to describe the permutation length
of the type-II mutation, in which
˜
∗
τ
=(
∗
τ,1
,
∗
τ,2
,
∗
τ,3
, ···) ,τ=1, 2 , (2.65)
are two independently and identically distributed stochastic se-
quences and each
∗
τ,j
obeys a geometric distribution:
P
r
{
∗
τ,j
= k} = e
p
τ
(k)=p
τ
(1 − p
τ
)
k−1
,τ=1, 2 . (2.66)
52 2 Stochastic Models of Mutations and Structural Analysis
Here, (
∗
1,j
,
∗
2,j
) represent two segments with lengths
∗
1,j
,
∗
2,j
per-
mutated after the jth mutation. Thus, (
˜
∗
1
,
˜
∗
2
) is the length sequence
of the permutated segments in type-II mutation.
II-2 Suppose
˜
ξ,
˜
ζ
2
,
˜
∗
1
,
˜
∗
2
are four independent stochastic sequences. Let
˜a, ˜z,
˜
1
,
˜
2
denote the samples of the stochastic sequences
˜
ξ,
˜
ζ
2
,
˜
∗
1
,
˜
∗
2
in which
⎧
⎪
⎨
⎪
⎩
˜a =(a
1
,a
2
,a
3
, ···) ,
˜z =(z
1
,z
2
,z
3
, ···) ,
˜
τ
=(
τ ;1
,
τ ;2
,
τ ;3
, ···) ,τ=1, 2 .
(2.67)
The construction of the type-II mutated sequence ˜η produced by
(˜a, ˜z,
˜
1
,
˜
2
) is then as follows:
1. The renewal processes ˜v
∗
2
and
˜
j
∗
2
are caused by
˜
ζ
2
.
v
∗
2,n
=
n
j=1
ζ
2,j
,j
∗
2,k
=sup{n: v
∗
2,n
<k} , (2.68)
and their samples are respectively
˜v
2
=(v
2,0
,v
2,1
,v
2,2
, ···) ,
˜
j
2
=(j
2,0
,j
2,1
,j
2,2
, ···) ,
(2.69)
in which v
2,n
denotes the time of the type-II mutation in position
region { 1, 2, ···,n}. j
2,k
denotes the kth position occurrence of the
type-II mutation, in which v
2,0
= j
2,0
=0.˜v
∗
2
,
˜
j
∗
2
are then deter-
mined by
˜
ζ
2
.Consequently,˜v
2
,
˜
j
2
are determined by ˜z
2
.
2. If ˜a,
˜
j
2
,
˜
1
,
˜
2
are similar to that given in (2.67) and (2.69), then
sequence ˜a can be decomposed into several regions as follows:
⎧
⎪
⎨
⎪
⎩
δ
2,0;k
=[j
2,k−1
+
1,k−1
+
2,k−1
+1,j
2,k
] ,
δ
2,1;k
=[j
2,k
+1,j
2,k
+
1,k
] ,
δ
2,2;k
=[j
2,k
+
1,k
+1,j
2,k
+
1,k
+
2,k
] ,
(2.70)
in which k =1, 2, 3, ···,[i, j]={i, i +1, ···,j} is the set of positive
integers. [i, j]=Φ if i>j,andj
2,0
=
1,0
=
2,0
=0.
Formula (2.70) divides a long sequence V
+
=(1, 2, 3, ···)intosev-
eral regions as follows:
V
+
=(δ
2,0,1
,δ
2,1,1
,δ
2,2,1
,δ
2,0,2
,δ
2,1,2
,δ
2,2,2
, ··· ,
δ
2,0,k
,δ
2,1,k
,δ
2,2,k
, ···) . (2.71)
Then Δ
2,0
,Δ
2,1
,Δ
2,2
represent the non-type-II mutation region
and type-II region mutation respectively, in which
⎧
⎪
⎨
⎪
⎩
Δ
2,0
=(δ
2,0;1
,δ
2,0;2
,δ
2,0;3
, ···) ,
Δ
2,1
=(δ
2,1;1
,δ
2,1;2
,δ
2,1;3
, ···) ,
Δ
2,2
=(δ
2,2;1
,δ
2,2;2
,δ
2,2;3
, ···) .
(2.72)
2.4 Type-II Mutated Sequences 53
Equations (2.71) and (2.72) refer to the region structure of type-II
mutated positions. The region in the region structure of type-II mu-
tated positions is also random if
˜
ζ
2
,
˜
1
,
˜
2
are stochastic sequences.
Hence, (2.70) becomes
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
δ
∗
2,0;k
=
j
∗
2,k−1
+
∗
1,k−1
+
∗
2,k−1
+1,j
∗
2,k
,
δ
∗
2,1;k
=
j
∗
2,k
+1,j
∗
2,k
+
∗
1,k
,
δ
∗
2,2;k
=
j
∗
2,k
+
∗
1,k
+1,j
∗
2,k
+
∗
1,k
+
∗
2,k
.
(2.73)
Correspondingly, (2.71) and (2.72) become stochastic regions, such
that
V
+
=(δ
∗
2,0;1
,δ
∗
2,1;1
,δ
∗
2,2;1
,δ
∗
2,0;2
,δ
∗
2,1;2
,δ
∗
2,2;2
, ···) .
Similarly,
Δ
∗
2,τ
=(δ
∗
2,τ;1
,δ
∗
2,τ;2
,δ
∗
2,τ;3
, ···) ,τ=0, 1, 2 .
Consequently, these random variables satisfy the relationships
j
∗
2,k−1
<j
∗
2,k
,
∗
τ,k
> 0 for any τ =1, 2,k=1, 2, 3, ···.
3. Let
˜
b =(b
1
,b
2
,b
3
, ···), b
j
∈ V
4
denote the samples of ˜η,sothat
˜
b is
determined by the following steps:
(a) If j ∈ Δ
2,0
,thenj is the position in the non-type-II mutated
region and b
j
= a
j
holds. This means the data are invariant.
(b) If j ∈ Δ
2,1
∪Δ
2,2
,thenj is the position in the type-II mutated
region and the data segments in δ
2,1
and δ
2,2
are permutated.
Let the kth segment of Δ
2,1
and Δ
2,2
be
δ
2,1;k
= {j
k
+1,j
k
+2, ··· ,j
k
+
1;k
},
δ
2,2;k
= {j
k
+
1;k
+1,j
k
+
1;k
+2, ··· ,j
k
+
1;k
+
2;k
} .
(2.74)
Then the permutated data of the kth type-II mutation is
b
δ
2,0;k
= a
δ
2,0,k
, (b
δ
2,1,k
,b
δ
2,2,k
)=(a
δ
2,2,k
,a
δ
2,1,k
) , (2.75)
the notations of which are defined in (1.13) and (1.14).
4. Following from the above discussions, we will obtain the type-II
mutated sequence ˜η defined by
˜
ξ,
˜
ζ
2
,
˜
1
,
˜
2
. Hence, let
E
∗
2
=
˜
ξ,
˜
ζ
2
,
˜
∗
1
,
˜
∗
2
, ˜η
(2.76)
be the stochastic model of the type-II mutated sequence, in which
each stochastic sequence satisfies conditions II-1 and II-2 and the
supplemental explanations. From (2.75), the type-II mutated se-
quence ˜η can be determined.
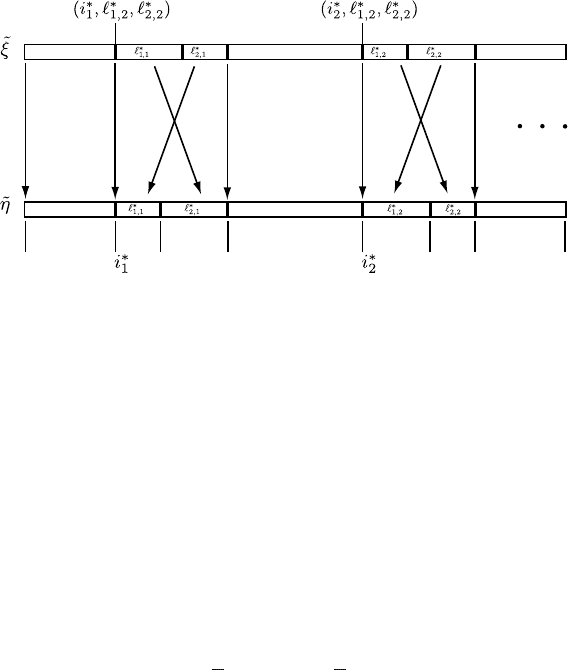
54 2 Stochastic Models of Mutations and Structural Analysis
Fig. 2.3. Relationships of type-II mutations
Relationships of the type-II mutated sequences are shown in Fig. 2.3.
In Fig. 2.3, ˜η is a type-II mutated sequence of
˜
ξ,inwhich,i
∗
k
is the kth type-
II mutated position and
∗
1,k
,
∗
2,k
are the lengths of the permutated segments
of the kth type-II mutations.
2.4.3 Error Analysis of Type-II Mutated Sequences
The error analysis of type-II mutated sequences indicates the calculation of
penalty scores resulting from comparing a mutated sequence with the initial
sequence. If ˜η is a type-II mutated sequence of
˜
ξ, then the definition of the
local penalty function is the same as (2.55). Similarly, let
w
˜
ξ, ˜η; i, j, n
=
1
n
w
¯
ξ
i
, ¯η
j
=
1
n
n
k=1
w(ξ
i+k
,η
j+k
) . (2.77)
We then discuss how to calculate or estimate the penalty scores.
Estimating the Lengths of Permutated Segments
of Type-II Mutated Sequences
To estimate the value of (2.77), we need to estimate the total length of the
permutated segments in the type-II mutated sequences. We begin by estimat-
ing the length of the permutated segment of type-II mutated sequences at the
kth position.
1. Denote the length of the permutated segment at the kth position by
∗
0,k
=
∗
1,k
+
∗
2,k
. Following from the i.i.d. property of
˜
∗
τ
, τ =1, 2 individually,
and the independence between the two sequences, we have that
˜
∗
0
= {
∗
0,1
,
∗
0,2
,
∗
0,3
, ···}
2.4 Type-II Mutated Sequences 55
is an independent and identically distributed sequence, and the common
probability distribution of
∗
0,k
can be calculated as follows:
P
r
{
∗
0,k
= } = P
r
{
∗
1,k
+
∗
2,k
= }
=
−1
=1
P
r
{
∗
1,k
=
}P
r
{
∗
2,k
= −
}
=
−1
=1
p
1
(1 − p
1
)
−1
p
2
(1 − p
2
)
−
−1
=
p
1
p
2
(1 − p
1
)(1 − p
2
)
−1
=1
(1 − p
1
)
(1 − p
2
)
−
.
When p
1
= p
2
we have
P
r
{
∗
2,j
= } =
p
1
p
2
(1 − p
2
)
(1 − p
1
)(1 − p
2
)
−1
=1
1 − p
1
1 − p
2
=
p
1
p
2
(1 − p
2
)
−1
1 − p
2
⎛
⎜
⎝
1 −
1−p
1
1−p
2
−1
1 −
1−p
1
1−p
2
⎞
⎟
⎠
= p
1
p
2
(1 − p
2
)
−1
− (1 − p
1
)
−1
p
1
− p
2
. (2.78)
If p
1
= p
2
= p, then (2.78) can be simplified as
P
r
{
∗
2,j
= } =( − 1)p
2
(1 − p)
−2
,=2, 3, 4, ··· . (2.79)
For simplicity, the probability distribution of
∗
0,k
is denoted by p
0
()=
P
r
{
∗
0,k
= }.
Based on the expectation value formula and the variance of geometric
distribution given, we calculate the mean and variance of
∗
2,j
as follows:
⎧
⎪
⎨
⎪
⎩
E{
∗
0,k
} = E{
∗
1,k
} + E{
∗
2,k
} =
1
p
1
+
1
p
2
,
D{
∗
0,k
} = D{
∗
1,k
} + D{
∗
2,k
} =
1 − p
1
p
2
1
+
1 − p
2
p
2
2
.
(2.80)
2. Following from the definition of E
∗
2
, we have that the counting process
of type-II mutated sequences from the Bernoulli process
˜
ζ
2
is defined as
follows:
˜v
∗
2,n
=
n
i=1
ζ
2,i
,n=1, 2, 3, ··· .
Then, let
ψ
2,n
=
v
∗
n
k=1
0,k
,n=1, 2, 3, ··· (2.81)
be the compound renewal sequence of
˜
ζ
2
and
˜
∗
0
.
56 2 Stochastic Models of Mutations and Structural Analysis
3. Based on the property of the compound renewal process we can determine
the limit character of the sequence ψ
2,n
.Here
1
n
ψ
2,n
=
1
n
v
∗
n
k=1
ζ
2,k
∼
2
μ
0
, (2.82)
in which μ
0
=
1
p
1
+
1
p
2
, and
E{ψ
2,n
} = E
⎧
⎨
⎩
v
∗
n
k=1
ζ
2,k
⎫
⎬
⎭
= n
2
μ
0
. (2.83)
We can see that the central limit property is given by
1
σ
2
√
n
[ψ
2,n
− n
2
μ
0
]=
1
σ
2
√
n
⎛
⎝
v
∗
n
k=1
ζ
2,k
− n
2
μ
0
⎞
⎠
∼ N (0, 1) , (2.84)
in which
σ
2
2
=
1
n
D{ψ
2,n
} =
2
!
2 −
2
− p
1
p
2
1
+
2 −
2
− p
2
p
2
2
+
2(1 −
2
)
p
1
p
2
"
. (2.85)
Equation (2.85) is obtained by the calculation of ψ
2,n
. We do not present
the derivations here.
Estimation of the Penalty Function w(
˜
ξ, ˜η; i, j, n)
To estimate the penalty function of (2.84), the following must be considered:
1. We first discuss the calculation of w(ξ
i
,η
j
). Here w(a, b) is the penalty
matrix on V
4
which satisfies the strongly symmetric condition.
The values of the type-II mutated sequence η
j
in w(ξ
i
,η
j
)arejustthe
components ξ
k
of
˜
ξ. Therefore,
E{w(ξ
i
,η
j
)} =
0 , if η
j
= ξ
k
,k= i
w
1
, if η
j
= ξ
k
,k= i,
(2.86)
in which w
1
=
1
4
[w(0, 1) + w(0, 2) + w(0, 3)].
2. We estimate the value of w(
˜
ξ, ˜η; i, j, n) for the condition i = j. For uni-
versality, we set i = j = 0, and denote
Δ
∗
2
(n)=(Δ
∗
2,1
∪ Δ
∗
2,2
) ∩ N, (2.87)
in which the definition of Δ
∗
2,1
, Δ
∗
2,2
is in (2.72) and N = {1, 2, ··· ,n}.
Here ||Δ
∗
2
(n)|| = ψ
v
∗
2,n
is established. If i is not in Δ
∗
2
(n), w(ξ
i
,η
i
) ≡ 0
