Shen S., Tuszynski J.A. Theory and Mathematical Methods for Bioformatics
Подождите немного. Документ загружается.

98 3 Modulus Structure Theory
Theorem 18. If the shifting mutation operator T defined by (3.72) satisfies
the basic assumption (3.79), then the operator T
b
= T
−1
a
mutating B to A is
also a shifting mutation operator with the following properties:
1. The number of the shifting mutations from B to A are equal to the number
of the shifting mutations caused by T
a
;hence,k
b
= k
a
.
2. Mutation positions in the sequence B are
i
k
= i
k
+ L
k
,k=1, 2, ··· ,k
a
, (3.80)
where L
k
=
k−1
k
=1
k
is the shifting function induced by the shifting mu-
tation operator T
a
.
3. The i
k
defined by (3.80) is strictly monotonic increasing, that is,
1=i
0
≤ i
1
<i
2
< ···<i
k
a
≤ i
k
a
+1
= n
b
,
where n
b
= n
a
+ L
0,k
a
+1
.
4. The insertion operation of T
b
= T
−1
a
simply corresponds to the deletion
operation of T
a
. In other words, the insertion of T is the deletion of T
−1
,
and the deletion of T is the insertion of T
−1
. It can also be found that
T
−1
a
= {(i
k
, −
k
) ,k=1, 2, ··· ,k
a
} . (3.81)
Proof. The proofs of propositions 1, 2, and 4 in Theorem 18 only involve
the decomposition expression (3.61). In fact, the decomposition expression
(Δ
0
,Δ
1
,Δ
2
)ofN
c
is determined if T
a
is known. We then have (c
Δ
0
,c
Δ
2
)=B,
and obtain C by inserting c
Δ
1
into B. Obviously, this data fragment c
Δ
1
is
just the part deleted from A. On the other hand, to obtain A, we need only
delete the data fragment c
Δ
2
from sequence C. This fragment c
Δ
2
is inserted
into A to find N
c
. Therefore, the mutation from B to A is just the inverse
of the mutation from A to B.Sincec
Δ
1
and c
Δ
2
in C are disjoint, it follows
that T
−1
is a purely shifting mutation, and expressions (3.79) and (3.80) hold.
Thus, the propositions 1, 2, and 4 of Theorem 18 are proved. To prove propo-
sition 3, we involve the conditions of shifting mutations and expression (3.79).
We then have
i
k+1
− i
k
=(i
k+1
+ L
0,k+1
) −(i
k
+ L
0,k
)=i
k+1
− i
k
+
k
> 0 .
Following from the conditions of purely shifting mutations, we have
i
k+1
− i
k
+ |
k
| > 0 for every k =1, 2, ··· ,k
a
. Thus, proposition 3 holds,
and the theorem is proved.
Example 12. In Example 6, the shifting function is
¯
L =(L
0,1
,L
0,2
,L
0,3
,L
0,4
)=(0, 4, 1, −3, −1)
3.4 The Binary Operations of Sequence Mutations 99
and the mutation mode from B to A is
T
−1
= {(7, −4), (17, 3), (21, 4), (26, −2)} .
Next, we let T
b
= T
−1
a
be the inverse of T
a
.Thus,B is completely determined
by B = T
a
(A), if A
= c
Δ
1
is given. However, A is determined by A =
T
−1
(B), if B
= c
Δ
2
= a
Δ
2
is known.
Addition of Operators of Consistent Mutations
Let T
1
,T
2
be two mutation modes based on the initial template A and satis-
fying the consistent condition, and let T
3
= T
2
∨ T
1
. The operators T
1
, T
2
,
T
3
induced by T
1
,T
2
,T
3
are then shifting operators if T
3
satisfies the basic
assumption of shifting mutations. Their mutual relationships are described as
follows:
1. Following from the consistent conditions and the definition of T
3
=
T
2
∨ T
1
,wehavethatT
1
,T
2
≤ T
3
. Therefore, all mutation positions of
A can be uniformly denoted by I
3
= {i
1
,i
2
, ··· ,i
k
a
}, and their modulus
structures can be also uniformly represented by
T
θ
= {(i
k
,
τ
k
) ,k=1, 2, ···,k
a
} ,θ=1, 2, 3 , (3.82)
where
3
k
=
max
1
k
,
2
k
, when
1
k
,
2
> 0 ,
min
1
k
,
2
k
, when
1
k
,
2
< 0 .
2. T
1
,T
2
,T
3
can be decomposed as follows:
T
1
=
T
1
+
,T
1
−
,T
2
=
T
2
+
,T
2
−
,T
3
=
T
3
+
,T
3
−
,
in which T
1
+
,T
2
+
,T
3
+
are the modulus structures induced by type-III mu-
tation, and T
1
−
,T
2
−
,T
3
−
are the modulus structures induced by type-IV
mutation. The uniform expression is given as follows:
T
θ
τ
=
i
θ
τ,k
,
θ
τ,k
,k=1, 2, ··· ,k
θ
τ
,θ=1, 2, 3 ,τ=+, − . (3.83)
3. The operator induced by T
θ
is denoted by T
θ
and defined by
T
θ
(A, E
θ
)=B
θ
,θ=1, 2, 3 , (3.84)
in which E
θ
=(E
θ
1
,E
θ
2
, ··· ,E
θ
k
θ
+
), θ =1, 2, 3 are templates of inserted
data. Since ||E
θ
k
|| =
θ
+
,wehave||E
1
+
||, ||E
2
+
|| ≤ ||E
3
+
||.Asaresult,we
have the following theorem.
Theorem 19. If T
1
and T
2
are two consistent modes based on the template A,
and T
3
= T
2
∨ T
1
satisfies the basic assumption, then the three operators
T
1
, T
2
, T
3
induced by T
1
,T
2
,T
3
are shifting operators and satisfy the prop-
erties as follows:
100 3 Modulus Structure Theory
1. Let E
4
=(E
4
1
,E
4
2
, ··· ,E
4
k
a
),inwhichE
4
k
= E
3
k
− E
1
k
for each k and let
B
1
= T
1
(A, E
1
).IfE
1
k
is a subvector of E
3
k
for each k, then we have
B
3
= T
3
(A, E
3
)=T
2
1
(B
1
,E
4
)=T
2
1
[T
1
(A, E
1
),E
4
] , (3.85)
in which T
2
1
is a shifting operator on B
1
and its modulus structure is
defined as follows:
T
2
1
=
j
k
,
2
k
,k=1, 2, ··· ,k
a
, (3.86)
where
2
k
is defined in (3.82), and j
k
= i
2
k
+ L
1
k
, L
1
k
=
k−1
k
=1
1
k
is the
shifting function of T
1
.
2. If E
1
k
∪E
2
k
= E
3
k
for each k,thenletE
5
k
= E
3
k
−E
2
k
, E
5
=(E
5
1
,E
5
2
, ··· ,E
5
k
a
)
and B
2
= T
2
(A, E
2
), we have
B
3
= T
3
(A, E
3
)=T
1
2
(B
2
,E
5
)=T
2
1
[B
1
,E
4
] , (3.87)
in which T
1
2
is the shifting operator on the sequence B
2
. Its modulus struc-
ture is defined by:
T
1
2
=
j
k
,
1
k
,k=1, 2, ··· ,k
a
, (3.88)
where
1
k
is defined by (3.82), j
k
= i
1
k
+ L
2
k
and L
2
k
=
k−1
k
=1
2
k
is the
shifting function of T
2
. It follows from (3.88) that the multiplication of
shifting operators T
1
and T
2
is commutative.
The proof of this theorem follows from properties 1 and 2 above.
3.5 Error Analysis for Pairwise Alignment
If B is mutated from A,then(A
,B
) is the aligned sequence of (A, B). In
this section, we analyze the error problem. These four sequences A, B, A
,B
transform into the uniform form as follows:
U =(u
1
,u
2
, ··· ,u
n
u
) ,U= A, B, A
,B
,u= a, b, a
,b
,
where n
a
= n
b
and a
i
,b
i
∈ V
q
, a
j
,b
j
∈ V
q+1
,andq ∈ V
q+1
is a virtual
symbol. For simplicity, we still assume q =4.
3.5.1 Uniform Alignment of Mutation Sequences
Definition of the Uniform Alignment of Mutation Sequences
In Sects. 3.2 and 3.3, we mentioned mutation modes for both the sequence
alignment and mutation. If the mutation positions are just the inserting po-
sitions raised by the alignment, then the alignment is a uniform alignment.
The definition is as follows:
Definition 23. Let B be the sequence mutated from A,and(A
,B
) is the
alignment of (A, B).IftheinsertionpartofA
is caused by type-III mutation,
and the insertion part of B
is caused by type-IV mutation acting on A,then
(A
,B
) is the uniform alignment of (A, B).
3.5 Error Analysis for Pairwise Alignment 101
Properties of Uniform Alignment
By Definition 23 we can determine the relationship between the modulus
structure induced by uniform alignment and the modulus structure induced
by mutations:
1. If B is mutated from A, and its mutation mode T
A
is defined by (3.53) or
(3.54), then the mutation mode from B to A is T
b
= T
−1
a
.ModesT
a
and
T
b
can be decomposed as follows:
T
a
=(T
a,+
,T
a,−
) ,T
b
=(T
b,+
,T
b,−
) ,
where T
a,+
,T
b,+
are the modes induced by type-III mutation based on
the initial templates A and B, respectively, and T
a,−
,T
b,−
are modes re-
sulting from type-IV mutation based on the initial templates A and B,
respectively.
2. If (A
,B
) is the uniform alignment of sequence (A, B), the expanded
mode from A to A
is H
a
= T
a,+
, and the expanded mode from B to B
is H
b
= T
b,+
.
3. If B is mutated from A purely by shifting mutations, then the uniform
alignment can be represented using the core D and envelope C,where
C =(c
Δ
0
,c
Δ
1
,c
Δ
2
), D = c
Δ
0
, A =(c
Δ
0
,c
Δ
1
), and B =(c
Δ
0
,c
Δ
2
).
4. If (A
,B
) is the alignment of (A, B) and the following conditions are
satisfied:
a
j
=
c
j
, if j ∈ Δ
0
∪ Δ
1
,
4 , if j ∈ Δ
2
,
b
j
=
c
j
, if j ∈ Δ
0
∪ Δ
2
,
4 , if j ∈ Δ
1
.
(3.89)
Then (A
,B
) is the uniform alignment of (A, B)andn
a
= n
b
= n
c
.
Example 13. In Example 12, the modulus structures of A and B are given as
follows:
T
A
= {(7, 4), (13, −3), (20, −4), (29, 2)},
T
B
= {(7, −4), (17, 3), (21, 4), (26, −2)} .
If (A
,B
) is the uniform alignment of (A, B), it follows that the modulus
structures from A to A
and from B to B
are:
H
a
= T
a,+
= {(7, 4), (29, 2)},H
b
= T
b,+
= {(17, 3), (21, 4)} .
Therefore, we find the representation of the uniform alignment (A
,B
),
A
= (0000000444411111113330000333311111440000) ,
B
= (0000000222211111114440000444411111220000) ,
and the core D and envelope C are
D = (000000011111133300003333111110000) ,
C = (000000022221111113330000433311111220000) .
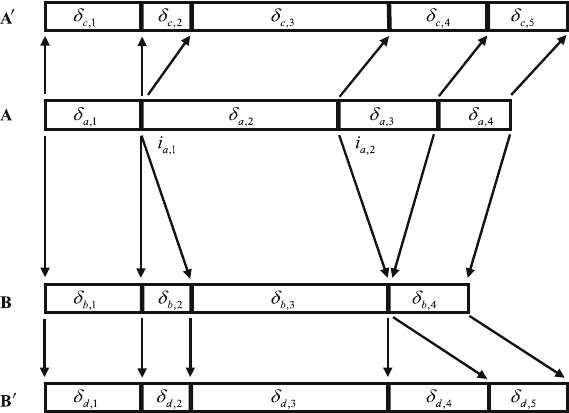
102 3 Modulus Structure Theory
Fig. 3.4. The modulus structure of uniform alignment
The relationship between sequence mutation and uniform alignment is illus-
trated in Fig. 3.4.
In Fig. 3.4, (A
,B
) is the alignment of (A, B), and T =(T
+
,T
−
)isthe
modulus structure, where
T
+
= {i
1
,
1
},T
−
= {i
2
,
2
} .
Thus, the modulus structure of uniform alignment is
H
a
= {i
1
,
1
},H
b
= {i
2
,
2
} ,
with
1
= ||δ
b,2
|| = ||δ
c,2
||,
2
= ||δ
a,3
|| = ||δ
d,4
|| .
3.5.2 Optimal Alignment and Uniform Alignment
The definition of optimal alignment was presented in Chap. 1. In this section,
we study the relationship between optimal alignment and uniform alignment.
A uniform alignment is optimal if
1
1/2. However, this is not generally
the case.
Example 14. We delete segment (23210) from the initial template
A = (11231003221000[23210]3221{}02112003), and insert a segment (11230)
into the large bracket of A between segments (3221) and (0211), and perform
3.5 Error Analysis for Pairwise Alignment 103
type-I and type-II mutations outside the insertion and deletion region. Let
the final output mutated from A be
B = (112310032210003220[11230]12112003) .
Then the uniform alignments of A, C are given as follows:
A
1
= (11231(0)032210(0)0[23210]322(1)[44444](0)2112003) ,
B
1
= (11231(2)032210(1)0[44444]322(0)[11230](1)2112003) ,
where the components in parentheses are caused by type-I and type-II mu-
tations, and components in square brackets are from type-III and type-IV
mutations. The Hamming matrix between them is d
H
(A
,B
) = 14 and the
optimal alignment is
A
0
= (11231(0)032210(0)0[23210]322[4]1[444]0[4]2112003) ,
B
0
= (11231(2)032210(1)0[44444]322[0]1[123]0[1]2112003) ,
where d
H
(C
,D
)=12<d
H
(A
,B
). Therefore, (A
,B
) is the uniform align-
ment of (A, B) but is not an optimal alignment. Making use of Example 8,
we find that a uniform alignment can be represented by a minimum penalty
alignment through a local modification. The local modification permutes the
insertion symbols with their nearest nucleotides. For example, (A
0
,B
0
)isalo-
cal modification of (A
1
,B
1
). The details of local modification will be discussed
later.
It is worth noting that a uniform alignment may not be a minimal penalty
alignment even if
1
=
2
= 0; this corresponds to the cases where type-I and
type-II mutations do not work.
Example 15. If we delete the segment (0000) from the initial template A =
(1212000012121212001212) and insert the segment (121200) into A between
(01212) and (121200), then A and the output B mutated from A are compared
as follows:
A = (1212[0000]12121212001212) ,
B = (12121212[121200]1212001212) .
The uniform alignment is given by:
A
1
= (1212[0000]1212[444444]1212001212) ,
B
1
= (1212[4444]1212[121200]1212001212) .
Therefore d
H
(A
1
,B
1
) = 10, and we can construct a new alignment as follows:
A
0
= (1212[00]001212[4444]1212001212) ,
B
0
= (1212[44]121212[1200]1212001212) .
Hence, d
H
(A
0
,B
0
)=8<d
H
(A
1
,B
1
). It follows that an optimal alignment
(A
,B
) may not be the minimal penalty alignment.

104 3 Modulus Structure Theory
3.5.3 Error Analysis of Uniform Alignment
Let B
∗
be a stochastic sequence mutated from the stochastic sequence A
∗
,
which is determined by expression (2.93). Let (C
∗
,D
∗
) be the uniform align-
ment of (A
∗
,B
∗
). The error analysis of (C
∗
,D
∗
) is then an estimate of the
absolute error
w(C
∗
,D
∗
)=
n
c
∗
j=1
w
c
∗
j
,d
∗
j
. (3.90)
For simplicity, we assume the penalty matrix is the Hamming matrix; i.e.,
w(a, b)=0or1,fora = b or a = b:
1. We can decompose the expression (3.90) as follows:
w(C
∗
,D
∗
)=
j∈Δ
∗
0
w
c
∗
j
,d
∗
j
+
j∈Δ
∗
3
w
c
∗
j
,d
∗
j
+
j∈Δ
∗
2
w
c
∗
j
,d
∗
j
. (3.91)
Since c
∗
j
=4,d
∗
j
= 4 in the second part, and d
∗
j
=4,c
∗
j
=4inthethird
part, it follows that
j∈Δ
∗
3
w
c
∗
j
,d
∗
j
= n
∗
3
,
j∈Δ
∗
2
w
c
∗
j
,d
∗
j
= n
∗
2
.
Therefore, expression (3.91) becomes
w(C
∗
,D
∗
)=
j∈Δ
∗
0
w
c
∗
j
,d
∗
j
+ n
∗
1
+ n
∗
2
, (3.92)
where n
∗
1
and n
∗
2
are the total lengths of the type-III and type-IV muta-
tions respectively. Both are random numbers.
2. The estimate of n
∗
1
and n
∗
2
in the expression (3.92). Since T
∗
= {(i
∗
k
,
∗
k
),
k =1, 2, ··· ,k
∗
a
} is a random modulus structure of random mutation, and
based on the assumptions of type-III and type-IV mutations and the large
number law, we estimate n
∗
1
,n
∗
2
as follows:
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
n
∗
1
=
k:
∗
k
>0
∗
k
∼ n
a
1+
3
p
3
,
n
∗
2
=
k:
∗
k
<0
∗
k
∼ n
a
1+
4
p
4
.
(3.93)
3. To estimate the first term in expression (3.92), we begin with the following
notations:
(a) (c
∗
j
,d
∗
j
)=(a
∗
j
,a
∗
j
+ ζ
j
) for all j ∈ Δ
∗
0
is an i.i.d. sequence. a
∗
j
is
a uniform distribution on V
4
, ζ
j
is defined by (3.96), and
˜
ζ and A
∗
are
3.5 Error Analysis for Pairwise Alignment 105
independent. Therefore,
⎧
⎪
⎨
⎪
⎩
E
w(c
∗
j
,d
∗
j
)
=
a,b∈V
4
p(a, b)w(a, b)=,
D
w(c
∗
j
,d
∗
j
)
=
a,b∈V
4
p(a, b)[w(a, b) − ]
2
=
a,b∈V
4
p(a, b)w
2
(a, b) −
2
= (1 − ) .
(3.94)
(b) For any pair j = j
∈ Δ
0
, the two components of (c
∗
j
,d
∗
j
)=
(a
∗
j
,a
∗
j
+ ζ
j
) are independent and both are uniform distributions on
V
4
, therefore
⎧
⎪
⎨
⎪
⎩
E
w(c
∗
j
,d
∗
j
)
=
a,b∈V
4
p(a)p(b)w(a, b)=3/4 ,
D
w(c
∗
j
,d
∗
j
)
=
a,b∈V
4
p(a, b)[w(a, b) − 3/4]
2
=
a,b∈V
4
p(a, b)w
2
(a, b) − (3/4)
2
=3/16 .
(3.95)
(c) Based on the definition of Δ
∗
0
,wehavethatΔ
∗
0
is composed of several
small intervals as illustrated in (3.59). Let
n
∗
0,h
= ||δ
∗
0,h
||
be the length of the small interval δ
∗
0,h
. In the event that n
∗
0,h
is large
enough, we may estimate using the law of large numbers:
1
n
0,h
d
w
c
∗
δ
0,h
,d
∗
δ
∗
0,h
+L
∼
⎧
⎨
⎩
, if L =0,
3
4
, if L =0.
(3.96)
The central limit theorem yields
1
n
∗
0,h
d
w
c
∗
δ
0,h
,d
∗
δ
0,h
+L
∼
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
N
.
,
(1 − )
n
∗
0,h
/
, if L =0,
N
.
3
4
,
3
16n
∗
0,h
/
, if L =0,
(3.97)
where N(γ,S) is a normal distribution with the expectation of γ and
variance of S.
4. Using (3.93) and (3.96) and the properties of composite renewal processes,
we find that for the hybrid mutations, the error estimate of the uniform
alignment of the stochastic sequences is given by
1
n
a
w(C
∗
,D
∗
) ∼
1
+
2
1
p
1
+
2
p
2
(1 −
1
)+
3
p
3
+
4
p
4
, (3.98)
where
τ
, τ =1, 2, 3, 4 are the strengths of the τ mutation stream, and
that p
τ
, τ =1, 2, 3, 4 are the lengths of the type-II, type-III and type-IV
mutations, respectively. The reader is referred to Chap. 2 for more de-
tail.
106 3 Modulus Structure Theory
3.5.4 Local Modification of Sequence Alignment
In Examples 13 and 14, and in the proof of Theorem 16, we may find that
uniform alignment and the minimal penalty alignment are not perfectly com-
patible. There is a minor difference that can be addressed with a local mod-
ification. The basic purpose of sequence alignment is to find the mutation
relationship between different sequences, that is, to determine their uniform
alignments. However, we do not know whether the uniform alignment of two
sequences has been realized. Therefore, we instead determine the minimal
penalty alignment to approximate the uniform alignment because the min-
imal penalty alignment may be accurately computed. A local modification
allows us to estimate the uniform alignment since the minimal penalty align-
ment approximately determines the boundary of uniform alignment. Local
modification is a re-computation based on the output from sequence align-
ment in order to reduce the penalty. If (A
,B
) is the alignment output, the
local modification is stated as follows:
W-1 Permute the virtual symbols in A
and B
with the nearest nonvirtual
symbols.
W-2 Insert or delete one or more virtual symbols in both A
and B
simul-
taneously.
W-3 At the tails of the aligned sequences, we may insert or delete a number
of virtual symbols, in the hopes that this process reduces the magnitude
of the total error.
Example 16. The following shows three local modifications:
1. If
C = (00231(444)312(0021)3200231) ,
D = (00231(221)130(4444)3200231) ,
then the alignment error is d
H
(A
,B
) = 10. If we perform local modifica-
tion W-2 such that the output (A
,B
)is
C
= (00231312002(1)3200231) ,
D
= (00231221130(4)3200231) ,
then d
H
(C
,D
)=7<d
H
(A
,B
).
2. If
C = (00231(44444)3123200231) ,
D = (00231(22312)1303200231) ,
the alignment error is d
H
(A
,B
) = 8. If we perform local modification
W-1 such that (A
,B
)is
C
= (00231(44)312(444)3200231) ,
D
= (00231(22)312(130)3200231) ,
then d
H
(C
,D
)=5<d
H
(A
,B
).
3.6 Exercises 107
3. If
C = (00231312002(1)32000231) ,
D = (00231221130(4)32002310) ,
the alignment error is d
H
(A
,B
) = 11. If we perform local modification
W-3 such that (A
,B
)is
C
= (00231312002(1)3200(0)231(4)) ,
D
= (00231221130(4)3200(4)231(0)) ,
then d
H
(C
,D
)=9<d
H
(A
,B
).
Based on these examples, we find that all of the local modification operations
can reduce alignment error. Through a modification, we can approximate
a uniform alignment by a minimal penalty alignment, and obtain the modulus
structure of type-III and type-IV mutations.
3.6 Exercises
Exercise 12. Describe the relationship between modulus structure theory
and random mutations. Give the modulus structure of the sequence obtained
in Exercise 11.
Exercise 13. Prove Theorems 9, 10, 11, 12, and 15.
Exercise 14. For the given sequences
⎧
⎪
⎨
⎪
⎩
A = 11010201032213020103211022301 ,
B = 110102021010322001302110103210311022301 ,
C = 1101033320210103220013021100010321022311022301 ,
complete the following tasks:
1. Show that B is the expanded sequence of A,andC is the expanded se-
quence of B, and therefore, that C is the expanded sequence of A.
2. Give the three expanded modes by which B mutated from A, C mutated
from B,andC mutated from A. Also give the corresponding shifting
functions.
3. Give the three different compressed modes by which B compressed into
A, C compressed into B,andC compressed into A.
4. Give the operators of the expanded modes by which B mutated from A,
C mutated from B,andC mutated from A, showing the computation
procedure.
5. Compute the minimum penalty alignments based on the Hamming penalty
matrix and the SP-function condition, and compute the value of the SP-
penalty.
