Шемякин Е.И., Смирнов Н.Н., Нигматулин Р.И., Натяганов В.Л. (редакторы) Газовая и волновая динамика

Подождите немного. Документ загружается.

К вопросу о единственности построения решения

задачи Прандтля

Кончакова Н. А.

Не единственность выбора полей скольжения и распределения скоростей в клас-

сических решениях задачи о штампе по схеме жесткопластического тела указывает

на необходимость привлечения различных дополнительных соображений и исполь-

зования экспериментальных наблюдений. Показанная [1] положительность диссипа-

тивной функции, позволяет рассмотреть теоремы единственности решения краевых

задач для упругопластических тел. Представление диссипативной функции отража-

ет основные механические предположения, положенные в основу математической

модели. Гипотеза о совпадении главных направлений тензоров напряжений и дефор-

маций (скоростей деформаций) в пластическом состоянии является достаточно силь-

ным требованием при построении модели деформирования [1], поскольку в реальных

экспериментах достаточно часто имеет место отклонение от подобия тензоров [2].

Будем рассматривать соосность тензоров напряжений и скоростей деформаций, а от

их подобия следует отказаться. Тогда существенным является выбор инвариантов

напряженного и деформированного состояний, основанный на физической интер-

претации процессов диссипации энергии [3] и отражающий связь с площадками

максимальных касательных напряжений T и главными сдвигами Γ [4].

Проблема построения единственного решения распределения скоростей требует

обсуждения нескольких вопросов:

1. Какие типы краевых условий допускает теорема единственности в уравнениях

для деформаций?

2. Как поступить в том случае, когда используются краевые условия в напря-

жениях? Каким образом строить решения, если имеются смешанные условия

(например, под штампом)?

3. Какие дополнительные краевые условия следует поставить в областях с угло-

выми точками?

Обратимся к записи уравнения энергии [1]:



¯σ

· ¯uds +



F ·¯udτ =2



Wdτ +



Ddτ, (1)

где W — положительно определенная квадратичная форма напряжений или дефор-

маций для упругих состояний; скалярное произведение ¯σ

· ¯u включает напряжения

и перемещения (от полных деформаций); диссипативная функция D, выписанная

при условиях полной пластичности, положительна при всех значениях характери-

стических параметров. Выбор нового набора инвариантов обуславливает отсутствие

344

подобия тензоров напряжений и деформаций и позволяет перейти и описанию кине-

матики деформирования с помощью перемещений (скоростей перемещений) [4]. Для

этого вводятся дополнительные, независимые кинематические параметры — углы по-

ворота элементов среды ω и углы наклона главных направлений тензора деформаций

ψ [5, 6]. Соотношения, описывающие необратимую деформацию для предлагаемой

синтетической модели, приведены в работах [5, 6] и имеют вид:

∂ ˜ω

∂x

− cos 2ψ ·

∂ψ

∂x

+ sin 2ψ ·

∂ψ

∂y

=0,

∂ ˜ω

∂y

+ sin 2ψ ·

∂ψ

∂x

+ cos 2ψ ·

∂ψ

∂y

=0,

(2)

где ω =



∂v

∂x

−

∂u

∂y



, tg2ψ ==

−ε

, ˜ω =

Система принадлежит к гиперболическому типу и имеет два семейства веще-

ственных характеристик

= ctgψ,

= −tgψ, (3)

которые определяют сетку реальных линий скольжения, аналогичных линиям сколь-

жения в теории напряжений. Соотношения на характеристиках имеют вид:

˜ω + ψ = α = const, ˜ω − ψ = β = const. (4)

Указанные линии скольжения есть реально наблюдаемые во многих эксперимен-

тах линии разрушения материала [7], а также линии образования регулярных блоч-

ных структур в первоначально однородном теле [4, 5, 7].

Для иллюстрации приведенных в [6] свойств реальных линий скольжения, рас-

смотрим задачу о вдавливании штампа на податливом (с учетом необратимых дефор-

маций) основании. Штамп жесткий, трение на поверхности контакта отсутствует. В

предельном состоянии штамп движется вниз со скоростью

V .Решениевнапря-

жениях единственно и совпадает с решением Прандтля: в предельном состоянии

распределение давления под штампом равномерное. Задача имеет ось симметрии

x =0, поэтому естественно рассмотреть одну часть пространства и отобразить ре-

шение относительно указанной оси. Поле скольжения (рис. 1) строится следующим

образом [8]:

В ∆BED, в силу заданных краевых условий (прямолинейная граница, свободная

от усилий), имеет место простое сжатие, параллельное границе

σ = −k, θ=

Вдоль характеристик выполняются соотношения

α =

− θ = const,

345

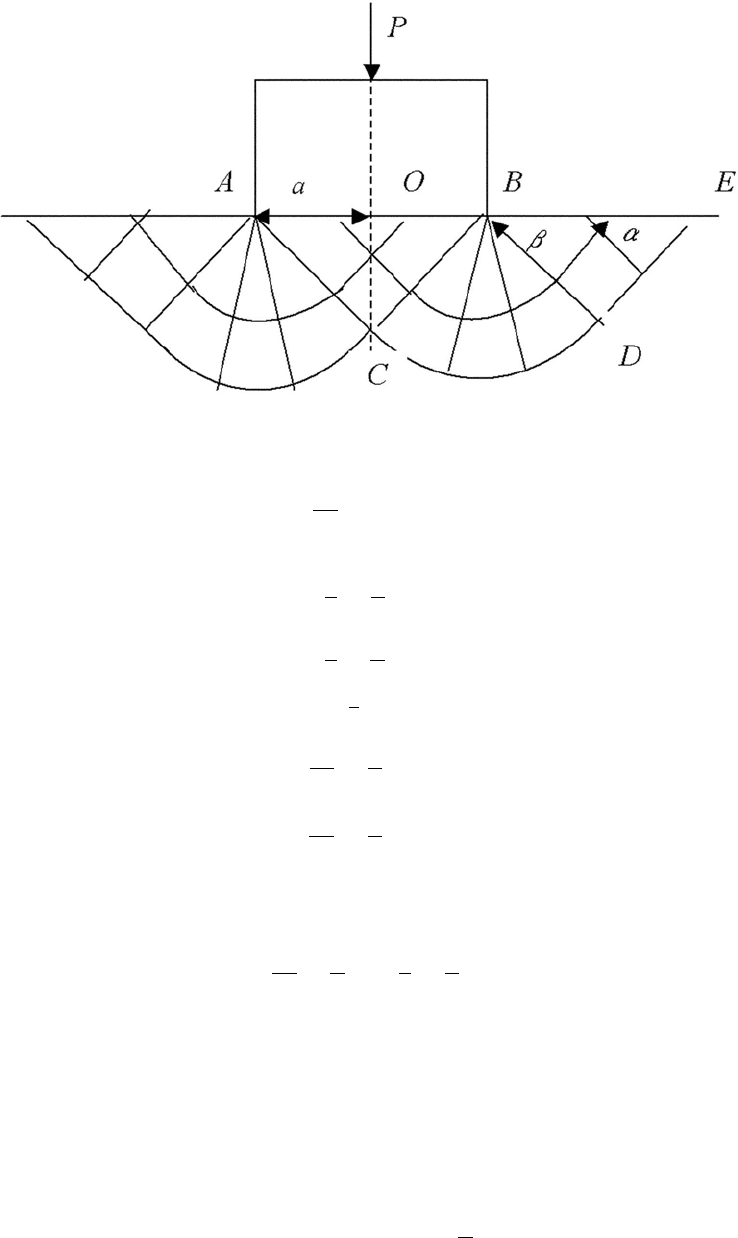
Рис. 1.

β =

+ θ = const.

В рассматриваемом случае

α = −

−

= const,

β = −

= const.

В ABC давление σ неизвестно, а θ =

. Вдоль характеристик

α =

= const,

β =

−

= const.

Треугольные области соединены центрированными полями. Вдоль α-линии параметр

α должен быть постоянен, следовательно α

ABC

= α

BED

= −

−

Откуда получаем σ

ABC

= −k (1 + π). Известно, что

= σ − k sin 2θ,

= σ + k sin 2θ.

Поэтому в зоне под штампом

= −k (1 + π) − k sin 2



−



= −kπ,

346

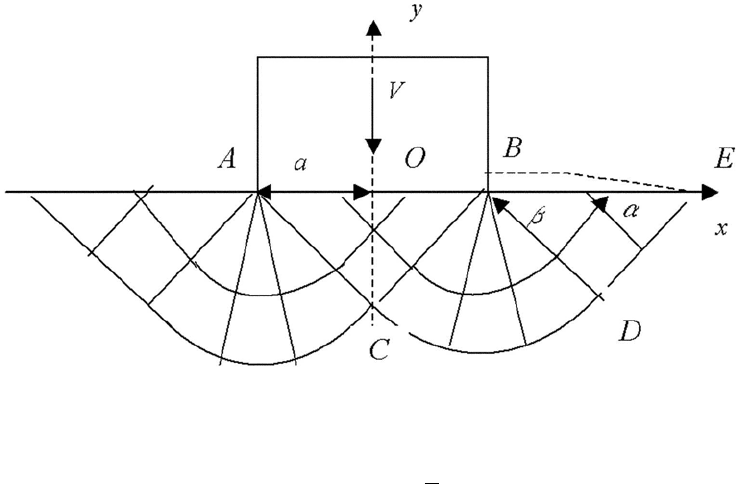
Рис. 2.

= −k (1 + π)+k sin 2



−



= −k (2 + π) .

Предельная нагрузка P

∗

dx =2ka (2 + π)

При построении поля скоростей логично обсудить вопрос о краевых условиях.

Напряжения всюду в пластической области известны. На границе y =0отсутствует

трение на поверхности и напряжение σ

. То есть,

при |a| <xнапряжения σ

= τ

=0. (5)

По условию задачи штамп движется вниз со скоростью

V .Следовательно,краевые

условия при |a| >x V =0, τ

=0. Таким образом, в точках A и B (рис. 2) происхо-

дит смена типов краевых условий: до рассматриваемых точек задаются напряжения,

а внутри штампа граничные условия описывают поведение перемещений.

Точки A и B являются особыми. Покажем, что в них требуется задать допол-

нительные краевые условия [9]. Классические решения задачи свидетельствуют о

том, что условие непрерывности перемещений в угловых точках не обеспечивает

единственности решения [8].

Рассмотрим область деформирования под штампом. На границе AB задано V =0,

т.е. ω = ω

=0, ψ = ψ

=0. Следовательно, решается задача Коши (в силу симметрии

рассмотрим только область OBC). Разделим отрезок OB на малые части точками

(0, 0), (1, 1), (2, 2) ...(m, m). Значения ˜ω и ψ в узлах, ближайших к дуге, найдем из

условий постоянства параметров α и β на характеристиках (4)

˜ω

m,m

+ ψ

m,m

= α =˜ω

m,m+1

+ ψ

m,m+1

˜ω

m+1,m+1

− ψ

m+1,m+1

= β =˜ω

m,m+1

− ψ

m,m+1

где ˜ω

m,m

, ψ

m,m

есть соответствующие значения переменных в узлах сетки. Из по-

следних уравнений получим выражения для определения неизвестных ω и ψ в про-

347

извольном узле (m, n), (n>m):

˜ω

m,n

(˜ω

m,n−1

+˜ω

m+1,n

+ ψ

m,n−1

− ψ

m+1,n

) ,

m,n

(ψ

m,n−1

+ ψ

m+1,n

+˜ω

m,n−1

− ˜ω

m+1,n

) .

Данные соотношения позволяют вычислить параметры ˜ω и ψ в ∆OBC .При

заданных граничных условиях имеем:

˜ω

0,1

=0,ψ

0,1

= ψ

;˜ω

1,2

=0,ψ

1,2

= ψ

; ... ;

˜ω

m,1

=0,ψ

m,1

= ψ

; ... ;˜ω

m,n

=0,ψ

m,n

= ψ

; ...

Значение переменной ˜ω всюду в области OBC равно нулю, а переменная ψ = ψ

во

всех точках этой области. Таким образом, в пластической зоне под штампом, имеет

место равномерное прямолинейное поле деформаций [6]. Реальными линиями сколь-

жения будут два ортогональных семейства параллельных прямых направленных под

углом θ =

к границе (рис. 2). В данном поле линий скольжения характеристики ω

и ψ постоянны. Таким образом, все элементы поворачиваются одинаково на угол ω,

а также ψ — угол между главным направлением тензора деформаций и осью Ox —

сохраняет свое постоянное значение.

Проанализируем поведение перемещений в рассматриваемой области. Соотноше-

ния для деформаций имеют вид [6]:

= −

cos 2ψ,

=Γ

sin 2ψ.

Подставим их в известные [5] формулы для приращений перемещений:

du =

∂u

∂x

dx +

∂u

∂y

dy = ε

dx +



− ω



dy,

dv =

∂v

∂x

dx +

∂v

∂y

dy =



+ ω



dx + ε

dy.

С учетом малости параметра ψ, получим:

du = −

dx +Γ

dy,

dv =Γ

dx +

dy.

(6)

Уравнения (6) совместно с условиями (4) позволяют находить смещения u и v

вдоль характеристик в области OBC.

348

Выше было показано, что на характеристике BC ω равно нулю. Однако, в точке

Bω=0, что физически объясняется процессом вдавливания штампа. Как видим, в

точке B не только происходит смена краевых условий, но и меняется значение пере-

менной ω. Значит, для единственности решения необходимо ввести дополнительные

краевые условия: либо задать ω — повороты волокна (элемента), либо указать изме-

нение величины ψ.

ВзонеBED сетка по напряжениям известна. Работая с уравнениями для дефор-

маций (2) и краевыми условиями для напряжений (5), из физических соображений

можно предположить искажение границы y =0— BE. Возмущения ω и ψ могут быть

вычислены в области BED, если проведен полный анализ решения в веере BCD.

Разрыв величины ω,введенныйвточкеB, распределяется на характеристических

линиях веера. Тогда [ω] компенсируется внутри области.

Таким образом, в точках A и B следует дозадать разрыв перемещений или момент

сил (поворот), что обеспечит единственность решения как упругой, так и упругопла-

стической задач.

Литература

[1] ШемякинЕ.И.Диссипативная функция в моделях идеальных упругопласти-

ческих тел. — Докл. РАН, Механика, 2001, Т. 376, № 4.

[2] Христианович С. А., Шемякин Е. И. О плоской деформации пластического

материала при сложном нагружении. — Изв. АН СССР, МТТ, 1969, №5.

[3] ШемякинЕ.И.Об инвариантах напряженного и деформированного состояния

в математических моделях механики сплошной среды. — Докл. РАН, Меха-

ника, 2000, Т. 373, №5.

[4] Шемякин Е. И. Синтетическая теория прочности. Часть I. — Физическая ме-

зомеханика, 1999, №2.

[5] Шемякин Е. И. О хрупком разрушении твердых тел (плоская деформация). —

Изв. РАН, Механ. тверд. тела, 1997, №2.

[6] Кончакова Н. А. О построении моделей сплошных сред с несимметричными

тензорами. — Вестн. Моск. ун-та, Сер.1, Математика, Механика, 2002, № 4.

[7] Ревуженко А. Ф. Механика упругопластических сред и нестандартный ана-

лиз. — Новосибирск, 2000.

[8] Качанов Л. М. Основы теории пластичности. — М., 1969.

[9] ШемякинЕ.И.О краевых задачах теории упругости для областей с угловыми

точками (плоская деформация). — Докл. РАН, Механика, 1996, Т. 347, №3.

349

Модель движения разгонных вихрей в следе за

цилиндром

Козлов В. П.

1. Введение

При решении задач аэродинамики широко используются приближенные математи-

ческие модели. Эти модели, в частности, служат для решения задач обтекания с

образованием отрывных зон течение в которых, как правило, является нестационар-

ным. Большое распространение получил метод дискретных вихрей [1], разработан-

ный в начале XIX века Розенхидом [2] и основанный на моделировании отрывных

зон «облаком» свободных дискретных вихрей. Достаточно полный анализ подходов

при решении подобных задачах в рамках модели идеальной несжимаемой жидкости

приводится в книге [3].

В данной статье предлагается один из возможных вариантов модели течения в

зоне отрыва в двухмерном случае. В качестве примера будет рассмотрена задача по-

перечного обтекания кругового цилиндра радиуса r дозвуковым потоком, мгновенно

преобретающим постоянную скоростью V

∞

. Из эксперимента [4, 5] известно, что в

этом случае в ближнем следе за цилиндром образуется область возвратного течения,

представляющая из себя пару разгонных вихрей. В течении некоторого времени эта

область увеличивается, а разгонные вихри остаются симметрично расположенными

относительно оси, проходящей через центр цилиндра в направлении скорости потока.

На расстоянии около полутора диаметров от цилиндра вихри теряют устойчивость

и поочередно сходят в поток. Задача состоит в том, что бы в рамках идеальной

несжимаеммой жидкости описать движение разгонных вихрей до момента потери их

устойчивого симметричного положения.

В основу данного подхода легли идеи Брайсона, предложенные им в работе [6]. В

этой работе в рамках потенциальной модели течения разгонные вихри моделируют-

ся парой вихрей, имеющие не нулевую составляющую скорости относительно частиц

жидкости dξ

/dt,гдеξ

(t) - комплексная координата положения вихря и переменную

по времени циркуляцию Γ

= Γ

(t). В [6] вводятся две вихревые пелены, соединяю-

щие вихри с поверхностью цилиндра в точке отрыва ξ = ξ

и выводится уравнение

движения каждого вихря из соотношений баланса сил, действующих на вихревую

пелену и вихрь. При этом предполагается, что вихревая пелена испытывает давле-

ние со стороны жидкости и, следовательно является некотой материальной твердой

линией. Понятия вихревой пелены и дискретных вихрей, введенные в работе [6] не

согласуются с классическим определением дискретного вихря и вихревого слоя [2].

В [2] каждый вихрь пелены или слоя «вморожен» в среду и свободно сносится по-

током, имея при этом постоянную циркуляцию и скорость, равную скорости частиц

жидкости потенциального течения. Таким образом, принятые в [6] предположения

350

делают некорректным описание течения в следе за телом в рамках используемой

модели.

В данной работе предлагается квазистационарная схема течения в следе за ци-

линдром. Уравнения движения вихрей выводятся строго при помощи закона об из-

менении колличества движения некоторого объема содержащего вихри. Основанием

для рассмотрения квазистационарной модели послужили, например, работы [4, 5, 7],

в которых приводятся результаты экспериментов по визуализация течения в следе за

цилиндром, помещенного в поток с постоянной скоростью V

∞

. В этих работах было

установлено, что скорость центров разгонных вихрей достаточно мала по сравнению

со скоростью свободного потока вблизи отрывной зоны. Таким образом в каждый

момент времени течение можно считать потенциальным, а вихри в следе стационар-

ными, положение и циркуляция, которых изменяется и зависит от времени как от

параметра. Похожая картина течения и формирования разгонных вихрей набдюдает-

ся, также при обтекании плоской пластины, расположенной в поперечном потоке [5]

и крылового профиля [7].

В действительности процесс формирования ближнего следа намного сложнее опи-

санного выше и о справедливости предлагаемого подхода можно судить лишь после

сравнения расчетных результатов с экспериментальными данными. Ниже приводится

вывод уравнений движения вихрей.

2. Вывод уравнения

Рассматривается двумерное потенциальное течение идеальной несжимаемой жидко-

сти в которую помещено тело. Введем комплексную координату ξ = x + iy и W -

комплексный потенциал скорости потока. Предположим, что W = ϕ + iψ,гдеϕ -

действительный потенциал, ψ - функция тока, есть суммарный потенциал от свобод-

ного течения жидкости, от тела в потоке и от вихря (или вихрей) в следе за телом,

рис. 1. Характер течения жидкости таков, что выполняется уравнение Лапласса:

∆ϕ = 0 (1)

Комплексный потенциал W в общем виде можно представить как:

W = W(ξ,Γ

(t),ξ

(t)) (2)

Здесь ξ

= ξ

(t) - комплексная координата положения вихря, Γ

= Γ

(t) - циркуляция

вихря. Пусть l некоторый замкнутый контур, внутри которого содержится вихрь

и Σ - объем жидкости, содержащейся внутри контура, Риг.1. По предположению

голоморфности функции W внутри контура l, W можно представить в виде:

W = Γ

ln(ξ − ξ

)+C

+ C

(ξ − ξ

)+C

(ξ − ξ

)

+ ... (3)

Здесь C

, C

, ··· = const. Вектор сопряженной комплексной скорости

V опреде-

ляется как:

V =

dξ

, где

V = u − iv (4)

351

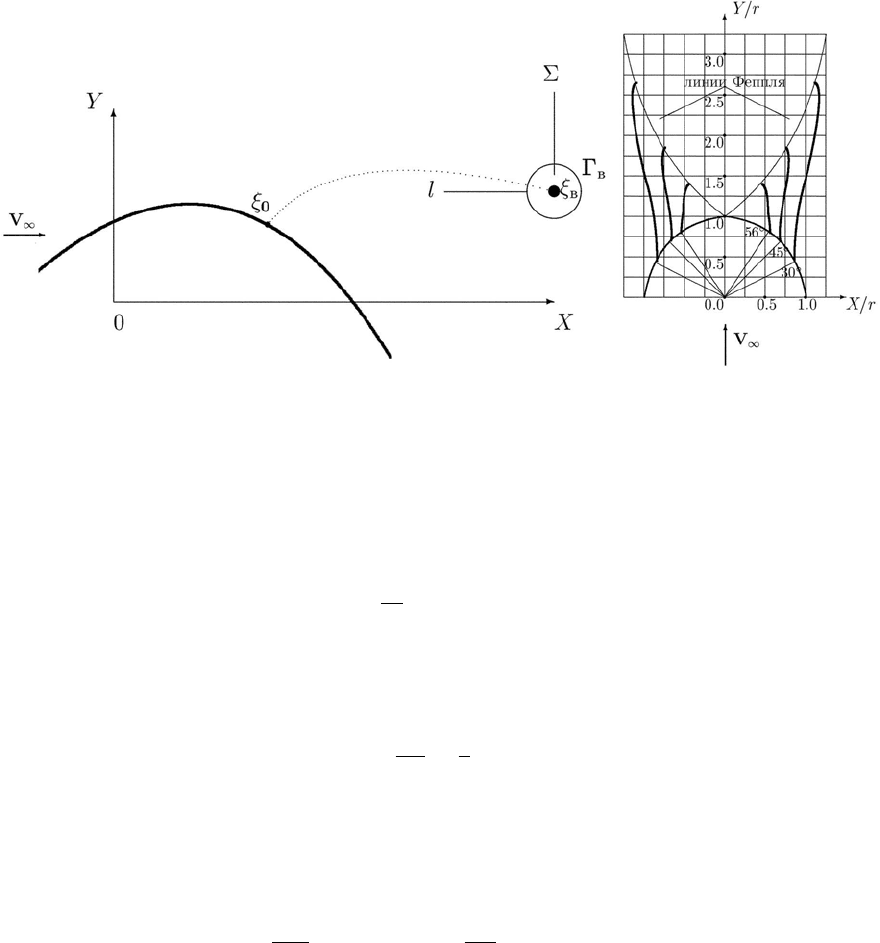
Рис. 1. Схема расположения тела в потоке и вихря в следе Рис. 2. Траектории движения

вихрей в следе за цилиндром,

расчитанные по уравнению [7]

для трех положений углов от-

рыва

Запишем закон об изменении колличества движения объема жидкости, содержаще-

гося внутри l:

= F + P (5)

В уравнении (5) I =

(u + iv)dσ - импульс сил объема Σ, F - массовые силы, P -

поверхностные силы давления, определяемые уравнением:

P = ip = i(p

−

∂ϕ

∂t

−

ρ(u − iv)(u + iv)) (6)

Уравнение (6) есть интеграл Коши-Лагранжа. Устремляем объем к нулю и из-

за малости объема пренебрегаем массовыми силами. После подстановки условий

(3),(4),(6) в (5) и интегрирования по контуру l левой и правой части уравнения (5)

получим:

dΓ

(ξ

− ξ

)+Γ

(

dξ

−

) = 0 (7)

В (7)

= V|

ξ=ξ

- скорость жидкости в точке ξ

, dξ

/dt - скорость вихря, ξ

-ком-

плексная координата точки отрыва, которая задается. В окрестности точки отрыва

характер течения аналогичен тормозящему потоку в двугранном угле, образованном,

в данном случае поверхностью тела и отошедшей от тела линией тока вследствии

отрыва течения [7]. Предполагается, что ξ

= const и из условия того, что в точке

отрыва скорость равна нулю определяется циркуляция вихря Γ

(t):

(

ξ=ξ

= 0 (8)

352

Уравнение (7), аналогичное полученному в [6] служит для определения координаты

вихря ξ

в зависимости от времени.

В случае обтекания кругового цилиндра уравнение (7) необходимо решать для

каждого, из пары симметрично расположенных относительно оси 0Y вихрей модели-

рующие разгонные. Вихри имеют противоположные по знаку циркуляции, с положи-

тельным направлением взятом против часовой стрелки. Точки отрыва расположены

симметрично относительно оси 0Y . Комплексный потенциал, в этом случае можно

представить в виде:

W = W

+ W

(9)

В (9) W

- потенциал от свободного потока и диполя, моделирующего цилиндр, W

- потенциал от пары вирхей, расположенных в точках ξ

и −

, W

- потенциал от

«зеркальных» отображений вихрей в следе из вне, во внутренность цилиндра, распо-

ложенных в точках r

/ξ

и −r

. Заметим, что в приведенной схеме расположения

вихрей суммарная их циркуляция равна нулю. В явном виде W можно записать

как [4]:

W(ξ, t)=−iV

∞

(ξ −

) −

iΓ

2π

(ξ − ξ

)(ξ + r

/ξ

)

(ξ −

)(ξ + r

)

−

iΓ

2π

ln(−

) (10)

Условие (8), в случае цилиндра запишется как:

Γ =(2πV

∞

)

(ξ

− ξ

)(

−

)(ξ

)(

+ ξ

)

(ξ

− r

)(ξ

)

(11)

3. Результаты расчетов

Расчеты проводились для трех положений точек отрыва ξ

= r

iθ

, θ

=30

◦

;45

◦

;56

◦

и r

=0.5% от радиуса цилиндра. В расчетах было установлено, что вихри, удаляясь

от поверхности цилиндра, асимптотически приближаются к положению на линии

Феппля [4], рис. 2. При этом, расчетное время за которое вихри проходят расстоя-

ние от точки отрыва до линии Феппля соответствует экспериментально замеренному

времени в работе [5]. В [5] измерялось время прошедшее от момента начала образо-

вания разгонных вихрей у поверхности цилиндра до момента потери их устойчивого

положения и схода в поток. Согласие экспериментальных и расчетных данных под-

тверждает качественно верное описании течения в отрывной зоне за цилиндром.

Рассмотренную модель можно использовать, видимо, и для случая других плохооб-

текаемых тел на участке формирования разгонных вихрей. При стационарном от-

рывном обтекании в дальнем следе образуется вихревая дорожка Кармана. Такое

течение достаточно хорошо описывается моделью дискретных вихрей [1]. Предложе-

ную, в данной работе модель можно использовать на участке формированния вихрей

после отрыва пограничного слоя в ближнем следе до образования дорожки Кармана.

353