Шемякин Е.И., Смирнов Н.Н., Нигматулин Р.И., Натяганов В.Л. (редакторы) Газовая и волновая динамика
Подождите немного. Документ загружается.

Литература
[1] Куксенко Б. В. О понятиях сила и работа в классической механике. — Вестник
МГУ, Сер.1, Математика, механика, 2001, № 5.
[2] Куксенко Б. В. О возможности существования второй относительности. —
Вестник МГУ, Сер.1, Математика, механика, 2002, № 1.
[3] Вихман Э. Квантовая физика. — Берклеевский курс физики, т.4, М. Наука,
1974.
314

Модель газовой детонации
Гендугов В. М.
Данная работа является развитием газодинамики воспламенения [1] — теории
движения реагирующей смеси, альтернативной традиционной газодинамике горения.
В ее основе лежит представление о том, что в смеси с несколькими наблюдаемы-
ми реакциями процесс превращений осуществляется по макромеханизму связанных
реакций [1, 2]. В рамках газодинамики воспламенения построена модель стационар-
ной самоподдерживающейся детонации, исследована структура волны и выведены
уравнения, определяющие ее скорость.
1. Исследование начнем с вывода уравнений газодинамики воспламенения. Рас-
смотрим вначале уравнения газодинамики горения, записанные в пренебрежении
явлениями переноса. Такая система включает уравнения неразрывности, количества
движения, энергии, состояния и концентраций компонентов смеси. После исключе-
ния зависимых концентраций с помощью уравнений закона сохранения атомов
c
k
=
n
i=1
ϕ
ki
c
i
+ ϕ
k
,k=1,...,N (1)
перечисленные уравнения принимают вид
dρ
dt
+ ρ div V =0, (2)
ρ
dV
dt
+ grad p =0, (3)
dh
dt
=
dp
dt
, (4)
ρ = ρ (h, p, c
i
) , (5)
dc
i
dt
= E
i
, (6)
ρ, p, h, V — плотность, давление, энтальпия и вектор скорости; c
k
—массовая
концентрация (доля) k-го компонента; E
i
— скорость i-й наблюдаемой реакции;
d
dt
=
∂
∂t
+ V · grad ; N − N
a
= n; N, N
a
— число компонентов и сортов атомов;
ϕ
ki
,ϕ
k
= const.
Обратим внимание на то, что прежде чем принять замкнутую систему (2) – (6)
за основу построения теории необходимо предварительно сформулировать гипотезу о
зависимости или независимости системы. Газодинамика горения строится в рамках
гипотезы о независимости уравнений (2) – (6). Тем самым неявно сформулирова-
на физическая гипотеза (основное положение газодинамики горения): наблюдаемые
315
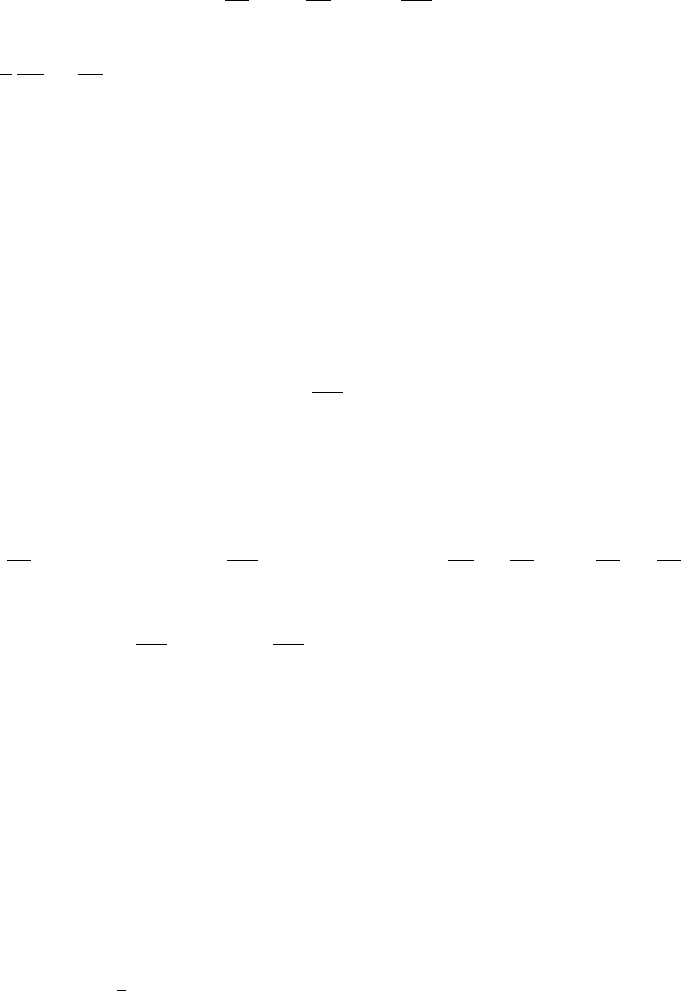
реакции E
i
функционально независимы. Выясним следствие этого положения. За-
пишем уравнение состояния (5) в дифференциальной форме и, привлекая (4), (6),
приведем его к виду
dp
dt
− a
2
f
dρ
dt
=
n
i=1
∂ρ
∂c
i
E
i
, (7)
где a
−2
f
=
1
ρ
∂ρ
∂h
+
∂ρ
∂p
,a
f
— замороженная скорость звука.
Из (7) следует, что термодинамические параметры смеси испытывают локальное
влияние скоростей реакции через их комбинацию в правой части уравнения, которая
в силу функциональной независимости реакции отлична от нуля при E
i
=0.
В стремлении описать реальное поведение горючей смеси [3, 4] мы должны отка-
заться от основного положения газодинамики горения и строить теорию, газодинами-
ку воспламенения, в основе которой лежит гипотеза о зависимости уравнений (2) –
(6). При этом одной из возможной альтернативы, допускаемой законами сохранения
и уравнением состояния, является функциональная зависимость между скоростями
реакций
n
i=1
∂ρ
∂c
i
E
i
=0 (8)
которую будем называть соотношением связанности n реакций.
Следствием связанности реакций является расщепление (7), которое приводит к
распаду исходной системы уравнений на две подсистемы
dρ
dt
+ ρ div V =0,ρ
dV
dt
+ grad p =0,ρ
dh
dt
=
dp
dt
,a
2
f
dρ
dt
=
dp
dt
(9)
и
n
i=1
∂ρ
∂c
i
E
i
=0,
dc
j
dt
= E
j
,j=1,...,(n − 1) . (10)
Эти уравнения будем называть уравнениями газодинамики воспламенения.
2. Одним из центральных в теории детонации является вопрос о состоянии исход-
ной горючей смеси газов, способной детонировать. Напомним, что в рамках тради-
ционной термодинамики доказано [5, 6], что она химически неравновесна. При этом
для всех типов протекания реакций равновесное состояние оказывается единствен-
ным, а соответствующий ему состав смеси в основном состоит из продуктов реакции.
Вместе с тем в опытах наблюдается совершенно иная картина [3]. При параметрах
вне области воспламенения смесь ведет себя как нейтральная среда. Рассмотрим
поведение покоящейся реагирующей среды в рамках газодинамики воспламенения.
Из (9) следует, что процесс превращений развивается в условиях p, ρ, h = const и
e = const (e = h −
p
ρ
= const, e — внутренняя энергияя). В указанных условиях
уравнение состояния (5) приобретает качественно новый смысл — соотношение свя-
занности концентраций. Из сказанного следует, что реакции в неподвижной смеси
подчиняются уравнениям
p = const, ρ = const, h = const, ρ = ρ (h, p, c
i
) (11)
316

dc
j
dt
= E
j
(j =1,...,(n − 1)) (12)
Согласно основному положению термодинамики состояние химического равнове-
сия изолированной системы характеризуется максимумом энтропии (S)вусловиях
протекания реакций. Вматематическом плане вывод уравнений химического равно-
весия при связанных реакциях сводится к обычной задаче условного максимума
функции S :
δS =0 (13)
δ
2
S 0 (14)
при голономных связях (11). Воспользуемся уравнением второго начала термодина-
мики в переменных h, p, c
i
которое с учетом вида вариаций (11) запишется так
δS =
n−1
j=1
∂S
∂c
j
+
∂S
∂c
n
∂c
n
∂c
j
δc
j
. (15)
Имея в виду (13), из (15) получим систему уравнений химического равновесия
при связанных реакциях
∂S
∂c
j
+
∂S
∂c
n
∂c
n
∂c
j
=0,j=1,...,(n − 1). (16)
При этом физически реализуемые решения (16) должны удовлетворять (14). Что-
бы конкретизировать условие (14), вычислим по формуле (15) вторую вариацию эн-
тропии:
δ
2
S =
n−1
j,e=1
A
je
δc
j
δc
e
,
где A
je
=
∂
2
S
∂c
j
∂c
e
+
∂
2
S
∂c
j
∂c
n
∂c
n
∂c
e
+
∂
2
S
∂c
e
∂c
n
∂c
n
∂c
j
+
∂
2
S
∂c
2
n
∂c
n
∂c
j
∂c
n
∂c
e
+
∂S
∂c
n
∂
2
c
n
∂c
j
∂c
e
—элемент
матрицы симметричной квадратичной формы (к.ф.).
В силу (14) к.ф. является отрицательно определенной, или отрицательной. Как
известно [7], к.ф. определенно отрицательна, еслиглавные миноры ее матрицым
g
порядка g удовлетворяют неравенствам Сильвестра
(−1)
g
g
> 0,g=1, ..., (n − 1). (17)
Назовем состояние смеси равновесным при связанных реакциях, если концентра-
ции являются решениями (16) и удовлетворяют неравенствам (17).
Рассмотрим ситуацию, когда к.ф. отрицательна. Таккак при этом хотя бы одно
из собственных значений равно нулю, то матрица к.ф. вырождена. Длятого чтобы
к.ф. былаотрицательной, необходимо и достаточно, чтобы отличные от нуля главные
миноры ее матрицы порядка g удовлетворяли неравенствам (17).
317
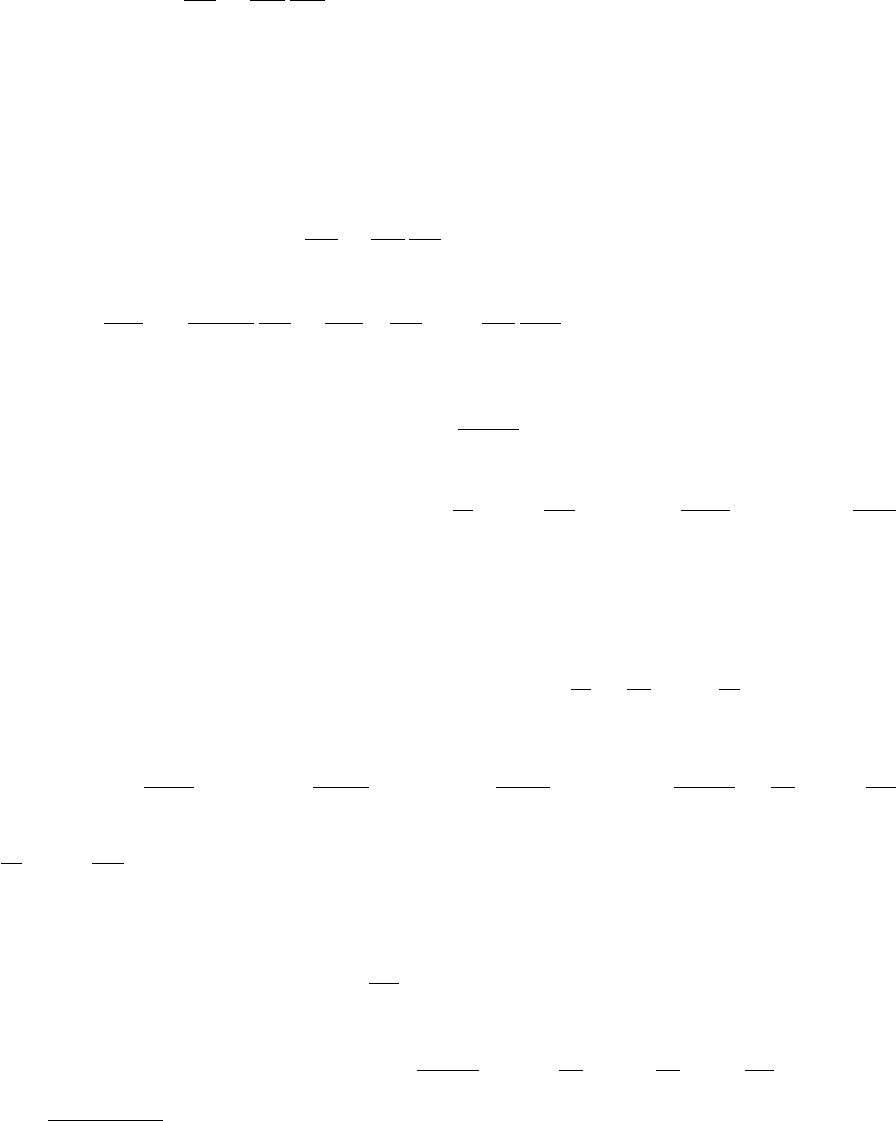
Назовем равновесное состояние смеси предельным, если концентрации являются
решениями системы уравнений
∂S
∂c
j
+
∂S
∂c
n
∂c
n
∂c
j
=0,
n−1
=0, (j =1, ..., (n − 1))
и при этих значениях выполняются оговоренные выше условия.
Основные свойства сред будем выяснять на примере смеси, реагирующей по ме-
ханизму двух связанных реакций (n =2). В этом случае состояние равновесия при
связанных реакциях определяется как решение уравнения (16). В то же время со-
стояние предельного равновесия находится как решение системы уравнений
∂S
∂c
1
+
∂S
∂c
2
dc
2
dc
1
=0,
1
=0, (18)
где
1
=
∂
2
S
∂c
2
1
+2
∂
2
S
∂c
1
∂c
2
dc
2
dc
1
+
∂
2
S
∂c
2
2
dc
2
dc
1
2
+
∂S
∂c
2
d
2
c
2
dc
2
1
.
3. Объектом дальнейших исследований является смесь политропных газов с урав-
нением состояния
p = ρR
h + Q
c
p
m
(19)
где R — абсолютная газовая постоянная;
1
m
=
N
k=1
c
k
m
k
; c
p
=
N
k=1
c
k
c
pk
m
k
; Q = −
N
k=1
h
◦
e
c
k
m
k
;
m
k
, h
◦
k
, c
pk
— молекулярная масса, энергия образования и теплоемкость при посто-
янном давлении k-го компонента.
Привлекая (1), Q, c
p
и m приведем к виду
Q = q
0
+
n
i=1
q
i
c
i
,c
p
= α
0
+
n
i=1
α
i
c
i
,
1
m
=
1
µ
0
+
n
i=1
c
i
µ
i
, (20)
где q
0
=
N
k=1
ϕ
k
h
0
k
m
k
, q
i
=
N
k=1
ϕ
ki
h
0
k
m
k
, α
0
=
N
k=1
ϕ
k
c
pk
m
k
, α
i
=
N
k=1
ϕ
ki
c
pk
m
k
,
1
µ
0
=
N
k=1
ϕ
k
m
k
,
1
µ
i
=
N
k=1
ϕ
k
i
m
k
.
С учетом (20) запишем (19) в форме
n
i=1
Q
i
e
i
n
i=1
c
i
M
i
+
n
i=1
l
i
c
i
+(1− ψ)=0, (21)
где безразмерные коэффициенты Q
i
=
q
i
h + q
0
,M
i
=
µ
i
µ
0
,L
i
=
α
i
α
0
,l
i
=
1
M
i
+ Q
i
− L
i
ψ,
ψ =
p
α
0
µ
0
Rρ (h + q
0
)
представляют собой постоянные величины в условиях (11).
318
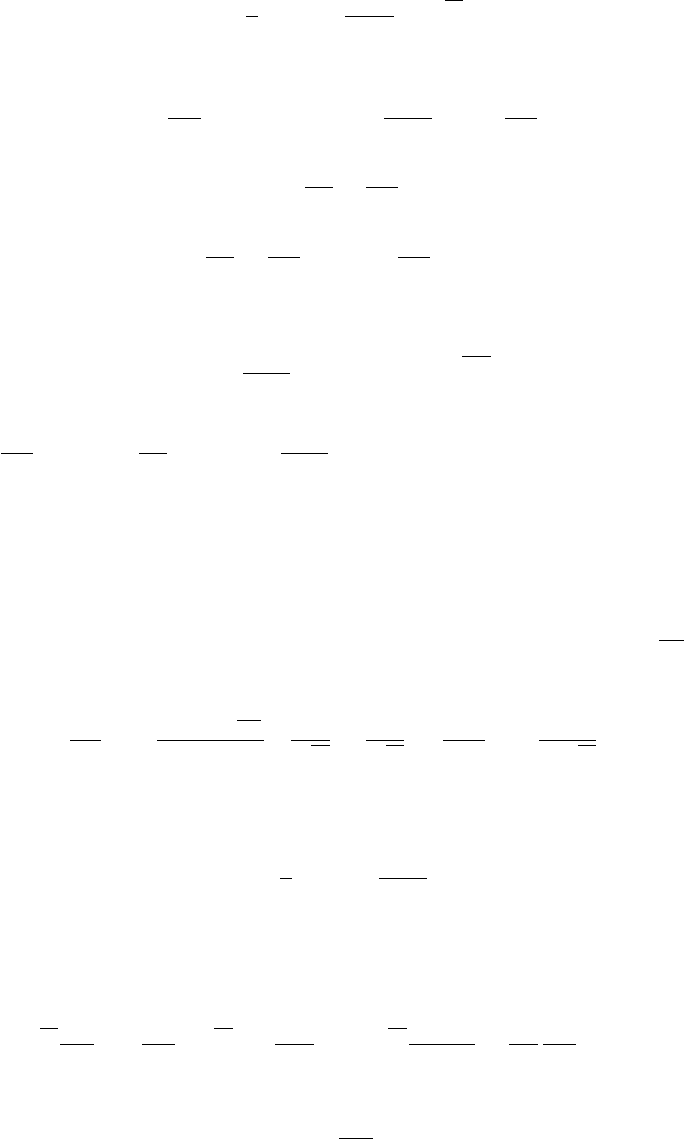
Выясним свойства (21) на примере смеси с двумя связанными реакциями (n = 2).
Для этого случая решим (21) относительно c
2
:
c
2
= −
1
2
ac
1
+
M
2
l
2
Q
2
±
√
F
, (22)
где
F = b
2
c
2
1
+2
M
2
Q
2
(al
2
− 2l
1
) c
1
+
M
2
l
2
Q
2
2
− 4
M
2
Q
2
(1 − ψ) ,
a =
Q
1
Q
2
+
M
2
M
1
,
b =
Q
1
Q
2
−
M
2
M
1
Q =0,
1
M
2
=0
.
При этом корни F имеют вид
c
1
1,2
= −
M
2
b
2
Q
2
al
2
− 2l
1
± 2
D
0
, (23)
где D
0
=
M
2
M
1
l
2
− l
1
Q
1
Q
2
l
2
− l
1
−
Q
2
b
2
M
2
(1 − ψ) .
В силу вещественности c
1
1
и c
1
2
ОДЗ c
1
удовлетворяет условию F 0.Если
в (23) D
0
< 0, то это условие удовлетворяется автоматически для всех c
1
(при
естественном ограничении). Интереснее, однако, случай D
0
> 0. В этой ситуации
интервал между корнями (23) очевидно, не входит в ОДЗ, иначе говоря, при D
0
>
0 не существует механизма связанных реакций. Отметим еще ряд особенностей
соотношения связанности концентраций (22) при D
0
> 0. Во-первых,
dF
dc
1
=0,во-
вторых, производные
dc
2
dc
1
=
−2F ±
dF
dc
1
4
1
√
F
=
θ
√
F
,
d
2
c
2
dc
2
1
= ±
D
F
√
F
на границе ОДЗ бесконечны, в-третьих, на границе ОДЗ уравнение (23) расщепля-
ется:
c
2
= −
1
2
ac
1
+
M
2
l
2
Q
2
, (24)
F =0. (25)
Запишем теперь систему уравнений предельного равновесия (18) с учетом вида
(23):
√
F
∂S
∂c
1
= θ
∂S
∂c
2
,
√
F
F
∂
2
S
∂c
2
1
+2θ
√
F
∂
2
S
∂c
1
∂c
2
±
D
0
8
∂S
∂c
2
=0.
Эта система имеет решение
F =0,
∂S
∂c
2
=0,
319

свидетельствующее о том, что термодинамическая функция предельного равновесия
в пространстве параметров p, ρ, h отделяет область G, где реализуются равновесные
состояния при связанных реакций, отобласти
G, где таких состояний не существует
(область воспламенения).
4. Рассмотрим покоящуюся смесь политропных газов способную детониро-
вать и находящуюся в равновесии при двух связанных реакциях при параметрах
(p = p
0
,h= h
0
,ρ= ρ
0
) из G. Тогда состав смеси (c
k
= c
k0
) является решением урав-
нения химического равновесия (16). Пусть по этой смеси с постоянной скоростью
D распространяется ударная волна (УВ), которая разогревает смесь и возбуждает в
ней реакции. Как и в работе [8] изменением состава смеси в скачке уплотнения пре-
небрегается. Тогда параметры горючей смеси перед и за УВ удовлетворяют обычным
соотношениям
ρ
0
D = ρ
s
u
s
= K, p
s
+
K
2
ρ
= p
0
+
K
2
ρ
0
,h
s
+
K
2
ρ
2
= h
0
+
K
2
2ρ
2
0
,
ρ
s
=
p
s
c
p0
m
0
R (h
s
+ q
0
)
,c
k
s
= c
k0
(k =1,...,N) .
(26)
Здесь u — скорость потока относительно УВ; c
p0
=
N
k=1
c
k0
c
pk
m
k
,
1
m
0
=
N
k=1
c
k0
m
k
,
q
0
=
N
k=1
c
k0
h
◦
k
m
k
;индексы0, s относятся, соответственно к параметрам перед и за УВ.
Тогда уравнения газодинамики воспламенения (9), (10) принимают вид
ρu = K,
dp
dx
=
K
2
ρ
2
dρ
dx
,
dh
dx
=
K
2
ρ
3
dρ
dx
,
dp
dx
=
1
a
2
f
dρ
dx
(27)
N
i=1
∂ρ
∂c
i
ε
i
=0;
dc
1
dx
=
E
1
U
= ε
1
. (28)
Комбинируя второе и четвертое уравнения (27), получим
1 − M
2
f
dρ
dx
=0
M
f
=
U
a
f
.
Из этого равенства следует, что в окрестности УВ параметры потока (p, ρ, h, u) по-
стоянные величины, равные их значениям на УВ.
Обратим внимание на то, что в зависимости от скорости УВ процесс превраще-
ний за ней развивается по одному из двух сценариев. Первый из них соответствует
ситуации, когда параметрыпотока за УВостаются в области G (вне области вос-
пламенения) и реакции, оставаясь связанными, приходят в состояние химического
равновесия. При этом параметры потока остаются постоянными, а волна распростра-
няется по горючей смеси, как по нейтральному газу. Такая ситуация имеет место до
320

тех пор, пока равновесие за УВне станет предельным. В данной работе мы ограни-
чимся этим качественным указанием о характере распространения УВ по первому
сценарию, предопределяющим исследование важной задачи о пределе инициирова-
ния детонации ударной волной.
Рассмотрим второй сценарий, когда параметры потока за УВ принадлежат области
воспламенения
G
. Тогда, в ударно сжатой горючей смеси с постояными парамет-
рами нет состояния равновесия при связанных реакциях. Так как на УВ реакции
связаны, то они остаются таковыми и вне окрестности (зоне индукции), в кото-
рой изменение состава определяется из второго уравнения (28) при фиксированных
значениях p и h (p = p
0
, h = h
s
)
x =
c
1
c
10
dc
ε
1
.
Поскольку равновесия нет, то на расстоянии
x = ζ =
c
1
c
10
dc
ε
1
, (29)
от УВ концентрация c
1
выходит на границу ОДЗ соотношения (22). В результате на
поверхности x = ζ (поверхность воспламенения) соотношение (22) расщепляется на
(24) и (25) с кризисом механизма связанных реакций. Далее при x>ζи в силу
неравновесности процесса c
1
принимает значение вне ОДЗ (22). Поэтому соотно-
шения (24) и (25) дополняет уравнение закона сохранения атомов (1) и движение
реагирующей смеси подчиняется традиционным уравнениям газодинамики горения
(2) – (6) с одной реакцией, но с уравнением состояния в форме (25). Имея в виду
сказанное, запишем (2) – (6) в системе координат, связанной с УВ (x>ζ)
ρu = K,
dp
dx
=
K
2
ρ
2
dρ
dx
;
dh
dx
=
K
2
ρ
3
dρ
dx
; F =0;
dc
1
dx
= ε
1
. (30)
Замечание 1. Так как (2) – (6) выводятся при условиях достаточной гладкости
производных, входящих в уравнения, то, естественно, при переходе к новой системе
координат условиянепрерывности градиентов параметров сохраняется.
Система уравнений (30) решается с начальными данными на поверхности вос-
пламенения
x = ζ, p = p
s
,h= h
s
,ρ= ρ
s
,u= u
s
,c
1
= c
1
1
. (31)
Запишем уравнение состояния (25) в дифференциальной форме
∂F
∂ρ
dρ
dx
+
∂F
∂p
dp
dx
+
∂F
∂h
dh
dx
+
∂F
∂c
1
dc
1
dx
=0.
Учитывая тождества
∂F
∂p
/
∂F
∂ρ
= −
∂ρ
∂p
;
∂F
∂h
/
∂F
∂ρ
= −
∂ρ
∂h
;
∂F
∂c
1
/
∂F
∂ρ
= −
∂ρ
∂c
1
321
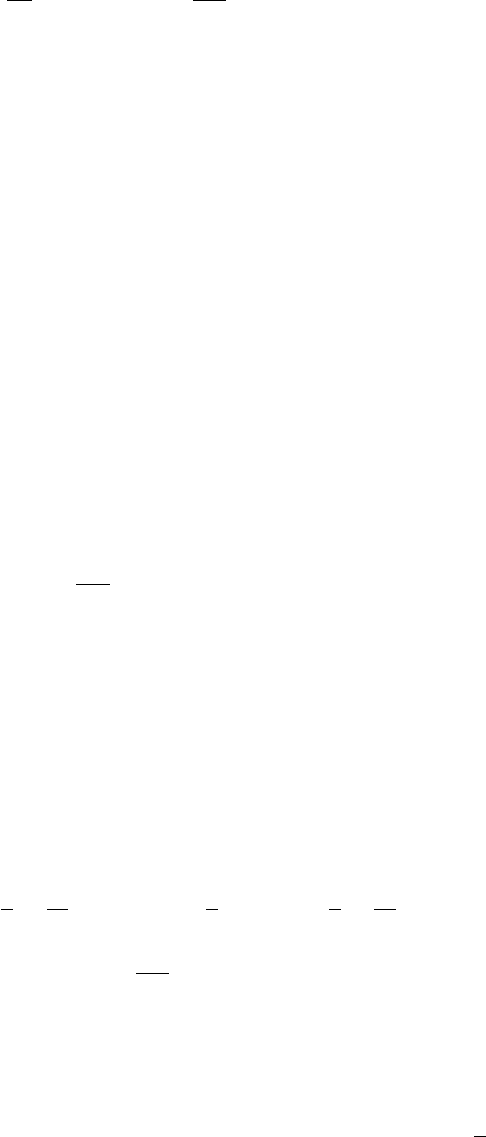
и, привлекая (30), получим уравнение для градиента плотности
dρ
dx
=
1 − M
2
f
−1
∂ρ
∂c
1
ε
1
. (32)
Если подставить (32) в (30), то эту систему дифференциальных уравнений дви-
жения приведем к нормальному виду. При этом система будет автономной.
Замечание 2. Нетрудно заметить, что соотношения на УВ, параметры потока в
зоне индукции и на поверхности воспламенения, а также уравнения движения в зоне
горения содержат неизвестный параметр — скорость волны. Поэтому количествен-
ный расчет структуры детонационной волны возможен лишь после решения главной
задачи — вывода уравнений, определяющих эту скорость.
5. Вывод уравнений, определяющих скорость детонации, связан с особенностями
структуры волны. Напомним, что в результате исследования стационарной детонации
с примыкающей к нейволной разрежения установлено [9, 10], что передний фронт
волны разрежения гладко сшивается со стационарной зоной горения на критической
поверхности (КП), где местное число Маха, рассчитанное по замороженной скоро-
сти звука, равно единице. Поэтому, всоответствии с критериями Гриба-Кирквуда-
Вуда, далееисследуется модель детонации, содержащая в зоне неравновесного го-
рения (ε
1
> 0) КП. В соответствии с Замечанием 1 и из (32) следует, что на КП
выполняются условия
M
2
f
=1, (33)
∂ρ
∂c
1
p,h
=0. (34)
Условие (34) будем называть условием экстремального состояния среды. Так-
как на УВ поток дозвуковой по отношению к замороженной скорости звука, то вся
область течения между УВ и КП является дозвуковой (M
f
< 1). Заметим, что урав-
нения количества движения и энергии в (30) допускают первые интегралы, которые
с учетом (31) и (26) можно представитьв форме, справедливой всюду за УВ. Объеди-
няя эти интегральные соотношения, уравнения состояния (25) и условия (33), (34),
получим замкнутую систему уравнений для параметров потока на КП и скорости
детонации
p − p
0
= −K
2
1
ρ
−
1
ρ
0
; h − h
0
=
1
2
(p − p
0
)
1
ρ
+
1
ρ
0
;
F (h, p, ρ, c
1
)=0;
∂ρ
∂c
1
=0;M
2
f
=1.
(35)
Заметим, чтоуравнения (35) не содержат информации о структуре волны и меха-
низмах реакции за УВ. Это означает, что скорость детонации является константой
исходной горючей смеси. Дадим геометрическую интерпретацию уравнениям (35),
предварительно опустив в этой системе условие (33). Тогда в плоскости
1
ρ
,p
пер-
322
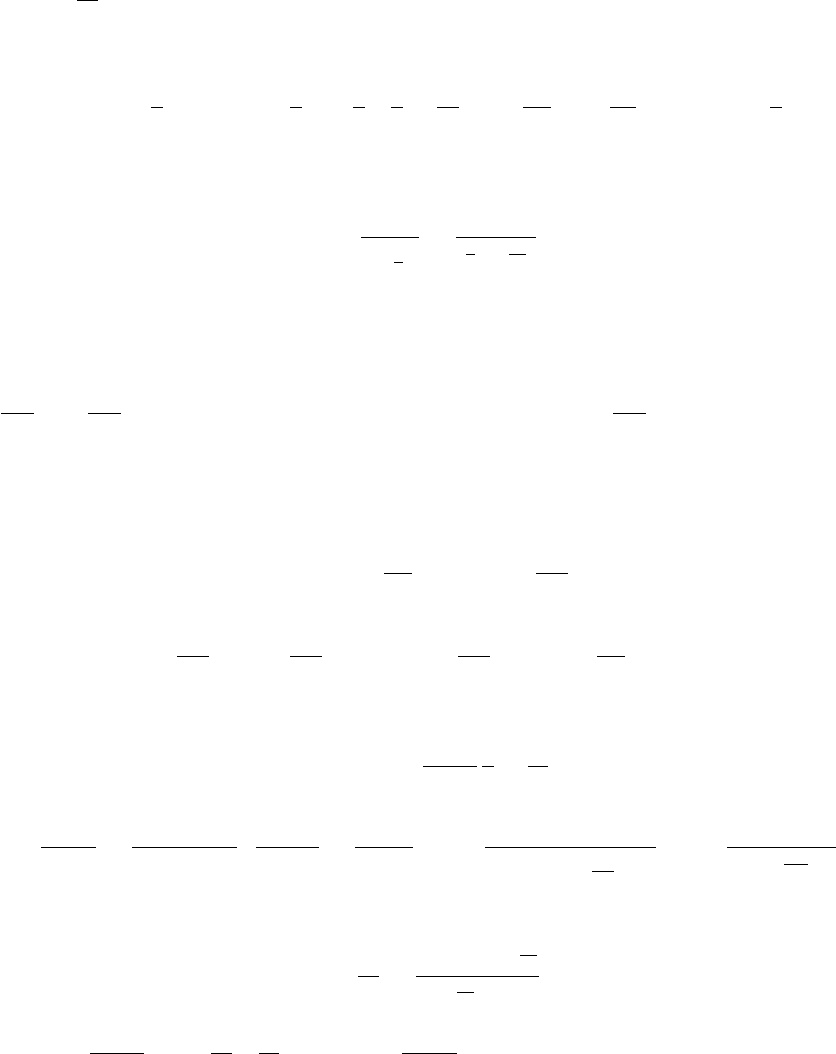
вое уравнение определяет прямую Михельсона, проходящую через начальное состо-
яние
1
ρ
0
,p
0
а остальные — адиабату экстремальных состояний (а.э.с.). Запишем
второе и третье уравнения (35) в дифференциалах с учетом (34)
dh =
1
2
(p − p
0
) d
1
ρ
+
1
2
1
ρ
−
1
ρ
0
dp;
∂ρ
∂h
dh +
∂ρ
∂p
dp = −ρ
2
d
1
ρ
.
Исключая из этих равенств dh, а затем, используя условие касания прямой Михель-
сона к а.э.с.
dp
d
1
ρ
=
(p − p
0
)
1
ρ
−
1
ρ
0
,
получим соотношение (33). Иначе говоря, детонация распространяется в режиме
Чепмена-Жуге, но по отношению к этой адиабате.
Приведем теперь явный вид а.э.с. для смеси политропных газов. Из равенства
∂c
1
∂ρ
=
∂ρ
∂c
1
−1
следует, чтов экстремальном состоянии
∂c
1
∂ρ
= ∞. Решая уравнение
(25) относительно c
1
, получим (23). Из вида (23) следует, чтов экстремальном со-
стоянии дискриминант уравнения равен нулю (D
0
=0). После преобразований его
можно записать так
Ψ=
L
1
−
Q
1
Q
2
L
2
L
2
−
M
2
M
1
L
2
Ψ+
+
b
M
2
L
1
−
M
2
M
1
L
2
+ Q
2
b
b
M
2
−
L
1
−
Q
1
Q
2
L
2
=0.
Возвращаясь к истинным переменным, из этого равенства получим
h + q
0
=
γ
γ − 1
p
ρ
−
z
2
z
1
q
2
, (36)
где
γ
γ − 1
=
γ
0
(γ
0
− 1) z
1
;
γ
0
− 1
γ
0
=
R
m
0
c
p0
; z
1
=
b
M
2
L
1
−
Q
1
Q
2
L
2
; z
2
=
b (z
1
− 1)
L
1
−
M
2
M
1
L
2
.Объ-
единим (36) и второе уравнение в (35). Исключая из них b, получим уравнение
а.э.с.
p
p
0
=
2α +æ−
ρ
0
ρ
æ
ρ
0
ρ
− 1
, (37)
где æ=
γ +1
γ − 1
; α =
ρ
0
ρ
z
2
z
1
q
2
+ h
0
−
γ
γ − 1
.
Нетрудно заметить, что уравнение а.э.с. (37) с точностью до обозначений сов-
падает с уравнением детонационной адиабаты в классической теории Михельсона-
Чепмена-Жуге. Поэтому в рамках излагаемой теории скорость потока и параметры
потока на КП вычисляются по формулам классической теории. Этот удивительный
323
