Шемякин Е.И., Смирнов Н.Н., Нигматулин Р.И., Натяганов В.Л. (редакторы) Газовая и волновая динамика

Подождите немного. Документ загружается.

Уравнение Стокса с силовой функцией от стресслета и квадруполя совместно с

(20) и (21) дают аналог системы (16) для деформационно-сдвигового потока. Путем

осреднения этой системы по ансамблю возможных конфигураций [7 – 10] желатель-

но проверить полученное в [11, 12] методом самосогласованного поля или стандарт-

ной процедурой подсчета мощности диссипации энергии [2, 19] обобщение формулы

Эйнштейна-Тейлора для эффективной вязкости

∗

= µ



˜σ(5˜µ +2)+q

(2˜σ +3)

5˜σ(˜µ +1)+q

(2˜σ +3)



. (22)

с поверхностным зарядом ДЭС в деформационно-сдвиговом потоке.

Заметим, что около капли во внешнем электрическом поле, находящейся вбли-

зи точки максимума электрокапиллярной кривой [20], будет генерироваться ЭГД-

течение с электрическим потенциалом вида (14), по функцией тока вида (17), что

приводит к еще одной модификации системы типа (16). Подчеркнем, что аналогич-

ная система, но со своими коэффициентами, получается при ЭГД-обтекании капли

с ПС зарядов [18], так что и формулы для µ

∗

в этих двух случаях должны иметь

отличную от (22), но похожую структуру. Аналогичным образом выражение для µ

∗

при электрокапиллярном движении суспензии при q = const должно быть другим,

относительно чего в литературе существуют разночтения, однако получение формул

в этих случаях - тема отдельного исследования.

Работа выполнена по гранту РФФИ (№ 01-01-00010)

Литература

[1] Владимиров В. С. Обобщенные функции в математической физике. — М.:

Наука, 1979.

[2] Хаппель Дж., Бреннер Г. Гидродинамика при малых числах Рейнольдса. —

М.: Мир, 1976.

[3] Головин А. М., Натяганов В. Л. Магнитогидродинамическое обтекание капли

при малых числах Рейнольдса и Гартмана. — МЖГ, 1978, № 6.

[4] Натяганов В. Л. Магнитогидродинамическое обтекание вращающегося шара

при малых числах Рейнольдса и Гартмана в приближении Озеена. — Вест.

МГУ, сер. 1, 1980, № 3.

[5] Chwang A. T., Wu T. Y. Hydromechanics of low-Reynolds-number flow. — J.

Fluid Mech., pt. 1: 1974, v. 63; pt. 2: 1975, v. 67.

[6] Новое в зарубежной науке. — Сер. Механика, № 22, 1980, М. Мир, 1980.

[7] Головин А. М., Чижов В. Е. К расчету скорости осаждения однородной сус-

пензии. — ПММ, 1978, т. 42, № 1.

[8] Головин А. М., Чижов В. Е. Об эффективной теплопроводности суспензии. —

Вест. МГУ, сер. 1, 1978, № 1.

334

[9] Натяганов В. Л. Электрические свойства однородных суспензий сферических

частиц. — Сб. Современные проблемы механики и прикладной математики, ч.

2, Воронеж, ВГУ, 2000.

[10] Натяганов В. Л., Орешина И. В. Электрогидродинамика монодисперсных

эмульсий, ч. 1, 2. — Колл. жур., 2000, т. 62, № 1.

[11] Натяганов В. Л., Орешина И. В., Чайка А. А. Эффективные гидродинами-

ческие и электрические характеристики однородных суспензий сферических

частиц. — Сб. «Математика. Компьютер. Образование.», вып. 8, М: Прогресс-

Традиция, 2001.

[12] Натяганов В. Л. Сингулярный метод в моделях электрогидродинамики сус-

пензий. — Сб. Упругость и не упругость, М.: Изд-во МГУ, 2001.

[13] Натяганов В. Л. Электрокапиллярновихревая модель шаровой молнии. Эф-

фект гигантской диэлектрической проницаемости суспензии. — Аннотации до-

кладов VIII Всероссийского съезда по теоретической и прикладной механике,

Пермь, 2001.

[14] Натяганов В. Л. Электровихревая модель электрокапиллярного движения

сферической капли и шаровой молнии. Эффект гигантской электрической про-

ницаемости однородной суспензии. — Сб. науч. трудов «Математика. Компью-

тер. Образование.», вып. 8, ч. II, М.: Прогресс-Традиция, 2001.

[15] Натяганов В. Л. Электрокапиллярновихревая модель сферического вихря

Хилла-Тейлора. — ДАН, 2001, т. 381, № 1.

[16] Левич В. Г. Физико-химическая гидродинамика. — М.: Физматгиз, 1959.

[17] Мелчер Дж. Р. Электрогидродинамика. — МГ, 1974, № 2.

[18] Мелчер Дж. Р., Тейлор Дж. Электрогидродинамика: обзор роли межфазных

касательных напряжений. — Механика, сб. переводов, 1971, № 5.

[19] Бэтчелор Дж. Введение в динамику жидкости. — М.: Мир, 1973.

[20] Натяганов В. Л. Некоторые особенности электрокапиллярного движения ка-

пель. — Сб. Механика деформируемых сред, М.: Изд-во МГУ, 1985.

335

Перемешивание при вытеснении вязких жидкостей из

ячейки Хеле-Шоу

Ивашнев О. Е., Шахмардан М. М.

1. Введение

Ячейка Хеле-Шоу служит физической моделью пористой среды. Она представляет

собой канал, образованный двумя параллельными пластинами, расположенными на

расстоянии δ значительно меньшем длины L и ширины канала H. Фронт вытесне-

ния вязкой жидкости другой, менее вязкой, неустойчив. Менее вязкая, вытесняющая

жидкость прорывается через слой вытесняемой: образуя в ней каналы: называемые

вязкими пальцами. В результате образуется область (фронт вытеснения) лежащая

между основаниями и вершинами пальцев, в которой находится как вытесняемая,

так и вытесняющая жидкости. Изменение ширины этой области во времени в зави-

симости от параметров течения и требуется рассчитать.

Известно [1], [2], что форма вязких пальцев определяться силами поверхностного

натяжения и диффузией жидкостей. Но при вытеснении нефти водой из пористой

среды оба эти фактора не работают[3]. Нефть не смешивается с водой, и поэтому

диффузии нет. Силы поверхностного натяжения из-за разобщенности капилляров

грунта не зависят от формы фронта и, следовательно, не могут влиять на форму

вязких пальцев. Однако существуют эксперименты, в которых, несмотря на отсут-

ствие этих известных стабилизирующих факторов, вязкие пальцы имеют примерно

одинаковую ширину и похожую форму. На рис. 1 представлены результаты экспе-

риментов [4]. Даны фотографии фронта вытеснения в два момента времени t

=2c

и t

=8c. Вытесняется водоглицериновая смесь (справа) водой (слева) из ячейки

Хеле-Шоу с зазором между пластинами δ =1.2 мм, длиной и шириной 200 и 100

мм. Среднеобъемная скорость вытеснения U =1см/с. Отношение вязкостей вы-

тесняемой и вытесняющей жидкости M = µ

/µ

=84. Видно, что граница между

жидкостями, несмотря на ее сложную форму, не размывается со временем. Следова-

тельно, благодаря высокой скорости вытеснения эффекты диффузии не проявляются

в этом эксперименте. С другой стороны, поскольку вода и глицерин смешивающиеся

жидкости, на их межфазной поверхности не возникает сил поверхностного натяже-

ния. Таким образом, и с этой точки зрения этот эксперимент моделирует процесс

вытеснения нефти водой из пористой среды.

Мы предположили, что малые силы инерции, наряду с другими малыми пара-

метрами (силами поверхностного натяжения, действующими в плоскости течения,

диффузией) определяют размеры вязких пальцев и, следовательно, влияют на эф-

фективный коэффициент диффузии. Для проверки высказанной гипотезы была со-

ставлена математическая модель течения в ячейке Хеле-Шоу учитывающая инерцию

жидкости. Решения, полученные с ее помощью были сопоставлены с данным экспе-

римента.

336

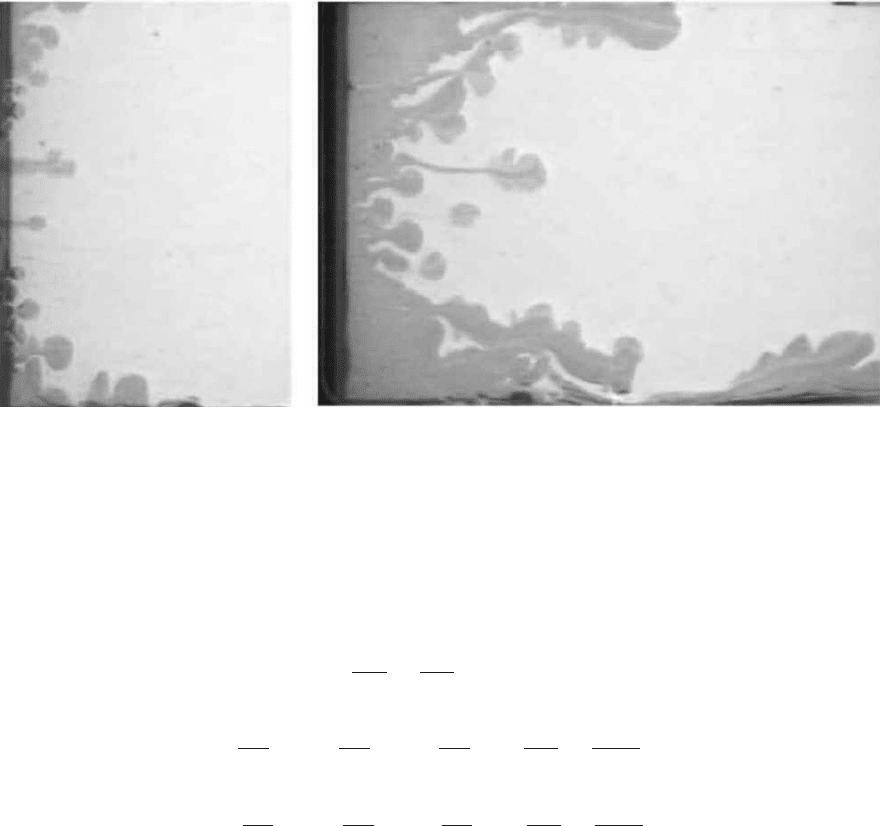
Рис. 1: Фотографии фронта вытеснения вязкой жидкости из ячейки Хеле-Шоу

(δ =1.2 мм, U =1см/с, M =84).

2. Математическая модель

Движение обеих жидкостей описывается одними и теми же уравнениями:

∂u

∂x

∂v

∂y

=0 , (1)

∂u

∂t

+ ρ

∂u

∂x

+ ρ

∂u

∂y

= −

∂P

∂x

−

12 µ

u, (2)

∂v

∂t

+ ρ

∂v

∂x

+ ρ

∂v

∂y

= −

∂P

∂y

−

12 µ

v (3)

где i =1для параметров, относящихся к вытесняющей жидкости; i =2— вытесня-

емой.

На межфазной поверхности ставится условие равенства давлений и нормальных

к межфазной поверхности составляющих векторов скорости жидкостей:

x = ξ (t, y): P

= P

= Pw

= w

(4)

3. Результаты анализа роста малых возмущений плоской меж-

фазной поверхности

Рассматривается эволюция малого синусоидального возмущения



= exp [i (ωt− y/λ)] (5)

337

межфазной поверхности, находящейся на линии x =0. Первый постоянный пара-

метр решения (5) — комплексная частота, является мнимым; второй, длина волны

возмущения — действительным. Предполагаем, что амплитуда возмущений затухает

при удалении от поверхности фронта:

x →±∞: P



→ 0 (6)

Для случая, когда плотности вытесняемой и вытесняющей жидкостей равныρ

= ρ, связь между постоянными параметрами решения (5) имеет вид:



1,2

⎡

⎣

3(1+M)

MRe



6(M − 1)

MRe

9(1+M)

⎤

⎦

i, (7)

где i

= −1

 =

ωδ

λ =

> 1 Re =

ρδU

безразмерные комплексная частота, длина волны и число Рейнольдса. Для рассмат-

риваемого течения (рис. 1) Re =0.14.

Из (5), (7) видно, что каждой длине волны λ соответствуют два значения .

Первое имеет положительную мнимую часть. Оно дает затухание возмущения. Вто-

рое с отрицательной мнимой частью дает его рост. На рис. 2 показана зависимость

отрицательной мнимой части 

(декремента затухания) от длины. Часть кривой,

лежащая левее линии

λ =1не имеет физического смысла. На этом участке не вы-

полняется допущение модели о малости ширины ячейки в сравнении с линейными

размерами течения.

Из рисунка видно, что наибольшая интенсивность роста наблюдается у

возмущений наименьшей длины волны. Таким образом, если плоский фронт воз-

мущен случайным образом, то с наибольшей интенсивностью будут расти самые

короткие возмущения.

4. Задача об одиночном вязком пальце в ячейке Хеле-Шоу

В этой задаче рассматривается другой предельный случай, анализируется рост воз-

мущений имеющих бесконечную длину. В ячейке Хеле-Шоу шириной h со скоро-

стью U

распространяется вязкий палец (рис. 3). Скорость жидкости, при x →∞—

U<U

. Требуется рассчитать ширину вязкого пальца λ.

Из уравнения неразрывности следует связь между скоростью пальца и жидкости

на удалении от него:

λ + U

(h − λ)=Uh. (8)

где U

— скорость жидкости при x →−∞, т.е. жидкости движущейся вдоль плоских

стенок пальца. Из предположения о существовании плоских стенок следует вывод об

338

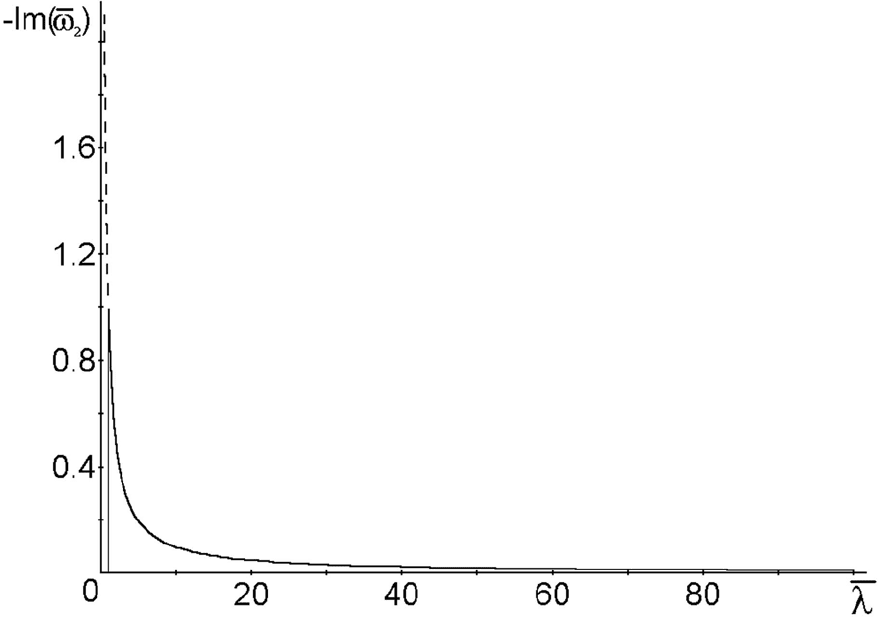
Рис. 2: Зависимость декремента затухания, взятого со знаком минус, от длины

волны (Re =0.14, M =84).

339

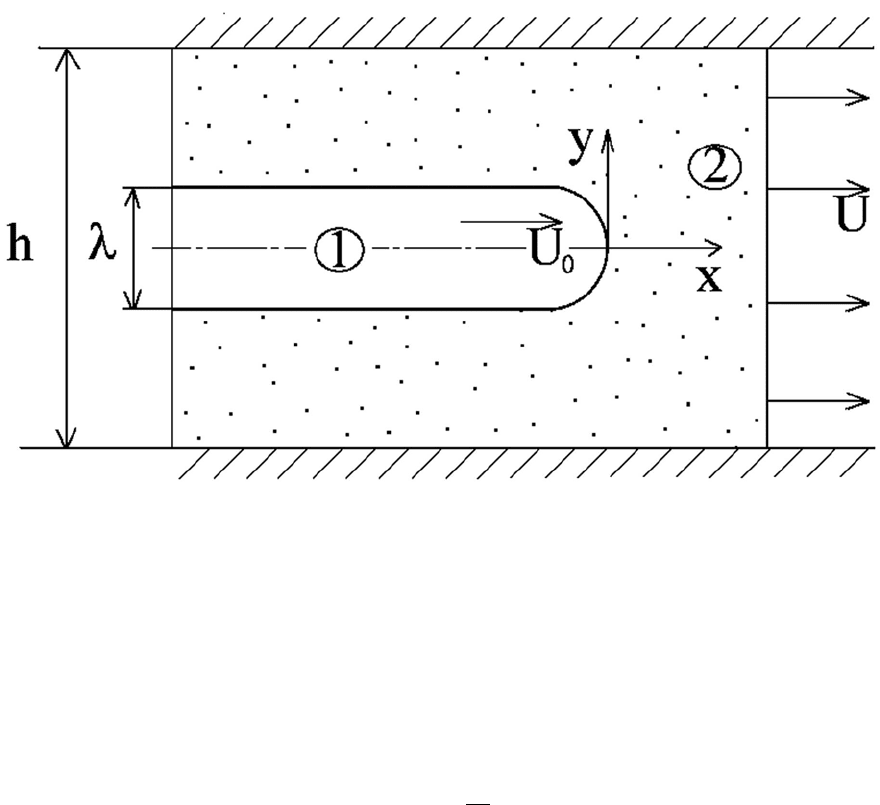
Рис. 3: Постановка задачи о бесконечно длинном вязком пальце в ячейке.

однородности давления в сечении y = const. Приравнивая давления в вытесняющей

и вытесняемой жидкости, получаем:

= µ

(9)

Из уравнений (8), (9) получаем:



λ +(h − λ)



= Uh. (10)

Уравнение (10), полученное из общих интегральных соотношений, дает связь

между неизвестными параметрами задачи U

и λ. Оказалось, что решение задачи

о вязком пальце в классической постановке [5], которое строится без учета сил

инерции, не дает второй связи между этими параметрами. В соответствии с этим

решением она может быть любой [6]. Путем подбора источников и стоков, располо-

женных на оси симметрии течения (рис. 3) было получено приближенное решение

задачи о вязком пальце с учетом сил инерции. Малые силы инерции доминируют в

особой точке потока x = y =0(рис. 3). Из условия существования решения в этой

точке следует соотношение между интенсивностью лобового источника и скоростью

потока. Это соотношение, в неявной форме (в которую входят интенсивности многих

источников и их координаты) дает недостающую связь между параметрами U

и λ.

Таким образом, из решения задач об эволюции малых возмущений плоской по-

верхности и о вязком пальце следует, что на межфазной поверхности вначале вы-

растают узкие пальцы, шириной ∼ δ. По мере роста ширина их возрастает. Это

340

объясняет необычную «грушевидную» форму вязких пальцев наблюдаемых в экспе-

рименте, представленном на рис. 1.

5. Результаты численного моделирования

Чтобы проследить за эволюцией вязких пальцев и рассчитать интегральную харак-

теристику процесса вытеснения — эффективный коэффициент диффузии, задача о

вытеснении вязкой жидкости была решена численно. В основу алгоритма было по-

ложено предположение о существовании непрерывного поля скоростей и давлений

около межфазной поверхности. Тогда, используя тот факт, что параметры, опреде-

ляемые физическими свойствами жидкостей ρ

и µ

, входят в систему уравнений

(1) – (3) лишь в виде коэффициентов, возможно рассчитать поле скоростей и давле-

ний для каждого последующего момента времени во всей области течения. Затем, по

известному полю скоростей, определялось новое положение межфазной поверхности.

Поскольку уравнения (2), (3) являются уравнениями типа Эйлера (они не со-

держат второй производной от скорости), на межфазной поверхности может быть

выполнено лишь условие равенства нормальных к поверхности составляющих скоро-

сти. Касательные же составляющие могут терпеть разрыв. Поэтому предположение о

непрерывности параметров у межфазной поверхности не следует из математической

постановки задачи. Однако, известно [7], что численный аналог уравнений отличает-

ся от математического. Численная схема «добавляет» к математическим уравнениям

старшие производные. Поэтому в численных расчетах по сути решаеся полная систе-

ма уравнений типа Навье-Стокса, в которой схемная вязкость подобрана так, чтобы

размазать скачок скорости на 1–2ячейки(взависимости от типа схемы).

Из-за трудности моделирования течения вокруг десятков вязких пальцев одно-

временно, в численном эксперименте было рассмотрено течение только в 1/10 части

экспериментальной ячейки Хеле-Шоу. На рис. 4,а показана форма фронта вытесне-

ния в несколько моментов времени, рассчитанная для «неинерциальной» жидкости

(Re =0). За единицу измерения времени принято время прохождения жидкой части-

цы, движущейся со среднемассовой скоростью U, расстояния равного ширине ячейки

Хеле-Шоу используемой в численном эксперименте T

∗

= U t/h (h =0.1 H). Видно,

что в безинерционной жидкости ширина вязких пальцев не изменяется в процессе

их эволюции. Она остается минимально возможной и равной нескольким ячейкам

численной сетки.

В инерционной жидкости (рис. 4, б) вязкие пальцы постепенно утолщаются, а

жидкий «мост» отделяющий их головную часть от основной массы вытесняющей

жидкости, наоборот, утончается. Аналогичные конфигурации наблюдаются и в экс-

перименте (рис. 1). В целом, численный эксперимент подтвердил существенную роль

инерции жидкости в процессе формирования структуры фронта вытеснения при вы-

бранных параметрах течения.

341

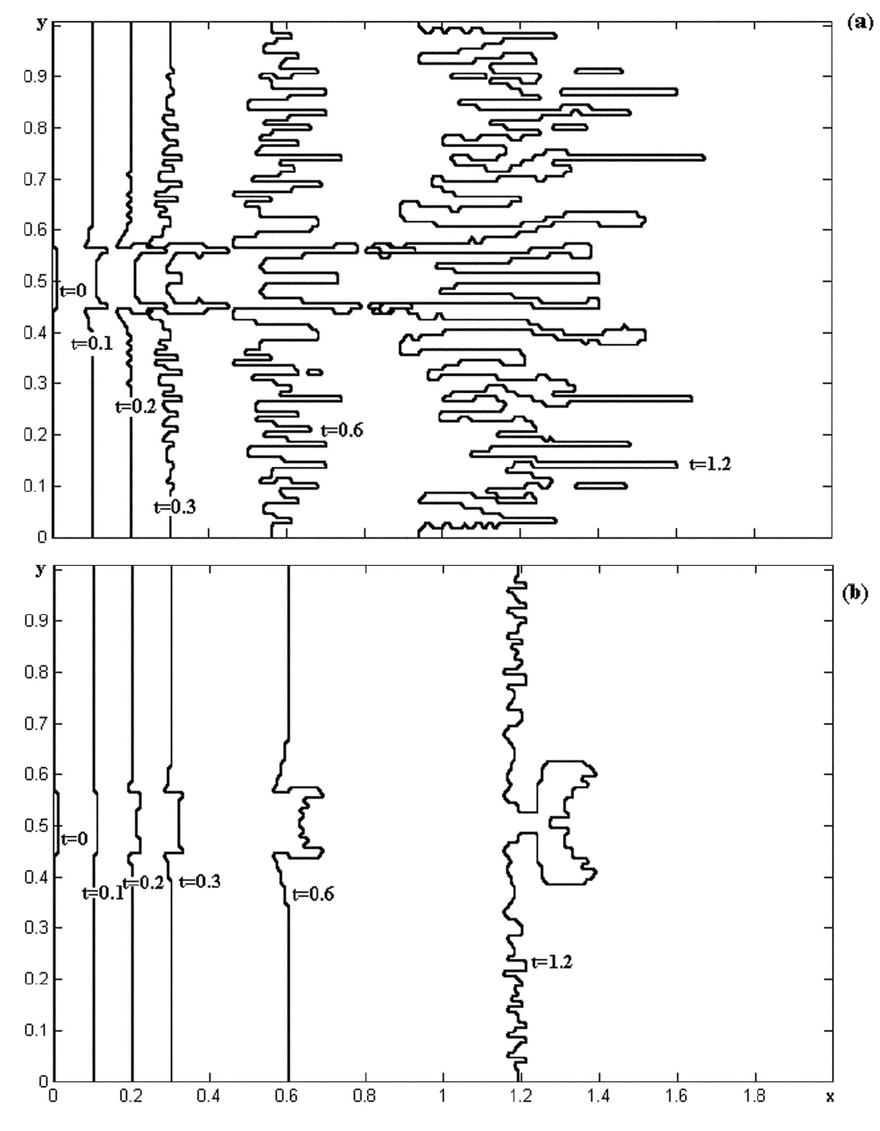
Рис. 4: Структура фронта вытеснения в численном эксперименте: а — в неинер-

ционной жидкости; б—сучетоминерции.

342

6. Заключение

Анализ устойчивости на малые возмущения первоначально плоского фронта вытес-

нения вязкой жидкости другой, менее вязкой показал, что с наибольшей скоростью

растут наиболее короткие возмущения, длиной порядка ширины ячейки Хеле-Шоу.

Таким образом, возникающие пальцы имеют ширину ∼ δ.

Решение задачи о вязком пальце в ячейке Хеле-Шоу с учетом инерции жидкости

позволяет рассчитать ширину вязкого пальца. Из решения двух аналитических задач

следует, что ширина вязкого пальца по мере его роста увеличивается, стремясь к

стационарному значению.

Численные расчеты процесса неустойчивого вытеснения подтвердили вывод ли-

нейного анализа о доминирующем росте коротких возмущений. Все образующие

пальцы имеют минимально возможную ширину. В расчетах без учета инерции жид-

кости ширина вязкого пальца не меняется со временем. При учете инерции шири-

на вязких пальцев увеличивается по мере их роста. Это находится в соответствии

с данными эксперимента и подтверждает роль инерции в процессе формирования

структуры фронта неустойчивого вытеснения.

Литература

[1] Park C.W., Homsy G.M. The instability of long fingers in Hele-Show flows. —

Phys. Fluids 1985, V.28, N. 6.

[2] Homsy G.M. Viscous fingering in porous media. — Ann. Rev. Fluid Mech., 1987,

V.19.

[3] Smirnov N.N., Nikitin V.F., Ivashnyov O.E., Legros J.C., Vedernikov A., Scheid

B., Istasse E. Instability in viscous fluids displacement from cracks and porous

samples. — Proc. 53-d Internat. Astronautical Congress, Houston 2002, IAC-02-

J.2.02.

[4] Smirnov N.N., Nikitin V.F., Ivashnyov O.E., Maximenko A., Thiercelin M.,

Vedernikov A., Scheid B., Istasse E, Legros J.C. Theoretical and experimental

study of instability and the mixing flux in frontal displacement of fluids. — Proc.

54-d Internat. Astronautical Congress, Bremen 2003, IAC-03-J.2.03.

[5] Saffman P.G., Taylor G.J. The penetration of a fluid into a porous medium of

Hele-Show cell containing a more viscous fluid. — Proc. R. Foc. Zond., A 245,

312, 1958.

[6] Tanveer S. Surprises in viscous fingering. — J. Fluid Mech., 2000, V. 409.

[7] Роуч П. Вычислительная гидродинамика. — М.: Мир, 1980.

343