Шапкин А.С., Шапкин В.А. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями
Подождите немного. Документ загружается.


41
Óãëîâîé êîýôôèöèåíò k ïðÿìîé, çàäàííîé äâóìÿ òî÷êàìè
À(x
A
; y
A
) è B(x
B
; y
B
), âû÷èñëÿåòñÿ ïî ôîðìóëå
.
BA
BA
AB
xx
y
y
k
−
−
=
(1.26)
Óðàâíåíèåì ïðÿìîé â îòðåçêàõ íàçûâàåòñÿ óðàâíåíèå âèäà:
,1=+
b
y
a
x
(1.27)
ãäå à è b ñîîòâåòñòâåííî àáñöèññà è îðäèíàòà òî÷åê ïåðå-
ñå÷åíèÿ ïðÿìîé ñ îñÿìè Îõ è Îy, ò.å. äëèíû îòðåçêîâ, îòñåêà-
åìûõ ïðÿìîé íà êîîðäèíàòíûõ îñÿõ, âçÿòûå ñ îïðåäåëåííûìè
çíàêàìè.
Óðàâíåíèå ïðÿìîé, ïðîõîäÿùåé ÷åðåç òî÷êó À(x
A
; y
A
) è èìåþ-
ùåé óãëîâîé êîýôôèöèåíò k, çàïèñûâàåòñÿ â âèäå:
y y
A
= k (x x
A
). (1.28)
Ïó÷êîì ïðÿìûõ íàçûâàåòñÿ ñîâîêóïíîñòü ïðÿìûõ ïëîñêîñòè,
ïðîõîäÿùèõ ÷åðåç îäíó è òó æå òî÷êó À öåíòð ïó÷êà. Óðàâíå-
íèå (1.28) ìîæíî ðàññìàòðèâàòü êàê óðàâíåíèå ïó÷êà ïðÿìûõ,
ïîñêîëüêó ëþáàÿ ïðÿìàÿ ïó÷êà ìîæåò áûòü ïîëó÷åíû èç óðàâíå-
íèÿ (1) ïðè ñîîòâåòñòâóþùåì çíà÷åíèè óãëîâîãî êîýôôèöèåíòà k.
Èñêëþ÷åíèå ñîñòàâëÿåò ëèøü îäíà ïðÿìàÿ ïó÷êà, êîòîðàÿ ïàðàë-
ëåëüíà îñè Îy åå óðàâíåíèå õ = x
A
.
Óðàâíåíèå ïðÿìîé, ïðîõîäÿùåé ÷åðåç äâå äàííûå òî÷êè
À(x
A
; y
A
) è B(x
B
; y
B
), èìååò âèä:
.
AB
A
AB
A
y
y
y
y
xx
xx
−
−
=
−
−
(1.29)
Åñëè òî÷êè A è B îïðåäåëÿþò ïðÿìóþ, ïàðàëëåëüíóþ îñè
Îõ (y
A
= y
B
) èëè îñè Îy (x
A
= õ
B
), òî óðàâíåíèå òàêîé ïðÿìîé çà-
ïèñûâàåòñÿ ñîîòâåòñòâåííî â âèäå:
y = y
A
èëè x
= õ
A
. (1.30)

42
Óñëîâèÿ ïåðåñå÷åíèÿ, ïàðàëëåëüíîñòè èëè ñîâïàäåíèÿ äâóõ
ïðÿìûõ, çàäàííûìè ñâîèìè îáùèìè óðàâíåíèÿìè
A
1
x + B
1
y + C
1
= 0 è A
2
x + B
2
y + C
2
= 0,
ïðèâåäåíû â ñëåäóþùåé òàáëèöå.
.Ñîâïàäåíèå
.îñòüÏàðàëëåëüí
.åÏåðåñå÷åíè
ëîâèå Óñ
ïðÿìûõ èåðàñïîëîæåí
Âçàèìíîå
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
C
C
B
B
A
À
C
C
B
B
A
À
B
B
A
À
==
≠=
≠
(1.31)
Åñëè èçâåñòíû óãëîâûå êîýôôèöèåíòû k
1
è k
2
ïðÿìûõ, òî óñ-
ëîâèå ïàðàëëåëüíîñòè ýòèõ ïðÿìûõ ñîñòîèò â ðàâåíñòâå èõ óãëî-
âûõ êîýôôèöèåíòîâ: k
1
= k
2
.
Óñëîâèå ïåðïåíäèêóëÿðíîñòè äâóõ ïðÿìûõ, óãëîâûå êîýôôè-
öèåíòû êîòîðûõ ñîîòâåòñòâåííî ðàâíû k
1
è k
2
, ñîñòîèò â âûïîë-
íåíèè ñîîòíîøåíèÿ
k
1
k
2
+ 1 = 0
èëè
,
1
2
1
k
k −=
(1.32)
ò.å. óãëîâûå êîýôôèöèåíòû ýòèõ ïðÿìûõ îáðàòíû ïî àáñîëþòíîé
âåëè÷èíå è ïðîòèâîïîëîæíû ïî çíàêó.
Ïîä óãëîì ìåæäó äâóìÿ ïðÿìûìè ïîíèìàåòñÿ îäèí èç äâóõ
ñìåæíûõ óãëîâ, îáðàçîâàííûõ ïðè èõ ïåðåñå÷åíèè. Òàíãåíñ óãëà
ϕ
ìåæäó äâóìÿ ïðÿìûìè, óãëîâûå êîýôôèöèåíòû êîòîðûõ ñîîòâåò-
ñòâåííî ðàâíû k
1
è k
2
, âû÷èñëÿåòñÿ ïî ôîðìóëå
,
1
tg
21
12
kk
kk
+
−
±=
ϕ
(1.33)
ïðè÷åì çíàê «ïëþñ» ñîîòâåòñòâóåò îñòðîìó óãëó
ϕ
, à çíàê
«ìèíóñ» òóïîìó.

43
Óðàâíåíèå îêðóæíîñòè ñ öåíòðîì â òî÷êå S(a; b) è ðàäèóñîì r
èìååì âèä:
(x a)
2
+ (y b)
2
= r
2
. (1.34)
Ýòî êàíîíè÷åñêîå óðàâíåíèå îêðóæíîñòè (ðèñ. 7).
Óðàâíåíèå âòîðîé ñòåïåíè îòíîñèòåëüíî òåêóùèõ êîîðäèíàò
õ è ó ÿâëÿåòñÿ óðàâíåíèåì îêðóæíîñòè òîãäà è òîëüêî òîãäà, êîã-
äà â ýòîì óðàâíåíèè êîýôôèöèåíòû ïðè êâàäðàòàõ êîîðäèíàò ðàâ-
íû, à ÷ëåí ñ ïðîèçâåäåíèåì êîîðäèíàò îòñóòñòâóåò. Òàêèì îáðà-
çîì, ýòî óðàâíåíèå èìååò âèä:
Ax
2
+ Ây
2
+ Cx + Dy + F = 0. (1.35)
 ýòîì ñëó÷àå ãîâîðÿò, ÷òî îêðóæíîñòü çàäàíà îáùèì óðàâíå-
íèåì.
Äëÿ îïðåäåëåíèÿ êîîðäèíàò öåíòðà è ðàäèóñà îêðóæíîñòè,
çàäàííîé îáùèì óðàâíåíèåì, íàäî ñ ïîìîùüþ òîæäåñòâåííûõ ïðå-
îáðàçîâàíèé óðàâíåíèå (1.35) ïðèâåñòè ê âèäó (1.34).
Ýëëèïñ åñòü ãåîìåòðè÷åñêîå ìåñòî òî÷åê, ñóììà ðàññòîÿíèé
êîòîðûõ îò äâóõ ôèêñèðîâàííûõ òî÷åê, íàçûâàåìûõ ôîêóñàìè
ýëëèïñà, åñòü âåëè÷èíà ïîñòîÿííàÿ (2à), áîëüøàÿ, ÷åì ðàññòîÿíèå
ìåæäó ôîêóñàìè (2ñ).
Ïðîñòåéøåå óðàâíåíèå ýëëèïñà ïîëó÷àåòñÿ, åñëè ðàñïîëîæèòü
êîîðäèíàòíóþ ñèñòåìó ñëåäóþùèì îáðàçîì: çà îñü Îx ïðèíÿòü
ïðÿìóþ, ïðîõîäÿùóþ ÷åðåç ôîêóñû F
1
è F
2
, à çà îñü Îó ïåðïåí-
Ðèñ. 7
S(a; b)
0
r
x
y
•
44
äèêóëÿð ê îñè àáñöèññ â ñåðåäèíå îòðåçêà F
1
F
2
(ðèñ. 8). Òîãäà óðàâ-
íåíèå ýëëèïñà ïðèìåò âèä:
,1
2
2
2
2
=+
b
y
a
x
(1.36)
ãäå b
2
= a
2
c
2
.
Òî÷êè À
1
è À
2
, B
1
è B
2
ïåðåñå÷åíèÿ ýëëèïñà ñ åãî îñÿìè ñèì-
ìåòðèè (êîîðäèíàòíûìè îñÿìè) íàçûâàþòñÿ âåðøèíàìè ýëëèïñà.
Îòðåçêè À
1
À
2
= 2à è B
1
B
2
= 2b íàçûâàþòñÿ îñÿìè ýëëèïñà, ïðè÷åì
À
1
À
2
áîëüøîé îñüþ, à B
1
B
2
ìàëîé îñüþ, òàê êàê a > b. Òàêèì
îáðàçîì, ïàðàìåòðû a è b, âõîäÿùèå â óðàâíåíèå ýëëèïñà, ðàâíû
åãî ïîëóîñÿì.
Ýêñöåíòðèñèòåòîì ýëëèïñà íàçûâàåòñÿ îòíîøåíèå ðàññòîÿíèÿ
ìåæäó ôîêóñàìè ê åãî áîëüøîé îñè, ò.å.
.
a
c
e =
(1.37)
Î÷åâèäíî, ÷òî å < 1.
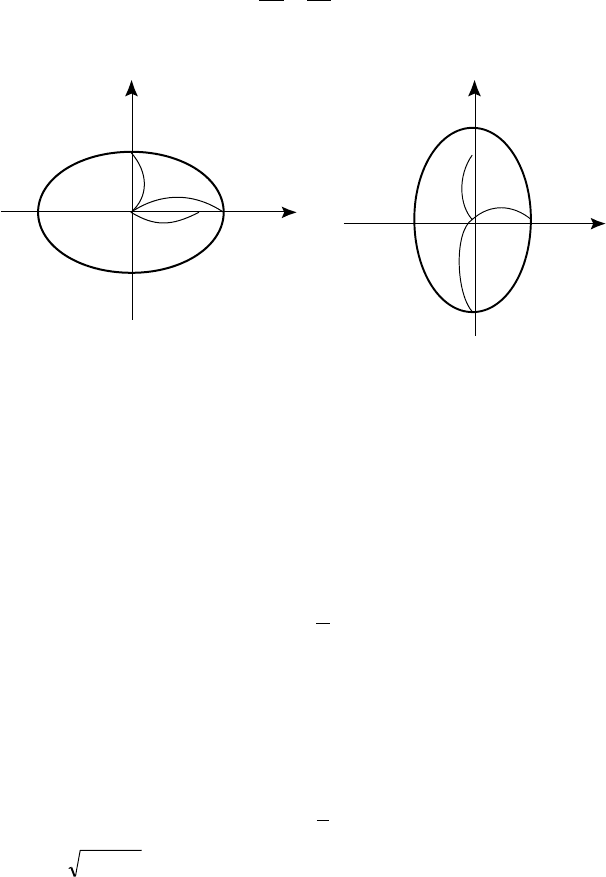
Åñëè ýëëèïñ, îïðåäåëÿåìûé óðàâíåíèåì âèäà (1.36), ðàñïîëî-
æåí òàê, ÷òî åãî ôîêóñû ëåæàò íà îñè Îó (ðèñ. 9), òî òîãäà b > à è
óæå áîëüøîé îñüþ áóäåò îòðåçîê B
1
B
2
= 2b, à ìàëîé îñüþ îòðå-
çîê À
1
À
2
= 2à. Ýêñöåíòðèñèòåò òàêîãî ýëëèïñà âû÷èñëÿåòñÿ ïî
ôîðìóëå
,
b
c
e =
(1.38)
ãäå
.
22
abc −=
Ðèñ. 8
0
a
x
y
•
•
•
b
c
A
1
A
2
B
1
F
1 F
2
•
•
Ðèñ. 9
0
a
x
y
•
•
•
b
c
A
1
A
2
B
1
B
2
F
1
F
2
•
•
•
B
2

45
Ãèïåðáîëîé íàçûâàåòñÿ ãåîìåòðè÷åñêîå ìåñòî òî÷åê, àáñîëþò-
íàÿ âåëè÷èíà ðàçíîñòè ðàññòîÿíèé êîòîðûõ îò äâóõ äàííûõ òî-
÷åê, íàçûâàåìûõ ôîêóñàìè, åñòü âåëè÷èíà ïîñòîÿííàÿ (2à), ìåíü-
øàÿ, ÷åì ðàññòîÿíèå ìåæäó ôîêóñàìè (2ñ).
Ïðîñòåéøåå óðàâíåíèå ãèïåðáîëû ïîëó÷àåòñÿ, åñëè ðàñïîëî-
æèòü êîîðäèíàòíóþ ñèñòåìó ñëåäóþùèì îáðàçîì: çà îñü Îõ ïðè-
íÿòü ïðÿìóþ, ïðîõîäÿùóþ ÷åðåç ôîêóñû F
1
è F
2
, à çà îñü Îó
ïåðïåíäèêóëÿð â ñåðåäèíå îòðåçêà F
1
F
2
(ðèñ. 10). Òîãäà óðàâíåíèå
ãèïåðáîëû ïðèìåò âèä:
,1
2
2
2
2
=−
b
y
a
x
(1.39)
ãäå b
2
= ñ
2
à
2
.
Ãèïåðáîëà èìååò äâå îñè ñèììåòðèè (êîîðäèíàòíûå îñè), ñ
îäíîé èç êîòîðûõ (îñüþ àáñöèññ) îíà ïåðåñåêàåòñÿ â äâóõ òî÷êàõ
À
1
è À
2
, íàçûâàåìûõ âåðøèíàìè ãèïåðáîëû. Îòðåçîê À
1
À
2
íàçû-
âàåòñÿ äåéñòâèòåëüíîé îñüþ ãèïåðáîëû, à îòðåçîê B
1
B
2
ìíè-
ìîé îñüþ ãèïåðáîëû.
Òàêèì îáðàçîì, ïàðàìåòðû a è b, âõîäÿùèå â óðàâíåíèå ãè-
ïåðáîëû, ðàâíû åå ïîëóîñÿì.
Ýêñöåíòðèñèòåòîì ãèïåðáîëû íàçûâàåòñÿ îòíîøåíèå ðàññòî-
ÿíèÿ ìåæäó ôîêóñàìè ê åå äåéñòâèòåëüíîé îñè:
.
a
c
e =
(1.40)
Î÷åâèäíî, ÷òî e > 1.
Ðèñ. 10
0
x
y
a
•
•
b
c
A
1
A
2
B
1
B
2
F
1
F
2

46
Ãèïåðáîëà èìååò äâå àñèìïòîòû, óðàâíåíèÿ êîòîðûõ
x
a
b
y =
è (1.41)
x
a
b
y −=
Åñëè ìíèìàÿ îñü ãèïåðáîëû íàïðàâëåíà ïî îñè Îõ è èìååò
äëèíó 2à, à äåéñòâèòåëüíàÿ îñü äëèíîé 2b íàïðàâëåíà ïî îñè Îó,
òî óðàâíåíèå ãèïåðáîëû (ðèñ. 11) èìååò âèä:
.1
2
2
2
2
=+−
b
y
a
x
(1.42)
Ýêñöåíòðèñèòåò òàêîé ãèïåðáîëû âû÷èñëÿåòñÿ ïî ôîðìóëå
.
b
c
e =
Åå àñèìïòîòû òå æå, ÷òî è ó ãèïåðáîëû (1.39).
Ãèïåðáîëû (1.39) è (1.42) íàçûâàþòñÿ ñîïðÿæåííûìè.
Ãèïåðáîëà íàçûâàåòñÿ ðàâíîñòîðîííåé, åñëè åå äåéñòâèòåëü-
íûå è ìíèìûå îñè ðàâíû, ò.å. à = b. Ïðîñòåéøåå óðàâíåíèå ðàâíî-
ñòîðîííåé ãèïåðáîëû èìååò âèä:
x
2
y
2
= à
2
(1.43)
èëè
x
2
+ y
2
= à
2
.
Ðèñ. 11
0
a
•
•
b
c
A
1
A
2
B
1
B
2
F
1
F
2
x
y

47
Ïàðàáîëîé íàçûâàåòñÿ ãåîìåòðè÷åñêîå ìåñòî òî÷åê, ðàâíîóäà-
ëåííûõ îò äàííîé òî÷êè, íàçûâàåìîé ôîêóñîì, è äàííîé ïðÿìîé,
íàçûâàåìîé äèðåêòðèñîé ïàðàáîëû.
Âåëè÷èíà ð, ðàâíàÿ ðàññòîÿíèþ îò ôîêóñà äî äèðåêòðèñû, íà-
çûâàåòñÿ ïàðàìåòðîì ïàðàáîëû; ïðÿìàÿ, ïðîõîäÿùàÿ ÷åðåç ôîêóñ
ïàðàáîëû ïåðïåíäèêóëÿðíî åå äèðåêòðèñå, íàçûâàåòñÿ îñüþ,
à òî÷êà ïåðåñå÷åíèÿ ïàðàáîëû ñ åå îñüþ âåðøèíîé ïàðàáîëû.
Ïðîñòåéøåå óðàâíåíèå ïàðàáîëû ïîëó÷àåòñÿ, åñëè êîîðäèíàò-
íàÿ ñèñòåìà ðàñïîëîæåíà ñëåäóþùèì îáðàçîì: çà îäíó èç êîîðäè-
íàòíûõ îñåé áåðåòñÿ îñü ïàðàáîëû, à çà äðóãóþ ïðÿìàÿ, ïåð-
ïåíäèêóëÿðíàÿ îñè ïàðàáîëû è ïðîâåäåííàÿ ïîñðåäèíå ìåæäó
ôîêóñîì è äèðåêòðèñîé.
Òîãäà óðàâíåíèå ïàðàáîëû ïðèìåò âèä:
y
2
=2px (ðèñ. 12); (1.44)
y
2
=2px (ðèñ. 13); (1.45)
x
2
=2pó (ðèñ. 14); (1.46)
x
2
=2pó (ðèñ. 15). (1.47)
Ðèñ. 14
Ðèñ. 15
Ðèñ. 13Ðèñ. 12
0
x
y
•
2
p
x −=
0;
2
p
F
0
x
y
•
2
p
x −=
0;
2
p
F
0
•
2
p
y −=
2
;0
p
F
x
y
0
•
2
p
y =
2
;0
p
F
x
y

48
Óðàâíåíèå
y = ax
2
+ bx + c (a ≠ 0) (1.48)
îïðåäåëÿåò ïàðàáîëó, îñü êîòîðîé ïåðïåíäèêóëÿðíà îñè
àáñöèññ.
Àíàëîãè÷íî, óðàâíåíèå
x = my
2
+ ny + p (m ≠ 0) (1.49)
îïðåäåëÿåò ïàðàáîëó, îñü êîòîðîé ïåðïåíäèêóëÿðíà îñè
îðäèíàò.
Óðàâíåíèÿ (1.48) è (1.49) ïðèâîäÿòñÿ ê ïðîñòåéøåìó âèäó (1.44
1.47) ïóòåì òîæäåñòâåííûõ ïðåîáðàçîâàíèé ñ ïîñëåäóþùèì ïà-
ðàëëåëüíûì ïåðåíîñîì êîîðäèíàòíîé ñèñòåìû.
Ïðèìåð 1.16. Äàíû âåðøèíû À (2; 1), Â (6; 3), C (4; 5) òðåóãîëü-
íèêà. Íàéòè: 1) äëèíó ñòîðîíû ÀÂ; 2) âíóòðåííèé óãîë À â ðàäèà-
íàõ ñ òî÷íîñòüþ äî 0,01; 3) óðàâíåíèå âûñîòû, ïðîâåäåííîé ÷åðåç
âåðøèíó Ñ; 4) óðàâíåíèå ìåäèàíû, ïðîâåäåííîé ÷åðåç âåðøèíó Ñ;
5) òî÷êó ïåðåñå÷åíèÿ âûñîò òðåóãîëüíèêà; 6) äëèíó âûñîòû, îïó-
ùåííîé èç âåðøèíû Ñ; 7) ñèñòåìó ëèíåéíûõ íåðàâåíñòâ, îïðåäå-
ëÿþùóþ âíóòðåííþþ îáëàñòü òðåóãîëüíèêà. Ñäåëàòü ÷åðòåæ.
Ðåøåíèå.
Äåëàåì ÷åðòåæ (ðèñ. 16).
Ðèñ. 16
x
y
0
D
M
K
B(6; 3)
C(4; 5)
A(2; 1)
<

49
1. Äëèíó ñòîðîíû ÀÂ íàõîäèì êàê ðàññòîÿíèå ìåæäó äâóìÿ
òî÷êàìè À è Â.
.5220416)13()26(
)()(
22
22
==+=−+−=
=−+−=
ABAB
y
y
xxAB
2. Äëÿ îïðåäåëåíèÿ âíóòðåííåãî óãëà À íàéäåì óðàâíåíèå ïðÿ-
ìîé ÀÑ:
,
2
2
4
1
;
24
2
15
1
;
−
=
−
−
−
=
−
−
−
−
=
−
−
xyxy
xx
xx
yy
yy
AC
A
AC
A
îòñþäà 2õ ó 3 = 0 èëè ó = 2õ 3 è óãëîâîé êîýôôèöèåíò ïðÿìîé
ÀÑ ðàâåí: k
AC
= 2; äàëåå íàõîäèì óðàâíåíèå ïðÿìîé ÀÂ:
,
4
2
2
1
;
26
2
13
1
;
−
=
−
−
−
=
−
−
−
−
=
−
−
xyxy
xx
xx
yy
yy
AB
A
AB
A
îòñþäà
õ 2ó = 0 èëè
xy
2
1
=
è
.
2
1
=
AB
k
Íàõîäèì óãîë À
,75,0
4
3
2
1
21
2
1
2
1
tg ==
⋅+
−
=
⋅+
−
=
ABAC
ABAC
kk
kk
A
îòñþäà
∠À = 36°52′11″ = 0,64 ðàäèàí.
3. Óðàâíåíèå âûñîòû, ïðîâåäåííîé ÷åðåç âåðøèíó Ñ, èùåì
â âèäå y y
C
= k
CD
(x x
C
) è òàê êàê ÑD ⊥ ïðÿìîé ÀÂ, òî
.2
5,0
11
−=−=−=
AB
CD
k
k
Òîãäà
ó 5 = 2(õ 4), èëè 2õ + ó 13 = 0, èëè ó = 2õ + 13.

50
4. Äëÿ îïðåäåëåíèÿ óðàâíåíèÿ ìåäèàíû ÑÌ íàõîäèì êîîðäè-
íàòû òî÷êè Ì, êîòîðàÿ äåëèò ïðÿìóþ À ïîïîëàì
.2
2
31
2
;4
2
62
2
=
+
=
+
==
+
=
+
=
BA
M
BA
M
y
y
y
xx
x
Óðàâíåíèå ïðÿìîé ÑÌ èùåì â âèäå:
,
0
4
3
5
;
44
4
52
5
;
−
=
−
−
−
=
−
−
−
−
=
−
−
xyxy
xx
xx
yy
yy
CM
C
CM
C
à ýòî îçíà÷àåò, ÷òî óðàâíåíèå ìåäèàíû èìååò âèä õ = 4, ò.å. ïðÿ-
ìàÿ ÑÌ ⊥ Îõ.
5. Òî÷êó ïåðåñå÷åíèÿ âûñîò òðåóãîëüíèêà íàéäåì êàê òî÷êó Ê
ïåðåñå÷åíèÿ âûñîò ÑD è ÂÊ.
Íàõîäèì óðàâíåíèå âûñîòû ÂÊ:
y y
B
= k
BK
(x x
B
), èëè
),(
1
B
AC
B
xx
k
y
y
−−=−
èëè
),6(
2
1
3 −−=− xy
èëè x + 2y 12 = 0.
Ðåøàåì ñèñòåìó óðàâíåíèé, îïèñûâàþùèõ ïðÿìûå ÑD è ÂÊ:
.0113
2
.0122
,0132
=+−
⋅
−
=−+
=−+
y
yx
yx
Òîãäà
3
11
=y
è
,
3
14
3
11
212212 =⋅−=−= yx
ò.å. êîîðäèíàòû òî÷-
êè Ê áóäóò:
.
3
11
,
3
14
K
6. Äëÿ íàõîæäåíèÿ äëèíû âûñîòû ÑD çàïèøåì íîðìàëüíîå
óðàâíåíèå ïðÿìîé ÀÂ:
,0
)2()1(
2
22
=
−+±
− yx
èëè
.0
5
2
=
±
− yx
