Sha W., Malinov S. Titanium Alloys: Modelling of Microstructure, Properties and Applications

Подождите немного. Документ загружается.

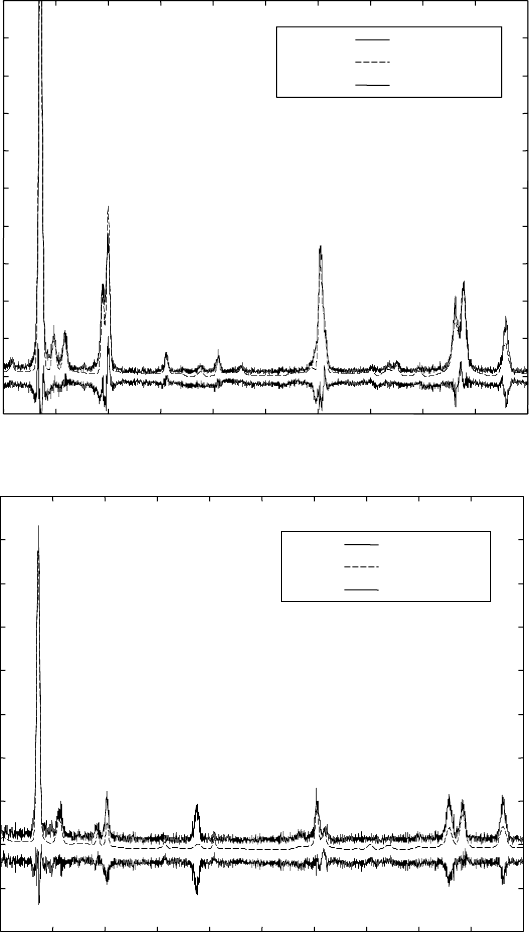
Synchrotron radiation X-ray diffraction 55

upper observed

calculated

lower difference

Forged

35 40 45 50 55 60 65 70 75 80 85

2θ (°)

(a)

{020}α

{011}B2

{021}α

{022}α

{002}B2

{023}α

{112}B2

Intensity (c.p.s.)

1000

900

800

700

600

500

400

300

200

100

3.13

X-ray diffraction patterns, calculated profiles (dotted lines) and

the difference curves for (a) forged and (b) and (c) heat treated Ti-

46Al-1.9Cr-3Nb alloy with different cooling rates from 1450 °C. The

reflections of the B2 and the α

phases are indexed. All the other

reflections belong to the γ phase.

upper observed

calculated

lower difference

5 °C/min

35 40 45 50 55 60 65 70 75 80 85

2θ (°)

(b)

{021}α

{022}α

{222}α

Intensity (c.p.s.)

400

350

300

250

200

150

100



Titanium alloys: modelling of microstructure56

diffraction pattern instead of using single reflections. The principle of averaging

the integral intensities is applied.

All the diffraction patterns from the alloy with different cooling rates

confirm that the alloy is in the two-phase state: γ phase (about 97 wt.%) and

phase (about 3 wt.%), in agreement with previous literature (Guo et al.,

2001; Hao et al., 2000). The amount of α

phase varies from 1.5 wt.% to

5 wt.% under different cooling rates. The highest content of α

phase

corresponds to the fastest cooling rate (50 °C/min) and the lowest corresponds

to the slowest rate (5 °C/min), the same as was reported by Qin et al. (2000).

This proves that the α to γ transformation with lamellar formation is quite

sluggish, which makes the subsequent ordering of the remaining α phase,

α + γ to α

+ γ, more favourable at high cooling rates. At very high cooling

rates such as those during water quenching, the mechanism of the transformation

is different and the α to γ transformation takes place in a massive fashion, in

which case there is no retained α

phase.

The low volume fraction of the α

phase has also been found by Qin et al.

(2000) and Guo et al. (2001). With the addition of chromium, the fraction of

the α

decreases, and the addition of niobium to the Ti-46Al binary alloy

does not change much the volume fraction of the α

phase (Hao et al., 2000).

The different intensities of the peaks attributed to the α

phase are explained

upper observed

calculated

lower difference

50 °C/min

35 40 45 50 55 60 65 70 75 80 85

2θ (°)

(c)

{021}α

{022}α

Intensity (c.p.s.)

500

450

400

350

300

250

200

150

100

{023}α

3.13

Continued



Synchrotron radiation X-ray diffraction 57

by the presence of the different types of preferred orientations in the different

samples. The Rietvield–Toraya model is used in the calculation to take into

account the preferred orientation effect.

The alloy in the forged state differs significantly from the others. Its

diffraction pattern shows vividly the presence of the third phase, namely the

bcc ordered B2 phase, due to the presence of chromium alloying element in

the composition. The content of B2 phase is just about 1 wt.%, but it manifests

itself by the presence of the strongest {011} reflection. There is no evidence

of the B2 phase in heat-treated samples, for above 1200 °C the B2 phase

disappears by solid solution in the α

+ γ matrix. The lattice parameter of the

B2 phase is 0.3186 nm.

The results of matching of the calculated to experimental intensity profiles

are satisfactory. For the forged alloy, for example, such indicators of progress

of a refinement as R-factors are R

= 16.8% with R

expected

= 13.43%. The

pattern R-factor is defined as

oi ci

| – |

| |

, where y

is the observed

intensity at the ith step, y

is the calculated intensity at the ith step, and the

sum is over all data points. R

expected

characterises the observed pattern and

includes the total number of data points, the number of parameters adjusted

and the number of constraints applied.

The lattice parameters of the structure of γ phase matched are presented

in Table 3.2. The heat treatment affected the lattice parameter a and the

tetragonality degree. The tetragonality of the γ phase unit cell is smaller in

the forged state than in the state after heat treatment.

The difference in the lattice parameters of the forged and heat-treated

states might reflect the difference between the chemical compositions of

these states. Addition of chromium decreases tetragonality, compared with

other alloying elements. In the forged state c/a is much smaller than that in

typical manganese-containing alloys.

Table 3.2

Values of the lattice parameter

and tetragonality

for γ phase

in forged Ti-46Al-1.9Cr-3Nb alloy and the alloy after heat treatment with

different cooling rates

Heat treatment Lattice parameter

(nm) Tetragonality

Forged 0.4013 1.011

5 °C/min 0.3997 1.019

10 °C/min 0.3982 1.022

20 °C/min 0.3999 1.018

30 °C/min 0.3999 1.017

40 °C/min 0.3998 1.016

50 °C/min 0.4002 1.016



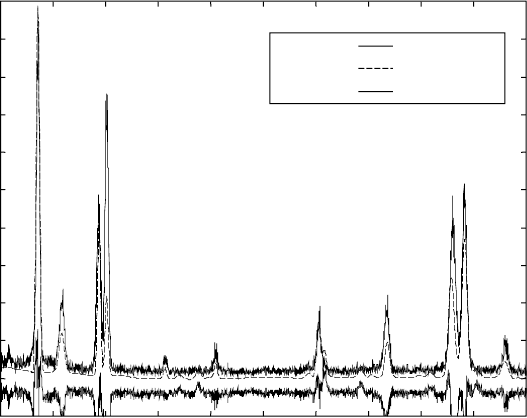
Titanium alloys: modelling of microstructure58

3.4.2 High-temperature study of phases

In situ studies of the phase changing are not common for TiAl-based

alloys.

This section applies synchrotron radiation high-resolution XRD

measurements to show in situ the composition of the phases in the Ti-46Al-

1.9Cr-3Nb alloy over a wide temperature range, up to 1450 °C, with the

objective of understanding the processes at the alloy surface during high-

temperature exposure.

Diffraction

Alloy phases

The quantitative phase analysis identifies the exact set of phases in the alloy

and deduces the amount of each phase at each temperature. An example of

the results after using the fitting procedure for an experimental X-ray diffraction

pattern is shown in Fig. 3.14.

1200 °C

{104}Al

{002}α

Intensity (c.p.s.)

10000

9000

8000

7000

6000

5000

4000

3000

2000

1000

observed

upper calculated

lower difference

{100}Ti

{002}Ti

{011}B

{101}Ti

{021}α

{012}α

+ {113}Al

{002}γ

{020} γ

29 30 31 32 33 34 35 36 37 38

2θ (°)

{111}γ

3.14

X-ray diffraction pattern, calculated profile and the difference

curve for the Ti-46Al-1.9Cr-3Nb alloy at 1200 °C. All the reflections

are indexed.



Synchrotron radiation X-ray diffraction 59

The results of matching the calculated-to-experimental intensity profiles

are acceptable. For the pattern in Fig. 3.14, for example, R

= 8.47% with

expected

= 4.93%.

The alloy under study transforms in the following sequence upon slow

cooling from the liquid: L → β + L → β → β + α → α → α + γ → α

+ γ

+ B2. The diffraction patterns in the range of 20–1450 °C indicate that the

alloy is in the two-phase (γ and α/α

phases) state mostly and has the ordered

bcc B2 phase – the third phase – at some temperatures.

Niobium substitutes mainly titanium sites, while chromium substitutes

either titanium or aluminium sites depending upon the aluminium content

(Ducher et al., 2002), but, in our models below, we use only titanium and

aluminium atoms, assuming the equatomic composition.

The structure of α-Ti is disordered A3, which belongs to the space group

. We used the setting P6

/mmc with:

A : 2(c) :

, B : 2(c) :

. [3.2]

The values of the lattice parameters at 1300 °C, as a result of fitting, are a =

0.58128 nm; c = 0.46667 nm.

The structure of Ti

Al α

phase is ordered DO

, which belongs to the

space group

. We used the setting P6

/mmc with:

A : 2(c) :

, B : 6(h) : , 2 ,

. [3.3]

The values of the lattice parameters at room temperature and atomic coordinates,

as a result of fitting, are a = 0.5764 nm; c = 0.4664 nm; x = 0.8333.

The structure of TiAl γ phase is ordered L1

, which belongs to the space

group

. We used the setting P4/mmm with:

A : 1(a) : 1. 0, 0, 0, 1(c) : 2.

,0,

B : 2(e) : 1. 0,

, 2.

, 0,

[3.4]

The values of the lattice parameters at room temperature, as a result of

fitting, are a = 0.40126 nm; c = 0.40591 nm.

The transformation of the phases above, disordering of the ordered γ and

phases with temperature, results in appearance of α-Ti phase reflections

above 1200 °C. This, its further growth and the decreasing of the integral

intensities of the γ phase reflections as the temperature increases are clearly

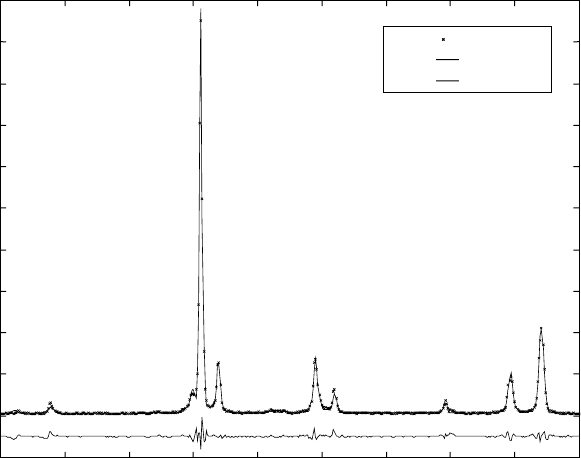
seen in Fig. 3.15, which shows the evolution of the phases. The reflections

of all the phases become sharp with temperature, to δ-like theoretically, due

to phase homogenization and grain growth.

The temperature dependency of the lattice parameters for the γ and α/α

phases is presented in Fig. 3.16. The coefficients of thermal expansion (CTE)



Titanium alloys: modelling of microstructure60

in the temperature range of 20–1450 °C can be derived by comparing the

lattice parameters at high- and room-temperatures, although the CTE are

known to be influenced by the quantity of thermal vacancies, not only by

change in lattice parameters. A comparison of the derived values for both γ

and α/α

phases and some previously published data are shown in Table 3.3.

There is a big difference between the CTE along the a and c axes of the γ

phase, but there is only a quite slight difference between the CTE along the

a and c axes of the α/α

phase. Such different behaviour for γ and α/α

phases is because adjacent γ and α/α

phases have the crystallographic

relationship

[110] / /[1120]

γα

and {111}γ//{0001}α

The published data refer to different alloy compositions, and more

importantly, were obtained from a different technique of CTE measurement

(Zhang et al., 2001; Zupan and Hemker, 2001). The technique used by

Zhang et al. (2001) and Zupan and Hemker (2001) is single crystal capacitance

dilatometry, which is unable to distinguish the two phases, if present. Only

the bulk linear expansion is measured (Zhang et al., 2001; Zupan and Hemker,

Intensity (c.p.s.)

10000

8000

6000

4000

2000

30 31 32 33 34 35 36 37 38

2θ (°)

{111} γ

{002} α

{021} α

{002} γ

{020} γ

1450 °C

1400 °C

1300 °C

1200 °C

1100 °C

1000 °C

900 °C

800 °C

400 °C

3.15

X-ray diffraction patterns for Ti-46Al-1.9Cr-3Nb, showing the

evolution of the transformation with temperature. The reflections of

the γ and the α phases are indexed. All the other reflections belong

to the titanium and aluminium oxides.



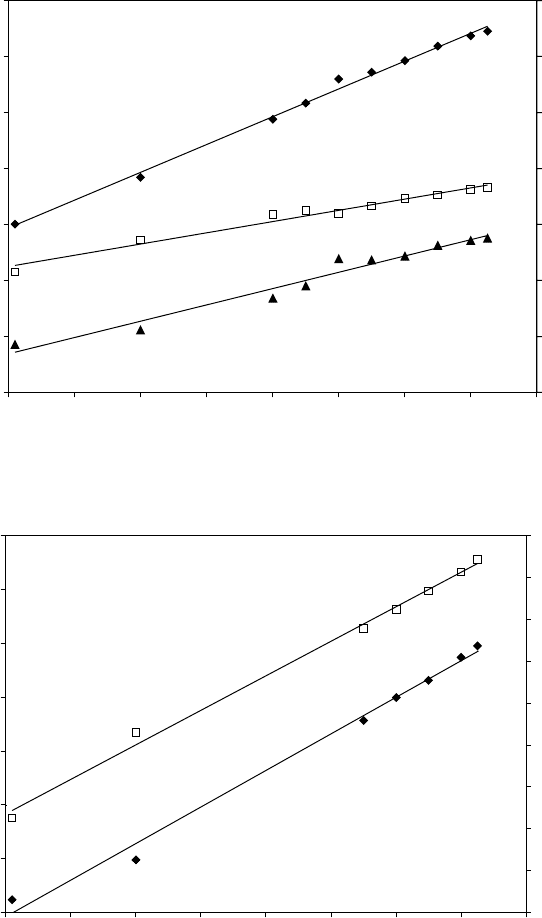
Synchrotron radiation X-ray diffraction 61

0 200 400 600 800 1000 1200 1400 1600

(°C)

(a)

c/a

Lattice parameters (nm)

0.412

0.41

0.408

0.406

0.404

0.402

0.4

0.398

Tetragonality degree

c/a

1.035

1.03

1.025

1.02

1.015

1.01

1.005

0 200 400 600 800 1000 1200 1400 1600

(°C)

(b)

Lattice parameter

(nm)

0.581

0.58

0.579

0.578

0.577

0.576

0.575

0.574

Lattice parameter

(nm)

0.4675

0.467

0.4665

0.466

0.4655

0.465

0.4645

0.464

0.4635

0.463

3.16

(a) Lattice parameters and tetragonality degree for γ phase, and

(b) lattice parameters for α/α

phase as functions of temperature of

Ti-46Al-1.9Cr-3Nb alloy.



Titanium alloys: modelling of microstructure62

2001). For multiphase alloys, the CTE is a complicated function of the

thermal and elastic properties of the individual components, as well as the

electronic structure, so the difference between our data and the published

ones (Table 3.3) is the result of the different composition of the alloys under

comparison. The lower thermal expansion, as in the case of the alloy used

here, offers a potential advantage in lower thermal stresses and increasing

thermal shock and fatigue resistance. The CTE for this alloy is obtained

independently for both γ and α/α

phases in both [100] and [001] directions.

The temperature dependency of atomic volume for both γ and α/α

phases

is given in Fig. 3.17. The relative change in the volume per atom for γ phase

during ordering, i.e. between 1100 and 1300 °C, is 0.4%, and for α/α

phase

0.3%. The volume change of the same order is typical for the martensitic

transformation of austenite, or B2 to R type in NiTi (Daróczi et al., 2000).

The diffraction patterns in the range of 800–1100 °C show the presence of

B2 phase. The content of B2 phase is about 1 wt.%. Figure 3.18 illustrates

the evolution of the phase with temperature. Above 1200 °C, the B2 phase

disappears by solid solution in the more close-packed α + γ matrix. B2 phase

is a grain growth restricting agent, and thus, as soon as the B2 phase disappears,

large α phase colonies having uniform orientation of the lamellae upon

cooling form, resulting in a remarkable increase of the scale of microstructure.

An ordered B2 structure belongs to the space group

. We used the

setting Pm3m with:

A : 1(a) : 0, 0, 0,

B : 1(a) :

. [3.5]

The value of the lattice parameter at elevated temperatures is 0.31893 nm,

which correlates well with Zhang et al. (2000).

Table 3.3

Thermal coefficients of linear expansion of γ-TiAl alloys

Alloy Phase Temperature Reference Coefficient of thermal

composition interval (°C) expansion, ×10

–6

/°C

direction

Ti-46Al- γ 20–450 – 5.1 12.4

1.9Cr-3Nb

Ti-55.5Al γ 400–1000 Zupan and 14.0 13.0

Hemker (2001)

Ti-46Al- α/α

20–1450 – 5.7 4.8

1.9Cr-3Nb

Ti-47Al- Mean 20–1000 Zhang

et al.

9.7 9.7

4(Nb,W,B) (2001)



Synchrotron radiation X-ray diffraction 63

Oxide phases

At high temperatures, starting from 1100 °C, the reflections of Ti

O phase

are present in the diffraction patterns, and of Al

starting from 1200 °C.

The vacuum level (15 mPa) of the furnace chamber was not sufficient to

completely prevent oxidation. The titanium aluminides are characterized by

a strong tendency to form TiO

(Tang et al., 2002) and protective Al

scales at 1200 °C (Palm et al., 2002; Tang et al., 2002). Some authors report

the presence of TiO oxide in γ-TiAl-based alloys (Li X Y et al., 2003; Li Z

et al., 2003).

The structure of α-Al

belongs to the space group

. We used the

setting

R3cH

with:

A : 12(c) : 0, 0, z, B : 18(e) :

x,0,

. [3.6]

The values of the lattice parameters at elevated temperatures and atomic

coordinates, as a result of fitting, are a = 0.47949 nm; c = 1.30995 nm; x =

0.8333; z = 0.35274.

Both TiO and TiO

models are inadequate when applied to the diffraction

patterns. The only structure that shows good R-factors during fitting procedure

is the structure of Ti

O oxide.

0 200 400 600 800 1000 1200 1400 1600

(°C)

Volume per atom of γ phase (10

–2

)

6.8

6.75

6.7

6.65

6.6

6.55

6.5

6.45

6.4

Volume per atom of α phase (10

–2

)

13.9

13.8

13.7

13.6

13.5

13.4

13.3

13.2

3.17

Volume per atom for γ and α/α

phases as a function of

temperature of Ti-46Al-1.9Cr-3Nb alloy.



Titanium alloys: modelling of microstructure64

The structure of Ti

O belongs to the space group

. We used the setting

P31m

with:

A : 1(a) : 0, 0, 0,

B : 2(d) :

, .z

[3.7]

The values of the lattice parameters at elevated temperatures and atomic

coordinates, as a result of fitting, are a = 0.29194 nm; c = 0.47130 nm; z =

0.13937.

Phase equilibria

The phase equilibria for the composition of the alloy at different temperatures

calculated with the Thermo-Calc software and using a TiAl-database are

presented in Fig. 3.19a. From the experimental data, the molar fraction for

each phase can be derived using the full-profile quantitative phase analysis

(Fig. 3.19b). This phase diagram is not complete, for the content of B2 is

about 1 mol% (also 1 wt.%), and the experiments are conducted only up to

33 33.1 33.2 33.3 33.4 33.5

2θ (°)

Intensity (c.p.s.)

1100

1000

900

800

700

600

500

400

300

200

100

{011} reflection of B2 phase

1200 °C

1100 °C

1000 °C

900 °C

800 °C

400 °C

3.18

X-ray diffraction patterns, showing the evolution of {011}

reflection of B2 phase with temperature for Ti-46Al-1.9Cr-3Nb alloy.

For clarity, the diffraction patterns are shifted with respect to each

other along the vertical axis.

