Sha W., Malinov S. Titanium Alloys: Modelling of Microstructure, Properties and Applications

Подождите немного. Документ загружается.

Titanium alloys: modelling of microstructure118

under isothermal conditions. An in-situ electrical resistivity technique is

introduced to experimentally study the course of the transformation.

Experimental procedures are described in original research papers (Malinov

et al., 2001, 2002, 2003; Markovsky et al., 2004). The kinetics are traced

within the theoretical frame of the JMA theory.

6.2 Resistivity experiments

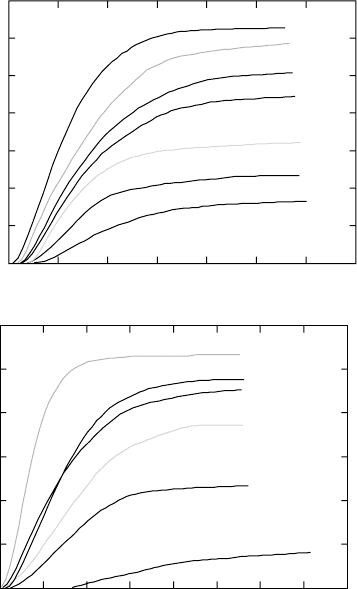
Following experiments, sets of curves showing the relative increase of the

resistivity during isothermal exposure (∆R/R

) versus time for different

temperatures can be recorded. Typical resistivity curves are shown in Fig.

6.1. Generally, for all these alloys, there is increase of resistometric signal

∆

R/R

(%)

3.5

2.5

1.5

0.5

(a) Ti-6Al-4V

0 10203040506070

Time (sec)

750 °C

800 °C

850 °C

870 °C

900 °C

920 °C

950 °C

∆

R/R

(%)

(b) Ti-6Al-2Sn-4Zr-2Mo-0.08Si

0 10203040 50607080

Time (sec)

735 °C

750 °C

800 °C

850 °C

900 °C

930 °C

6.1

Resistivity data at different temperatures of isothermal exposure

(a) Ti-6Al-4V; (b) Ti-6Al-2Sn-4Zr-2Mo-0.08Si; (c) Ti-8Al-1Mo-1V;

(d) β21s. For clarity, the resistivity curves are shifted with respect to

each other along the vertical axis.



The Johnson–Mehl–Avrami method 119

with lowering of temperature. Two factors may have influence on the resistivity:

(i) different amounts of the α and the β fractions, e.g. the increase of the α

fraction, and (ii) change of the compositions of the α and the β phases, e.g.

the enrichment of the β phase with vanadium in the case of Ti-6Al-4V. In

order to separate the above two effects, calibration curves are needed. The

results from the optical microscopy quantitative study of samples quenched

after heating to different temperatures for different times can be used to

build the calibration curves of the relative resistance (∆R/R

) versus the

∆

R/R

(%)

0 10 203040 5060 70

Time (sec)

750 °C

800 °C

850 °C

900 °C

925 °C

950 °C

975 °C

∆

R/R

(%)

2.5

1.5

0.5

(d) β21s

0 20 40 60 80 100 120

Time (min)

750 °C

700 °C

650 °C

600 °C

500 °C

400 °C

6.1

Continued



Titanium alloys: modelling of microstructure120

amount of precipitated α phase (%) for each alloy. Such calibration curves

are necessary for converting resistivity data into α phase fraction. For Ti-

6Al-4V, Ti-6Al-2Sn-4Zr-2Mo-0.08Si, and Ti-8Al-1Mo-1V alloys, linear

relations between ∆R/R

and the amount of α are found. The linear relation

is well proved and very clear when the degree of transformation varies

between about 10 and 90%. The relative error of the calibration curve within

this range is about 5%. For the very early stages (<10% degree of

transformation) as well as for the final stages (>90% degree of transformation),

there are some deviations from the linear relation and larger errors are possible.

The following remarks on the resistivity effect are also significant:

• Only primary α phase has influence on the resistivity effect, because just

this phase is formed during the isothermal exposure. Secondary α phases,

i.e. α′ or α″ martensite, are formed as a result of residual β phase

decomposition on subsequent quenching or further cooling, which allows

one to evidently recognise and numerically evaluate the quantity of

phases formed at different stages of β decomposition. Their influence on

resistivity is not considered when studying the β phase decomposition

under isothermal conditions only.

• The effects of α, α′ and α″ phases on the resistivity differ mainly in the

kinetics and the temperature ranges when these transformations take

place on cooling. In the present case, resistivity is used for studying

stable α phase formation under isothermal conditions.

• The different morphology of the α phase in the initial state, before

heating to the single β-phase field, can influence the initial value of the

specimen resistivity (R

). However, there is no difference in the material’s

behaviour after solid solutioning at temperatures above β-transus, because

alloys with any starting microstructure become the same, consisting of

coarse grains of β phase.

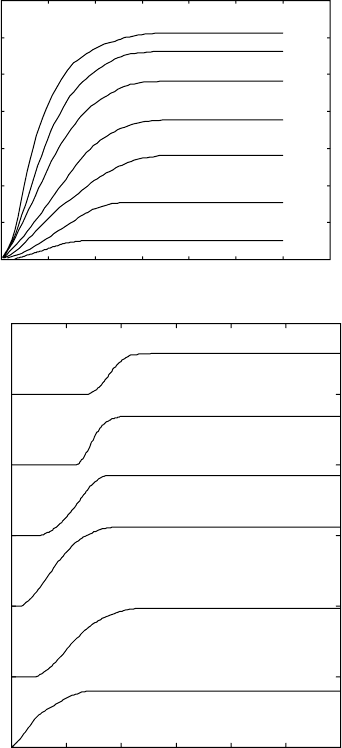
Using the aforementioned calibration relations, the experimental resistivity

curves can be recalculated or converted to give the amounts of α phase

versus time, for different holding temperatures (Fig. 6.2a–c), which trace the

kinetics of the β to α + β transformation for the Ti 6-4, the Ti 6-2-4-2 and the

Ti 8-1-1 alloys. These data can be further used for modelling and simulations.

At different temperatures of isothermal exposure, different final amounts of

the α phase are obtained. For titanium alloys, the transformation of β to α +

β is of monovariant type. At different temperatures, different amounts of α

and β phases are in equilibrium. There are different equilibrium compositions

of both phases at different temperatures. This observation will be discussed

in more detail in Section 6.6.

The composition of the alloy β21s corresponds to an aluminium equivalent,

[Al]

, of 3 wt.%, and molybdenum equivalent, [Mo]

, of 15.8 wt.%. This

composition determines the alloy as a metastable β titanium alloy (Boyer



The Johnson–Mehl–Avrami method 121

(a) Ti-6Al-4V

750 °C

800 °C

850 °C

870 °C

900 °C

920 °C

950 °C

010203040506070

Time (sec)

Amount of α phase (vol. %)

100

(b) Ti-6Al-2Sn-4Zr-2Mo-0.08Si

735 °C

750 °C

800 °C

850 °C

900 °C

930 °C

010 20304050607080

Time (sec)

Amount of α phase (vol. %)

100

6.2

Kinetics of the β to α + β transformation at different temperatures

of isothermal exposure (a) Ti-6Al-4V; (b) Ti-6Al-2Sn-4Zr-2Mo-0.08Si;



Titanium alloys: modelling of microstructure122

et al., 1994). Hence, initial homogeneous β structure tends to precipitate α

phase upon isothermal exposure at temperatures in the α + β equilibrium

range. The alloy has α + β phase composition in the condition normally

supplied for commercial use. Before resistivity measurement, the samples

should be heated up to the β homogenisation field, e.g. 1000 °C, and held for

30 minutes. In order to check the completeness of the β homogenisation, one

can cool samples from this stage to room temperature. The results from

synchrotron X-ray study have shown that the phase composition in both air

750 °C

800 °C

850 °C

900 °C

925 °C

950 °C

975 °C

0 10203040506070

Time (sec)

Amount of α phase (vol. %)

100

(d) β21s

0 102030405060

Time (min)

Amount of α phase (vol. %)

650 °C

600 °C

700 °C

500 °C

750 °C

6.2

Continued



The Johnson–Mehl–Avrami method 123

cooled and water quenched samples is homogeneous β phase, confirming

that at this stage the initial α + β structure has transformed to β. After the β

homogenisation, samples can be cooled rapidly to the chosen holding

temperature and then isothermally held at this temperature when the

resistometric signal is recorded. A set of curves of ∆R/R

versus time for

different temperatures of isothermal exposure can be recorded (Fig. 6.1d).

These curves trace the course of the α phase precipitation from the metastable

β phase at the temperatures studied. Some observations from the recorded

resistivity signals are discussed below.

The resistivity curve at 400 °C is inconsistent with the results for the other

temperatures. The signal shows immediate change of the resistivity from the

very beginning of the isothermal exposure. The difference between the initial

and the final values in ∆R/R

is smaller as compared to the other temperatures.

In addition, the curve shape is different. A possible reason for this difference

is that, at this temperature, the transformation is not purely diffusional β to

α transformation, but some precipitation of metastable phases, such as ω

phase, may be involved. This temperature is not included in the further

analysis.

Decomposition of the metastable β phase in the β21s alloy due to its

higher content of β stabilising elements is considerably slower, including a

pronounced incubation period (Fig. 6.1d). The longest incubation period

(about 28 min) is at 750 °C. This decreases when the temperature is lower.

The minimum value, i.e. the shortest, is for isothermal exposure at 600 °C.

Further decrease of the temperature to 500 °C results in increase of the

incubation time. These results indicate that the ‘nose’ point of the TTT

diagram for this alloy should be around 600 °C. The resistivity curves at all

temperatures tend to become horizontal after one hour isothermal exposure.

This means that the transformation is either completed or the rate of the

transformation is very slow and practically undetectable with the resistivity

method used.

In order to recalculate and transform the resistivity curves to curves showing

the amount of α phase versus time, we need to create calibration curves

between the resistivity signal and the amount of the α phase. Samples quenched

from different temperatures and after different times are studied by light

microscopy (Fig. 6.3). Large deviations in the estimated amounts of the α

phase are detected and the results from the metallography study are found to

be too statistically unreliable to be used for the calibration purpose. The

reason for this is the small amount and the fine microstructure of the α phase.

6.3 Metallography

The typical microstructures of Ti-6Al-2Sn-4Zr-2Mo-0.08Si and Ti-6Al-4V,

and Ti-8Al-1Mo-1V alloys after isothermal exposure at different temperatures



Titanium alloys: modelling of microstructure124

and subsequent quenching are presented in Figs. 6.4 and 6.5, respectively,

illustrating distinct difference in morphology observed between primary

and secondary α phases. First, it is necessary to point out that the α phase

covering the β grain boundary is observed in all cases of isothermal exposure

for both Ti-6Al-2Sn-4Zr-2Mo-0.08Si and Ti-6Al-4V alloys. This may be

explained by the comparatively low (300 °C/s) cooling rate after β solution

treatment. For the Ti 6-4 alloy, the critical cooling rate that depresses

completely all diffusion processes of alloying element redistribution should

be about 400 °C/s or higher. For the more diluted Ti 6-2-4-2 alloy, the critical

cooling rate is even higher (≥500 °C/s). Hence, some diffusion processes

may take place during the cooling at an insufficient rate from the β field to

the temperature of isothermal exposure. These processes cause grain boundary

α formation.

6.3.1 Ti 6-2-4-2 alloy

The as-quenched microstructure after isothermal exposure at 950 °C is

characterised by the presence of a fine grain boundary α phase (Fig. 6.4a).

The total amount of diffusionally grown α phase is about 8%. The remaining

volume fraction is occupied by a martensitic phase, which is formed from

the β phase on subsequent cooling. The matrix, martensite, microstructure is

not homogeneous. This is due to the complex mechanism of the transformation,

including partial diffusional redistribution of β alloying elements and

diffusionless martensitic transformation. (Note that the cooling rate after

20 µm

6.3

Microstructure of β21s alloy after isothermal exposure at 650

°C

(dark field optical image).



The Johnson–Mehl–Avrami method 125

50 µm

(d) (e) (f)

100 µm

50 µm

20 µm

(a) (b) (c)

25 µm

(g)

6.4

Microstructures of (a–c) Ti-6Al-2Sn-4Zr-2Mo-0.08Si and (d–g) Ti-

6Al-4V alloys after different temperatures of isothermal exposure and

subsequent quenching. (a) 950 °C; (b) 900 °C; (c) 850 °C; (d) 920 °C;

(e) 870 °C; (f) and (g) 850 °C.



Titanium alloys: modelling of microstructure126

25 µm

(a)

25 µm

(b)

25 µm

(c)

40 µm

(d)

(e)

25 µm

(f)

25 µm

6.5

Microstructures of Ti-8Al-1Mo-1V alloy after different

temperatures of isothermal exposure and subsequent quenching.

(a) 925 °C; (b) 900 °C; (c) and (d) 850 °C; (e) 800 °C; (f) 750 °C.



The Johnson–Mehl–Avrami method 127

isothermal exposure, 300 °C/s, is not high enough for pure martensitic

transformation).

A decrease of the temperature of isothermal exposure down to 900 °C

causes formation of a coarse α phase covering β grain boundaries. In addition,

some amount of α phase has diffusionally nucleated and grown from the

boundaries (Fig. 6.4b). The amount of the α phase is higher in small β grains

as compared to in big ones. This observation may be associated with the

influence of the grain boundary energy, which is proportional to the grain

boundary curvature. The total amount of diffusionally formed α phase at

900 °C is 38%.

Lower temperatures of isothermal exposure lead to a complete change of

the mechanism of α phase formation. In addition to the grain boundary α

phase, formed on cooling from the β field to the temperature of isothermal

exposure, an α phase nucleated and grown homogeneously inside the former

β grains is observed (Fig. 6.4c). The total amounts of α phase are 69 and

80% for 850 and 800 °C, respectively. The main difference between specimens

exposed at 850 and 800 °C is the different dispersion of the α lamellae –

finer lamellae are attributed to lower temperatures. This may be explained

by the higher contribution from the nucleation process in comparison to the

growth when the temperature of isothermal exposure is lower. Nevertheless,

in both cases, the morphology of the α phase allows one to suppose that it is

formed with partial participation of diffusionless (shifting) processes.

6.3.2 Ti 6-4 alloy

In the specimen exposed at 950 °C and then quenched, a diffusionally formed

α phase is found on some β grain boundaries, as a thin layer covering the

boundaries. The volume fraction of the α phase is about 16%. After exposure

at 920 °C (Fig. 6.4d), the morphology of the α phase, formed as a result of

diffusional decomposition of the β phase, remains the same. Its volume

fraction is slightly increased, to 20%. At 900 °C, a small portion of grain

boundary α phase, as well as α plates diffusionally grown from them, are

observed. The volume fraction of the α phase is about 38%.

At a lower temperature of 870 °C, the microstructure is changed principally.

Some portions of the α phase nucleated and grown within the β grains

appear, in addition to the grain boundary α phase (Fig. 6.4e). The volume

fraction of the diffusional α phase is about 60%. A further decrease of the

temperature down to 850 °C leads to an increase in the amount of

homogeneously nucleated α phase within the former β grains (Fig. 6.4f and

g). Some martensite is found in the regions close to the β grain boundaries.

A decrease of the temperature down to 800 °C and, especially, to 750 °C

causes further increase of the amount of diffusionally formed α phase, to 72

and 82%, respectively.

