Sha W., Malinov S. Titanium Alloys: Modelling of Microstructure, Properties and Applications

Подождите немного. Документ загружается.

Titanium alloys: modelling of microstructure138

relatively low for commercial titanium alloys dictating that the β to α

transformation takes place at lower temperatures (Chapter 14). It should also

be mentioned that the heat treatment conditions of the samples used by

Boyer et al. (1994) were different. In Boyer et al. (1994) the samples were

studied after heating at different temperatures. In this chapter, the alloys

were after β homogenisation and subsequent isothermal holding at different

temperatures. The different heat treatment may also have an influence on the

amount of α phase.

A comparison of the α phase amounts obtained from resistivity studies at

different temperatures for Ti-8Al-1Mo-1V, Ti-6Al-4V and Ti-6Al-2Sn-4Zr-

2Mo-0.08Si alloys is given in Table 6.3. It is obvious that the amounts of the

α phase are higher in Ti-8Al-1Mo-1V alloy as compared to the α phase

amounts at the same temperatures in Ti-6Al-4V and Ti-6Al-2Sn-4Zr-2Mo-

0.08Si alloys, in agreement with the pseudo binary phase diagram of titanium

alloys. In this diagram, the Ti-8Al-1Mo-1V alloy is to the left-side of the Ti-

6Al-4V and the Ti-6Al-2Sn-4Zr-2Mo-0.08Si alloys, implying that the amount

of α phase in the Ti-8Al-1Mo-1V alloy should be higher.

6.6.3 β21s

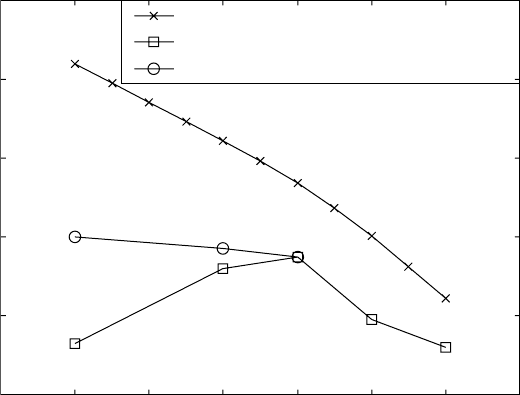
The calculated equilibrium amount of the α phase increases when the

temperature decreases (Fig. 6.10). This tendency is in agreement with the

behaviour of the phase transformation in titanium alloys. However, the large

difference between the calculated and the experimentally observed values,

especially at low temperatures, is apparent. The amounts of the α phase after

resistivity experiments at low temperatures, as discussed earlier in this chapter,

are not the actual equilibrium amounts. Nevertheless, even the amounts of

the α phase after additional ageing, where in the case of 600 °C a phase

equilibrium is believed to be reached, are much lower than the calculated

equilibrium amounts of the α phase. The experimental amounts of the α

phase are believed to be the correct ones and the calculated, especially at low

Table 6.3

Volume fractions of the α phase for Ti-8Al-1Mo-1V, Ti-6Al-2Sn-

4Zr-2Mo and Ti-6Al-4V alloys at various temperatures from resistivity

data

(°C) Ti-8Al-1Mo-1V Ti-6Al-2Sn-4Zr-2Mo Ti-6Al-4V

950 25 – 22

920–930 45 15 32

900 60 43 44

850 77 68 69

800 90 83 79

750 98 87 85



The Johnson–Mehl–Avrami method 139

temperatures are unrealistically high. The calculated amount of the α phase

at 500 °C, for example, is larger than 80% and the tendency is for further

increase of the amount of the α phase as the temperature decreases. Such

high equilibrium amount of α phase in β21s alloy is in contradiction with its

position in the pseudo binary β-isomorphous phase diagram (Boyer et al.,

1994) and the practical knowledge of this alloy. The deviations in the calculated

equilibrium α amount are most probably because this alloy was not used in

the Ti database validation. There is similar discrepancy between calculated

and experimental amounts of the α phase for other titanium alloys (Sections

6.6.1 and 6.6.2).

The major difference in the compositions at different temperatures is the

molybdenum and the niobium contents in the β phase (Fig. 5.7). There is a

tendency for diffusional enrichment of the β phase with both elements when

the temperature decreases. According to the phase diagram, such enrichment

of β phase by β alloying elements is necessary for α phase to be formed.

These calculations show the general characteristics of the phase transformation

in titanium alloys. It is the enrichment with molybdenum and niobium that

stabilises the β phase at room temperature. It should be noted that since the

calculated equilibrium amount of the α phase is deemed too high (Fig. 6.10),

Calculated

Experimental – 2 hours

Experimental – additional ageing

450 500 550 600 650 700 750 800

(°C)

Amount of α phase (%)

100

6.10

Calculated equilibrium amounts of the α phase versus

temperature in the β21s alloy compared with experimentally

observed. The calculations are performed for composition Al = 3.00,

Mo = 14.12, Nb = 3.48, Si = 0.14, Fe = 0.32, C = 0.016, N = 0.024, and

O = 0.15, all in wt.%.



Titanium alloys: modelling of microstructure140

considering the materials balance, the curves tracing the equilibrium

concentrations of alloying elements in the phases (Fig. 5.7b) should also be

shifted. However, the tendency should remain the same. One can conclude

that the β to α + β phase transformation in β21s alloy is connected with

diffusional redistribution of molybdenum and niobium between the α and

the β phases.

6.7 Kinetics of the transformation

In this section, we trace the kinetics of the diffusional β to α + β transformation.

The martensitic (β to α′) transformation is not involved. It was suggested

before on the phase relationship of Ti 8-1-1 that the β phase transforms to

martensite at temperatures in the α + β field from the transus down to about

900 °C. This is not observed in the Ti 8-1-1 alloy as described above. For all

the temperatures ranging from 750 to 975 °C, diffusional β to α transformation

is observed. The martensitic transformation has different kinetics and a distinctly

different resistivity response.

The analysis of the resistivity experimental data can be made within the

framework of the Avrami theory by means of the Johnson–Mehl–Avrami

(JMA) equation. The theory and equation trace the kinetics of the

transformation, giving a relation between the volume fraction of transformed

material and the time. For isothermal transformations, this equation has the

following popular and basic form:

f = 1 – exp(–kt

) [6.1]

where f is the product volume fraction which varies with time t, k is the

reaction rate constant and n is the Avrami index that describes the nucleation

and growth mechanisms.

In its general form, Eq. [6.1] applies to many real transformations. Under

isothermal conditions, it describes a variety of phase transformations including

polymorphic changes, discontinuous precipitation, eutectoid reactions, interface

controlled growth, and diffusion controlled growth. The kinetics of the β to

α + β phase transformation can be modelled by adapting the classic JMA

theory. The above equation can be written in the form:

ykt

()

= = 1– exp(– )

max

[6.2]

where f

(t) is the amount of α phase after a time t,

max

is the maximum

(equilibrium) volume fraction of the α phase at the temperature of the

transformation, and y is the degree of the transformation.

It must be pointed out that the JMA equation describes the transformation

from its start and does not consider the pre-processing stages and the incubation

time. Hence, the time should be treated not as an absolute time but as relative



The Johnson–Mehl–Avrami method 141

to the start of the transformation. This can be taken into account by simple

subtraction of the incubation time.

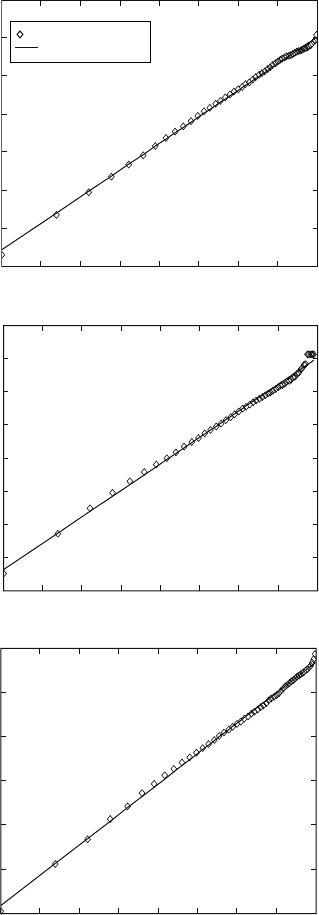
Equation [6.2] can be used to analyse the experimental data by means of

logarithmic plots, where ln(ln(1/(1 – y))) is plotted versus ln(t). The slope of

the linear regression line is the Avrami exponent n, while from the intercept

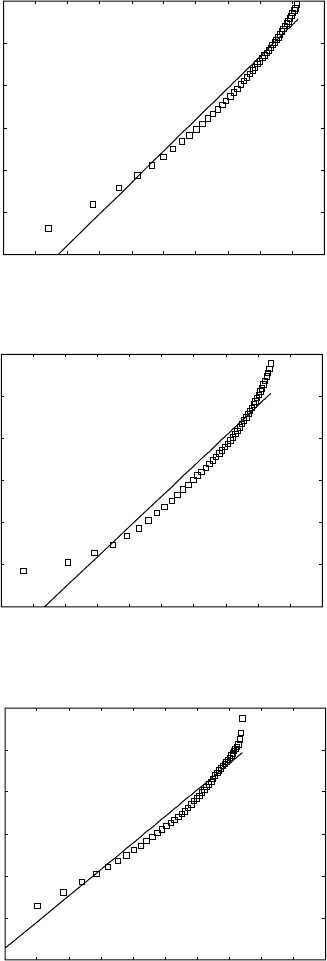
the k value can be calculated. Such plots are presented in Figs. 6.11 and 6.12

for some of the temperatures applied in the resistivity work.

Using the above plots, n and k values for all applied temperatures can be

derived (Tables 6.4 and 6.5).

The Avrami index n obtained from these plots for all temperatures is

within the narrow range of 1.15–1.60 for Ti 6-4 and Ti 6-2-4-2 alloys and

1.26–1.49 for Ti 8-1-1. This corresponds to the mechanism of the β to α +

β transformation in titanium alloys, namely that β-grain boundaries are the

nucleation sites and the α phase has a plate-like morphology.

6.7.1 Ti 6-4 and Ti 6-2-4-2

For all the temperatures, the experimental measurements are described very

well by single straight lines when the plots are in the above coordinate

system. This confirms that the JMA theory can be applied to describe the

kinetics of the β to α + β phase transformation in the titanium alloys under

isothermal conditions. Moreover, the mechanism of the transformation does

not change during the course of the transformation. In near-β titanium alloys

(Ti 10-2-3 and β-CEZ), the mechanism of the transformation changes during

the course of the transformation when the transformation takes place at low

temperatures (350 °C), indicated by obvious changes of the line slope. Such

effects are not observed here.

Note, however, that although the above plots are the most usual means of

deriving the JMA kinetics parameters, such a free approach may be misleading.

The reader will find that acceptable good fittings between the experimental

and the calculated fractions are possible for any n value ranging within 1.2–

1.5 and for all curves in Fig. 6.2a and b. Since n is correlated with the

nucleation and growth mechanisms (the geometry of the transformation), the

next conclusion is that the mechanism of the transformation does not change

in the temperature ranges concerned. This conclusion is valid for most

transformations over appreciable temperature ranges. Thereby, the next step

is to fit the experimental data in Fig. 6.2a and b to the JMA equation, Eq.

[6.2], by setting the n value free but constant for all the temperatures used.

This can be performed by an optimisation computer program, trying to minimise

the sum square error between the experimental and calculated fractions for

all temperatures. From such calculations, the values of n = 1.31 for Ti 6-4

and n = 1.44 for Ti 6-2-4-2 are obtained.

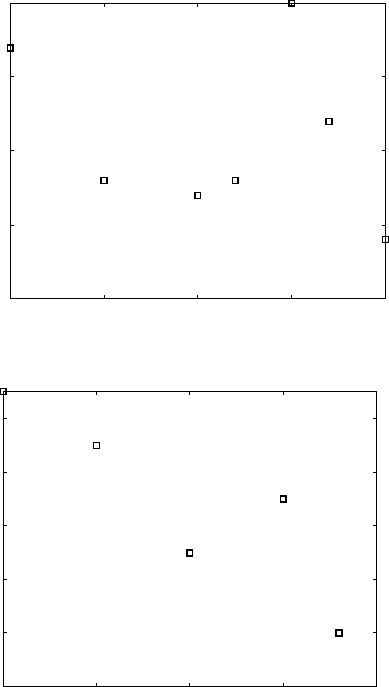
The temperature dependence of the rate constant is not monotonic in the



Titanium alloys: modelling of microstructure142

Data

Best linear fit

In(In(1/(1–

)))

–1

–2

–3

–4

0 0.5 1 1.5 2 2.5 3 3.5 4

In(

)

(a) Ti-6Al-4V (750 °C)

In(In(1/(1–

)))

–1

–2

–3

–4

–5

0 0.5 1 1.5 2 2.5 3 3.5 4

In(

)

(b) Ti-6Al-2Sn-4Zr-2Mo-0.08Si (750 °C)

In(In(1/(1–

)))

–1

–2

–3

–4

0 0.5 1 1.5 2 2.5 3 3.5 4

In(

)

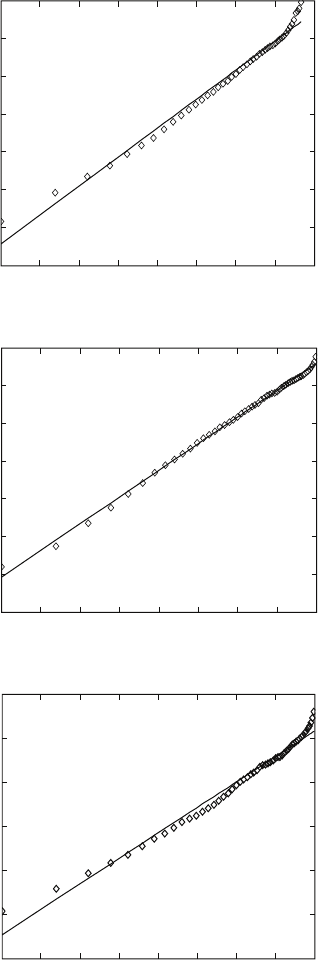
6.11

Plots of ln(ln(1/(1–

))) against ln(

) for deriving the Johnson–

Mehl–Avrami parameters for (a,c,e) Ti-6Al-4V and (b,d,f)

Ti-6Al-2Sn-4Zr-2Mo-0.08Si at different temperatures. (a) Ti-6Al-4V

(750 °C); (b) Ti-6Al-2Sn-4Zr-2Mo-0.08Si (750 °C); (c) Ti-6Al-4V (850 °C);

(d) Ti-6Al-2Sn-4Zr-2Mo-0.08Si (850 °C); (e) Ti-6Al-4V (950 °C); (f) Ti-

6Al-2Sn-4Zr-2Mo-0.08Si (930 °C).



The Johnson–Mehl–Avrami method 143

In(In(1/(1–

)))

–1

–2

–3

–4

–5

0 0.5 1 1.5 2 2.5 3 3.5 4

In(

)

(d) Ti-6Al-2Sn-4Zr-2Mo-0.08Si (850 °C)

In(In(1/(1–

)))

–1

–2

–3

–4

–5

0 0.5 1 1.5 2 2.5 3 3.5 4

In(

)

(e) Ti-6Al-4V (950 °C)

In(In(1/(1–

)))

–1

–2

–3

–4

0 0.5 1 1.5 2 2.5 3 3.5 4

In(

)

(f) Ti-6Al-2Sn-4Zr-2Mo-0.08Si (930 °C)

6.11

Continued



Titanium alloys: modelling of microstructure144

In(In(1/(1–

)))

–1

–2

–3

–4

Data

Best linear fit

750 °C

–1 –0.5 0 0.5 1 1.5 2 2.5 3 3.5 4

In(

)

(a)

In(In(1/(1–

)))

–1

–2

–3

–4

–1 –0.5 0 0.5 1 1.5 2 2.5 3 3.5 4

In(

)

(b)

800 °C

In(In(1/(1–

)))

–1

–2

–3

–4

850 °C

–1 –0.5 0 0.5 1 1.5 2 2.5 3 3.5 4

In(

)

(c)

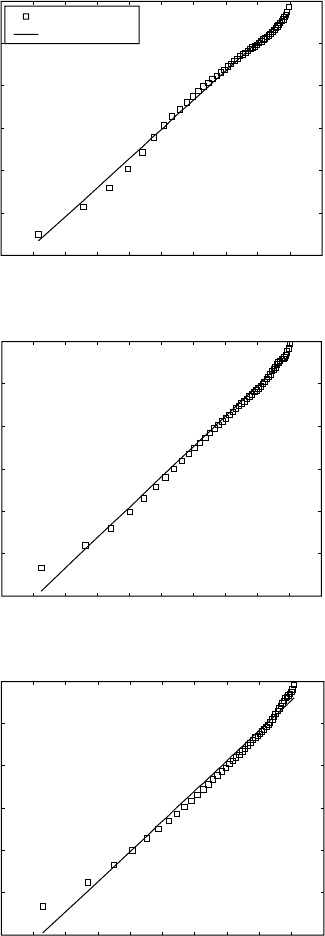
6.12

Plots of ln(ln(1/(1–

))) against ln(

) for deriving the Johnson–Mehl–

Avrami parameters for Ti-8Al-1Mo-1V alloy at different temperatures.

(a) 750 °C; (b) 800 °C; (c) 850 °C; (d) 900 °C; (e) 950 °C; (f) 975 °C.



The Johnson–Mehl–Avrami method 145

In(In(1/(1–

)))

–1

–2

–3

–4

–1 –0.5 0 0.5 1 1.5 2 2.5 3 3.5 4

In(

)

(d)

900 °C

In(In(1/(1–

)))

–1

–2

–3

–4

950 °C

–1 –0.5 0 0.5 1 1.5 2 2.5 3 3.5 4

In(

)

(e)

In(In(1/(1–

)))

–1

–2

–3

–4

–1 –0.5 0 0.5 1 1.5 2 2.5 3 3.5 4

In(

)

(f)

975 °C

6.12

Continued



Titanium alloys: modelling of microstructure146

above cases (Fig. 6.13). For both alloys, there is an abnormality at about

900 °C. Apparently, the transformation can be considered as having two

somewhat different kinetics above and below 900 °C. Within both temperature

intervals and in both alloys, the rate constant increases with decreasing

temperature, i.e. increasing undercooling. Such a characteristic is usual for

phase transformations taking place on cooling. These results are in agreement

with the results from the metallography study of samples after isothermal

exposure at different temperatures (see Sections 6.3.1 and 6.3.2). The

microstructures of the α phase produced above and below 900 °C are different.

For the temperatures above 900 °C, the α phase is mainly grain boundary

nucleated and grown (Fig. 6.4a,b and d). For a high degree of undercooling

(temperatures below 900 °C) (‘Undercooling’ refers to the interval between

the temperature of isothermal exposure and the β transus), mixed mechanisms

of the transformation are observed. The main part is homogeneously nucleated

Table 6.4

Johnson–Mehl–Avrami kinetic parameters for Ti-6Al-

4V and Ti-6Al-2Sn-4Zr-2Mo-0.08Si alloys obtained by ln(ln(1/(1–

))) versus ln(

) plots

Alloy

(°C)

Ti-6Al-4V 950 1.41 0.017

920 1.39 0.024

900 1.21 0.046

870 1.34 0.025

850 1.38 0.022

800 1.34 0.026

750 1.40 0.028

Ti-6Al-2Sn-4Zr-2Mo-0.08Si 930 1.15 0.032

900 1.53 0.014

850 1.53 0.012

800 1.36 0.024

750 1.60 0.013

735 1.30 0.059

Table 6.5

Johnson–Mehl–Avrami kinetic parameters for Ti-8Al-

1Mo-1V alloy obtained by ln(ln(1/(1–

))) versus ln(

) plots

(°C)

750 1.38 0.046

800 1.43 0.036

850 1.43 0.032

900 1.49 0.023

925 1.40 0.025

950 1.44 0.029

975 1.26 0.085



The Johnson–Mehl–Avrami method 147

(within the former β grains) and plate-like grown α phase (Fig. 6.4c,e,f and

g). Small amounts of the grain boundary α are observed as well.

These observations imply that the Avrami index (n values) is different for

the kinetics of the β to α + β transformations above and below 900 °C. As

examples, for grain boundary nucleation after saturation, n = 1, and for

diffusion-controlled growth of plates under the assumption that all particles

are present at t = 0 and have negligible initial dimensions, n = 1.5.

Ti-6Al-4V

, JMA rate constant

0.04

0.035

0.03

0.025

0.02

750 800 850 900 950

(°C)

(a)

Ti-6Al-2Sn-4Zr-2Mo-0.8Si

, JMA rate constant

0.02

0.018

0.016

0.014

0.012

0.01

750 800 850 900 950

(°C)

(b)

6.13

Calculated Johnson–Mehl–Avrami rate constants for β to α + β

transformation in (a) Ti-6Al-4V and (b) Ti-6Al-2Sn-4Zr-2Mo-0.08Si

alloys assuming constant Avrami index (

