Seuront L. Fractals and Multifractals in Ecology and Aquatic Science

Подождите немного. Документ загружается.

214 Fractals and Multifractals in Ecology and Aquatic Science

and Legendre 2003). The existence and the signicance of any potential linear trends were tested

calculating Kendall’s t correlation, which does not require any hypothesis about the characteris-

tics of the original data-set distribution. (Kendall’s coefcient of correlation was used in pref-

erence to Spearman’s coefcient of correlation r because Spearman’s r gives greater weight

to pairs of ranks that are further apart, while Kendall’s t weights each disagreement in rank

equally) (see Sokal and Rohlf 1995 for further developments). We then eventually detrended the

time series, tting linear regressions to the original data by least squares, and used the regres-

sion residuals in further analysis. The purpose of this is to eliminate aliasing in further analysis

due to large-scale structures present in the data sets, such as in monotonically increasing or

decreasing trends.

In order to provide direct comparisons between the different parameters investigated here, the

time observations, x

, were converted into normalized, dimensionless descriptors, y

, following:

−

min

maxmin

(6.17)

where x

max

and x

min

are the maximum and minimum values of the series, respectively. Samples of

the resulting time series are given in Figure 6.10, and the Packard-Takens, largest Lyapunov expo-

nents, and correlation integral methods were used to investigate their properties.

table 6.1

tidal Velocity (m s

–1

) and direction (dir, °), water column depth (m) and mean Values

of temperature (°c), salinity (Psu), and In Vivo Fluorescence (Fluorescence relative

units) for the 24 studied data sets

tidal current

speed dir (°) depth t s F

S1 0.55 240 21.56 6.55 34.60 18.32

S2 0.45 220 22.49 6.53 34.60 15.20

S3 0.10 60 27.38 6.51 34.62 10.90

S4 0.95 15 28.28 6.50 34.66 9.39

S5 0.90 10 26.21 6.49 34.70 8.23

S6 0.15 10 23.25 6.51 34.65 10.25

S7 0.32 260 21.52 6.53 34.61 15.02

S8 0.62 230 22.21 6.52 34.62 17.24

S9 0.10 85 27.19 6.50 34.65 11.45

S10 0.98 10 28.47 6.49 34.72 6.80

S11 1.00 10 26.53 6.49 34.67 7.29

S12 0.30 10 23.66 6.50 34.64 11.00

S13 0.35 290 21.38 6.53 34.62 17.40

S14 0.30 200 21.72 6.55 34.62 15.82

S15 0.11 140 26.19 6.52 34.66 13.46

S16 0.80 10 28.65 6.50 34.69 10.75

S17 1.10 10 27.15 6.49 34.70 6.64

S18 0.40 10 24.15 6.51 34.68 7.35

S19 0.35 260 21.75 6.53 34.63 12.64

S20 0.87 250 21.68 6.55 34.62 17.69

S21 0.73 230 25.23 6.55 34.61 15.16

S22 0.18 10 28.65 6.53 34.71 8.30

S23 1.04 10 27.50 6.50 34.66 5.37

S24 0.60 10 25.95 6.50 34.62 3.87

2782.indb 214 9/11/09 12:13:23 PM

Fractal-Related Concepts: Some Clariﬁcations 215

6.1.3.3.3 Results

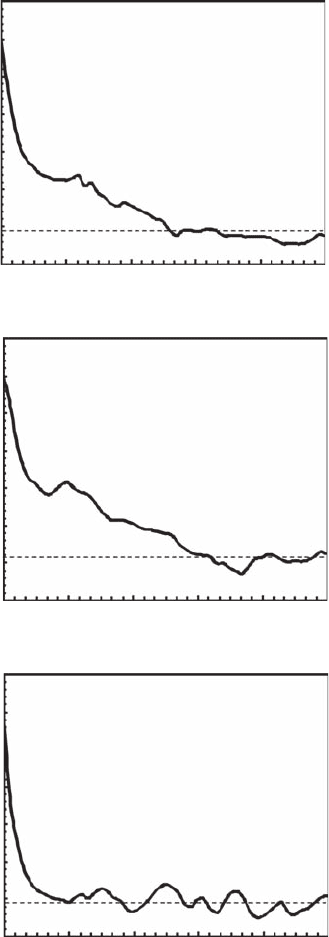
The delay time t has been chosen as the decorrelation time of the time series (Tsonis et al. 1993) as

75, 95, and 30 seconds for temperature, salinity, and in vivo uorescence time series, respectively

(Figure 6.11). This delay time was also used for the following calculations of Lyapunov exponents

and correlation dimensions.

Temperature

Time (seconds)

SalinityIn vivo Fluorescence

1.0

0.8

0.6

0.4

0.2

0.0

1.0

0.8

0.6

0.4

0.2

0.0

1.0

0.8

0.6

0.4

0.2

0.0

500 1000 1500 25002000 3000

Time (seconds)

0 500 1000 1500 25002000 3000

Time (seconds)

0 500 1000 1500 25002000 3000

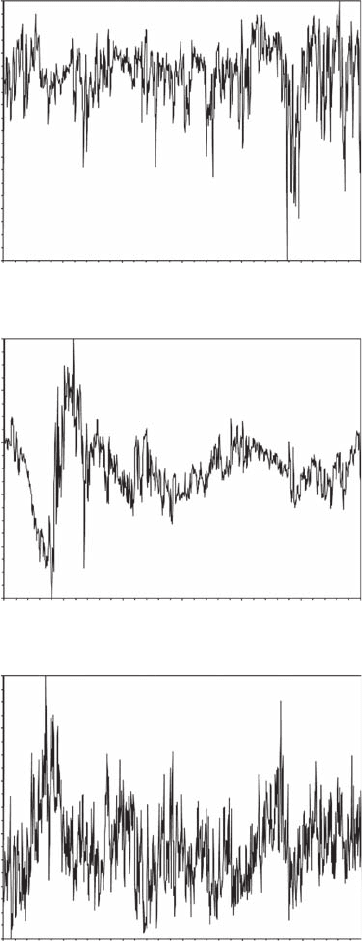
Figure 6.10 Samples of normalized temperature (A), salinity (B), and in vivo uorescence (C) time series

recorded in the inshore waters of the eastern English Channel; shown for data set S1. (Modied from Sueront,

2004.) (Kraichnan, R.H., 1967), Inertial ranges in two-dimensional turbulence, Physics of Fluids, 10, 1417–1423.

2782.indb 215 9/11/09 12:13:26 PM

216 Fractals and Multifractals in Ecology and Aquatic Science

The three-dimensional phase-space portraits of the attractors produced by the Packard-Takens

method did not clearly exhibit any attractor (Figure 6.12). Note, however, the differences between

the phase-space portraits of uorescence on the one hand and temperature and salinity on the other

hand. The phase-space portraits for temperature and salinity appear as somewhat elongated and

Lag Time h (seconds)

Autocorrelation

1.2

1.0

0.8

0.6

0.4

0.2

–0.2

0.0

30 60 90 150120

0306090 150120

Autocorrelation

1.2

1.0

0.8

0.6

0.4

0.2

–0.2

0.0

Autocorrelation

1.2

1.0

0.8

0.6

0.4

0.2

–0.2

0.0

Figure 6.11 Autocorrelation functions r(h) of temperature (A), salinity (B), and in vivo fluorescence

dashed line is the special case r(h) = 0 leading to the decorrelation time of the time series.

2782.indb 216 9/11/09 12:13:28 PM

Fractal-Related Concepts: Some Clariﬁcations 217

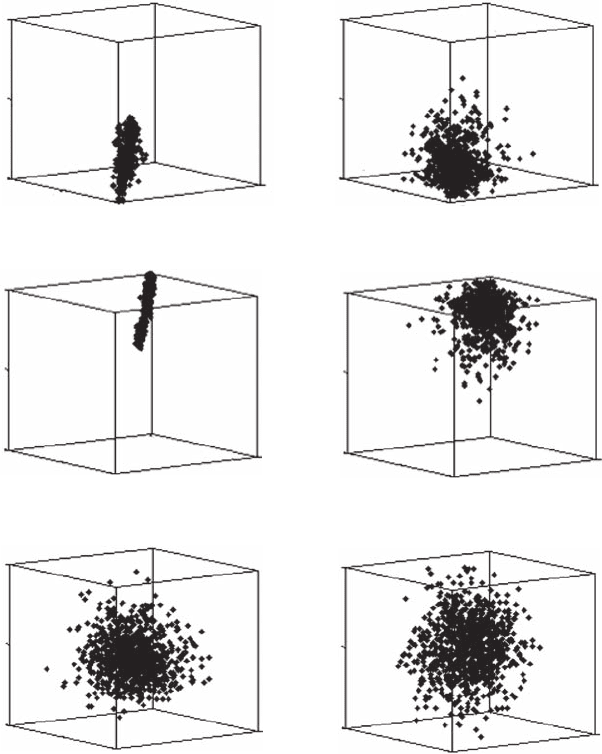
relatively narrow spatial distributions (Figure 6.12A,B). Phase-space trajectories of in vivo uo-

rescence, however, did not exhibit any characteristic shape, suggesting a more space-lling—or

“random”—behavior (Figure 6.12C). Moreover, comparison of phase-space portraits obtained from

time series recorded in high and low hydrodynamic conditions leads to further results. Phase-space

trajectories of temperature and salinity then appear clearly more structured in lower hydrodynamic

conditions (Figure 6.12D,E), while the apparent randomness of in vivo uorescence phase-space

trajectories remains whatever the hydrodynamic conditions (Figure 6.12F).

The largest Lyapunov exponents, LLE, l

, calculated over a range of embedding dimensions E

exhibit clearly different behaviors (Figure 6.13). By embedding dimension 8, the temperature and

salinity LLE converge to positive values that are larger when the hydrodynamic conditions are high

(Figure 6.13A,B). In other words, the higher the hydrodynamic conditions, the larger the positive

exponent, the more chaotic the system, and the shorter the time scale of system predictability (Wolf

et al. 1985). This is conrmed by the signicant negative correlation between largest Lyapunov

t+150

0.5

t+150

0.5

t+75

0.5

t+75

0.5

t+75

0.5

t+75

0.5

t+75

0.5

t+75

0.5

t+150

0.5

t+150

0.5

t+150

0.5

t+150

0.5

Figure 6.12 Three-dimensional phase-space portraits of normalized temperature, salinity, and in vivo

uorescence time series. (A, B, C) represent conditions of low hydrodynamic conditions for data set S3, and

(D, E, F) represent conditions of high hydrodynamic conditions for data set S17.

2782.indb 217 9/11/09 12:13:31 PM

218 Fractals and Multifractals in Ecology and Aquatic Science

Largest Lyapunov Exponent λ

0.5

0.4

0.3

0.2

0.1

0.0

Largest Lyapunov Exponent λ

0.5

0.4

0.3

0.2

0.1

0.0

Largest Lyapunov Exponent λ

0.5

0.4

0.3

0.2

0.1

0.0

01 2 3 456 7 8 9 10 11

Embedding Dimension E

01 2 3 456 7 8 9 10 11

Embedding Dimension E

0 1 2 3 456 7 8 9 10 11

Embedding Dimension E

Figure 6.13 The largest Lyapunov exponent l

estimated for temperature (A), salinity (B), and in vivo

uorescence (C) time series under high (open diamonds: S15) and low (black diamonds: S23) hydrodynamic

conditions. The dashed and dotted lines in (A, B) indicate the convergent values of l

under low and high

hydrodynamic conditions, respectively. (Kraichnan, R.H., 1967, Inertial ranges in two-dimensional turbu-

lence, Physics of Fluids, 10, 1417–1423.)

2782.indb 218 9/11/09 12:13:33 PM

Fractal-Related Concepts: Some Clariﬁcations 219

exponents of both temperature and salinity, and tidal current speed direction. The largest Lyapunov

exponents and the associated time scale of predictability are shown in Table 6.2. In contrast, uores-

cence LLE remain signicantly higher than temperature and salinity LLE irrespective of the hydro-

dynamic conditions, but never converge to any constant value, even when the embedding dimension

E is increased up to 10 (Figure 6.13C). This indicates more chaotic behavior and less predictability

in phytoplankton biomass than in temperature and salinity uctuations.

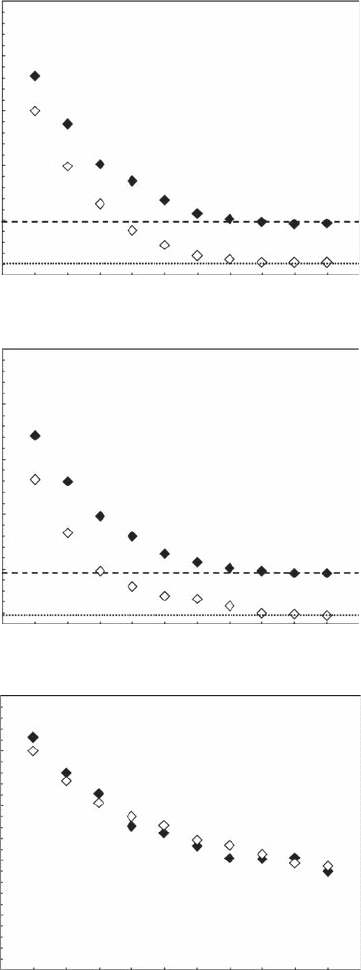
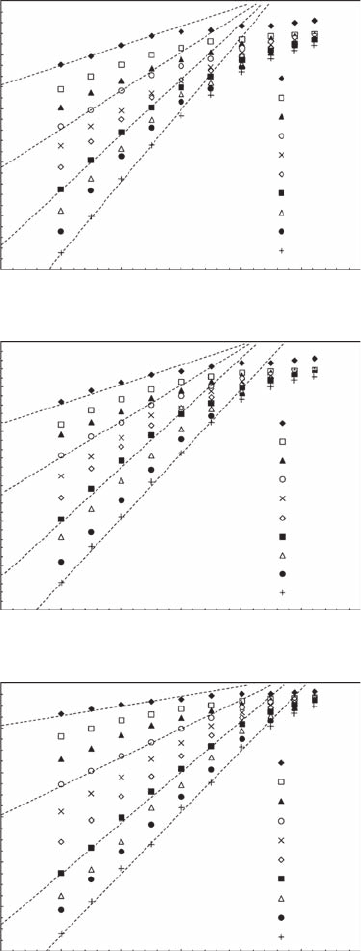
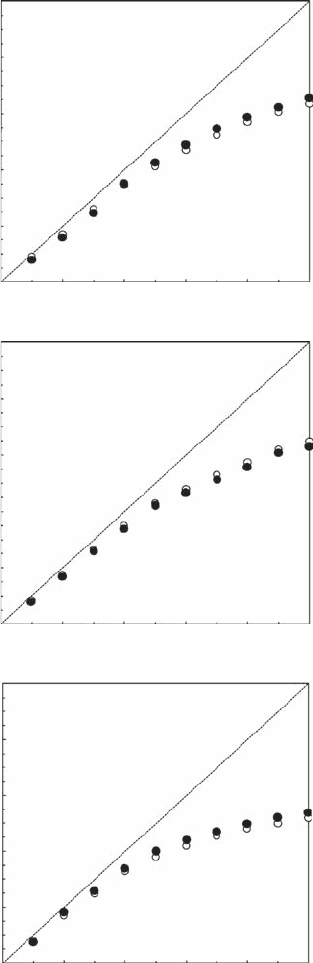
Figure 6.14 shows the correlation integral C(r) on logarithmic scales as a function of distance

r by varying embedding dimension E from 1 to 10. Estimates of the correlation dimension v (see

Equation 6.15) for temperature and salinity did not converge to any constant value whatever the

hydrodynamic conditions (Figure 6.15A,B) and indicate the lack of empirical evidence for deter-

ministic chaos. Moreover, no signicant differences were observed between temperature and salin-

ity correlation dimensions, or between the different time series for either parameter, suggesting very

similar behaviors of temperature and salinity time series in phase-space. The results for in vivo uo-

rescence time series are very similar with those of temperature and salinity. Clearly no saturation,

table 6.2

largest lyapunov exponents l

estimates for temperature, salinity, and in vivo Fluorescence

from the 24 available data sets, and the related time scale of system Predictability

Predictability (seconds)

t s F* t s F

S1 0.048 0.045 0.212 20.83 22.22 4.72

S2 0.044 0.043 0.223 22.73 23.26 4.48

S3 0.012 0.009 0.225 83.33 111.11 4.44

S4 0.098 0.105 0.243 10.20 9.52 4.12

S5 0.092 0.094 0.172 10.87 10.64 5.81

S6 0.021 0.023 0.221 47.62 43.48 4.52

S7 0.031 0.035 0.236 32.26 28.57 4.24

S8 0.055 0.057 0.198 18.18 17.54 5.05

S9 0.011 0.009 0.217 90.91 111.11 4.61

S10 0.091 0.088 0.171 10.99 11.36 5.85

S11 0.095 0.084 0.223 10.53 11.90 4.48

S12 0.038 0.039 0.181 26.32 25.64 5.52

S13 0.041 0.039 0.234 24.39 25.64 4.27

S14 0.042 0.039 0.182 23.81 25.64 5.49

S15 0.012 0.016 0.234 83.33 62.50 4.27

S16 0.076 0.079 0.172 13.16 12.66 5.81

S17 0.121 0.133 0.228 8.26 7.52 4.39

S18 0.038 0.041 0.196 26.32 24.39 5.10

S19 0.032 0.034 0.253 31.25 29.41 3.95

S20 0.085 0.088 0.228 11.76 11.36 4.39

S21 0.076 0.074 0.234 13.16 13.51 4.27

S22 0.025 0.017 0.254 40.00 58.82 3.94

S23 0.097 0.096 0.174 10.31 10.42 5.75

S24 0.071 0.075 0.187 14.08 13.33 5.35

Mean 0.056 0.057 0.212 28.53 30.06 4.79

SD 0.032 0.033 0.027 24.36 28.84 0.64

Min 0.011 0.009 0.171 8.26 7.52 3.94

Max 0.121 0.133 0.254 90.91 111.11 5.85

Following the absence of convergent behavior for the uorescence Lyapunov exponents, we report here the

estimated

for E = 10.

2782.indb 219 9/11/09 12:13:34 PM

220 Fractals and Multifractals in Ecology and Aquatic Science

0.0

E = 1

E = 2

E = 3

E = 4

E = 5

E = 6

E = 7

E = 8

E = 9

E = 10

E = 1

E = 2

E = 3

E = 4

E = 5

E = 6

E = 7

E = 8

E = 9

E = 10

E = 1

E = 2

E = 3

E = 4

E = 5

E = 6

E = 7

E = 8

E = 9

E = 10

–0.5

–1.0

Log C (r)

–1.5

–2.0

–2.5

0.0

–0.5

–1.0

Log C (r)

–1.5

–2.0

–3.0

–2.5

–2.0

–3.0

–4.0

–6.0

–5.0

–1.0

0.0

–1.2 –1.0 –0.8 –0.6 –0.4 –0.2 0.0

Log r

–1.2 –1.0 –0.8 –0.6 –0.4 –0.2 0.0

Log r

–1.2 –1.0 –0.8 –0.6 –0.4 –0.2 0.0

Log r

Figure 6.14 Log-log plots of correlation integral C(r) versus distance r for various embedding dimensions E

for temperature (A), salinity (B), and in vivo uorescence (C) time series; shown for database S8. (Kraichnan,

R.H., 1967, Inertial ranges in two-dimensional turbulence, Physics of Fluids, 10, 1417–1423.)

2782.indb 220 9/11/09 12:13:38 PM

Fractal-Related Concepts: Some Clariﬁcations 221

Correlation Dimension v

246

Embedding Dimension E

810

Correlation Dimension v

246

Embedding Dimension E

810

Correlation Dimension v

246

Embedding Dimension E

810

Figure 6.15 Correlation dimensions v vs. embedding dimensions E for temperature (A), salinity (B), and

in vivo uorescence (C) under high (open diamonds; dataset S15) and low (black diamonds; data set S23)

hydrodynamic conditions. (Kraichnan, R.H., 1967, Inertial ranges in two-dimensional turbulence, Physics of

Fluids, 10, 1417–1423.)

2782.indb 221 9/11/09 12:13:42 PM

222 Fractals and Multifractals in Ecology and Aquatic Science

and therefore no evidence of low-order deterministic chaos, exists whatever the hydrodynamic con-

ditions (Figure 6.15C). As previously shown for temperature and salinity time series, no signicant

differences exist between the correlation dimensions v. These results conrm the previous lack of

convergence of uorescence LLE (see Figure 6.13C), and indicate that there is no evidence for deter-

ministic chaos in the temporal uctuations of phytoplankton biomass time series.

6.1.3.3.4 Discussion

6.1.3.3.4.1 Phase-Space Portraits

The Packard-Takens method is probably the fastest and most direct method to infer the potential

existence of deterministic chaos. Creating the phase-space attractor of a system with a computer

is a very simple task. All that is needed is the copy of the data le, paste it shifted by one, two, or

more places, and plot the data. Thus, a subjective assessment of the “degree of randomness” can be

reached almost instantaneously from this kind of plot. It is nevertheless stressed that the charac-

teristic shape of the attractor is not easy to describe in simple terms. Figure 6.12 shows projections

of phase-space trajectories onto three-dimensional space, so that the fact that no attractors can be

seen does not imply that they do not exist when embedding in higher-dimensional space. However,

a strange attractor of higher-dimensional space often reects its shape onto the lower-dimensional

space as well. For instance, the trajectory onto the two-dimensional phase-space (embedding dimen-

sion E = 2 in Equation 6.10), reconstructed from the time series of variable x of the Lorenz equa-

tions, shows a clear strange attractor (Figure 6.8B). These results can then instead be regarded as a

qualitative prerequisite analysis and demonstrate that inferring the existence of any deterministic

structure beyond the highly uctuating behavior exhibited by temperature, salinity, and in vivo

uorescence time series (Figure 6.10) is a far more difcult task.

6.1.3.3.4.2 Largest Lyapunov Exponents

The LLE estimates quantitatively conrm the subjective results of the Packard-Takens method, that

is, a lower-dimensional behavior in low hydrodynamic conditions for temperature and salinity time

series, and a higher-dimensional behavior for phytoplankton biomass time series that did not exhibit

any convergent behavior of their LLE for values of the embedding dimension E up to 10 irrespec-

tive of the hydrodynamical conditions. What may be regarded as being very important for ecolo-

gists is that, unlike fractal dimensions, Lyapunov exponents remain well dened in the presence

of dynamical noise and can be estimated by methods that explicitly incorporate noise (Ellner et al.

1991; Nychka et al. 1992). This leads us to consider that estimating Lyapunov exponents is the best

approach for detecting chaos in ecological systems (Hastings et al. 1993). A number of limitations

in Lyapunov exponent estimates to detect deterministic chaos can, however, be raised and regards

both estimate accuracy and the minimum number of data points required in the analysis.

First, although the algorithm used in this chapter (Wolf et al. 1985) provides a good estimation

of the largest Lyapunov exponents for noise-free, synthetically generated time series from cha-

otic dynamics, the estimation for experimental time series is still relatively imprecise (Rodriguez-

Iturbe et al. 1989). Second, it has been stressed that to detect a chaotic attractor of dimension 3, at

least 1,000 to 30,000 data points are needed (Wolf et al. 1985), while others (Ramsey and Yuan

1989) found that 5,000 data points is a lower bound for the detection of chaos on some simple

dynamical systems known to display chaotic behaviors in certain regimes. Moreover, Vassilicos et

al. (1993) demonstrated how the tests for chaos can give positive answers—for example, positive

Lyapunov exponents—when subsamples with a smaller number of data points are used, and how

these Lyapunov exponents converge to zero when the number of data points is increased.

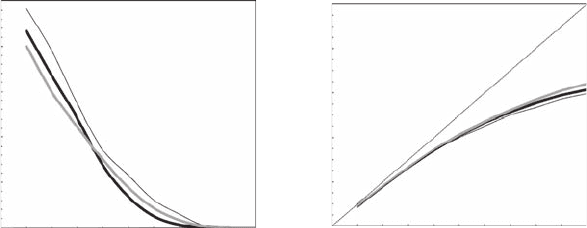
The latter limitation has been specied through estimates of the largest Lyapunov exponents of

the larger original time series (that is, 172,800 data points) of temperature, salinity, and in vivo uo-

rescence that were divided into 24 subsections of 7,200 points in the present work. Subsequent results

(Figure 6.16A) then indicated that LLEs of temperature, salinity, and phytoplankton biomass time

2782.indb 222 9/11/09 12:13:43 PM

Fractal-Related Concepts: Some Clariﬁcations 223

series remain positive but converge to zero. As previously mentioned, a positive largest Lyapunov

exponent indicates chaotic dynamics, but values quite close to zero should therefore only be inter-

preted as an order of magnitude. As a consequence, the different convergent positive values of the

different LLEs estimated for temperature and salinity time series in high and low hydrodynamic

conditions (Figure 6.13A,B) suggest a phenomenological shift between low-dimensional chaos and

high-dimensional stochasticity as the one observed by Ruelle and Takens (1971) near the transition

to turbulence. Alternatively, a positive largest Lyapunov exponent close to zero can be interpreted

as having been derived from a stochastic time series with many degrees of freedom (Jeong and Rao

1996). More generally, systems with a Lyapunov exponent of zero are associated with a state called

the edge of chaos, where complex behavior is the rule. The exact meaning of the edge of chaos

depends on the context within which it is used but, roughly speaking, it describes the vicinity of

some instability point separating a region of more ordered (or less random) behavior from a region

of less ordered (or more random) behavior. The edge of chaos has attracted considerable interest

among biologists and ecologists because processes such as evolution or adaptive behavior have

been precisely shown to be just at the edge of chaos (Kauffman and Johnson 1991; Langdon 1992;

Kauffman 1993). Such a critical state would increase the adaptive efciency of a given system—for

instance, in response to uctuating environmental conditions—and could then be of prime interest

in the future understanding of ecosystem functioning.

6.1.3.3.4.3 Correlation Integrals

Although it has been shown that if the data set is small, the correlation dimension v (see Equation

6.15) appears to converge toward a nite value even in the absence of chaos (Smith 1988), this

is obviously not the case here (Figure 6.15). Moreover, correlation dimension v estimates for the

172,800 data-point time series (Figure 6.16B) did not converge to any constant value and conrm

the lack of empirical evidence for deterministic chaos previously shown with smaller time series

(Figure 6.15). Our results then cannot be associated with sampling limitation. A correlation dimen-

sion of 2 has thus been identied on the basis of a 1,200 values of chlorophyll transect recorded

in the central waters of the Ligurian Sea (NW Mediterranean Sea; Ibanez 1986). This result

then conrms the efciency of the correlation algorithm to detect low deterministic chaos when

applied to small data sets. This also conrms that different hydrodynamic conditions might be

at the origin of differential space-time structures, in terms of low-order deterministic chaos or

high-order stochasticity. Then, high hydrodynamic conditions, such as those occurring in the

eastern English Channel, could be at the origin of temperature, salinity, and phytoplankton

0.5

0.4

0.3

0.2

0.1

0.0

Largest Lyapunov Exponent λ

Embedding Dimension E

012345678910

Correlation Dimension v

Embedding Dimension E

012345678910

Figure 6.16 The largest Lyapunov exponent l

(A) and correlation dimensions v (B) plotted against embed-

ding dimensions E for temperature (thick black line), salinity (thick gray line) and in vivo uorescence (thin

black line) from the original 172,800 data points time series. The dashed line is the correlation dimensions v

expected for an uncorrelated noise (B).

2782.indb 223 9/11/09 12:13:47 PM