Семиохин И.А., Страхов Б.В., Осипов А.И. Кинетика химических реакций
Подождите немного. Документ загружается.

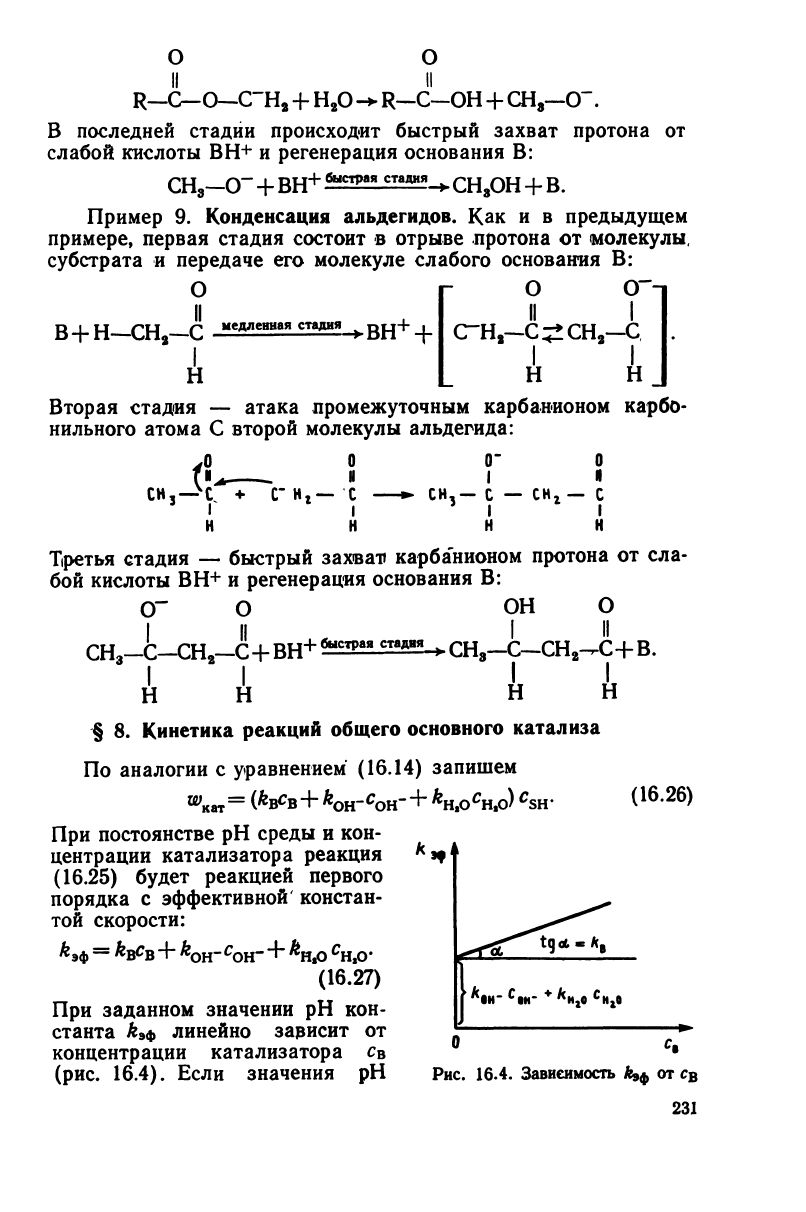
R—С—
О—(ГН
8
+
Н
г
О
-*-
R—С—ОН
+
СН,—СТ.
В
последней стадии происходит быстрый захват протона от
слабой
кислоты
ВН+
и регенерация основания В:
СН
8
—О~
+
ВН+
быстр
"'
стадия
-».
CH
S
OH
+
В.
Пример
9. Конденсация альдегидов. Как и в предыдущем
примере, первая стадия состоит в отрыве протона от молекулы,
субстрата
и передаче его молекуле слабого основания В:
О
II
В+Н—СН,—С
А
медленная стадия
-ВН+
+
(ГН,—С;
А
ОГ-]
:сн
3
—с
н
Вторая
стадия — атака промежуточным карбанионом карбо-
нильного атома С второй молекулы альдегида:
О
н
г
н
г
—
с
I
н
О"
I
II
СН,—
С —
СН
г
— С
Третья стадия — быстрый захват карбанионом протона от сла-
бой
кислоты
ВН+
и регенерация основания В:
О"
О ОН О
СН
3
-С-СН
2
-С+ВН+
быстрая стадия
>
СН
8
-С-СН
2
^С+В.
§
8. Кинетика реакций общего основного катализа
По
аналогии с уравнением
(16.14)
запишем
При
постоянстве рН среды и кон-
центрации катализатора реакция
(16.25)
будет реакцией первого
порядка с эффективной констан-
той
скорости:
(16.27)
При
заданном значении рН кон-
станта
&ЭФ
линейно заэисит от
концентрации катализатора с
в
(рис. 16.4).
Если значения рН
*и
2
о
с
и
г
о
Рис.
16.4. Зависимость &>*
от
с
в
231

меняются, определяют зависимость к
эф
от
рН(с
ои
~)
и получа-
ют из прафиков отдельные значения констант скорости
*в» ^он"
и
*н
а
о-
§
9. Соотношения Бренстеда
Для
общего кислотного и основного катализа. Бренстедом
были установлены корреляционные соотношения между кон-
стантами скорости и соответствующими константами ионизации
Кал
катализирующих кислот и константами основности Къл ка-
тализирующих оснований:
a,i
k
Bti
=
const
Kb.
(16.28)
Эти
соотношения
получили
название
соотношений
Бренсте-
да.
Если
а=0,1,
катализатором является растворитель; ско-
рость реакции в этом случае слабо возрастает в; растворах да-
же
относительно сильных кислот. Если же
а=0,5,
реакции в бу-
ферных растворах ускоряются, в основном под действием не-
диссоциированных слабых кислот, т. е. налицо случай общего
кислотного катализа. Наконец, если а=1, каталитическое дей-
ствие буфера почти целиком определяется содержащимися в
нем ионами гидроксония, т. е. реакция может быть отнесена
к случаю специфического кислотного катализа.
Аналогичные
выводы
по значениям показателей р в урав-
нении
(16.28)
могут быть применены и к основному катализу.
При
постоянной энтропийной составляющей из соотношений
Бренстеда
следует корреляция «между энергиями активации и
тепловыми эффектами реакций:
Е
а
=
const+а (р) Д#. (16.29)
Подобная
корреляция была получена Хориути и Поляни при
сопоставлении потенциальных диаграмм различных реакций и
использовании теории активированного, комплекса.
Исследуя
реакции радикалов, Семенов пришел к подобным
соотношениям для экзотермических реакций:
£
0
=
48,1+ 0,25
ДЯ>Дж/моль,
(16.29а)
где £
0
— высота потенциального барьера реакции, и для эн-
дотермических реакций:
Е
в
=
48,1
+
0,75
ЛЯ кДж/моль.
(16.296)
232

Глава
17
ГЕТЕРОГЕННЫЕ
КАТАЛИТИЧЕСКИЕ
РЕАКЦИИ
§
1. Процессы активации
Любая
гетерогенная каталитическая реакция включает в
себя
несколько последовательно идущих стадий. Обычно она
начинается с диффузии реагирующих веществ к поверхности
катализатора (внешняя диффузия) и
внутрь
его лор (внутрен-
няя диффузия).
Затем
следует адсорбция и сама реакция на
поверхности катализатора (в зависимости от ее состояния —
на внешней или внутренней поверхности).
После
этого проис-
ходит
десорбция и транспорт продуктов реакции от поверхно-
сти
катализатора в объем. Скорость такой сложной реакции
определяется
скоростью
более
медленной стадии.
Катализаторы не вызывают, а ускоряют химические реак-
ции. Ускорение каталитических реакций, (см. рис.
16.1),
обу-
словлено снижением энергии активации по сравнению с энер-
гией активации некаталитической реакции.
Рассмотрим
возможные пути
некоторой гомогенной реакции
без
катализатора и на поверхно-
сти
катализатора (рис. 17.1) без
учета диффузионных процессов.
Из
рисунка видно, что
U
(17.1)
реакч
(17.2)
Пути
реакции
Рис.
17.1. Возможные пути гомо-
генной каталитической реакции
(сплошные
кривые)
и гетерогенной
каталитической реакции (пунктир-
ные
кривые)
В
этом случае (без учета диф-
фузии)
ускорение реакции
обус-
ловлено экзотермическим харак-
тером адсорбции активирован-
ного комплекса на твердом катализаторе. Однако, как видно
из
уравнения
(17.2),
ускорение зависит также от отношения
2гег.каж/2гом> пропорционального числу активных центров на
поверхности катализатора.
Ясно,
что число активных центров
меньше числа адсорбционных центров на поверхности носите-
ля и катализатора и зависит от природы и
способа
приготов-
ления катализатора.
§
2. Кинетические уравнения элементарных реакций
Мерой
каталитической активности обычно считается удель-
ная (на единицу поверхности) скорость (или, что то же
самое,
константа скорости) исследуемой реакции.
233

Без
учета диффузии в гетерогенных каталитических реак-
циях роль одного из реагирующих веществ играет адсорбцион-
ный центр. Поэтому для адсорбции некоторого вещества А:
А
(газ)+1
аде. центр = А
(аде),
(17.3)
согласно
основному постулату химической кинетики,
(17.4)
Здесь
РА
— парциальное давление вещества А в газовой
фазе,
6о
— доля свободной поверхности.
Аналогично, для процесса
(17.3)
скорость десорбции будет
равна
О>дес
=
*десе
А
,
О
7
'
5
)
где 6л — доля поверхности, занятой веществом А.
Рассмотрим
теперь химическую реакцию в хемосорбцион-
ном
слое:
*А
(aAc)
+
v
2
A
2
(адс)+
... =v|B
1
(адс)+
....
(17.6)
ЕЬли
все молекулы А,- занимают одинаковое число адсорбци-
онных центров, а молекулы B
t
—
тоже
одинаковое (но другое
и
большее, чем А/) число адсорбционных центров, то превра-
щение в хемосорбционном слое возможно при
наличии
недоста-
ющего числа свободных центров адсорбции:
An=Sv:—2v
£
.
(17.6a)
Уравнение
(17.6)
в этом случае следует переписать в виде
v^!
(аде)
+ ... +
Дл
(своб.
аде. центров) =
v[
Ъ
г
(аде)
+ ... .
(17.7)
Скорость гетерогенной каталитической реакции, по опреде-
лению, есть изменение количества реагента А/ в единицу вре-
мени на единице! площади поверхности катализатора:
•*—-Нг-
(178)
где S — общая площадь поверхности катализатора, на кото-
рой происходит химическая реакция.
Согласно основному постулату химической кинетики, ско-
рость гетерогенной реакции пропорциональна произведению по-
верхностных концентраций реагирующих веществ и свободных
активных центров, взятых в степенях, равных стехиомегриче-
ским коэффициентам, если реакция
(17.7)
протекает в одну
стадию.
Поверхностные
концентрации реагентов и активных центров
пропорциональны доле поверхности, приходящейся на соответ-
234

ствующие вещества 6/ и свободные активные центры 6о- По-
этому
для реакции
(17.7)
в расчете на единицу площади по-
верхности (S=l) получим
w =
kJfil
g
...Q$*
(17.9)
для прямого процесса и
ш
= ^-
1
вз|..
(17.10)
для обратного процесса. В последнем случае не учитывается
множитель бо", поскольку в правой части уравнения
(17.7)
не фигурируют активные центры. Если же
Дл<0,
множитель
Go
n
появится в уравнении
(17.10)
и исчезнет из уравнения
(17.9).
При
сопоставлении уравнений
(17.4)
и
(17.5)
с уравнения-
ми
(17.9)
и
(17.10)
видна аналогия между процессами адсорб-
ции и химическими реакциями в хемосорбционном
слое.
Для
неоднородных ^поверхностей каждому типу центров ад-
сорбции соответствует отдельное уравнение вида
г
1
А
1
+
Дл(адс.
центр типа
0=
v
'
B
i+--
.
(17.11)
В
этом случае общая скорость прямого процесса будет равна
(17.12)
а
общая скорость обратного процесса равна соответственно
(17.13)
§
3. Кинетические уравнения химических реакций на
однородных поверхностях
Если адсорбционные процессы происходят быстро, величи-
ны 6л| и 0о можно
вычислить
из уравнений адсорбционного
равновесия:
где
Ь
— адсорбционные; коэффициенты.
Если реакция происходит в одну стадию типа
(17,7),
то из
уравнения
1(17.12)
получим
235

w-
(17.15)
В
простейшем случае, когда
А
(аде)-*-В
(аде),
Дя
=
0,
получаем
^(17.16)
При
слабой адсорбции продуктов реакции
(Ьв/0в<1)
по ме-
ре увеличения сорбируемости исходного вещества А порядок
реакции по веществу А снижается от 1 до 0. В этом случае
из
уравнения
(17.16)
можно получить три частных случая:
а) при
bjj)
A
<
1
w =
kbjj)
A
;
(17.16а)
б) при
bjj)
A
~ I w = k
t
ЬАРА
; (17.166)
1
+
VA
в) при Ь
А
Р
А
»
1
» =
*•
(17.16B)
Эффективная
кажущаяся энергия активации Е
кат
повы-
шается
при этом от
Е
ИС
т—ЯА
ДО
£
И
СТ,
где
ЛА
— теплота адсорб-
ции вещества А.
При
средней адсорбции продукта реакции В, т. е. при зна-
чении &вРв~1, кинетические уравнения усложняются и прини-
мают вид
г)при6
А
р
А
<1
w
=
k
Д
А
;
(17.16г)
1
+
VB
д)
при &АРА~
1
w=k
А х
,
(17.16д)
• ^
А^А ' В^В
е)
при 6АРА>
1
w=k.
(17.16e)
Наконец,
при сильной адсорбции продукта реакции В, ког-
да
&вр
в
»
1
+
Ьдр
А
,
получаем одно уравнение вида
(17.16ж)
Рассмотрим
теперь случай, когда скорость всего 'процесса
определяется
скоростью адсорбции одного лз исходных ве-
236

ществ,
например, вещества А
г
. Общая скорость реакции будет
раЬна скорости адсорбции этого вещества:
w = w
am
^kp
At
%.
(17.17)
Трудной задачей в таком случае будет вычисление
величины
во,
поскольку нельзя использовать уравнение изотермы ад-
сорбции.
Если
адсорбируемостью А
{
можно пренебречь,
величину
0
О
можно
определить по изотермам других веществ. Тогда
выра-
жение
для скорости реакции- запишется в виде
w^w^k
Р
-Ь
(17.18)
Если
адсорбируемостью А] пренебречь нельзя, решение
уравнения
(17.17)
можно (получить только при небольшом сме-
щении от положения равновесия. Тогда можно представить,
что в хемосорбционном слое в каждый момент времени уста-
навливается химическое равновесие, отвечающее стационарно-
му значению 6
Al
и равновесным значениям в
А,
...
вв,...
•
Концентрации реагирующих веществ изменяются по мере из-
менения стационарных
величин
0A
t
.
В
этом случае из условий химического адсорбционного рав-
новесия
«методом последовательных приближений определяют
квазистационарные значения
6
Al9
а затем и значение во,
необ-
ходимое
для решения уравнения
(17.17).
§
4. Кинетические уравнения химических реакций на
неоднородных поверхностях
Рассмотрим
каталитическую реакцию вида
А
1
(адс)
+
А
а
(газ)+
...
=8^33)+
...,
(17.19)
в которой учитывается только адсорбция вещества к\.
Для
однородной поверхности скорость элементарной реак-
ции можно записать как
...
(17.20)
Для
неоднородной поверхности необходимо провести сум-
мирование таких выражений для каждого типа участков по-
верхности,
характеризуемых своими теплотами адсорбции h:
РА,
... 2 kfi^Vt-PA.... 2
-TXT-IPI-
(17.21)
1
l +
biP
Здесь
(17.22)
относительная доля центровгадсорбция t-ro типа и
p=p
At
.
237

Для
«аморфных» поверхностей Лангмгор использовал прфде
ставление о непрерывном распределений центров и теплот ад-
сорбции.
В этом случае вероятность того, что для произволь-
ного центра теплота адсорбции равна
%
с точностью до dK
9
бу-
дет
равна
dW(X)=?(k)dX.
(17.23)
Скорость реакции
(17.19)
можно переписать в виде
(17.24)
Это
уравнение можно решить только в случае, когда k(k) од-
нозначно и непрерывно зависит от теплоты адсорбции.
Если
к(%) и р(А,) —
непрерывные
функции, можно ввести
вспомогательную непрерывную функцию F(K), равную
F(K)
=
k(X)p{K)
9
(17.25)
что
дает
возможность привести выражение
(17.24)
к виду
Х
макс
мак
V
J
(17.26)
Решение
этого уравнения выполняется подбором функций
F
(К).
Так, дробный порядок реакции, когда
Я>(РА
|
)
=
*Р
1/П
. (17.27)
получается при подстановке F(X) в виде
F (\)
=
k (Я)
о
(К)
=
const
e-*/**
r
. (17.28)
При
рассмотрении различных функций р(Х) предпочтение
отдают
экспоненциальному или гауссовому распределению око-
ло
одного или нескольких значений Аои- При экспоненциальном
распределении наблюдается изотерма адсорбции
Фрейндлих
а:
e
=
constp
1
/'"
(17.29)
и
выполняется кор(реляционное соотношение Бренстеда:
£|
=
const/(?,
где
а=
1/2—
1/т, т>2.
(17.30)
§
5. Роль диффузии в кинетике гетерогенных
каталитических реакций
В
реальных гетерогенных каталитических процессах боль-
шое
влияние на скорость химических превращений оказывают
такие макроскопические факторы, как перенос вещества, тепла,
238

изменение
размера
и
химического состава поверхности. Раздел
науки,
изучающий (влияние макроскопических факторов
на
ско-
рбеть химических процесов, получил название макрокинетики..
1.
Внешняя диффузионная область.
В
предшествующих
па-
раграфах данной главы была рассмотрена кинетика реакций
в
мономолекулярном хемосорбционном слое катализатора,
когда реакция
не
тормозится диффузионными процессами.
Бы-
ло показано,
что
скорость реакции равна
w
s
=kSc
n
s
,
n>0.
(17.31)
Здесь
cs —
концентрация реагирующего вещества
в
поверх-
ностном
слое, пропорциональная
его
концентрации
у
поверх-
ности
катализатора.
При
протекании химического процесса происходит умень-
шение
исходных веществ
на
поверхности катализатора
и
обра-
зование
продуктов реакции. Пополнение первых
и
удаление
вторых происходит
за
счет
переноса вещества
из
объема газо-
вой
(или жидкой) фазы
и
обратно. Механизм этого переноса
—
обычно диффузионный,
так как
в
отсутствии принудительных
потоков
он
обусловлен наличием градиента концентрации
реа-
гентов
между
объемом
и
поверхностью.
В соответствии
с
уравнениями
для
скорости диффузии
При
установившейся диффузии
dc
Ac
Сл
—
с*»
—=—=--V^-
<
17
-
33
>
dx
Ь о
"W—f-<*-*>.
(17-34)
Здесь
с
0
—
объемная концентрация реагента,
б —
толщина
диффузионного
слоя
у
.поверхности катализатора.
При
внешнедиффузионном торможении
(на
непористых ката-
лизаторах) скорость реакции зависит
от
скорости диффузион-
ного потока реагента
к
«поверхности. Поэтому
для
реакции
первого порядка, когда
w
s
=
kSc
s
,
при
стационарном состоянии получим
»s=«W
и
kSc
s
=-^ {c
o
-c
s
).
(17.35)
Из
этого соотношения находим,
что
c
s
= Ц—
с
0
(17.35а)
239

и
соответственно
Щ=
^g-*.
(17.36)
При
малых значениях отношения
k8/D
получим
w
s
=
kSc
0
,
(17.37)
т.
е. кинетическое уравнение реакции первого порядка относи-
тельно с
0
. При значениях
k8/D>l
находим, что
^i
(17.38)
Ws
c
0
,
т.
е. получаем уравнение переноса типа уравнения
(17.34)
для
случая, когда
cs=0.
Первую предельную область, в которой можно пренебречь
влиянием макрокинетических факторов, называют кинетиче-
ской
областью,
вторую — внешнедиффузионной областью.
Повышение температуры вызывает значительное увеличение
скорости
реакции в кинетической области в соответствии с
уравнением Аррениуса:
k=*conste~
EA/RT
.
(17.39)
В
то же время коэффициент диффузии слабо
(D~T
112
)
зави-
сит
от температуры, в связи с чем температурный коэффици-
ент
скорости процесса во внешнедиффузионной области бли-
зок
к единице.
Если
в кинетической области реакция может иметь различ-
ные порядки, то во внешнедиффузионной области порядок ре-
акции всегда равен единице. Кроме
этого,
во внешнедиффузи-
онной области обычно наблюдается
сильный
разогрев катали-
затора
по отношению к окружающему его газу, достигающий
сотен
градусов. Это и понятно, поскольку механизм теплопере-
дачи в
этих
условиях аналогичен механизму массопередачи. По-
этому,
если затруднен перенос вещества, то затрудняется и
перенос тепла, выделяющегося на катализаторе.
Переход
процесса во внешнедиффузионную область может
произойти при уменьшении линейной скорости потока, повыше-
нии концентрации (для реакций второго и третьего порядков)
и,
особенно,
при повышении температуры.
2.
Внутренняя диффузионная область. Уравнения Зельдови-
ча и Тиле. Большинство промышленных катализаторов являют-
ся
пористыми телами,
причем
/площадь поверхности пор часто
в десятки тысяч раз превышает площадь внешней, геометриче-
ской
поверхности катализатора. Поверхность шор особенно ка-
талитически активна, но доступность ее для реагирующих ве-
ществ неодинакова: чем глубже
внутри
катализатора лежит
данный участок поверхности, тем труднее осуществляется диф-
фузия
к ней веществ! сквозь
пары:
24Q
