Seminario J.M. Molecular and Nano Electronics. Analysis, Design and Simulation
Подождите немного. Документ загружается.


234 M. Tsukada et al.
nature and will be one of the topics discussed in this chapters. When the electron incident
energy is close to a degenerate molecular level, a large loop current is often generated
inside the molecule [5]. The internal current distribution is similar to that induced by
the magnetic field.
According to the principle of the quantum mechanics, since the number of the electrons
in the molecular island and the phase of the wavefunction in a bridge region are a pair
of conjugate physical quantities, there is an uncertainty relation between the two. If the
bottleneck at the connection part is weak, the phase tends to be a good quantum number,
and a coherent quantum transport is expected. If the bottleneck is strong enough, the
electron number in the molecular island will be more or less well defined. In this case
the electron transfer is associated with the energy dissipation to the phonon system
or the electro-magnetic environment. The crucial problem is to know which regime,
coherent or dissipative, dominates the electron transport. Moreover, it is an interesting
problem to know the nature of the transition between the two regimes and to explore
the marginal situation. For the study of this problem, effects of the electron coupling
with medium degrees of freedom should be seriously considered.
2. Non-equilibrium Green’s function with tight-binding bases
In this section, as the basic theoretical approach for the quantum transport, non-
equilibrium Green’s function method is briefly summarized. Hamiltonian H of the
whole system is written as the sum of the Hamiltonian H
0
of the free molecule and its
interaction with the environment ,
H =H
0
+ (1)
The self-energy term takes into account the interaction with electrodes, many-body
effects such as electron–phonon and electron–electron interactions. The retarded and
advanced Green’s functions are defined by
G
R
E =
EI −H
0
−
R
+i
−1
(2)
G
A
E = G
R
E
†
(3)
with a positive infinitesimal . The lesser Green’s function is defined by
G
<
E = G
R
E
<
EG
A
E (4)
which is used to obtain the current between the site i to j,
J
ji
E =
2e
h
Re
H
ji
G
<
ji
E
(5)
In the above, H
ji
is the ji element of the Hamiltonian H
0
. All the effects
due to the interactions with the environment are included in
RA
and the lesser

Quantum electron transport for molecular devices 235
self-energy
<
. When the many-body effect and the electron–phonon coupling are
neglected, the self-energy comes only from the coupling with leads. In this case
<
is
given by
<
E = i
f
E
E (6)
E = i
R
E −
A
E (7)
where f
and
RA
denote the Fermi distribution function in the lead , and the retarded
(advanced) self-energies, respectively. The transmission probability from lead to
is given by
T
E = Tr
G
R
G
A
(8)
The Hamiltonian H
0
can be obtained in a self-consistent manner in the framework of the
DFT with the localized basis set. For the simplest approximation, we use phenomeno-
logical tight-binding model.
3. Effects of the linkage structure on the conductance
of molecular bridges
Here we consider how the terminal structures of the molecules affect the conductance
of the molecular bridge. The transmission spectra of the phenalenyl molecule [6] and
the tape porphyrin molecule [7] are examined as case study. In all the cases, the
electronic states of the whole systems are described by the density functional–derived
self-consistent tight-binding method [8–10], in which the basis is assumed to be the
localized atomic orbitals.
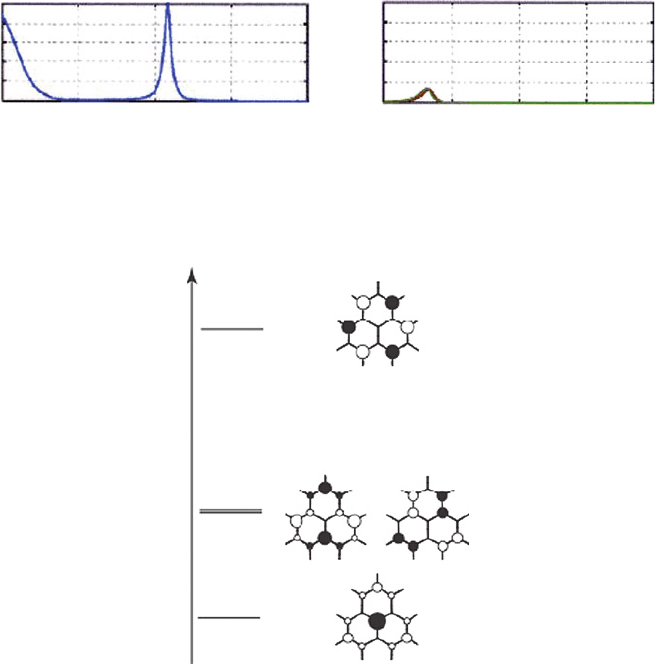
Figure 1 shows the molecular bridge of the phenalenyl molecule attached to the two
gold electrodes through the mercapto-vinyl groups [6]. The difference between the two
systems in (a) and (b) of Figure 1 is seen in the positions of the connecting sites of the
leads (mercapto-vinyl groups), i.e., and sites for the corresponding cases.
The transmission spectrum when both leads are attached to the sites is shown in
Figure 2(a), while for the case with the leads attached to the site it is shown in
Figure 2(b). In both figures, the origin of the electron energy is the Fermi level of the
gold electrodes. For the case with the leads at the sites, the transmission peak appears
(a)
α
β
X
s
s
(b)
X
s
s
Figure 1 Structure of phenalenyl molecular bridge (X==C atom). The mercapto-vinyl groups
are attached to (a) site and (b) site
236 M. Tsukada et al.
–0.1
0.0
1.0
0.0
1.0
–0.5
0.0
0.5 1.0
–0.1 –0.5 0.0 0.5 1.0
(a)
(b)
Figure 2 The transmission spectra for the phenalenyl molecular bridges shown in Figure 1.
Labels (a) and (b) correspond to those of Figure 1
Energy
a
1
″
a
2
″
e″
Figure 3 The energy diagram (schematic) and wave-functions of phenalenyl molecule
at the very vicinity of the Fermi level, but not for the case with the leads at the sites.
In the latter case, the prominent peak at around the Fermi level disappears.
Figure 3 shows the energy diagram of the free phenalenyl molecule. The transmission
peak in the vicinity of the Fermi level is caused by
1
orbital which has no amplitudes
at the sites. This orbital is a single occupied molecular orbital (SOMO) of phenalenyl.
It is easily understood from the nature of the SOMO orbital that the orbital
1
does not
contribute to the transmission, if the leads are connected to sites. This is the reason
for the disappearance of the transmission peak near the Fermi level in Figure 2b. Such
a sensitivity of the conductance on the terminal sites has been also found in the tape-
porphyrin molecules [11]. Tape porphyrin is a sort of the oligomer of the porphyrin,
which shows the vanishing of the HOMO–LUMO gap for a very long chain length. We
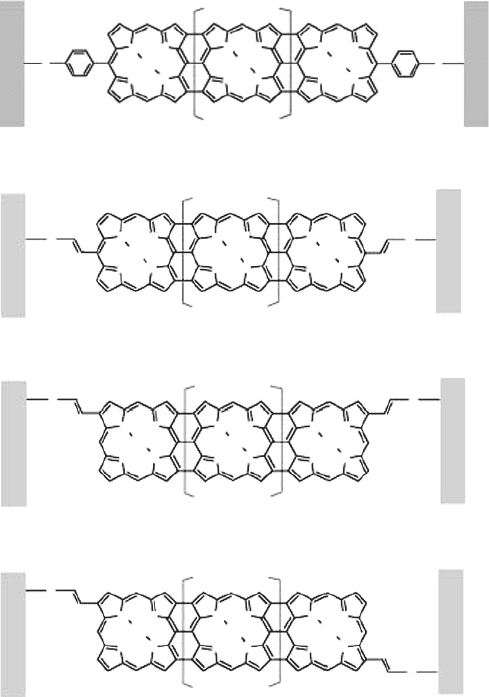
investigated four different linkage structures of the tape-porphyrin to the gold electrodes
as shown in Figure 4. For all the cases, the numbers of the porphyrin molecules in
the chain is assumed to be 8 (n=6). The calculated results of the transmission spectra
Quantum electron transport for molecular devices 237
S
(a)
N
N
N
N
N
N
N
N
N
N
N
S
N
H
H
H
H
H
H
n
S
(b)
N
N
N
N
H
H
N
N
N
N
H
H
N
N
N
S
N
H
H
n
S
N
N
N
N
H
H
N
N
N
N
H
H
N
N
N
N
S
H
H
(c)
n
S
(d)
N
N
N
N
H
H
N
N
N
N
H
H
N
N
N
N
H
H
S
n
Figure 4 Four kinds of bridge structures using a tape porphyrin
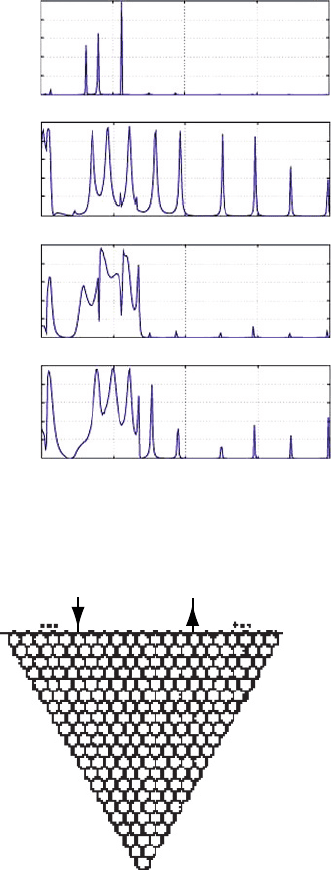
are shown in Figure 5. It is remarkable that only a small difference of the linkage
part dramatically influences the conductance of the molecular bridge. Namely, among
the four bridges from A through D shown in Figure 4, the case B shows the largest
conductance, because there is a prominent transmission peak very close to the electrode
Fermi level.
These findings indicate that for designing a whole system of the molecular bridge,
special attention should be paid to the linkage parts of the molecule to the electrodes.
4. Internal large loop currents
Figure 6 illustrates a triangular nano-graphene sheet bound with zigzag edges. The
protruded atoms along the topmost zigzag edge are numbered from 1 to N . The number
of atoms in the nano-graphene is N
2
+4N +1. The smallest molecule with N = 2
238 M. Tsukada et al.
G(E
)/G
0
(a)
(b)
(c)
(d)
1.0
0.0
0.05
0.00
1.0
0.0
Energy (eV)
–1.0 –0.5 0.5 1.0
1.0
–0.0
0.0
Figure 5 Transmission spectra for the corresponding molecular bridges shown in Figure 4
12 s d N
Figure 6 A structure of triangular nano-graphene
corresponds to the phenalenyl molecule discussed in the previous section, but here we
focus on the larger system with N =56. The source s and the drain d are connected to
the top edge at s d =N /4 +1 3N/4. The connection would be made by the vinyl
group. As for the lead-molecule coupling, we set t
=06t.
The isolated nano-graphene molecule has many doubly degenerate energy levels in
the vicinity of the Fermi level [12], although there are N −1-fold degenerate levels at
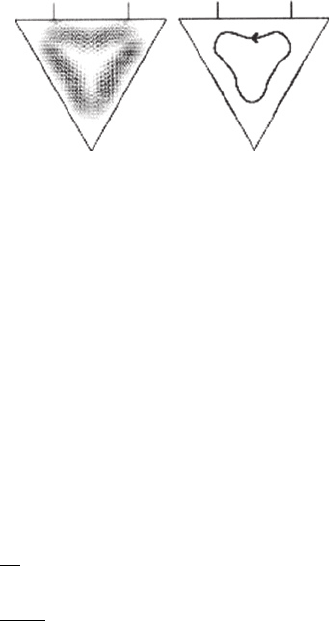
Quantum electron transport for molecular devices 239
(a)
(b)
Figure 7 (a) Microscopic loop current distribution in the trianglar nano-graphene and
(b) a schematic view of its current direction
E = 0, which correspond to the edge states. Due to the localized character of the edge
state, they do not contribute to the resonant current [12]. Figure 7(a) shows the internal
bond current J
ij
(E) (from site i to j) at one of the degenerate levels E =−0165t, so that
the strongest one is expressed by the darkest color. Figure 7(b) schematically illustrates
the orientation of the current flow. Noticeably, a large current loop appears circulating a
large area of the graphene molecule. The strength of the current is much larger than the
source–drain current. Even when the source and the drain sites are moved to different
sites along the upper edge, almost the same current patterns are obtained [12]. The
internal current distribution is determined from the nature of the particular degenerate
molecular orbitals, rather than being accidentally induced by the current from the leads.
The distribution of the internal bond current is analyzed as follows. The current
flowing through the bond connecting the sites i and j is given by
j
ij
=
4e
h
Im
∗
i
H
ij
j
=
4eH
ij
h
v
i
vj
−
vi
j
a
a
v
sin
−
v
(9)
where label the molecular states,
a
a
v
are their amplitudes, and
v
are the
phases of the coefficients expanding the whole scattering electron wave with the energy
E. On the other hand
i
i=1 2
are the LCAO coefficients of the particular molecular
orbital in the isolated molecule. The envelop factor of
a
a
sin
−
does not
depend on the atomic site in the molecule, and resonantly enhanced when the electron
energy becomes closer to a degenerate molecular level. In this case, the states and
are certain components of the degenerate state. Because of the sine function factor of
the phase difference
−
, the energy corresponding to the maximum of the envelop
factor is slightly higher or lower than the just on resonance energy. Because of the
resonantly enhancing feature of the envelop factor, the magnitude of the loop current
becomes larger than the source–drain current often by several tens of times.
The factor
i
j
−
i
j
in Eq. (9) expresses the microscopic current distribu-
tion inside the molecule. Interestingly enough, the same factor appears for the current
distribution of the isolated molecule under a static magnetic field. Such current causes
the diamagnetism of the molecule in general, and for a mesoscopic system, it is the
current distribution of the magnetically induced persistent current. One might speculate
a close relationship between the source–drain induced loop current and the magnetic
field–induced molecular current.
240 M. Tsukada et al.
5. Effect of electron–phonon coupling
Though the conductance value of molecular bridges so far theoretically predicted has not
been so much reduced from the quantization value G
0
(= 1/129k, experimentally
reported values have been usually by some orders of magnitude smaller than this.
Unfortunately there have been few conductance measurements, where the contact is
characterized in the atomic level. On the theoretical side, approaches ignoring the
electron–vibration coupling may not be always satisfactory. Such approaches might
result in too much enhancement of the coherent nature and tends to estimate larger
values for the conductance. To clarify the reason for the gap between the theory and
experiment, we should look into the effect of the molecular vibration on the electron
transfer processes.
With the decrease of the transfer integral in the molecular region, the electronic
states would change from the extended states to the localized states due to the polaron
formation. By considering the transition between these polaron-like states, the carrier
transfer in the molecular bridges can be properly analyzed. In this section we propose a
unified method to treat the extended and the polaron-like localized states coupled with
the molecular vibrations. Second, we will clarify the electron transport processes based
on the transition rates between the coupled electronic states with the vibration modes.
The case study is made for the one-dimensional molecular bridge made of the thiophene
molecules [13].
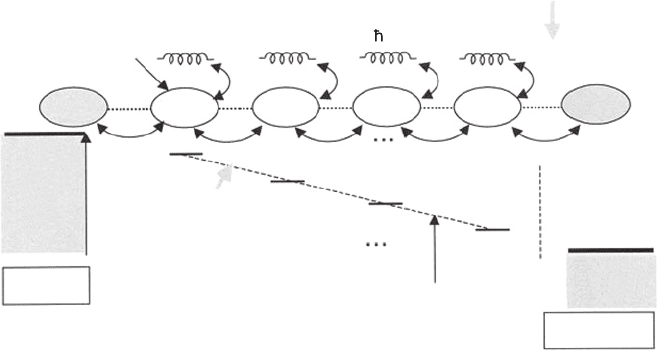
The model we treat in this chapter is shown in Figure 8. It consists of molecules
arranged in a chain in the bridge region and two outer electrodes. The molecules should
be regarded to form a large single molecule for the stronger interaction. We consider
the case in which one additional electron or hole exists over the otherwise neutral whole
molecules. Only a single state, i.e. LUMO for the case of electron or HOMO for the
case of hole, is considered as the electronic state on each molecule (or molecular unit
for the stronger interaction case).
HOMO
(or LUMO)
Electron–vibration
coupling
V
B1
V
V
V
V
B2
E
1
E
0
E
2
E
N
E
N+1
Site: N
Site: n
= 1
Site: n
= N + 1
Site: n
= 0
n = 2
Transfer integral
Electric field
Electrode
Electrode
γ
λ
(n)
ω
λ
Figure 8 A model of the bridge of linearly arranged thiophene molecules

Quantum electron transport for molecular devices 241
The Hamiltonian of the total system is given as
H
total
=H
MB
+H
E
+H
MB−E
(10)
where the first two terms of the right hand side describe molecule(s) and electrodes,
respectively, and the last term is their coupling term. Each term on the right hand side
of the above equation is written as
H
MB
=
N
n=1
E
n
a
+
n
a
n
+
N −1
n=1
Va
+
n
a
+
n+1
a
+
n+1
a
n
+
h
b
+
b
+
N
n=1
n
h
a
+
n
a
n
b
+
+ b
(11a)
H
E
=E
0
a
+
0
a
0
+E
N +1
a
+
N +1
a
N +1
(11b)
H
MB−E
=V
B1
a
+
0
a
1
+a
+
1
a
0
+V
B2
a
+
N
a
N +1
+a
+
N +1
a
N
(11c)
Here a
+
n
a
n
creates (annihilates) an electron or hole in the n-th molecule (hereafter,
“molecule” should be interpreted as a molecular unit for a strong V case) or one of the
electrodes with energy E
n
.
The indexes n =0 and n =N +1 correspond to the electronic state of the electrodes.
Since the number of carriers is assumed to one,
N +1
n=0
a
+
n
a
n
=1·b
+
b
creates (annihilates)
a vibration quanta in the mode with energy
. The electron–vibration coupling
between the carrier at the n-th molecular site and -th vibration mode is given by the
parameter
n
.
For the estimation of the electron–phonon coupling parameter, the following relation
is useful;
n
=−
m
2h
d ·e
(12)
with
d being the 3N
atom
-dimensional relaxation vector from neutral state to ionic state
(N
atom
is the number of atoms in the molecule), and e
being the -th normal vibration
mode of the molecule. In the case of the thiophene molecule, among 21 normal vibration
modes, the 16th mode from the lowest has the largest coupling. This is because the
displacement of the 16th mode is nearly the same as the relaxation vector. Thus the
value of the coupling constant is calculated by ab initio molecular orbital method.
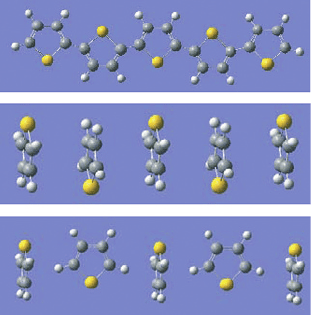
Transfer integral V is also estimated by ab initio molecular orbital method. Examples
of the transfer integral of the HOMOs of thiophene molecules are shown in Figure 9.
The electronic states in the molecular bridge region can be obtained as follows. First,
in the limiting case of V =0, the exact wavefunctions are given by
m
n
=
exp−
n
b
+
−b
m
n
(13)
242 M. Tsukada et al.
|V | = 2.1 eV
|V
| = 0.7 eV
|V
| = 0.0 eV
Figure 9 Values of transfer integral for the linear array of thoiphene molecules
which will be called “the polaron-like states”, hereafter. Here “
m
” means the vibration
state with m
quanta in the mode . Second, if the electron–vibration coupling is equal
to 0, the eigen states should be in the form of
m
m
=
N
n=1
f
m
n
n
m
(14)
which are called the “the undressed states”. The first factor of
N
n=1
f
m
n
n
corresponds
to the molecular orbital for the system without vibration degrees of freedom. The state
m
means
m
1
m
2
···
m
n
···. Generally, the wavefunction is expressed by
m
a
a
=
N
n=1
A
a
n
m
a
n
+
N
m=1
B
a
m
m
a
m
(15)
with A
a
n
and B
a
m
determined by the minimum energy condition for the ground states:
0
a
=
N
n=1
A
a
n
0
n
+
N
m=1
B
a
m
0
m
=
N
n=1
A
a
n
exp−
n
b
+
−b
+C
a
n
n
0
ph
(16)
Here we set C
a
n
=
N
m=1
f
m
n
B
a
m
.
The electronic states in the molecular bridges with five sites will be shown below.
In this model the energy difference between neighboring sites is set to 0.04 eV (see
Figure 8). The single vibration mode is assumed for each molecular units, with the
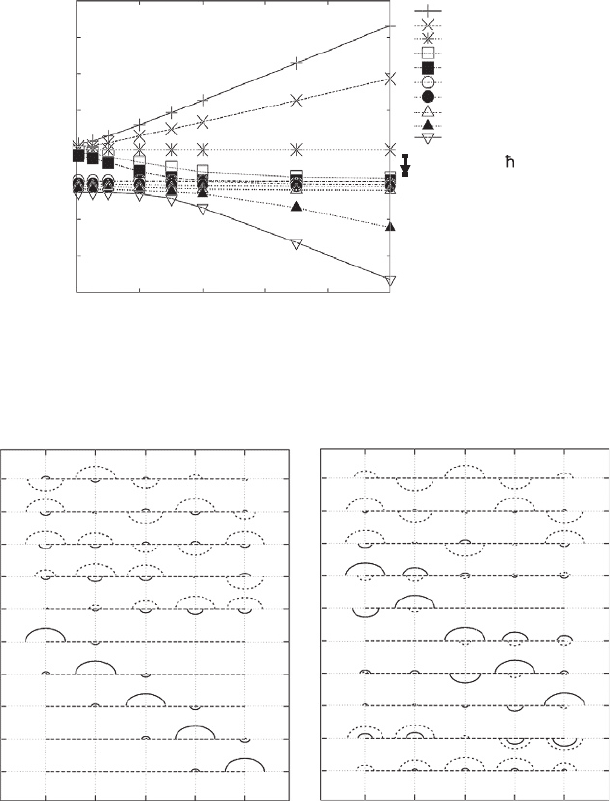
value of the coupling being 1.6. Figure 10 shows how the energy levels of the electronic
states depend on the transfer integral. There are two kinds of states in this figure: one
with almost constant energies and the other showing the linear dependence with transfer
integral.
In Figure 11 the coefficients of the wavefunction are shown in the case of (a) V=
0.1 eV and (b) V=0.7 eV. The coefficients of the polaron-like part and the undressed
Quantum electron transport for molecular devices 243
#10
#9
#8
#7
#6
#5
#4
#3
#2
#1
2
1.5
1
0.5
–0.5
–1
–1.5
–2
0 0.2 0.4 0.6 0.8 1
0
Energy (eV)
ΔE
p
= γ
2
hω
=
0.46 eV
|V| (eV)
Figure 10 Energy levels of the molecular bridges as the function of the transfer integral V. The
parameters are so chosen to satisfy,
2
= 046 eV
10
9
8
7
6
5
5
4
4
3
3
2
1
2
1
54321
State
Site
Site
Figure 11 Composition of each eigen-state coupled with vibration modes for (a)
V
= 01eV
and (b)
V
=07eV. Other parameters are = 018 eV and =16
part are plotted by full and dotted lines, respectively, with the upper and lower half circles
indicating positive and negative values, and the radius being the relative magnitude
normalized by the maximum value. In case (a), the lower and upper five states are the
polaron and the undressed states, respectively. On the other hand, in case (b), from
the third to the seventh, the states are the polaron states, while the other states are the
undressed ones. The ground state for lower V is polaron, but with the increase of V,
the ground state becomes undressed state.
