Seminario J.M. Molecular and Nano Electronics. Analysis, Design and Simulation
Подождите немного. Документ загружается.


4 Luis A. Agapito and Jorge M. Seminario
Table 1 Contraction coefficients and Gaussian exponents for the
inner 1s atomic orbital of the carbon atom (Eq. 3) corresponding
to the 6-31G(d) basis set
u Contraction coefficients Gaussian exponents
d
u
u
1 0.001834700 3047.52490
2 0.014037300 457.369510
3 0.068842600 103.948690
4 0.232184400 29.2101550
5 0.467941300 9.28666300
6 0.362312000 3.16392700
where i and j count over all electrons and b counts over all nuclei, and Z
b
is the atomic
number of the atom b. If the system contains n electrons then the wavefunction of
the molecular system is a function of 3n spatial coordinates and n spin coordinates.
Therefore, calculating the complete electronic wavefunction is computationally chal-
lenging simply because the wavefunction is a mathematical function that contains more
information of the system than needed for specific applications.
The first Hohenberg–Kohn theorem [22] established that all the properties of a molec-
ular system in the ground state are determined by the ground-state electron density
0
x y z, which is a function of only three variables. This theorem circumvents the
use of the wavefunction; instead, the electron density function is used to calculate the
properties of a molecular system. This theorem together with the constrain search of
Levy [23] finally sets DFT on a formal basis.
In 1965 Kohn and Sham [24] published a method to determine the electron density
without having to find the real wavefunction. They demonstrated that the electron
density of a molecular system of interacting electrons can be represented with the
electron density of an ideal or ficticious system of non-interactive electrons subjected
to an effective potential
s
. Therefore, the interacting many-electron problem is split
into several non-interacting one-electron problems, which are governed by the following
one-electron Kohn–Sham (KS) equations:
ˆ
h
KS
r
KS
i
r =
KS
i
KS
i
r (6)
where the one-electron KS Hamiltonian
ˆ
h
KS
is defined as:
ˆ
h
KS
r =−
1
2
2
r
+
s
r (7)
and the external potential for the fictitious electrons is defined as:
s
r =−
b
Z
b
r −r
b
+
r
r −r
dr
+
xc
r (8)
where
xc
is the exchange-correlation potential
xc
r ≡
E
xc
r
r
(9)
Metal–molecule–semiconductor junctions 5
The external potential v
s
is found by solving Eq. (6) self-consistently. The KS molec-
ular orbitals (
KS
i
), shown in Eq. (6), are expanded in terms of the GTOs defined in
Eq. (2).
KS
i
=
B
r=1
c
ri
r
(10)
where B is the number of basis functions of the molecular system. By inserting Eq. (10)
in Eq. (6) and applying the variational principle, a Roothaan-type matrix equation is
obtained. For example, the matrix equation for a molecular system that has only five
basis functions is
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
h
KS
11
h
KS
12
h
KS
13
h
KS
14
h
KS
15
h
KS
21
h
KS
22
h
KS
23
h
KS
24
h
KS
25
h
KS
31
h
KS
32
h
KS
33
h
KS
34
h
KS
35
h
KS
41
h
KS
42
h
KS
43
h
KS
44
h
KS
45
h
KS
51
h
KS
52
h
KS
53
h
KS
54
h
KS
55
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
C =
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
S
11
S
12
S
13
S
14
S
15
S
21
S
22
S
23
S
24
S
25
S
31
S
32
S
33
S
34
S
35
S
41
S
42
S
43
S
44
S
45
S
51
S
52
S
53
S
54
S
55
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
E
KS
C (11)
where h
KS
rs
are matrix elements of the one-electron KS Hamiltonian operator
ˆ
h
KS
. These
matrix elements are defined as:
h
KS
rs
=
r
ˆ
h
KS
s
(12)
The overlap integral S
jk
between two basis functions is:
S
jk
=
j
k
(13)
C is a matrix composed of the expansion coefficients c
ri
, which are defined in Eq. (10).
E
KS
is a diagonal matrix composed of all the eigenvalues (energies) of the one-electron
KS equation defined in Eq. (6).
E
KS
=
⎛
⎜
⎜
⎜
⎜
⎜
⎝
KS
1
0000
0
KS
2
000
00
KS
3
00
000
KS
4
0
0000
KS
5
⎞
⎟
⎟
⎟
⎟
⎟
⎠
(14)
The expansion coefficients, c
ri
, of the molecular orbitals are found by solving itera-
tively Eq. (11) [25].
=
n
i=1
KS
i
2
(15)
At all steps of the iteration, the expansion coefficients are updated. Consequently, new
KS molecular orbitals, Eq. (10), and electron densities, Eq. (15), are obtained during the
iterative process. When self-consistency is reached, the ground-state electron density
and KS molecular orbitals can be evaluated. All properties for the molecular system can
be extracted from the ground-state density, according to the Hohenberg–Kohn theorem.

6 Luis A. Agapito and Jorge M. Seminario
2.1.3. Molecular electrostatic potential
A molecular system can be modeled as an electronic device, encapsulating all the
chemistry of the system behind the electron density . The equivalent electrostatic
potential for such electronic device, measured at a point of space r = x y z, can
be calculated as:
x y x =
Z
r −R
−
x
y
z
r −r
dx
dy
dz
(16)
where the electron density is defined in Eq. (15).
2.2. Electronic properties of crystalline materials
In the case of finite systems, atomic orbitals, Eq. (2), are used to build up the molecular
orbitals. For infinite systems, Bloch functions
r
k, are used to build up crystalline
orbitals
i
r
k:
i
r
k =
c
i
k
r
k (17)
where r and
k represent vectors in the direct and reciprocal space, respectively. Bloch
functions are defined as follows
r
k =
T
r −
A
−
Te
i
k
T
(18)
where
T represents all direct lattice vectors.
represents contracted GTOs as defined
in Eq. (2). The subscript counts over all the basis functions used to expand the unit
cell,
A
indicates the coordinates of the atom on which
is centered. The Bloch
functions Eq. (18) are constructed to satisfy the Bloch theorem:
r +
T
k =
r
ke
i
k
T
(19)
Bloch functions with different wavevectors, k, do not interact each other; therefore,
a periodic system can be solved independently for each value of k.
A crystalline orbital Eq. (17) resembles the definition of an MO Eq. (10) in finite
systems. The expansion coefficients for the crystalline orbitals c
i
, Eq. (17), are found
analogously to the case of finite systems. The matrix Ck, which contains the coeffi-
cients c
i
, is found by solving self-consistently Eq. (20) for each k point.
H
KS
kCk = SkCkEk (20)
where H
KS
k is the Kohn–Sham Hamiltonian matrix in reciprocal space
H
KS
k =
r
k
ˆ
h
KS
r
k
=
T
r −
A
−
0
ˆ
h
KS
r −
A
−
T
e
i
k
T
Metal–molecule–semiconductor junctions 7
Sk is the overlap matrix over the Bloch functions
S
k =
r
k
r
k
=
T
r −
A
−
0
r −
A
−
T
e
i
k
T
EK is a diagonal matrix that contains the eigenvalues
k
i
for a given point k. The
number of eigenvalues per k point is equal to the number of basis functions of the unit
cell, and Ck contains column-wise the coefficients of the crystalline orbitals.
The density of states (DOS) of the infinite system is found according to
DOS = 2
ik
−
k
i
=
2
V
BZ
i
BZ
−
k
i
d
3
k (21)
where V
BZ
is the volume of the first Brillouin zone. The software Crystal 03 [26] is used
to calculated the DOS for the different crystalline materials that are used throughout
this work.
2.2.1. DOS of Au and Pd crystals
The Au and the Pd crystals are modeled as FCC lattices with space group number
225. The lattice parameters for the conventional cells are a = 4078 Å for gold and
a =3891 Å for palladium (Figures 1 and 2). The primitive cell for both crystals contains
one atom and is defined by the following primitive vectors
A
1
=
1
2
aˆy +
1
2
aˆz
A
2
=
1
2
aˆx +
1
2
aˆz
–15 –10 –5 0 5
0
0.5
1
1.5
2
2.5
3
3.5
Energy (eV)
DOS (states eV
–1
atom
–1
)
s
p
d(t
2g
)
d(e
g
)
total
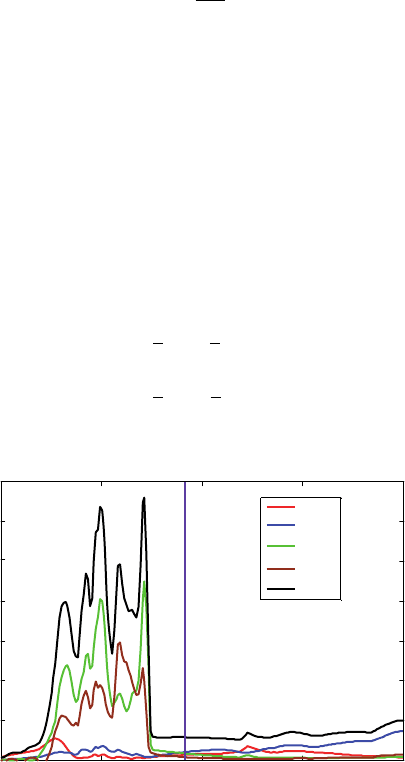
Figure 1 DOS for the Au crystal. Fermi level is at −583 eV using the B3PW91 functional with
the LANL2DZ basis set and ECP

8 Luis A. Agapito and Jorge M. Seminario
–15 –10 –5 0 5
0
0.5
1
1.5
2
2.5
3
3.5
Energy (eV)
DOS
(states
eV
–1
atom
–1
)
s
p
total
d(t
2g
)
d(e
g
)
Figure 2 DOS for the Pd crystal obtained using the B3PW91 functional and LANL2DZ basis
set and ECP. The Fermi level is at −559 eV
and
A
3
=
1
2
aˆx +
1
2
aˆy
The calculation of the electronic structure is performed at the B3PW91 level of
theory combined with the LANL2DZ basis set. The total DOS for gold (black curve) is
reported in Figure 1. We also compute the contribution of each type of basis function
(s-, p-, or d-type) to the total DOS. For consideration to the symmetry of the d-type
functions, their contribution is split into two groups: the contribution of the d
xz
d
yz
d
xy
basis functions, which present t
2g
symmetry and the contribution of the d
z
2
∗
,d
x
2
−y
2
basis
functions, which present e
g
symmetry. For Au and Pd, most of the electrons available
for conduction (at their Fermi level) have a d-character.
2.2.2. DOS of silicon crystal
Silicon presents a crystal structure of the diamond (point group number 227). The
conventional cell has a lattice parameter a = 542 Å. The primitive cell is defined by
the following primitive vectors
A
1
=
1
2
aˆy +
1
2
aˆz
A
2
=
1
2
aˆx +
1
2
aˆz
and
A
3
=
1
2
aˆx +
1
2
aˆy
∗
The orbital d
z
2
is more properly referred as d
2z
2
−x
2
−y
2
.
Metal–molecule–semiconductor junctions 9
with two atoms per each primitive cell, the basis vectors for these atoms are
B
1
=−
1
8
A
1
−
1
8
A
2
−
1
8
A
3
=−
1
8
aˆx −
1
8
aˆy −
1
8
aˆz
B
2
=+
1
8
A
1
+
1
8
A
2
+
1
8
A
3
=+
1
8
aˆx +
1
8
aˆy +
1
8
aˆz
The crystal is calculated using the B3PW91 level of theory. Two sets of calculations,
using different basis sets, are carried out.
The full-electron 6-31G(d) basis set uses four s-type, nine P-type, and six d-type
Gaussian functions to represent the electrons of a and Si atom. The total DOS and the
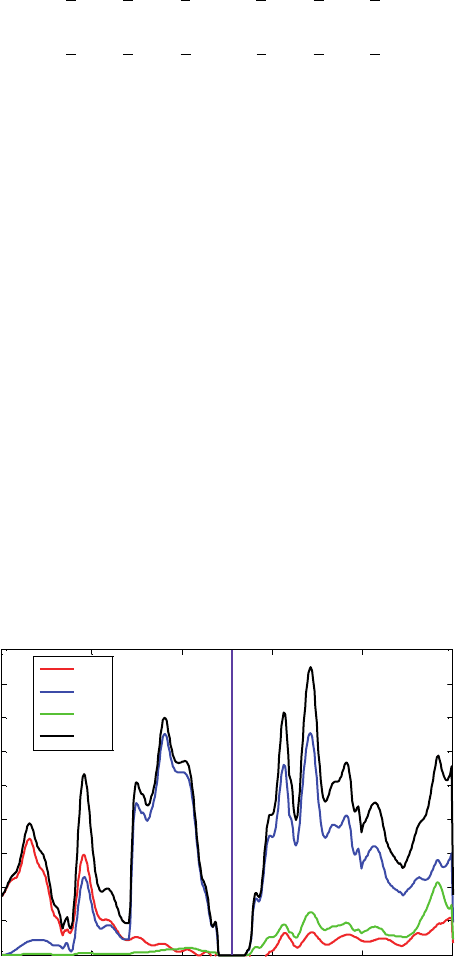
s, p, and d projections obtained using that basis set are shown in Figure 3. The states
around the Fermi level have mostly a p-character and a bandgap of 0.72 eV; the midgap
is at −222 eV.
The LANL2DZ basis set supports elements with large atomic numbers, such as gold.
Whenever the molecule under study contains gold atoms, the system is calculated using
the LANL2DZ basis set. Therefore, for compatibility purposes, the DOS of Si using
the LANL2DZ basis set is also obtained. LANL2DZ is not a full-electron basis set for
Si; only the four valence electrons are considered in the calculations; the remaining ten
core-electrons are modeled by an effective core potential (ECP). The Si DOS using this
basis set is reported in Figure 4; notice that there is not d projection of the total DOS
since no d-type polarization functions are used for Si in the LANL2DZ basis set.
2.2.3. DOS of the (4, 4) CNT
Single-walled carbon nanotubes SWCNTs are one-dimensional crystals with interest-
ing mechanical and electrical properties (See for instance [27]). The geometry and
–15 –10 –5 0 5 10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Energy (eV)
DOS (states eV
–1
atom
–1
)
s
p
d
total
Figure 3 DOS for a silicon crystal calculated using the B3PW91 method and the 6-31G(d)
basis set
10 Luis A. Agapito and Jorge M. Seminario
–10 –5 0 5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Energy (eV)
s
p
total
DOS (states eV
–1
atom
–1
)
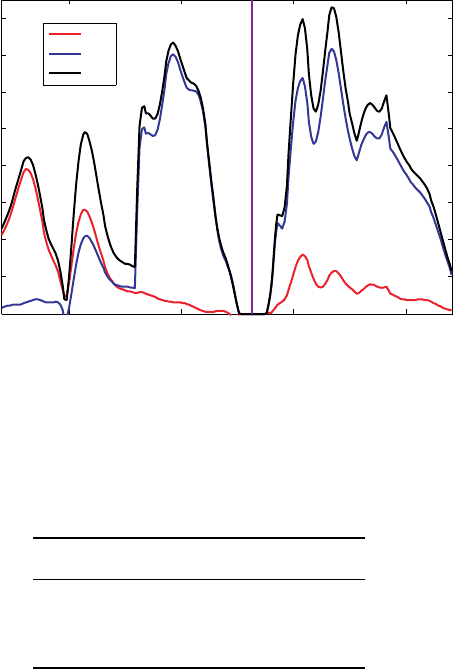
Figure 4 DOS for a silicon crystal calculated using the B3PW91 DFT method and the LANL2DZ
basis set. The Fermi level for the material (purple line) is at −185 eV. The calculated bandgap is
1.11 eV
the electrical behavior of an SWCNT are defined by a pair of integers (m n). It is
known [28] that
Condition Type Bandgap
n −m =3q Semimetallic ∼meV
n −m =3q Metallic 0 eV
n −m =3q Semiconductor 0.5–1 eV
where q is a non-zero integer. Recent breakthroughs in synthetic chemistry [29] have
opened the possibility of using metallic CNTs as contacts to organic molecules. We use
the (4, 4) CNT, which is a metal according to the above table, to explore the electrical
characteristics of CNT–nitroOPE–CNT molecular junctions. The DOS of the (4, 4)
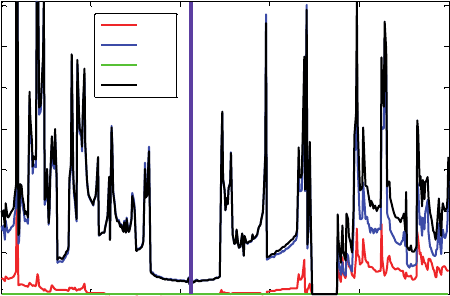
CNT, Figure 5, is calculated using the B3PW91 DFT functional and the 6-31G basis
set. Despite the presence of a gap in the CNT DOS at ∼350 eV, the absence of gaps
at the Fermi level confirms the metallic character of this material. The calculated DOS
is in agreement with previous experimental [30, 31] and theoretical [32–35] findings.
A unit cell of the (4, 4) CNT is modeled by 16 carbon atoms.
2.3. Combined DFT-GF approach to calculate the DOS of a molecule
adsorbed on macroscopic contacts
An isolated molecule has discrete electronic states, which are precisely calculated from
the Schrödinger equation. When the molecule is attached to macroscopic contacts, the
continuous electronic states of the contacts modify the electronic properties of the
molecule. A technique that combines the Density Functional Theory and the Green
Metal–molecule–semiconductor junctions 11
–15 –10 –5 0 5 10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Energy (eV)
s
p
d
total
DOS (states eV
–1
atom
–1
)
Figure 5 DOS for the metallic (4, 4) CNT, which is calculated using the B3PW91/6-31G method
and basis set. The Fermi level (purple vertical line) is at −439 eV
function (DFT-GF) [36, 37] is used to account for the effect of the contacts on the
electronic states of adsorbed molecule.
In a real system, molecules are chemically attached to real contacts, made of atoms,
and not to ideal surfaces. Therefore, information about the interface, obtained at the
molecular level, needs to be provided. This is accomplished through coupling matrices
obtained from quantum-mechanical calculations of the extended molecule (i.e., the
molecule attached to a few atoms from the contacts). The Gaussian 03 [21] software is
used for the quantum-mechanical calculations of all the finite systems throughout this
work. Thus, our calculations consider explicitly the chemistry of the attachment of the
molecule to the contacts instead of unrealistic simulations of a molecule attached to
perfect or ideal surfaces.
For a hypothetical molecular system that has only five basis functions (), the elements
of the Kohn–Sham Hamiltonian matrix (H
KS
) are given by
H
KS
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
1
ˆ
h
KS
1
1
ˆ
h
KS
2
1
ˆ
h
KS
3
1
ˆ
h
KS
4
1
ˆ
h
KS
5
2
ˆ
h
KS
1
2
ˆ
h
KS
2
2
ˆ
h
KS
3
2
ˆ
h
KS
4
2
ˆ
h
KS
5
3
ˆ
h
KS
1
3
ˆ
h
KS
2
3
ˆ
h
KS
3
3
ˆ
h
KS
4
3
ˆ
h
KS
5
4
ˆ
h
KS
1
4
ˆ
h
KS
2
4
ˆ
h
KS
3
4
ˆ
h
KS
4
4
ˆ
h
KS
5
5
ˆ
h
KS
1
5
ˆ
h
KS
2
5
ˆ
h
KS
3
5
ˆ
h
KS
4
5
ˆ
h
KS
5
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
(22)
The atoms of the molecular system can be classified as belonging to the contact 1, the
contact 2, or the molecule (M). For illustration, the atoms conforming the contact 1, the
contact 2, and the molecule are modeled by the
2
3
4
; and
1
5
basis functions,
respectively. After reordering and partitioning H
KS
into submatrices we have:
H
11
=
2
ˆ
h
KS
2
(23)
H
22
=
3
ˆ
h
KS
3
3
ˆ
h
KS
4
4
ˆ
h
KS
3
4
ˆ
h
KS
4
(24)
12 Luis A. Agapito and Jorge M. Seminario
H
MM
=
1
ˆ
h
KS
1
1
ˆ
h
KS
5
5
ˆ
h
KS
1
5
ˆ
h
KS
5
(25)
H
1M
=
2
ˆ
h
KS
1
2
ˆ
h
KS
5
(26)
H
M1
=
1
ˆ
h
KS
2
5
ˆ
h
KS
2
(27)
H
2M
=
3
ˆ
h
KS
1
3
ˆ
h
KS
5
4
ˆ
h
KS
1
4
ˆ
h
KS
5
(28)
H
M2
=
1
ˆ
h
KS
3
1
ˆ
h
KS
4
5
ˆ
h
KS
3
5
ˆ
h
KS
4
(29)
where H
MM
is the submatrix representing the isolated molecule (restricted molecule).
The other submatrix represents the couplings between the molecule (subscript M) and
the atoms of the contact (subscripts 1 and 2).
Then, we create an ordered Hamiltonian matrix (H) and the respective overlap matrix
(S) in the following way:
H =
⎛
⎜
⎝
H
11
H
1M
H
12
H
M1
H
MM
H
M2
H
21
H
2M
H
22
⎞
⎟
⎠
S =
⎛
⎜
⎝
S
11
S
1M
S
12
S
M1
S
MM
S
M2
S
21
S
2M
S
22
⎞
⎟
⎠
(30)
This Hamiltonian matrix for the extended molecule (H) is also recalculated as the bias
electrical field is applied to the junction in order to account for the reorganization
of the molecular electronic structure due to the presence of such field. This allows
us to study among others the effects of the external bias potential on charge transfer
between the molecule and the contacts, the shift of molecular levels and the shape
changes of the molecular orbitals, which have a direct effect on the conductance of
the junction. These effects are needed to explain the nonlocal behavior of molecular
systems presenting highly nonlinear features such as rectification, negative differential
resistance, memory hysteresis, etc. Notice that the molecule itself does not have an
integer charge in any of the charge states of the extended molecule because the charge
distributes between the isolated molecule and the metal atoms. Charge transfers between
the molecule and contact occur even at zero bias voltage and also as a result of an
externally applied field. Certainly, this charge transfer is determined by the metal atoms
attached to the molecule; these metal atoms together with the continuum define specific
tip. It is clearly demonstrated from theoretical as well as experimental information
[3, 14, 38] that the connection of the molecule to the metal is only through one or
two metal atoms as concluded in [3]. However, the effect of local interactions with the
atoms located beyond these nearest neighbors on the actual molecule is very small and

Metal–molecule–semiconductor junctions 13
usually truncated; this constitutes the strongest approximation of our procedure only if
the molecule were realistically connected directly to a continuum. Fortunately, there is
strong evidence that it is an acceptable approximation because it precisely considers
the chemistry and physics of the actual local attachment or bonding of the molecule to
the surface atoms [3, 14]. Methods such as the so-called “non-equilibrium” for instance
are shown to include only the Hartree response of the system, thus missing important
physics of the problem [39].
The coupling between atoms of the contact and those of the molecule yields the
self-energy term,
j
:
j
=H
Mj
g
j
H
jM
j = 1 2 (31)
which depends on the complex Green function, g
j
, describing the contact j. The complex
g
i
can be obtained from any source as long as it can be represented in matrix form of
the appropriate dimensions; it provides the information from the contact to the DFT-GF
formalism. We choose to generate the Green function for the conctacts using Crystal 03
since it allows obtaining a high-level electronic structure of a bulk system of any shape
using DFT. This complex function is defined as:
g
j
E =−
√
−1
⎛
⎜
⎜
⎝
g
1
j
0
0 ··· g
n
j
j
⎞
⎟
⎟
⎠
j = 1 2 (32)
where each value of the diagonal matrix is proportional to the local density of states
DOS, which has been calculated in Section 2.2.
g
k
j
E =
⎛
⎜
⎜
⎜
⎝
DOS
j
s
k
E 000
0 DOS
j
p
k
E 00
0 0 DOS
j
d
k
t
2
g
E 0
0 0 0 DOS
j
d
k
e
g
E
⎞
⎟
⎟
⎟
⎠
(33)
In order to keep consistency in the matrix dimensions of Eq. (32), the index k runs
over all the interfacial atoms that represent contact jk =l n
j
. Each diagonal term
of Eq. (33) is again another diagonal matrix, in such a way that the size of DOS
j
s
k
E
is equal to the number of s-type basis functions used to model the electronic structure
of the type of atom that composes contact j.
The coupling of the molecule to the contacts is obtained from molecular calculations
(H
iM
and H
Mi
shown in Eq. (30)) that consider the atomistic nature of the contact–
molecule interface. The interaction terms defined in Eq. (31) are added to the molecular
Hamiltonian to account for the effect of the contact on the molecule:
H
e
=
⎛
⎜
⎝
H
11
H
1M
H
12
H
M1
H
MM
+
1
+
2
H
M2
H
21
H
2M
H
22
⎞
⎟
⎠
(34)
