Seminario J.M. Molecular and Nano Electronics. Analysis, Design and Simulation

Подождите немного. Документ загружается.

64 Ying Luo et al.

Ground-state

Excited-state

shift

(A)

(B)

Phonon Absorption Spectrum

cis -2-Butene

trans-2-Butene

Normalized Intensity

cis - Same side of the double bond

trans - Opposite sides of the double bond

Wavenumber (cm

–1

)

0 500 1000 1500 2000

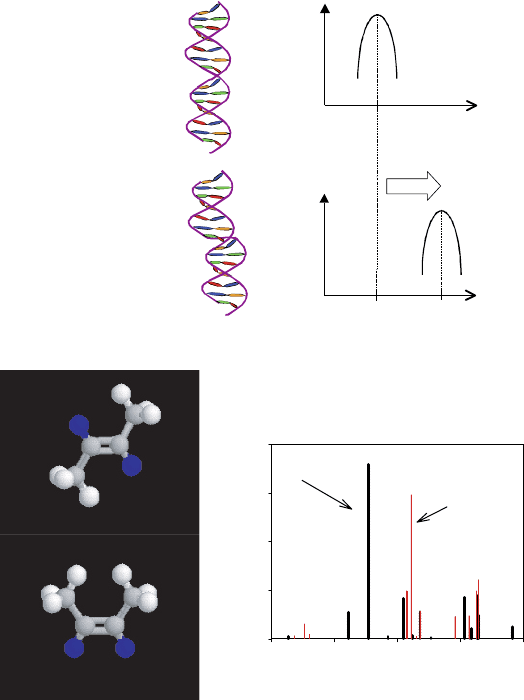
Figure 5 Basic ETO effect: (A) hypothetical DNA example, (B) isomers of butane and simulated

spectra [1]

2.2.1. Simulation and analysis of butene isomers

In the initial study, the cis-trans isomers of butene have been chosen because they

are very well known and simple examples of a ground- and metastable-state pair with

significantly different geometries. The cis-trans isomers are geometric isomers, a type

of stereoisomerism in which atoms or groups display orientation differences around a

double bond, such as trans-2- and cis-2-butene as was shown earlier in Figure 5(B). This

work demonstrated molecular isomers that yield different sets of vibrational frequencies.

In this case to be studied, photo-induced transitions bring about the conversion from

one geometric shape (i.e., trans-2-butene) to another (i.e., cis-2-butene) through rotation

about a double bond and the conversion is also called isomerization.

The analysis presented here includes calculations of the optimized energies, vibra-

tional frequencies, and infrared intensities that were carried out at the Hartree–Fock

Bio-molecular devices for terahertz frequency sensing 65

(HF) level within the split valence polarized 6-31G(d) basis set in the Gaussian 98 pack-

age [31]. The energies of the excited states were found within the single configuration

interaction approach (CIS), where one models the first excited state as combinations of

a single substitution from the highest occupied molecular orbital (HOMO) to the lowest

unoccupied molecular orbital (LUMO). Vibrational frequencies were then computed by

determining the second derivatives of the potential energy with respect to the Cartesian

nuclear coordinates and then transforming to mass-weighted coordinates. Due to the fact

that electron correlation is neglected, the frequencies computed using the HF approxi-

mation are known to be overestimated by approximately 10–12%. Furthermore, because

a medium-sized basis set was used, the derived values can be expected to deviate even

more from experiments, i.e., by approximately 15% in total [32]. Therefore, a scaling

was performed on the originally calculated frequencies by an empirical factor of 0.893

to eliminate known systematic errors in the physical model.

To monitor the process of isomerization from trans-2-butene to cis-2-butene, the

torsional angle , defined as the dihedral angle of the plane of C1–C2–C3 and the

plane of C2–C3–C4 around the double bond in the C1–C2

C3–C4 chain associated

with the molecule given in Figure 6(A), was taken to be the reaction coordinate. The

potential energy (PE) curves associated with the isomerization process for the ground

 and the first excited singlet state (S

) of 2-butene are shown in Figure 6(B), along

(B)

(A)

θ = 180°, trans-2-butene θ = 0°, cis-2-butene

20 40 60 80 100 120

140 160 180

Torsional angle (degree)

Energy (eV)

cis- trans-

Figure 6 (A) Geometrical structure of trans-2-butene and cis-2-butene; (B) Potential energy

curves associated with the isomerization process which involve the ground-state, S

, and the first

excited-state, S

. Arrows depict the energy-path of the molecules

66 Ying Luo et al.

with the next two excited states S

and S

. Here it is important to note that the trans-2

geometry (i.e.,  = 180



) is the natural-state and the cis-geometry (i.e.,  = 0



)isthe

metastable-state. Without external excitations, the large PE barrier 1.98 eV in the ground

state prevents the transition from trans-2-butene to cis-2-butene. It is also clear from

Figure 6(B) that there is no barrier in the first excited singlet state S

, which is ideal for

an ultra-fast switching between the trans- and cis- isomers.

Potential energy curves can be used to illustrate this optically induced isomerization

process by following the superimposed arrows. The process begins with a required

optical excitation (∼846 eV, 146 nm) of the “electronic-state” of the trans-geometry

from S

to S

. This is followed by a non-radiative decay to the S

PE valley minimum,

which corresponds to a 90



rotation about the reaction coordinate. At this point, the

molecule undergoes an “electronic” radiative decay from S

to S

. This is followed by

a second non-radiative decay to the cis-geometry, which corresponds to a second 90



rotation about the reactive coordinate. At this point, butene will remain in the metastable

cis-2 geometry until thermal relaxation of the system back to the ground state.

To estimate the probability that the excited trans-2-butene will follow the isomer-

ization process described above, instead of relaxing back to its own ground state, we

investigate the molecular dynamics of butene in the first singlet excited state S

combining the theory of Newton’s Dynamics and standard quantum chemistry software

Gaussian 98. We began the investigation from cis-geometry ( =0



 and calculated the

time for the excited cis-geometry to achieve the energy minimum ( = 90



 and the

excited trans-geometry ( =180



 of S

. The calculation procedure is as follows: (i) we

calculated the potential energy of the ground state and the excitation energy of S

of the

optimized cis-butene using Gaussian 98 package and by adding the two energies we got

the potential energy of the excited cis-butene. Note that we took this potential energy as

the total energy of butene ( i.e. we assume the kinetic energy of excited cis-butene is 0).

To initiate the rotation, we actually started from a very small  with a very small initial

velocity. (ii) For every 10



, we calculated 20 points (i.e., we performed Gaussian 98

calculation every 05



). For every point, we calculated the ground-state energy without

optimization and the corresponding excitation energy; thus we got the potential energy

of the excited state. By subtracting the potential energy from the total energy, we got

the kinetic energy. Then we used the energies of 20 points to calculate the time for

butene to rotate 10



by integrating Newton’s equations.

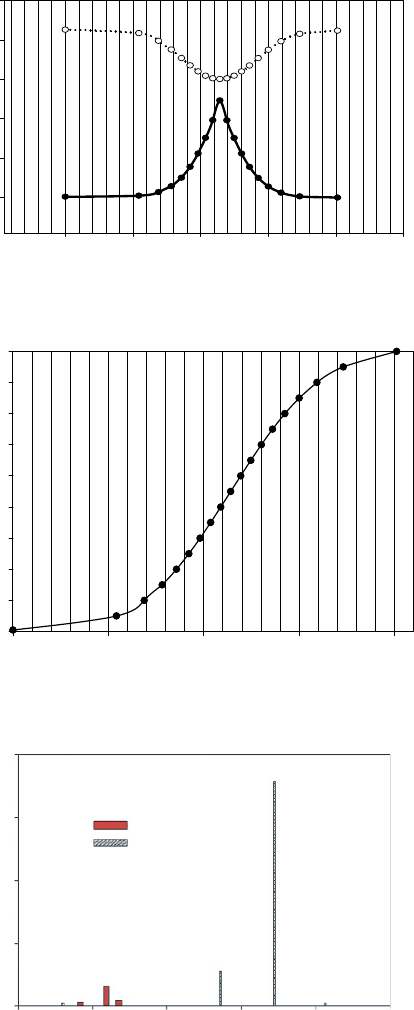
The relation between the potential energies of excited states and time is given in

Figure 7, and for demonstrative purposes, the PE curves of the ground state S

presented on the same graph. We can see that the time for excited trans-2-butene to

relax to the valley minimum is about 100 fs and symmetrically it takes almost the same

time to go from the minimum to cis-2-butene. On the other hand, according to the

spontaneous emission theory the time for excited trans-2-butene to relax back to ground

state is about 59 ×10

s. So the isomerization process will be significantly probable.

In Figure 8, we demonstrate how the dihedral angle of C1–C2

C3–C4 double bond, or

the geometric structure of butene, will change with time.

The lowest vibrational frequencies and the associated IR intensities that were cal-

culated for trans-2-butene and cis-2-butene are compared in Figure 9. These results

indicate a significant difference in spectral signatures of the two molecular conforma-

tions and one that has the general quantitative characteristics needed by the previously

discussed bio-molecular architecture.

Bio-molecular devices for terahertz frequency sensing 67

Time (fs)

Energy (eV)

0 50 100 150 200 250

Figure 7 Molecular dynamics of butene: Energies of first singlet excited state vs. time

Time (fs)

Dihedral Angle θ (Degree)

100

120

140

160

180

0 50 100 150 200

Figure 8 Molecular dynamics of butene: Dihedral angle vs time

0 200 400 600 800 1000

Vibrational frequencies (cm

–1

)

IR intensities (km /mole)

trans-2-butene

cis-2-butene

Figure 9 The calculated characteristics of the lowest spectral signatures of trans-2-butene and

cis-2-butene [1]

68 Ying Luo et al.

Table 1 A comparison of calculated spectral signatures with measurements of McKean et al. [33]

cis-2-butene trans-2-butene

McKean el al. [33] Calculated in this

work

McKean et al. [33] Calculated in this

work

566 5442 239 2360

686 6878 284 2712

865 9342 9643 9568

970.9 9973 9788 9907

1009.1 10516 10468 10254

1036.9 11296 10636 10529

1268.5 13663 1303 13006

1383.8 14051 13822 13989

1408.4 14173 14474 14519

1444.5 14581 1461 14669

1456.2 14602 28356 28489

1458.9 14669 2871 28900

1669 17029 2890 28901

2893.2 28529 29325 29176

2900.8 28558 29494 29573

2914.5 28919 2973 29619

2929.5 29325

2947.5 29514

2954.1 29556

2979.2 29798

Table 1 compares the calculated frequencies to prior experimental measurements of

McKean et al. [33]. One can see that all the absorption frequencies calculated in this

work are reasonably-good agreeable (i.e., within ∼3%) with the experimental results.

While this study yielded qualitative bio-molecular function of the type needed for

the proposed architecture, the required excitation from S

to S

is far too large (i.e.,

∼85eV) to be practical, and the associated spectral bio-signatures are well above the

THz regime where species-specific information is expected to be present. Hence, the

alternative molecule retinal will now be considered, which is known to be visible-

frequency light sensitive, and which is more complex and can be expected to yield much

lower frequency vibrational modes.

All-trans-retinal is the chromophore of bacteriorhodopsin, the light transducing pro-

tein in the purple membrane of Halobacterium salinarium. The isomerization from

all-trans to 13-cis conformation takes places very quickly in approximately 500 fs [34]

induced by absorption of a 568 nm photon [35]. 11-cis-retinal is the chromophore of

rhodopsin. The ultra-fast (in ca. 200 fs [34]) photoisomerization from 11-cis-retinal to

all-trans-retinal conformation has been elucidated as induced by absorption of a 498 nm

photon [35]. Besides 11-cis-retinal and 13-cis-retinal, 9-cis-retinal is also a geomet-

ric isomer of all-trans-retinal and derives from the rotation of all-trans-retinal around

C10 double bond by 180



although 11-cis-retinal and 13-cis-retinal derive from

the rotation of all-trans-retinal around C11

C12 and C13

C14 double bonds.

Bio-molecular devices for terahertz frequency sensing 69

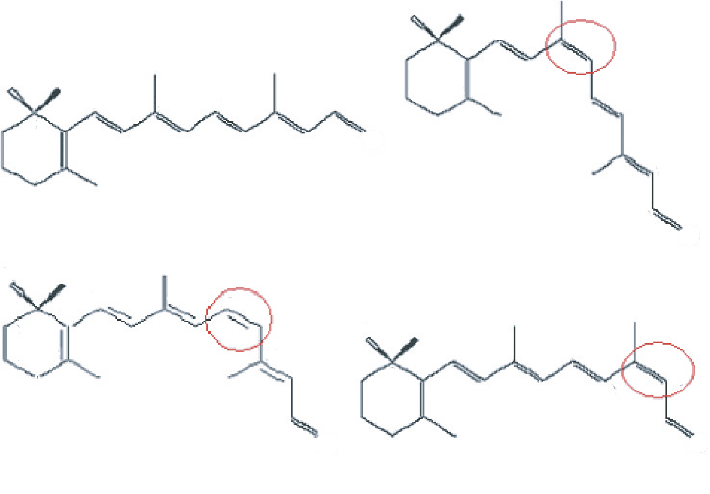
(A) all-trans-retinal (B) 9-cis-retinal

(D) 13-cis-retinal(C) 11-cis-retinal

Figure 10 Geometric structures of retinal isomers

The geometric structures of all-trans-retinal and its isomers are shown in Figure 10.

The retinal has two properties which make it very interesting for our studies. First,

the electrons in retinal readily absorb photons in the visible range of wavelengths

(400–700 nm) which means the molecule can be optically induced into excited-states.

Second, as this study will show, the lowest vibrational frequencies are in THz region.

2.2.2. Simulation and analysis of retinal isomers

The vibrational spectra were calculated at Hartree–Fock method within split valence

polarized 6-31G(d) basis set using Gaussian 98 package. All calculated frequencies were

multiplied by empirical factor 0.893 to eliminate the known systematic errors. The very

far infrared (FIR) spectra (under 30 cm

−1

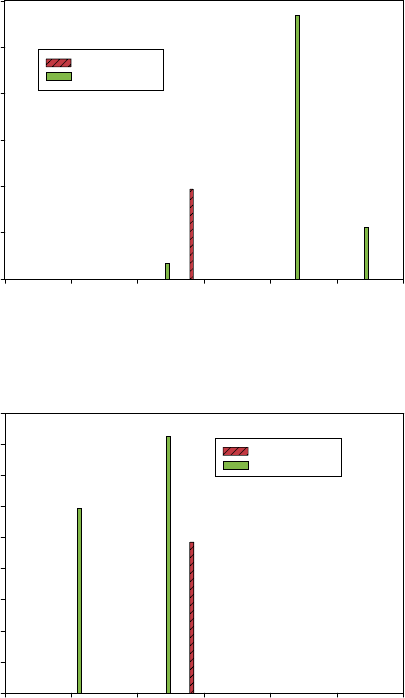
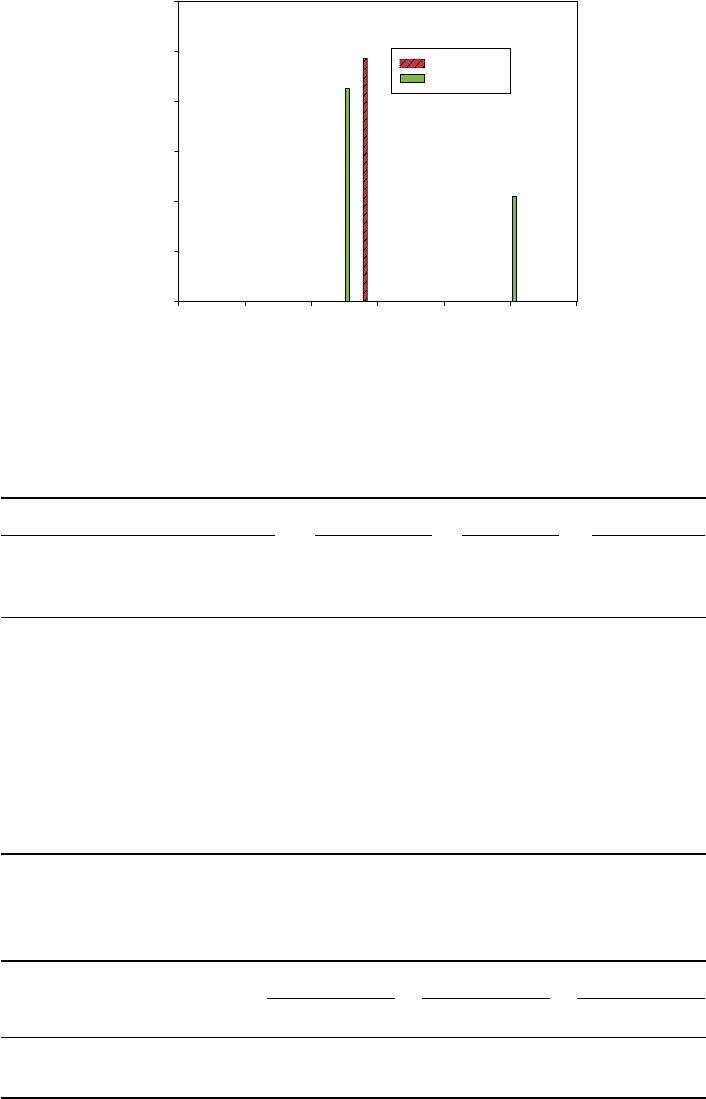
) of four isomers are shown in Figures 11–13.

These results illustrate that the various metastable-state conformation yields spectra

fidelity (e.g. 22 cm

−1

in 9-cis,12cm

−1

in 11-cis,26cm

−1

in 13-cis) that can be used

in defining multiple communication channels and for realizing the MS

approach to

expand the amount of bio-signature information. We compared our theoretical vibra-

tional frequencies with the density functional calculations of Gervasio [36], and also

with the experimental data measured by THz time-domain spectroscopy at 10 K [37]

and by FTIR spectrometer at 15 K [36]. As shown in Table 2, the frequencies pre-

dicted in our simulation are in very good agreement with the calculations of Gervasio

and comparable to experimental data above 40 cm

−1

. It is noteworthy that vibrational

modes under 40 cm

−1

exist in both simulations but are not available in experimental

70 Ying Luo et al.

Vibrational frequency (cm

–1

)

0.0

0.5

1.0

1.5

2.0

2.5

3.0

all-trans-IR

9-cis-IR

0 5 10 15 20 25 30

IR intensity (km/mol)

Figure 11 FIR spectra of 9-cis-retinal and all-trans-retinal (<30cm

−1

) [2]

Vibrational frequency (cm

–1

)

0.6

0.4

0.2

0.0

0.8

1.0

1.2

1.4

1.6

1.8

0 5 10 15 20 25 30

IR intensity (km/mol)

all-trans-IR

11-cis-IR

Figure 12 FIR spectra of 11-cis-retinal and all-trans-retinal (<30 cm

−1

) [2]

measurements. This can be explained by the experimental difficulties in the range of

40 cm

−1

and below.

This research effort also generated results for the potential energy barriers between

the ground state and metastable-state conformations (which are important for specify-

ing switching times) and the electronic excited-state energies (which are needed for

specifying the necessary optical excitation).

Calculations of the potential energy curves (PEC) in the ground-state S

were carried

out at both HF theory and density functional theory (DFT) levels with the split valence

polarized 6-31G(d) basis set using the Gaussian 98 package [31]. The B3LYP density

functional was used, which is Becke’s three-parameter hybrid functional using the

Lee, Yang, and Parr (LYP) correlation functional [38]. We calculated the energy of

9-cis-retinal, 11-cis-retinal, 13-cis-retinal and all-trans-retinal isomers and simulated

the rotation of all-trans-retinal around C11

C12, C13

C14, and C9

C10 double

Bio-molecular devices for terahertz frequency sensing 71

Vibrational frequency (cm

–1

)

0.4

0.2

0.0

0.8

0.6

1.0

1.2

0 5 10 15 20 25 30

IR intensity (km/mol)

all-trans-IR

13-cis-IR

Figure 13 FIR spectra of 13-cis-retinal and all-trans-retinal (<30 cm

−1

) [2]

Table 2 Vibrational frequencies of isolated retinal isomers in the range of FIR spectra (cm

−1

)

All-trans-retinal 9-cis-retinal 11-cis-retinal 13-cis-retinal

Ref.

[37]

exp

Ref.

[36]

exp

Ref.

[36]

cal

This

work

Ref.

[37]

exp

This

work

This work Ref.

[37]

exp

This

work

17 141 12.2 56 12.7

29 300 22.0 123 25.3

35 308 27.2 305 30.3

46.6 46 49 427 43.5 337 41.7 47.7

54.4 53 59 575 53.9 54.0 544 54.8 58.5

61.0 59.9 627 61.0

66.2 64 64.8

69.3 68 78 755 81.1 68.6 75.2

90.6 89 99 960 92.8 942 98.8

1000

Table 3 Energy barrier in the PECs of isolated retinal in the ground state (eV)

C10 C11

C12 C13

C14

HF B3LYP HF B3LYP HF B3LYP

Barrier between 0



and 90



1.8360 1.4334 1.4878 1.1859 1.6728 1.2974

Barrier between 90



and 180



1.8578 1.4634 1.7517 1.4035 1.6946 1.3274

72 Ying Luo et al.

Torsional angle θ

11 12

(degree)

0.0

0.2

0.4

0.6

0.8

1.0

1.2

1.4

1.6

1.8

2.0

DFT

0 20 40 60 80 100 120 140 160 180 200

Energy of molecule (eV)

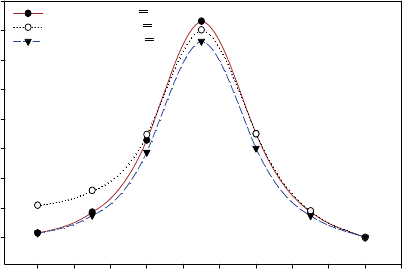
Figure 14 PECs of all-trans -retinal rotating around C11=C12 double bond calculated at HF

and DFT level

bonds. We took the dihedral angles of the corresponding double bonds 

C11=C12



C13=C14

and 

C9=C10

as the reaction coordinates which were fixed during the optimizations,

although all other parameters were free. The PECs of the ground state of rotation around

C11

C12 double bond calculated at both HF and DFT levels are shown in Figure 14.

According to our calculations, the results at the DFT level qualitatively agree with

those at the HF level although they achieve better accuracies by including electron

correlation. Also, both results predict significant barriers in the ground state that prevent

the transition from one isomer to another without external excitation.

In addition, PECs of the ground state of rotation around C9=C10, C11=C12, and

C13=C14 double bonds at DFT level are shown in Figure 15. It is clear that all-trans-

retinal has the smallest energy among all retinal isomers and is the most stable confor-

mation of retinal. 11-cis-retinal, 13-cis-retinal and 9-cis-retinal are local minima on the

PECs which means they are metastable conformations. Rotation around C9=C10 double

bond has the biggest barrier and around C13=C14 has the smallest barrier. The complete

list of barriers of the three isomerizations in the ground states are illustrated in Table 3.

To investigate the external conditions (proper light frequency) needed to initiate the

isomerization processes, we calculated the low-lying excited-states of all-trans-retinal

and its isomers. The energies of the excited states as shown in Table 4 are found within

time-dependent DFT (TDDFT) methods. For molecules with low-lying excited-states,

Table 4 Excitation energies of retinal isomers calculated with TDDFT method (eV) and OS

represents oscillator strength

9-cis-retinal 11-cis-retinal 13-cis-retinal All-trans-retinal

E(eV) OS E(eV) OS E(eV) OS E(eV) OS

3.0708 0.9110 3.0490 1.0821 3.0673 1.0771 3.0496 1.2225

3.0833 0.0006 3.0505 0 3.0991 0.0002 3.0646 0.0054

3.8894 0.5567 3.8612 0.5131 3.9118 0.5023 3.8893 0.5745

Bio-molecular devices for terahertz frequency sensing 73

rotation around C9 C10

rotation around C11 C12

rotation around C13 C14

Torsional angle θ (degree)

1.6

1.4

1.2

1.0

0.8

0.6

0.4

0.2

0.0

0 20 40 60 80 100 120 140 160 180 200

Energy of molecule (eV)

Figure 15 PECs of the ground state of all-trans-retinal rotating around C9==C10, C11==C12,

and C13==C14 double bonds at DFT level

TDDFT makes a considerable improvement over HF-based methods (like CIS) [39].

The excitation energies are similar for the corresponding states of these four isomers and

the lowest excitation energies 3.07 eV (ca. 403 nm) are in the visible region. The similar

excitation energies show that our existing simulations are not sufficient to explain the iso-

merization mechanism around different double bonds. As mentioned before, in rhodopsin

the isomerization from 11-cis-retinal to all-trans-retinal occurs but in bacteriorhodopsin

the isomerization from all-trans-retinal to 13-cis-retinal takes place. So the proper envi-

ronments, such as protein environment in this case, probably play the most important

role in determining which double bond participates in the isomerization process.

3. Retinal nanostructure arrays

Monolayers of retinal immobilized on solid substrates are of considerable importance

not only for applications as retinal-based sensors but also for investigations of the

complex behavior of retinal molecules at interfaces. By modifying one end of retinal

with a thiol linker, we could chemically graft the retinal to gold surfaces. Because

two-dimensional gold nanostructure arrays can be produced on highly oriented pyrolytic

graphite (HOPG) surfaces [40] and on semiconductor substrates [41], we can finally

fabricate two-dimensional retinal nanostructure arrays. In addition, by controlling the

two-dimensional spatial distribution of gold nanostructures including shapes and sizes,

we can control retinal molecules quantitatively.

3.1. Two-dimensional nanopatterned retinal structure

Two-dimensional nanopatterned retinal structures can be created in the following three

steps. First, connect retinal to cysteine (amino acid) which contains the thiol group by

nucleophilic addition-elimination reaction between aldehyde (C

O) and primary amine

(–NH

) as described in most organic chemistry textbooks such as [42]. The reaction is

shown in Figure 16 with the product N -retinylidene cysteine.