Seetharaman S. Fundamentals of metallurgy
Подождите немного. Документ загружается.

grains in a polycrystalline material (Ashby 1971). For spherical, hard particles in
a soft matrix the effect is given by a geometrical slip distance, g
0
, proportional to
f =r (fraction over particle radius). The geometrical slip distance will vary with
the shape of the constituents. The flow stress can then be described by a law of
mixtures. This approach has been successful in the description of the flow stress
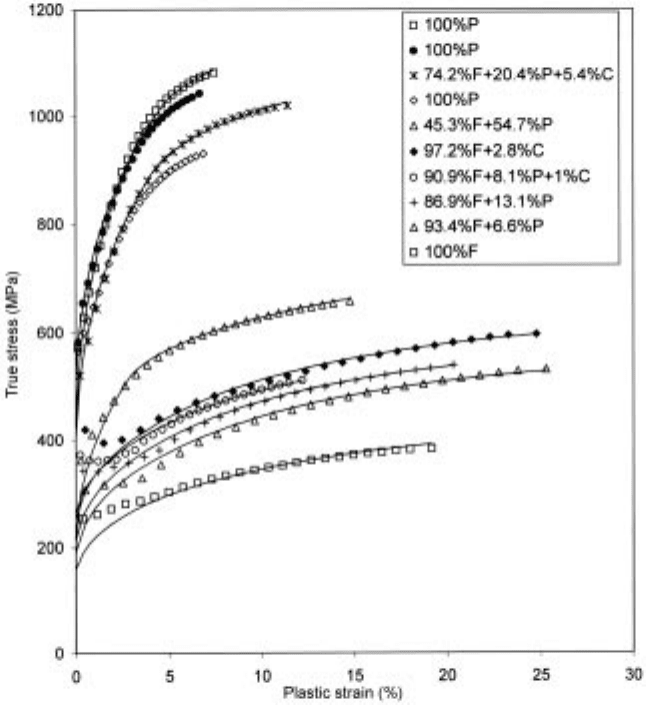
for dual phase steel as well as for ferritic perlitic steels, see Fig. 11.1 (Engberg
and Carlsson 2002; KoÈmi et al. 2004). For steels with TRIP (transformation
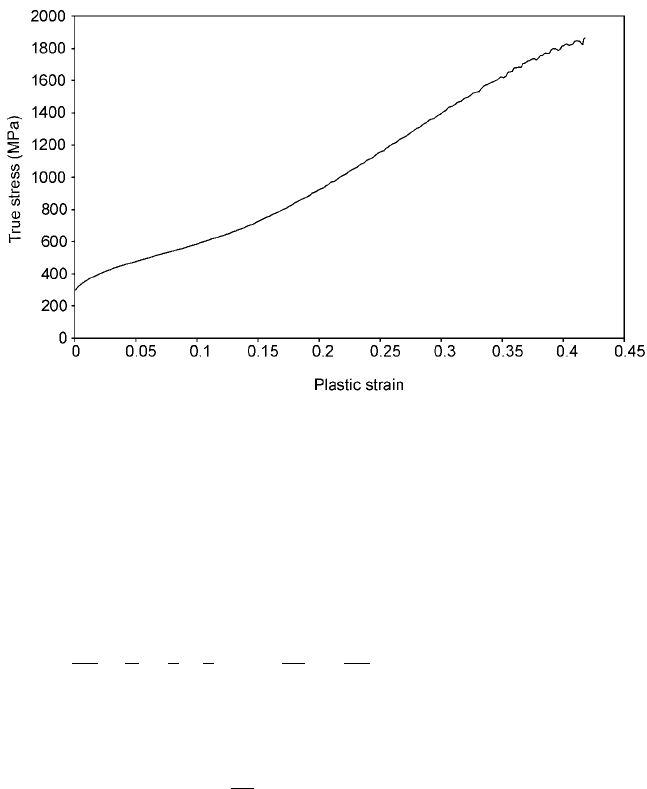
induced plasticity) properties the increase in hardening is substantial. In Fig.
11.2 one example is given showing the effect of martensite formation in a 304-
type stainless steel.
11.1 Lines: model, points: observations. F ferrite with different amounts of
pearlite, P and cementite, C.
456 Fundamentals of metallurgy
The flow stress can now be expressed by
X
f
i
i
for constant strain 11:6
X
f
i
i
for constant stress 11:7
i
0i
mGb
i
p
11:8
d
i
dt
m
b
1
L
1
d
g
i
d
i
dt
d
i
dt
recovery
11:9
where g
i
is the geometrical slip distance caused by the difference in plastic
deformation of phase i and all other constituents, j.
g
i
X
j
g
0j
1 ÿ
d
j
d
i
11:10
11.3 Rate effects
The strain rate sensitivity is important in the distribution of plastic strain. The
effect on the magnitude of the flow stress is also of importance, for example, in
crash members in automobiles, in deciding the roll forces needed during skin-
pass rolling, etc. The rate dependence is due to thermally activated deformation
(Peierls±Nabarro barriers, solute atoms, etc.) at low to ambient temperatures,
below 0.5 T
m
, and to diffusion controlled processes (climb, recrystallisation) at
higher temperatures.
11.2 Tensile test of 304-type stainless steel.
Analysing metal working processes 457

11.3.1 Low to ambient temperatures
Thermal barriers for dislocation slip can, as indicated, be overcome by thermal
activation. This can only be true for sufficiently small barrie rs such as given in
Table 11.2. The work needed to overcome the barrier can be written as
H H
0
ÿ
Z
A
0
dA 11:11
where H
0
is the work needed without the assistance of applied stress,
the
stress in excess of athermal barriers (thermal stress) and A the activation area
(length of dislocation times distance travelled during the activation event). The
strain rate obtained at a given thermal stress is then given by the product of the
mobile dislocation density,
m
, the attack frequency, !, and the probability of
overcoming the barrie r (as given by an Arrhenius expression). The shape of the
barrier and the mobile dislocation density will then give the thermal stress. For
ferritic steels a good approximation of the Peierls±Nabarro barrie r is obtained by
putting the activation area inversely proportional to the thermal stress and to
assume a constant mobile dislocation density. This will lead to a simple relation
d
dt
c
1
c
2
T=c
3
11:12
where c
i
are constants. For fcc metals the Peierls±Nabarro barriers are normally
small and the effect is quite small (can often be neglected). For bcc and
hexagonal (hcp) metals the effect can be quite large.
Atoms in solid solution can play a significant role. In ferrite a strong elastic
interaction is found for interstitial atoms (C, N) while substitutional atoms give a
considerably smaller contribution. In fcc metals they can contribute substan-
tially. In dilute solutions the atoms can be regarded as point obstacles with the
barrier give n by the elastic interaction. If the barriers are strong, then the
dislocations are best described as partially flexible and the Friedel process (see,
for example, Brown and Ham 1971) can be assumed to prevail. For C in ferrite
this will lead to an expression of the form
Table 11.2 Approximate activation areas for some thermally activated
barriers
Mechanism Normalised activation area, A/b
2
Peierls-Nabarro 10±100
Cutting of forest dislocations 100±10 000
Non conservative motion of jogs 100±10 000
Cross-slip 10±100
Solute atoms 10±100
458 Fundamentals of metallurgy

1 c
2
T ln
d
dt
c
3
0
B
@
1
C
A
2
6
4
3
7
5
3
c
1
G
x
p
11:13
where x is the atomic fraction of carbon. c
i
are material parameters (Engberg and
Carlsson 2002).
Static strain ageing in ferritic steels gives rise to the Lu
È
ders' strain during
tensile testing. The localisation of strain to the band(s) gives local strain rates
much in excess of the nominal ones. The sharper the plastic front, caused, for
example, by a finer grain size where the indivi dual grain boundaries constitute
barriers for front movement, the higher the strain rate and consequently the
higher is the yield stress and the yield elongation. With an increased nominal
strain rate the yield stress increase is larger than what is obtained during
homogeneous deformation (see, for example, Yoshitake et al. 1996). This is of
importance, for example, during skin-pass rollin g, where commonly a fixed total
elongation is prescribed, at accelerations or decelerations giving rise to
substantial changes in needed roll force.
11.3.2 Warm to hot working temperatures
Above around 0.3 T
m
recovery by cross-slip mechanisms are thought to occur
and above 0.5 T
m
climb becomes significant. This has a very significant effect on
the temperature and strain-rate dependency of the flow stress. Also, recrystal-
lisation will become of importance. The dislocation generation mechanisms will
remain as given above. It has, however, been suggested that the generation of
point defects, vacancies, due to cutting of forest dislocations or other dislocation
interactions can be of importance as this will increase the diffusivity. One classic
example of this effect is found in dynamic strain ageing of substitutional alloys.
In Fig. 11.3 one example of the phenomenon is shown for a 316-austenitic
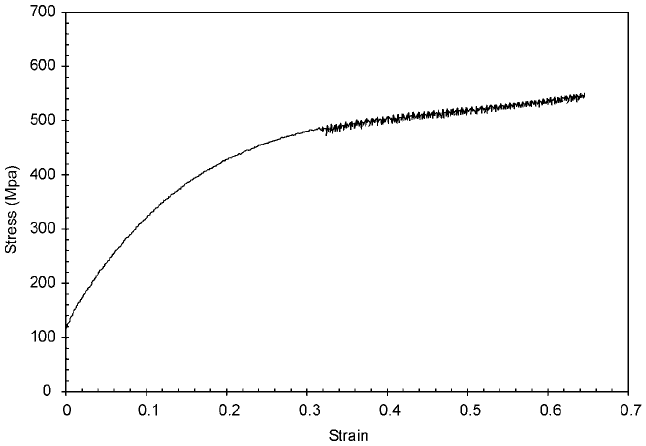
stainless steel deformed at 400ëC. The effect increases with strain as more
vacancies are created and the diffusivity increases.
The generation of vacancies is also counteracted by diffusion to various
sinks, such as dislocations, grain boundaries, etc. A simple description is given
by
dx
v
dt
c
1
b
d
dt
p
ÿ c
2
D
m
x
v
x
v
ÿ x
v0
p
11:14
where x
v
is the vacancy conce ntration, x
v0
the same at thermal equilibrium, D
m
the migration part of the diffusion coefficient and c
i
are material parameters
(Siwecki and Engberg 1997). The first term on the right-hand side gives the
generation and the second term the annihilation of vacancies.
Recrystallisation is traditionally described by a JMAK (Johnson-Mehl,
Awrami, Kolmogorov) type expression combined with regression formulas for
Analysing metal working processes 459
the influence of strain, strain rate, alloy composition, etc. New grains appear on
grain and phase boundaries and on shear bands (see, for example, Sellars 1997).
It has been suggested that subgrains take an active part in the nucleation process
of new recrystallised grains. Humphreys (1997) proposed that a part of the
subgrains could undergo abnormal growth and that for some critical size of the
abnormal subgrains they were sufficiently large to be able to grow as new
grains. This idea was tested on a stainless steel (Wang et al. 2003) with
seemingly good results. The possibility of subgrains acting as nuclei for
recrystallisation should, of course, also be valid during deformation but here the
subgrain size is decided by the deformation conditions and the material
properties.
Preliminary results from applying a slightly modified version of the model
have been tried on a CMn-steel, see Fig. 11.4. Here we allow one deformed grain
size and one recrystallised. The flow stress is given by a law of mixtures and is
also affected by the need for geometrically necessary dislocations when the softer,
recrystallised part constitutes a continuous network. As is seen the major features
of both flow stress, including dynamic recrystallisation, and recrystallised fraction
are described. In fact, the figure display dynamic and metadynamic
recrystallisation (starts during deformation and is completed after deformation).
After deformation we also see the characteristics of a stress relaxation experiment,
as performed by deforming to a given strain and then stop the testing machine and
keep the total strain constant. First, the softening is rapid while recrystallisation
still takes place and then we just see the effects of recovery.
11.3 Dynamic strain ageing in a 316-type stainless steel.
460 Fundamentals of metallurgy
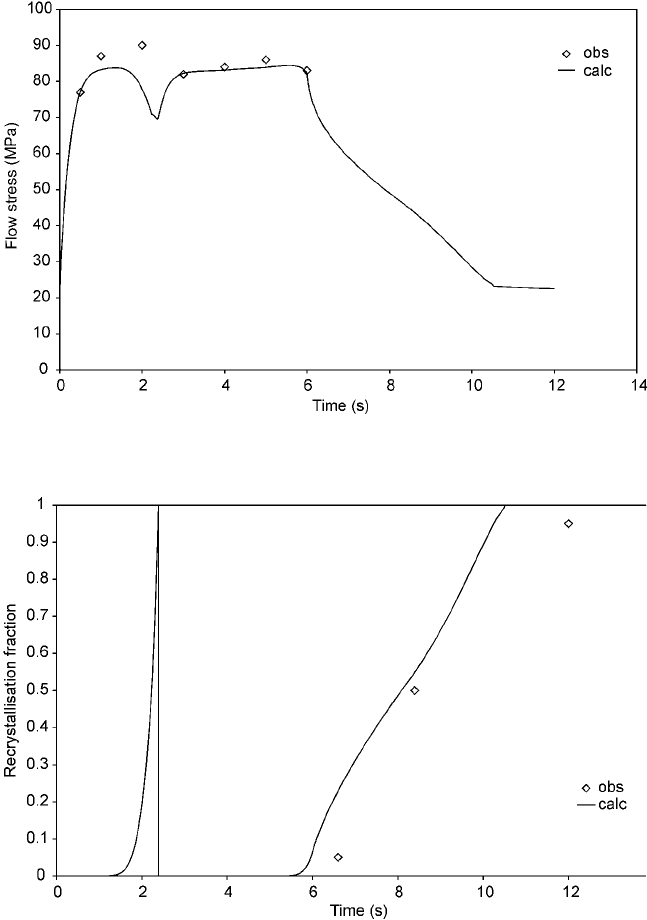
11.4 Comparison of model calculations with experimental data for
recrystallisation and flow stress in a CMn-steel (Karjalainen and Perttula 1996).
Analysing metal working processes 461
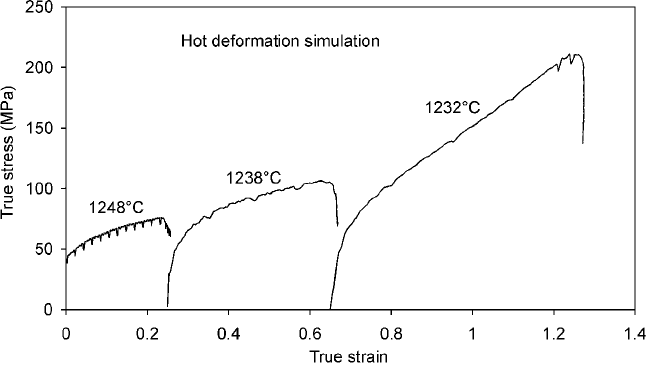
11.4 Interaction with phase transformations
During hot deformation, phase transformations can also occur. Microalloying
with Ti, Nb and V has been successfully used to produce high strength hot-rolled
steel for several decades. Precipitation o f (Ti,Nb)(C,N) takes plac e on
dislocations during hot rolling and gives significant effects by retarding and
even completely stopping recrystallisation. In Fig. 11.5 one example is given
where the flow stress is clearly affected by precipitation in the third consecutive
deformation step.
The effect of precipitation is fourfold:
·
it gives precipitation hardening;
·
it retards and eventually blocks recovery;
·
it retards and eventually blocks recrystallisation;
·
it retards and eventually blocks grain/phase boundary movement.
The ability to block recrystallisation has been utilised in controlled rolling of
HSLA steel. The purpose is to obtain heavily deformed austenite grains,
`pancakeing', with strain accumulated in several of the last passes. The
subsequent phase transformation then yields a fine ferrite grain size and
correspondingly good properties.
So far we have mainly discussed precipitation but, of course, phase trans-
formations can also occur on a more massive scale. For ferritic steels it is the
transformation from austenite to ferrite or ferrite plus carbide. For very low
carbon steels the temperature interval for the transformation is small and thus
large changes in volume fractions can occur. As ferrite is considerably softer
than austenite at a given temperature, the flow stress drops significantly with
11.5 Hot compression tests, performed at SIMR, of a Ti-Nb HSLA steel.
462 Fundamentals of metallurgy
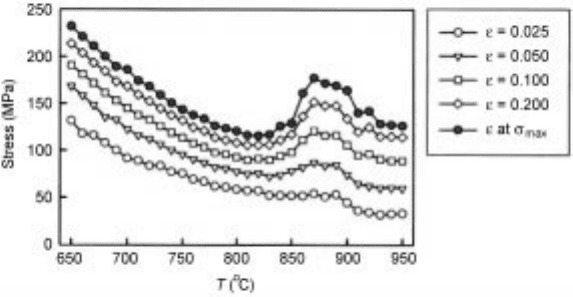
increasing volume fraction of ferrite. The flow stress behaviour has been studied
extensively. A simple law of mixtures seems to catch the main changes,
although as discussed above it is expected that when austenite is the minority
phase in a continuous matrix of ferrite, an increase in work hardening should be
obtained. In Fig. 11.6 one example is given for a 0.05% C steel, where, also, the
increased work hardening is obvious.
11.5 Examples of material behaviour during
processing
The intention here is to give some examples of material behaviour during
processing. All examples are taken from SSAB Tunnpla
Ê
t AB.
11.5.1 Hot rolling
Mill data from the hot strip mill has been used to calculate the mean flow stress in
each pass, assuming the material to be elastic ± ideally plastic. The roll force model
used was a classical slab method with constant friction assumed in the roll gap. For
the roughing mill (reversible 4-high) both roll force and roll torque were available
so the friction coefficient could be evaluated in addition to the flow stress for each
pass. The values were close to 0.3 so it was decided to use this for all calculations,
also for the finishing, six-stand (4-high), tandem mill. As torque is not measured in
the finishing mill only flow stress values could be obtained for this part.
Hot compression test results for CMn-steels have been collected and evaluated
at the Swedish Institute for Metals Research (SIMR) (Sandberg and Siwecki
1985). The data for the CMn-steels were obtained in the temperature range 800±
1200ëC and the strai n-rate interval 0.001±1100 s
ÿ1
. The carbon and manganes e
contents varied between 0.01±0.19% and 0.2±1.5% respectively. From the
regression formulas of this analysis mean flow stress values corresponding to
11.6 Flow stress from hot compression tests of a 0.05% C steel (Bodin 2002).
Analysing metal working processes 463
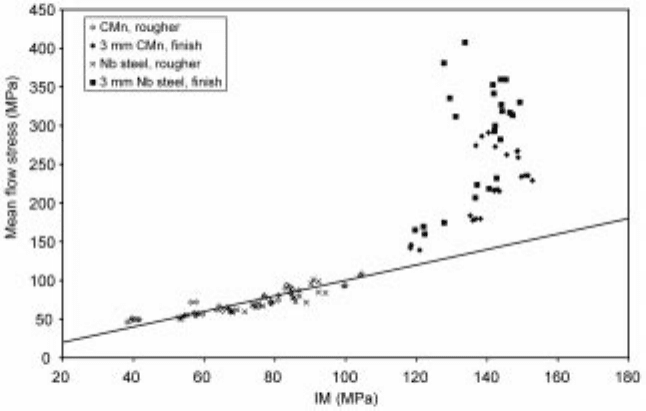
strains, strain-rates and temperatures for the same rolling passe s as above have
been calculated. The hot compression data were all of single stroke type, meanin g
that the starting structure was fully recryst allised in all cases.
In Fig. 11.7 results for one CMn-steel and one Nb-microalloyed steel are
displayed. During roughing the two types of data coincide, meaning that
complete recrystallisation is obtained between the successive passes. In the
finishing mill the two datasets start to diverge. This can only be interpreted as
the result of strain accumulation between successive passes, interpass times are
not sufficiently long to allow complete recrystallisation. The effect is stronger
for the microalloyed steel due to the presumed effect of str ain induced
precipitation of niobium carbonitrides.
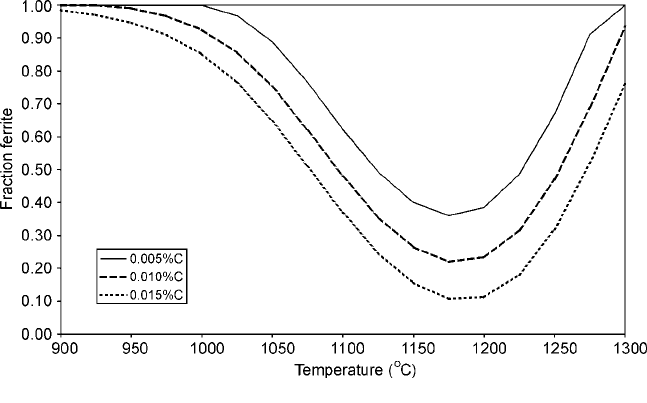
During rolling of high silicon steel (used for their magnetic properties) the
material behaviour has sometimes caused problems with unexpected increases in
width during roughing. The reason for this was found in variations in the
temperature of the slab as it entered the mill and was due to the position of the
slab in the reheating furnace. If the first end of the slab was close to a skid mark
then the temperature was 20 to 40 degrees lower than usual. An examination of
the phase diagram shows that this will lead to an increased amount of ferrite and
consequently to a softer material, see Fig. 11.8.
11.5.2 Cold rolling
As a part of an ECSC project (Vanel et al. 2004) a set of experiments were
conducted in the five-stand tandem mill at SSAB Tunnpla
Ê
t. The mill was run at a
11.7 Calculated mean flow stresses from mill data.
464 Fundamentals of metallurgy
low speed of 30 m/minute and emergency stopped. This enabled us to extract
material before and between the stands and after the last stand. This material was
then carefully characterised by tensile testing in three different directions in the
plane of the sheet (along the rolling direction , RD, transverse to the rolling
direction, TD, and 45 degrees in between). Tests were also performed by
compression testing in the normal direction (performed on stacks of sheet by
SIMR). Finally, the material was also characterised by texture measurements
and calculations of Taylor factors (and also by SIMR).
In Fig. 11.9 results from tensile testing of a 0.45% C steel in the rolling
direction are displayed. The change in deformation from rolling to uniaxial
tension gives a change in the yield surface, causing yield at a lower stress than
would be expected if the material showed isotropic hardenin g in accordance to
previous fin dings (see, for example, Koc ks et al. 1998; Granlund 1997). The
isotropic yield surface is then approached as deformation continues and we have
assumed that the transient effects are overcome when R
m
is reached in the
tensile tests.
The next step was to bring all data together in a total descrip tion. The first
obvious trial was to use the Taylor fact ors depicted from the texture
measurements. This, however, was not successful. In a second trial we simply
used the Hill yield criterion,
p
1
11
ÿ
22
2
p
2
22
ÿ
33
2
p
3
33
ÿ
11
2
2 p
4
2
12
2 p
5
2
23
2 p
6
2
31
k 11:15
with much better success. The result is shown in Fig. 11.10 where data from all
types of tests are displayed in the form of the plane strain flow stress. It also
11.8 Volume fraction of ferrite for a 1.85% Si steel. Calculated by ThermoCalc.
Analysing metal working processes 465
