Seetharaman S. Fundamentals of metallurgy
Подождите немного. Документ загружается.


diagram, the rate of mixing in the liquid and the diffusive flux into the solid. This
leads to the condition that both the liquid and solid compositions can be transient
and gross changes in composition are possible during solidification.
For example, under equilibrium conditions where mass transfer is rapid in
both liquid and solid the final composition of the solid will be the composition
of the liquid; however, in conditions where diffusion in the solid is very slow
and can be ignor ed, the compositional profile will be described by the Gulliver
Scheil equation:
C
s
kC
0
1 ÿ f
s
kÿ1
10:76
where the composition of the solid will vary continuously from solidification
start to finish. In castings this variation is seen perpendicular to the growth
direction of a cell or dendrite and leads to phenomena of segregation. As it is
possible for solute to increase in the liquid between cells or dendrites, the last
solidification temperature of a casting is determined by this segregation and the
effective solidus temperature is a function of the phase diagram and the local
thermal and mass fields. For this reason there are many models that have been
developed to allow this determination and numerical solutions are necessary to
determine the segregation amount accurately.
The interface temperature is also strongly affected by composition (equation
10.43) and, in alloy solidification where heat transfer is important, any change in
interface composition will result in a change in interface temperature.
The phenomenon of interface instability was explained in detail by Mullins
and Sekerka, where, following the approach of Kurtz, the marginal stability
criterion can be written as follows:
ÿÿ!
2
ÿ
k
l
G
l
l
k
s
G
s
s
mG
c
c
0 10:77
where ! is 2=, is the wavelength of a small perturbation,
k is an average thermal
conductivity for the liquid and the solid, is a term to correct the thermal and
compositional terms due to local interface conditions, m is the slope of the liquidus
and G
c
is the compositional gradient in the liquid. In this equation terms that are
negative favor a planar interface, while positive terms favor instability of the
interface. In this case a gradient of composition in the liquid always favors
instability as does a negative thermal gradient in the liquid. Thus alloys and under-
cooled liquids exhibit instabilities that result in formation of cells and dendrites.
Mullins and Sekerka wrote a form of the equation 10.77 for low Peclet
number liquids as follows:
R
D
T
o
ÿ
2k
l
G
l
k
l
k
s
H R
k
l
k
s
ÿ
kÿR
2
D
2
0 10:78
and if is equated to the tip radius of a perturbation and, as assumed by Langer
and Muller -Krumbharr, that the marginal stability criterion allows the
calculation of the tip radius, it can be found that the tip radius in all cases is
426 Fundamentals of metallurgy

very small (larger than a critical radius), thus in diffusional growth situation we
are most often looking at dendrite growth and models of growth are very similar
to the heat transfer solutions where the transient solution of the mass transfer
equation will have the following form for a growing spher e from its own vapor :
R
dR
p
dt
D M
wtA
C
1
ÿ C
s
1
R
p
1
Dt
p
10:79
which at longer times gives the steady state solution:
R
dR
p
dt
D M
wtA
r
p
C
1
ÿ C
s
10:80
In the case of solidification of an alloy, if we assume that equation 10.75
describes the steady flux balance at the interface and assuming that we can
ignore the term for diffusion in the solid:
ÿD
l
dC
l
dr
xx
i
RC
1
l
ÿ C
i
s
RC
i
l
1 ÿ k
eq
10:81
and
R
D
r
C
i
l
ÿ C
1
1 ÿ k
eq
C
i
l
10:82
In a manner similar to that for solidification due to heat transfer we can write the
relation for the growth a cell as a hemispherical cap as follows:
Pe
c
c
1 ÿ
r
c
r
10:83
where Pe
c
is the comp ositional Peclet number (rR=2D) and
c
is the
dimensionless supersaturation:
C
i
l
ÿ C
1
1 ÿ k
eq
C
i
l
In a similar manner Ivantsov's solution can be used to describe the diffusion at
the tip of a paraboloid of revolution, where:
IPe
c
c
1 ÿ
r
c
r
10:84
and
IP Pe
c
expPe
c
E
1
Pe
c
E
1
Pe
c
ÿ0:577 ÿ lnPe
c
4Pe
c
Pe
c
4
Steady solutions are appropriate in many mass transfer situations as the
characteristic time to achieve equilibrium at the interface () is r
2
p
=D and, for
small radii, the characteristic time is small enough to be ignored.
Solidification and steel casting 427
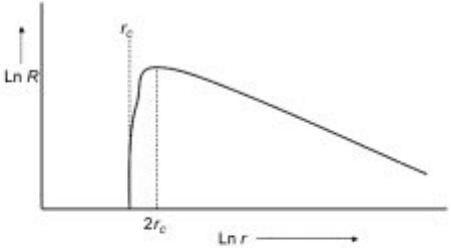
Equation 10.84 is schematically shown in Fig. 10.17 where the growth rate
exhibits a maximum.
10.4 The casting of steels
There are two main industrial methods for steel casting: ingot casting and
continuous casting.
15
Ingot casting is current ly only used in foundries and in
special products casting while continuous casting accounts for the majority of
the steel cast in the world. There are two major types of continuous casting
machines in which either the mold oscillates and there is a liquid oxide layer
between the mold and the steel shell, or the mold rotates and there is direct
contact between the mold and the shell of the casting.
In the casting of steels there are a number of initial solidification related
issues:
· Solidification can be initiated heterogeneously, by the oxides and nitrides that
are precipitated in the liquid steel during processing.
· In oscillation mold casters, the liquid oxide layer between the oscillating
mold and the shell is a potential glass former and thus tends to become a
mixture of crystallized solid and glass as it is cooled.
· The surface of cast steels in oscillating mold casters contains `oscillation
marks' that are related to the mold oscillation cycle itself.
· In the rotating mold or in ingot casting there can be an interaction between
the steel grade and the mold surface that can affect the solidification structure
at the surface of the casting.
10.4.1 The precipitation of oxides
Liquid steels at high temperatures always contain soluble oxygen and it is
normal practice to control the level of soluble oxygen by adding deoxidizers.
10.17 Schematic of growth rate verses radius for diffusion controlled growth of
a parabaloid.
428 Fundamentals of metallurgy
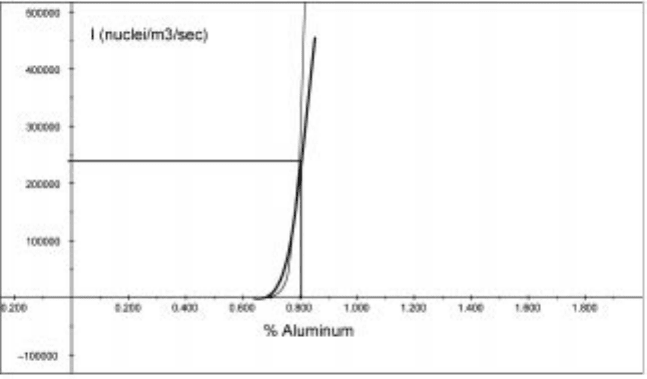
Aluminum is the most common deoxi dizer addition to liquid steels and solid
alumina forms by reaction with the aluminum and oxygen that are dissolved in
liquid steel. An example of the homogeneous nucleation rate at constant
dissolved oxygen content (0.008%) and as a function of aluminum content is
given in Fig. 10.18, where equation 10.27 was used to calculate the nucleation
rate. Use of equation 10.6 gives a critical ra dius of 9 angstroms fo r
homogeneous nucleation of alumina. This calculation is dependent on the
initially assumed conditions, for example, a starting oxygen content of 0.008%
was used; however, this data indicates significant supersaturation is necessary
before there is a significant nucleation rate for alumina precipitation. Once
nucleated, growth occurs rapidly to eliminate the supersaturation of aluminum
and oxygen in the liquid. For conditions in liquid iron where there is significant
liquid stirring due to natural convection or gas injection spheres of alumina can
grow to micron sizes in minutes; however, as seen in Fig. 10.19, at high growth
rates, alumina dendrites are commonly seen. The situation is more comple x than
it first appears, as at liquid steel temperatures alumina particles can easily
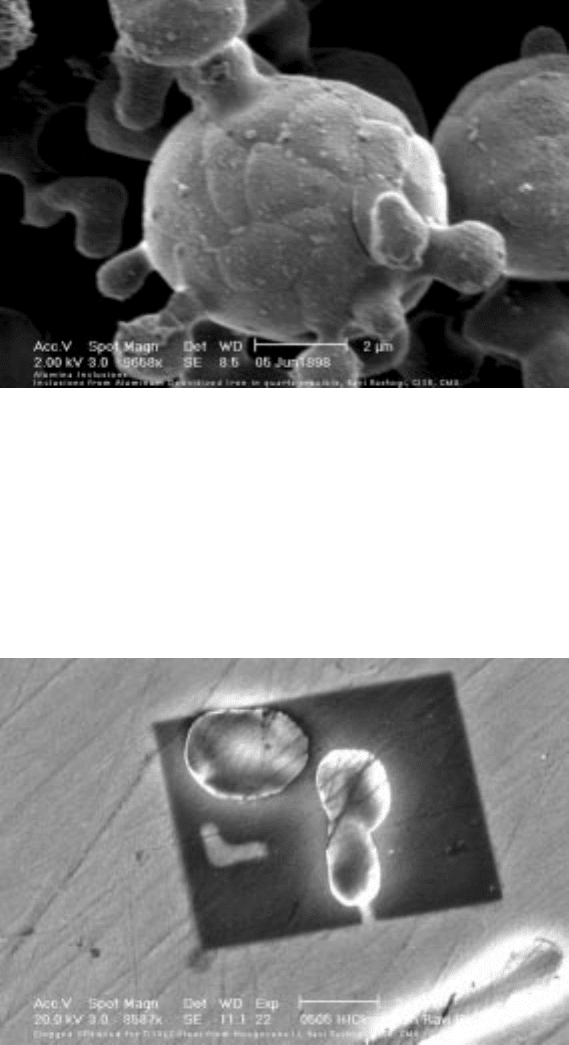
agglomerate, sinter and also coarsen. In Fig. 10.20, an equiaxed dendrite of
alumina can be easily seen. Both primary and secondary arms are clearly seen
radiating from a central position; however, close inspection indicates that
secondary arms are spheroidizing, causing necks in the secondary arms and
eventually disconnecting from the primary arm. This is the effect of
minimization of surface energy that causes the dendritic array to coarsen and
degrade to spheres and rods rather than the extended dendritic array.
18±20
Thus in the observation of alumina inclusions one must understand the
thermal history of the inclusion to fully appreciate the structure that is observed.
10.18 Nucleation rate for alumina formation in liquid iron.
Solidification and steel casting 429

For example fully spheroidized alumina inclusi ons can be found at low growth
rates as shown in Fig. 10.20.
There are many other deoxidation techniques and it is possible to form a
variety of inclusions chemistries in liquid steel. In titanium treated steels,
titanium nitride precipitates during cooling and alumina is a heterogeneous
nucleation site for titanium nitride. Thus it is common in titanium treated steels
10.19 Morphology of alumina in a deoxidation experiment.
18
Photograph by
R. Rastogi.
10.20 An equiaxed alumina dendrite exhibiting coarsening.
18
Photograph by
R. Rastogi.
430 Fundamentals of metallurgy
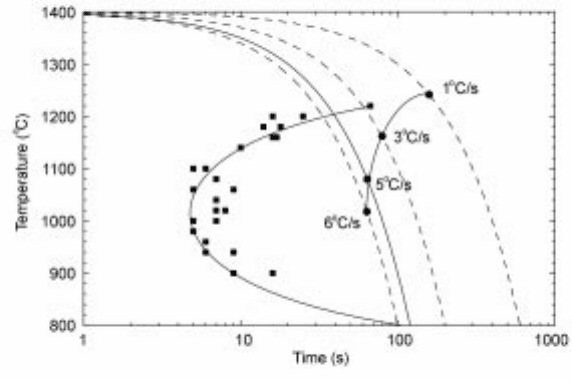
to find alumina particles that are completely surrounded by titanium nitride. An
example is shown in Fig. 10.21 for a titanium stabilized ultra low carbon steel
where the cubic titanium nitride surrounds the alumina.
The precipitation o f one inclusion on a pre-existing inclusion in liquid steels
is not unusual and manganese sulfide commonly precipitates on alumina during
solidification, for example. The inclusions precipitated in liquid steel are also
heterogeneous nucleat ing agents for solidification. This has be en well
10.21 Spheroidized alumina particle.
19
Photograph by R. Rastogi.
10.22 Titanium nitride particles in solid steel.
19
Photograph by R. Rastogi.
Solidification and steel casting 431
recognized in the welding literature and is only recently becoming interesting to
the bulk casting world where fully equiaxed continuous castings are now
possible in stainless steel grades where titan ium is the primary deoxidant and
titanium nitride can be precipitated before solidification (Fig. 10.22). This area
termed `oxide metallurgy' by Nippon Steel and is now an area of research focus
in addition to nucleation of solidification structures, transformation structures
also nucleate from the various inclusions that precipitate during casting and heat
treatment.
10.4.2 The solidification of mold slags
Mold slags are multicomponent oxides that are based on the calcium silicate
system where there are additions of soda, boria, alumina, magnesia and Lithia, in
addition to small amounts of calcium fluoride. These oxides, although brig ht at
steelmaking temperatures, are optically transparent as long as FeO and MnO and
titania levels are strictly controlled. This leads to the development of the single
and double hot thermocouple techniques that allowed the solidification behavior
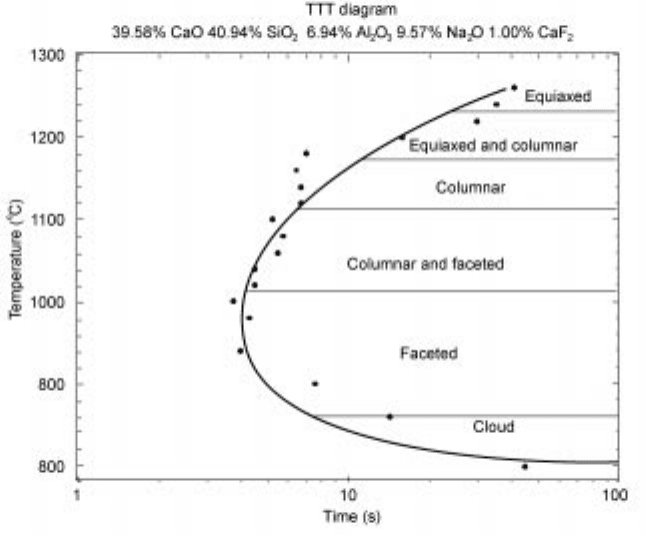
of slags to be fully understood. For example, from the wor k of Kashiwaya et
al.
21,22
and Orrling et al.,
23±27
both the TTT and CCT curve of a mold slag was
determined and is shown in Fig. 10.23.
27
From Fig. 10.23 we can see the typical C shape of the TTT curve and the fact
that from continuous cooling experiments the time to solidification start is
extended. Both curves are for the first observation of solid. As the liquidus of
this slag is approximately 1260ëC it is relatively easy to undercool these slags by
more than 300ëC in TTT mode. The criterion for glass formation in these
10.23 The TTT and CCT curve of an industrial mold slag.
27
432 Fundamentals of metallurgy
experiments is that the cooling rate should be greater than 6ëC per second and at
thermal gradients above this crystallization can be completely avoided. In these
thermocouple techniques solidification at higher temperatures always occurs on
the thermocoupl es as the platinum/rhodium of the thermocouple wire is a
heterogeneous nucleation point for solidification of the oxide; however, as the
temperature decreases the effect of the thermocouple as a nucleating agent
diminishes until eventually there is no effect and solid is seen to precipitate and
grow within the bulk of the liquid.
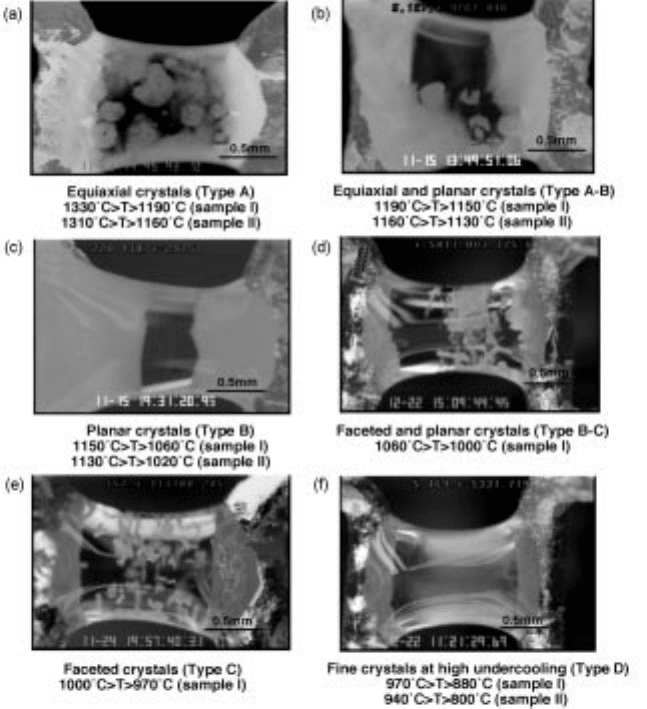
Orrling noted that the morphology of the solidification process is determined
by the details of the solidification path (Fig. 10.24) and in the measurement of
TTT diagrams using the DHTT made the map shown in Fig. 10.25.
10.24 Examples of the different solidification structures during construction of
a TTT curve.
27
Photograph by C. Orrling.
Solidification and steel casting 433
Orrling noted that at high temperature, slightly below the liquidus that
solidification initiated against the thermocouple itself; however, at temperatures
above 1200ëC the system was physically stirred due to slight variations in
temperature. The fluid flow resulted in the nucleated particles eventually being
removed from the thermocouple surface where they would continue to grow in
the undercooled liquid as equiaxed crystals. In addition, Orrling noted that the
equiaxed crystals as they grew were not stable and frequently broke apart due to
the local fluid flow conditions (see Fig. 10.26). These dendrite fragments would
then subsequently grow. The structure was then completely equiaxed.
As the temperature was decreased, the amount of observable stirring in the
system decreased due to the increasing viscosity of the liquid and eventually the
crystals did not detach from the thermocouples and complete columnar growth
was observed where both fronts would grow from each thermocouple and meet
in the middle (Fig. 10.24c). Of course, at intermediate temperatures, where
stirring was still observable, a columnar zone with an equiaxed zone between
both fronts was n oted. This was due to dendritic fragmentation as noted above.
As the temperature was further decreased, an area of very small faceted
crystals appeared between the two growing columnar zones (Fig. 10.24d) and, as
10.25 Map of solidification structures observed during the construction of a
TTT diagram.
27
434 Fundamentals of metallurgy
the temperature was further decreased, the extent of the faceted crystals
increased until at temperatures below 1000ëC only faceted crystals were
observed (Fig. 10.24e) and no precipitation on the thermocouples could be
discerned.
As the temperature was further decreased the crystals became very fine and
the density of crystals increased until it appeared `cloud-like' (Fig . 10.24f). This
occurred at 400ëC undercooling. This type of map was typical of all oxides
studied and indicated the strong effect of fluid flow on structure and also of
growth kinetics on structure as growth was always controlled by diffusion and
thus decreased with decreasing temperature. In addition, the mode of nucleation
changed from nucleation against the thermocouple to nucleation with the body
of the liquid. X-ray analysis suggested the composition of the crystal formed in
this slag was larnite (-Ca
2
SO
4
).
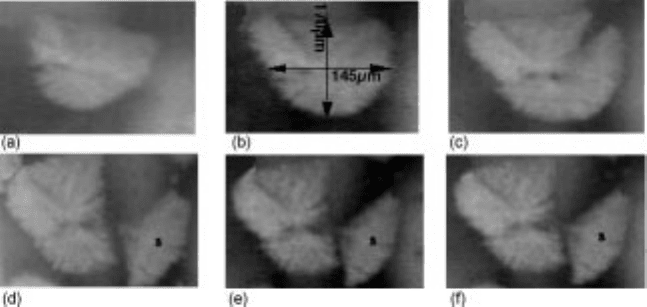
Growth rates in these studies were always linear, as shown in Fig. 10.27, and
suggested that the steady state approximation is appropriate and the diffusivi ty is
controlling growth rates where growth rates as a function of tip radius fits
Ivantsov's solution (equation 10.84).
The precipitation of multiple phases is also observed in the solidification of
mold slags. For example, from the first ever example of a TTT of a mold slag by
Kashiwaya et al.
22
two different crystal chemistries were determined by X-ray
diffraction. The presence of a defined crystal chemistry was determined solely
by the temperature of the isothermal hold during construction of a TTT curve
(Fig. 10.28) where dicalcium silicate (Ca
2
SiO
4
) was found at temperatures
above 1040ëC and cuspidine (Ca
4
Si
2
O
7
F
2
) at temperatures below 1040ëC. In this
situation dicalcium silicate will transform to cuspidine, if held at temperatures
below 1040ëC and diffusion rates are reasonable. The mold slag measured in this
study contained 7.6% Na
2
O and 6.5% Al
2
O
3
. As both elements do not appear in
10.26 Dendrite fragmentation at 1220 ëC due to fluid flow.
25
Photograph by C.
Orrling.
Solidification and steel casting 435
