Seetharaman S. Fundamentals of metallurgy
Подождите немного. Документ загружается.


pressure inside the droplet. This change in pressure is described by the Young±
Laplace equation which can be written for a sphere as:
P P
in
ÿ P
out
1
r
1
1
r
2
2
r
10:12
dP d 10:13
where is curvature and assuming that is a constant.
In general:
dG VdP ÿ SdT 10:14
thus, assuming that the total pressure is not affected by the formation of a
droplet, it is easy to show that the change in the equilibrium temperature due to
radius for a sphere is:
T
r
VT
M
H
lÿg
ÿ
2ÿ
r
10:15
S T
2V
r
10:16
and ÿ is the Gibbs±Thompson coefficient and equals V =S
lÿg
. Equation 10.16
is often called the Thompson±Gibbs relation. Thus, the equilibrium condensa-
tion temperature for a droplet decreases with decreasing radius. In fact, thi s is a
general finding. When one nucleates small droplets or particles, the equilibrium
phase diagram will change and the equilibrium position for the reaction will
always occur at a lower temperature than that given in a phase diagram that was
determined from bulk samples. Of course, this means that undercooling is
necessary for the formation of droplets and particles from a vapor or a liquid. A
similar equation can be developed for the effect of radius on equilibrium partial
pressure. This equation is generally referred to as the Kelvin equation:
RT ln
P
P
0
V
2
r
p ÿ p
0
2V
r
10:17
and relates the equilibrium partial pressure of a droplet (P
0
) to its size. Equation
10.17 indicates that as radius decreases, the equilibrium partial pressure must
increase. In equation 10.17, P
0
is the equilibrium partial pressure for a flat
interface. The similarities between equations 10.16 and 10.17 indicate different
manners by which the chemical potential can be derived. If the liquid is wetting
to the solid, Kelvin also showed that in capillaries:
RT ln
P
00
P
0
ÿ
2V
r
10:18
the equilibrium partial pressure for condensation will be less in a capillary than
on a flat surface, again indicating why concavities can be better sites for the
onset of nucleation.
406 Fundamentals of metallurgy

Equation 10.16, Kelvin's equation, also indicates an unstable equilibrium
position, if one considers the result of small fluctuations in radius for a
droplet in equilibrium with its surroundings. First, assume that one has a
population of mono-sized droplets in equilibrium with the vapor phase. If the
droplet spontaneously becomes larger by condensation, the new equilibrium
partial pressure for the new larger droplet size will be lower than the pressure
that previously was in equilibrium with the smaller droplet. The new larger
droplet is now in a situation where the actual pressure of the vapor from
which the droplet condensed is now above its new equilibrium partial
pressure. This condition will cause the droplet to further grow to reduce its
local pressure to the equilibrium pressure corresponding to its size. This
process will continue and the droplet will grow. Similarly, if a droplet
decreases due to evaporation, the new equilibrium partial pressure necessary
for the droplet will now be higher than the actual pressure and the droplet
will continue to evaporate. Obviously, there must be mass balance as the total
mass of droplets will not change, thus some droplets will grow and others will
decrease. Of course, these changes in local equilibrium will lead to gradients
in chemical potential between droplets and the driving force for mass transfer
between the droplets. In materials science, this phenomenon is known as
Ostwald ripening, and the coarsening of structures is also very common in
solidification as the system reduces its total surface area and moves to its
lowest energy state by reduction of surface area.
Thompson derived the effect of temperature on precipitation of droplets as a
function of radi us, where the effect of radius was to reduce the equilibrium
temperature for the transformation in the following manner:
ln
T
T
o
ÿ
2V
n
H
vap
r
10:19
showing the n ecessity for undercooling. In the derivation of Thompson's
equation, it is assumed that S H=T ; if, however, S H=T
M
, is
assumed, equation 10.15 results which is a clearer derivation and is preferred.
Gibbs' approach to nucleation and the Kelvin equation are yielding results
that are similar in that an unstable position occurs during nucleation. These two
views can be easily reconciled by considering the precipitation of droplets using
the natural variables of volume, pressure, area and number of moles. Thus
rewriting our thermodynamic equations for nucl eation in terms of the Helmholtz
free energy (F) where:
dF ÿPdV ÿ SdT dA
i
dn
i
10:20
it can be shown that at low values of supersaturation, that:
F 4 r
2
ÿ
4r
3
3V
n
RT ln
P
0
P
0
10:21
Solidification and steel casting 407
If the maximum of this function is found (dF=dr 0), Kelvin's equation results.
Of course, the maximum must occur at r
and thus Kelvin's equation is satisfied
for droplets of a critical radius. Using Kelvin's equation, it is possible to
calculate the size of a critical radius for droplet formation. For example, at 0ëC
and at a supersatuation of 4.2, water droplets are observed in water vapor. This
leads to a calculation of r
of 0.8 nanometers which is a cluster of approximately
70 water molecules. For solidification of a solid phase one must change the
various constants to those of the solid. For exam ple, equation 10.16 would be
written with the solid±liquid interfacial tension and the entropy change for
solidification.
This discussion of droplets leads to some interesting issues in solidification:
1. The formation of very small particles necessitates that surface energy must
be included in our description of equilibrium. Thus, current equilibrium
phase diagrams cannot predict the onset of solidification as they are based
upon bulk observations or calculations using bulk properties. Thu s
equilibrium phase diagrams as a function of particle size are necessary
and a diagram of this type was recently calculated by Tanaka et al.
13
for the
system copper±lead. Similar affects of particle size have been measured by
Sambles
14
who noted that the melting temperature of pure gold decreased
markedly (by more than 100K) when the particle size decreased below 20
nanometers.
2. Solidification structures will naturally coarsen due to the influence of
curvature on local equilibrium.
The discussion of the thermodynamics of solidification so far has lead us to
understand that the equilibrium phase diagram does not neces sarily help us in
our understanding of the initiation of solidification and that, when solidification
occurs by fluctuations of small groups of atoms or molecules, the phase diagram
must be altered due to the affect of radius on the equilibrium position.
10.2.4 Nucleation rate and the formation of non-equilibrium
solids
In addition to the effect of radius, one must also include the effect of cooling rate
when discussing solidification, as it is possible to undercool liquids to the point
that the liquid be gins to exhibit solid-like b eha vior. For example, the
undercooled liquid can fail in a brittle mode at low temperatures or deform
plastically at higher temperatures. Thus, not only can the phase diagram be
changed by particle size, it should also take into account the effect of cooling
rate on the potential for metastable phase formation and glass formation. Clearly
this is beyond the realm of thermodynamics alone.
Following the view that small fluctuations are responsible for the initiation of
solidification,
11,12
it was postulated that the homogeneous nucleation rate (J)
408 Fundamentals of metallurgy

should be proportional to the number of critical size nuclei (n
c
), that is a nuclei
with a radius r
, where:
J / n
c
10:22
and that the number of these nuclei would follow the Frenkel size distribution
equation (10.23), where one assumes that the entropy change of the solid±liquid
system must be included by calculating the free energy of mixing of embryos
(potential nuclei) with the liquid atoms (n
l
) by assuming an ideal mixing model:
n
c
n
l
exp
ÿG
c
k
b
T
10:23
If the clusters evolve by a bimolecular reaction with forward and reverse rates of
monomer addition where critical size nuclei grow by addition of atoms at the
interface, an expression for the steady state nucleation rate can be derived
assuming an activated process:
J N
s
n
c
10:24
J N
s
kT
h
exp
ÿG
d
k
b
T
n
l
exp
ÿG
c
k
b
T
10:25
where N
s
is the number of atoms adjacent to the interface and in a position where
a potentially successful jump is possible and is the jump frequency of an atom
from the liquid to the solid, G
d
is the activation energy at the solid±liquid
interface for a successful jump of an atom in the liquid to the surface of the
nuclei and h is Planck's constant. G
d
is the kinetic barrier to nucleation and
G
c
is the therm odynamic barrier to nucleation. This can also be written (from
equations 10.5 and 10.7) as:
J N
s
kT
h
exp
ÿG
d
k
b
T
n
l
exp ÿ
16
3kT
3
T
2
M
H
2
v;s!l
T
2
!
10:26
J N
s
kT
h
exp
ÿG
d
k
b
T
n
l
exp ÿ
16
3kT
3
RT ln S
2
!
10:27
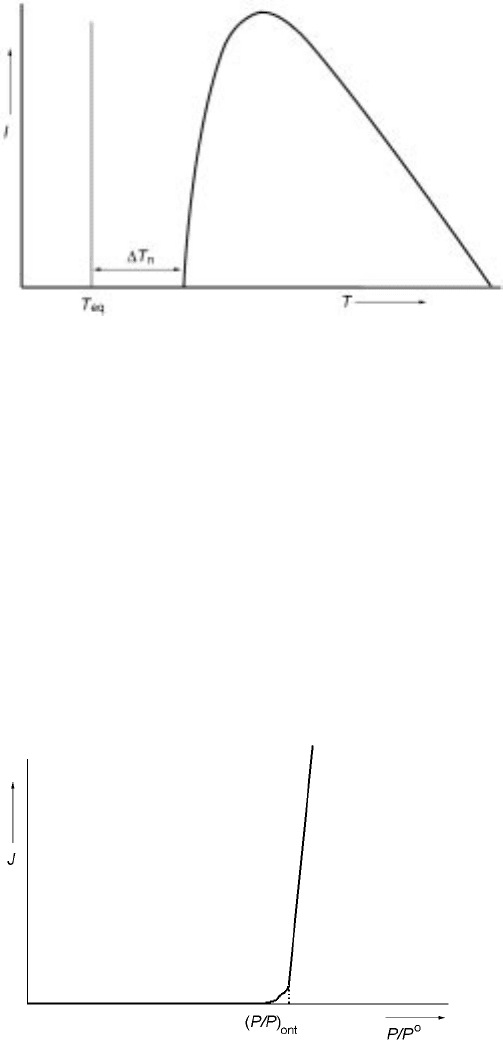
Equation 10.26 is plotted schematically in Fig. 10.5 where the nucleation rate
goes through a maximum as temperature decreases. T
n
in Fig. 10.5 is the
undercooling necessary for an observable nucleation rate of 1 nuclei per cm
3
per
second. In metals it is very difficult to actually measure the maximum in Fig.
10.5 due to difficulties in accessing extreme undercool ings; however, such
results are often seen in liquid oxides and in polymers.
Equation 10.27 is plotted schematically in Fig. 10.6, where in this case, the
nucleation rate continues to increase with increasing supersaturation.
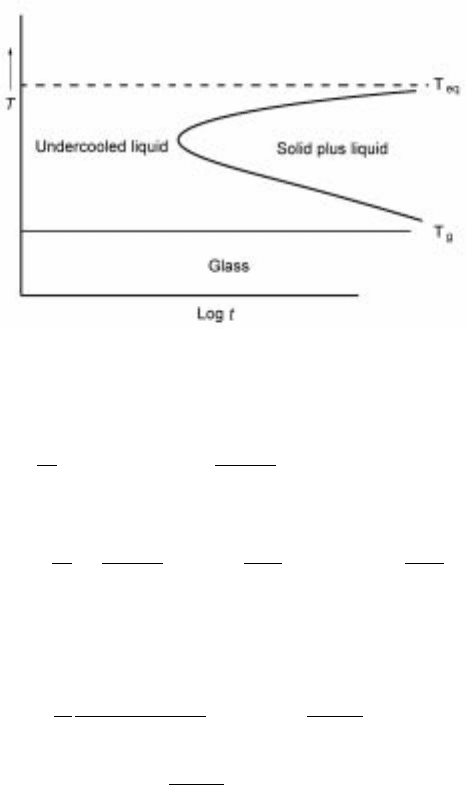
The time to nucleate is proportional to the reciprocal of the nucleation rate.
Thus time±temperature±transformation (TTT) curves can be derived from the
Solidification and steel casting 409
nucleation rate and such a curve is shown schematically in Fig. 10.7. In this
figure the dashed line indicates the position of the first observable solid in an
experiment.
Other curves could also be drawn to denote the fraction of solidification and
to indicate the progression of solidification with time. In Fig. 10.7 the equili-
brium position of the phase transformation is noted, as is the glass transition
temperature. Thus this figure schematically shows the position of the possible
phases and indicates the stability regimes (with temperature and time) of the
liquid, the glass and the area where the solid crystallizes from the liquid.
Theoretically all liquids should be able to be formed at high cooling rates;
however, the realm of achievable cooling rate is well defined and only those
liquids that can be cooled quickly enough to avoid solid precipitation can be
made as glasses.
10.5 Nucleation rate (J) as a function of temperature.
10.6 The effect of supersaturation on the nucleation rate.
410 Fundamentals of metallurgy
Alternatively,
1,8
if the jump frequency is calculated from:
D
l
a
2
and N
s
4r
2
a
2
10:28
then, for typical metals, where J is measured per cm
3
per second:
J
D
l
a
2
4r
2
a
2
!
n
l
exp
G
kT
10
34
exp
G
kT
10:29
The above discussion of nucleation rate concerns homogeneous nucleation, if
one takes into account the fact that a heterogeneous nucleation site exists, then
equation 10.29 can be rewritten as:
J
het
D
a
2
2r
2
cr
1 ÿ cos
a
2
n
a
exp ÿ
G
hom
k
b
T
f
10
24
exp ÿ
G
hom
k
b
T
f
10:30
where n
a
is the number of atoms in contact with the surface of potential
nucleating sites (approximately taken as 10
24
in this cal culation
5
). Of course,
this means that J / N
a
where N
a
is the area of the nucleant and related to the
number and size of the nucleating particles.
From equation 10.30 , heterogeneous nucleation is promoted by:
· A stable solid material that exists in the liquid above the solidification
temperature. This solid can be physically added and mixed or precipitated
from solution during cooling.
· A low contact angle between the precipitated solid and the heterogeneous
nucleating surface.
10.7 Schematic TTT curve.
Solidification and steel casting 411
·
A large surface area of the potential nucleant.
The contact angle between solids in a liquid is not a readily measurable contact
angle in non-transpar ent liquids. In addition liquid±solid interfacial ener gies are
not easily determined, thus the use of Young's relation (equation 10.8) to
determine nucleating species is not particularly useful. Thus other criteria are
necessary to allow the identification of potential nucleating species.
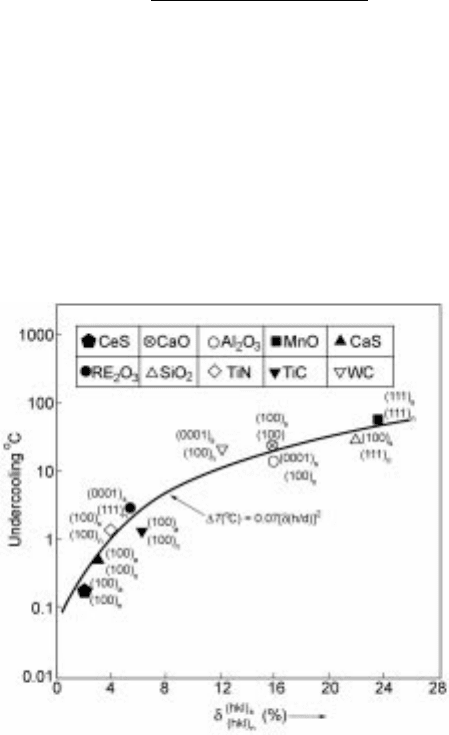
Knowledge of surface structure is useful in the determination of potential
nucleants. If one assumes that epitaxy is important then nucleation should occur
on planes that have a low misfit or disregistry with the plane to be precipitated.
Bramfit calculated the disregistry () as follows:
X
3
i1
hkl
n
hkl
s
jduvw
i
n
cos ÿ duvw
i
s
j
duvw
i
n
" #
100% 10:31
where (hkl)
s
and (hkl)
n
are low-index planes in the solid and nucleant, [uvw ]
s
and
[uvw]
n
are low-index directions in the (hkl)
s
and (hkl)
n
planes respectively,
d[uvw] is the spacing along [uvw], is the angle between [uvw]
s
and [uvw]
n
and
i is one of the three directions of the crystal with minimum index. Bramfit
15
used
this parameter to explain the difference in efficiency of heterogeneous nucleants
of ferrite by measuring the degree of undercooling during solidification as
shown in Fig. 10.8.
Of course, measurement of the undercooling for initiation of solidification is
the most accurate assessment of the effectiveness of a nucleant.
10.8 Effect of lattice disregistry on undercooling.
16
412 Fundamentals of metallurgy

10.3 The growth of solids
In the discussion of growth rates there are a number of issues. The first is, what
is controlling the growth rate? There are three potential general answers:
interface kinetics, mass transfer or heat transfer; however, mixed results are also
possible. In addition there are two major types of interface: flat and diffuse. If
the interface is diffuse as in most metals, growth will be continuous, while if the
interface is flat as in oxides, for example, the interface will grow laterally and
the interface will be faceted. The entropy of fusion is often used to determine
which type of interface will predominate and if S=R < 2; the interface
will be diffuse.
10.3.1 Interface dominated growth rates
Once nucleated, particles must grow and although the nucleation process is
outside of our abilities to observe in liquids, one can certainly observe the
growth stage after nucleation. In the above discussion of nucleation, it was
assumed that growth was in an undercooled liquid and atom attachment to an
interface controlled the growth rate and the jump frequency at the interface was
very important. If one follows this viewpoint and assumes that growth is an
activated process, then the Wilson±Frenkel relation results:
R
D
a
1 ÿ exp
G
crystallization
k
b
T
D
a
1 ÿ exp
H
crystallization
T
k
b
TT
m
10:32
and, if diffusivity is related to viscosity via the Stokes±Einstein relation, it
follows that:
R
k
b
T
3a
2
1 ÿ exp
H
crystallization
T
k
b
TT
m
10:33
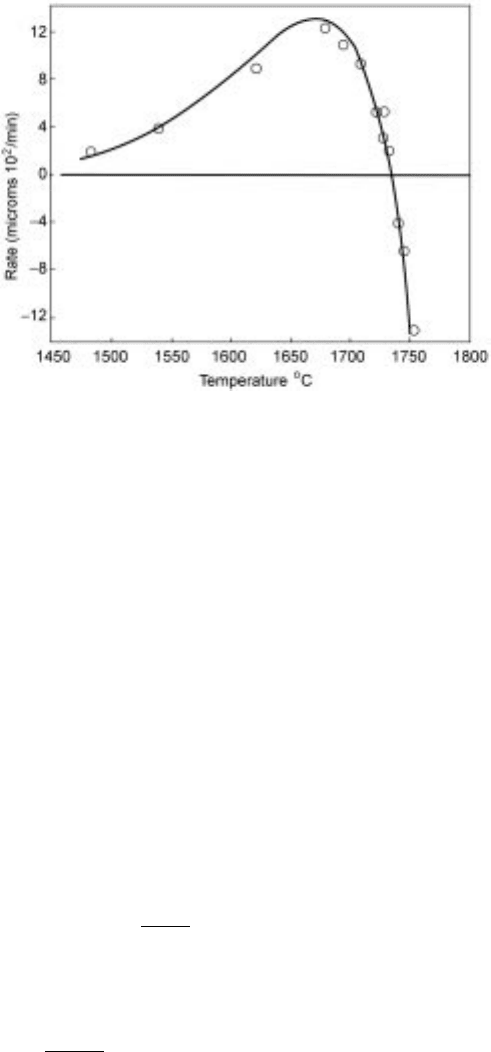
This relation can be used to predict the growth rate as a function of temperature
for crystobollite precipitation from fused silica, as shown in Fig. 10.9.
If one assumes that not all sites on a surface are appropriate and that a
successful jump occurs only in specific positions, then a correction factor f can
be attached to equation 10.33 and for a growing monolayer, if f T=2T
M
:
R
T k
b
T
6
2
T
M
a
2
1 ÿ exp
H
crystallization
T
k
b
TT
m
10:34
If equations 10.33 and 10.34 are approximated by the following approximation,
if 1 ÿ expÿx x, then equation 10.33 indicates that:
R / T 10:35
and equation 10.35 indicates that:
R / T
2
10:36
Solidification and steel casting 413
If one assumes that growth is by a screw dislocation emerging at a surface , a
similar relation to equation 10.36 is found. In metals the undercoolings
associated with surface growth mechanisms are very small and only at high
growth rates do interface kinetics become an issue.
As already noted the growth phase of solidification is easily observed and if
one assumes that there is a steady state nucleation rate, that the growth rate is
constant and the liquid is consumed by the growth of the particles, the following
general Kolgmogorov, Johnson, Mehl, Avrami (KJMA) equation can be
developed:
5
X
t
1 ÿexp ÿc
g
Z
t
0
J
t
Z
t
0
G
t
dt
d
dt
" #
10:37
where X
t
is the fraction transformed, c
g
is a shape factor, J
t
is the nucleation rate,
G
t
is the growth rate and d represents the dimensionality of growth.
For example, if we had growth of a sphere at constant growth rate and a
constant nucleation rate (J
v
), then as c
g
is 4=3, d 3, and G
t
is a constant, the
Johnson±Mehl equation results:
1 ÿ X
t
exp ÿ
J
v
R
3
3
t
4
10:38
From this equat ion, if J
v
and R are kn own as a function of temperature and we
assume small values of X
t
, it follows that:
X
t
J
v
R
3
3
t
4
10:39
10.9 The growth or melting rate of crystobollite as a function of temperature.
6
414 Fundamentals of metallurgy
If the limit of observation for X
t
is assumed to be 10
ÿ6
the time when the first
observation of solidi fication at a given temperature T could be calculated from a
knowledge of J
v
and R. Fo r exam ple, using equations 10.29 and 10.32, for
homogeneous nucleation followed by growth by the monolayer model, the TTT
curve could be calculated.
Although the above growth models seem reasonable in pure liquid oxides
where undercooling is easy and heat transfer is not an issue; however, in metals
with a high latent heat of solidification or during highly exothermi c reactions,
heat transfer tends to control the growth rate after the initial formation of solid.
In multicomponent solutions mass transfer in the liquid can become rate
controlling rather than atom attachment.
10.3.2 Heat transfer dominated growth rates
In heat transfer dominated solidification, the rate of solidification is determined
solely by the ability to transfer heat away from the interface. In undercooled
liquids heat can be transferred either to the liquid or into the growing shell. The
amount of solidification is thus related to the heat flux removed from the
interface. If the amount of heat released during solidification is measured per
unit mass and the thermal gradient in the solid (dT=dx) is G
s
and the thermal
gradient in the liquid is G
l
, then the interface heat balance for a planar interface
is as follows:
k
s
G
s
ÿ k
l
G
l
H R 10:40
where is the density and k
s
and k
l
are the thermal conductivities of the solid
and liquid respectively. Thus the maximum growth rate occur s when G
l
is
negative (undercooled) and G
s
is positive (normal solidification). Th e relation
also shows that an interface can be stabilized (R 0) by ensuring that
k
s
G
s
k
l
G
l
. If convection heat transfer controls thermal transport in the liquid
then equation 10.40 would be rewri tten as follows:
k
s
G
s
ÿ h
l
T
b
ÿ T
t
H R 10:41
To avoid the necessity of solving for h
l
it is not uncommon in calculations to
substitute a fictitious effective conductivity in equation 10.40 to account for a
higher rate of heat transport than would be calculated from conduction heat transfer.
The first issue in any heat transfer problem in solidification is to define the
interface temperature, as it is that temperature that will define the temperature
that the heat must flow from. The starting point is, of course, the equilibrium
phase diagram and to calculate the interface temperature one must first take into
account the effect of chemistry (T
c
), and, if the interface has curvature, then
this undercooling must also be included (T
r
), such that:
T
int
T
Mpt
ÿ T
c
ÿ T
r
10:43
Solidification and steel casting 415
