Seetharaman S. Fundamentals of metallurgy
Подождите немного. Документ загружается.

them, slag and metal, which are always solutions, play essential roles in many of
extraction and refining processes. A design of a sub-proce ss, e.g. ladle treatment,
would demand a reliable thermodynamic descriptions of all the phases. Since
slags and liquid metals are solutions, their thermodynamic descriptions would
need mathematical models. Unfortunately, none of the existing thermodynamic
models is reliable for all slag systems. Even in the case of liquid metals, solution
models are usually only reliable in certain composition ranges. Hence, the
choice of models is always a compromising process. This process requires an in-
depth understanding of the models and experience. The present chapter does not
intend to make the choice for the readers. Instead, it will introduce briefly some
of the solution models, so that the readers are prepared for the later discussion.
Slag models
A number of slag models are available in the literature with varying degrees of
success. Th ey may be classified into two main groups, namely structural based
models
1±5
and empirical or semi-empirical models.
6±14
The latter type is the
most commonly used one. Since empirical and semi-empirical models are based
on experimental information, the quality of the experimental data has a strong
effect on the results of the model calculations.
Kapoor and Frohberg
6
developed a model, in which the structure of silica
melts are represented by symmetric and asymmetric cells composed of one
oxygen ion surrounded by two equal or two different cations. This model was
later extended to multicomponent systems by Gaye and Welfringer,
7
known as
the IRSID model. The IRSID model has been applied to a number of
multicomponent systems and good agreement between the results of model
calculation and experimental data has been reported.
7
The two-sublattic e model developed by Hillert et al.
8
for ionic solutions
assumes that one sublattice is occupied by cations and the other one by anions
and neutral species. Even in this model, complex anionic species are used.
8
It
should be mentioned that difficulties have been encountered in choosing the
suitable species in both the two-sublattice and the IRSID models.
9
The fractions
of different species optimized in this way are somewhat arbitrary, as very little
experimental evidence is obtained to support the same.
Pelton and Blander
10
developed a model based on the well known quasi-
chemical approach to describe the silicate systems. Difficulties arise when a
system contains a liquid phase exhibiting strong structural ordering at a certain
composition. By choosing the composition of orthosilicate as the maximum
ordered, they were able to describe a number of ternary silicate systems using
solely the information from the binary systems.
Temkin
11
developed a model for the ideal mixing of molten salts. For mixing
of two liquid salts AX and BY, where A and B are cations and X and Y are
anions, the idea l entropy of mixing may be expressed as:
376 Fundamentals of metallurgy

S
M
ÿRy
A
ln y
A
y
B
ln y
B
y
X
ln y
X
y
Y
ln y
Y
9:7
where y
A
, y
B
, y
X
, y
Y
are the ionic fractions of the ions A, B, X and Y. The
assumption that the mixing between the salts is ideal gives the expression for the
Gibbs energy of mixing:
G
M
ÿT S
M
9:8
The use of the regular solution model to describe the thermodynamics of silicate
melts was originally suggested by Lumsden.
12
A silicate melt is considered as a
matrix of oxygen ions, O
2ÿ
with different cations including Si
4+
distributed in it.
Ban-Ya and Shim
14
have successfully applied the regular solution approach to a
number of binary, ternary and quaternary silicate systems.
Combining the approaches of Temkin,
11
Lumsden
12
and Hillert,
8
a model for
ionic melts has been developed at KTH.
15,16
According to this model, an oxide
melt is considered to consist of a matrix of oxygen ions with various cations
distributed in it. In a system containing m different oxides, C1
c1
O
a1
, C2
c2
O
a2
, . . .
Ci
ci
O
ai
, . . . C
cm
O
am
, the cations and anions can be grouped into two separate
subgroupings:
C1
1
; C2
2
; . . . Ci
i
. . . Cm
m
p
O
2ÿ
q
9:9
where p and q are stoichiometric nu mbers, Ci
i
stands for cations, the superscript
represents the electrical charge. The thermodynamics of the melt is expressed by
the next-nearest-neighbour interactions, viz., the interactions between different
cations in the presence of O
2ÿ
. Consideration of the next-nearest-neighbour
interactions necessitates the use of the cation fractions defined as:
y
Ci
N
Ci
X
j1 to m
N
C
j
9:10
In equation 9.10, N
Ci
is the number of moles of cation Ci
i
and the summation
covers all the cations. If X
Ci
ci
O
ai
and G
o
Ci
ci
O
ai
represent the mole fraction and the
standard Gibbs energy of oxide Ci
ci
O
ai
, the integral Gibbs energy of a solution
can be expressed as:
G
m
X
X
Ci
ci
O
ai
G
o
Ci
ci
O
ai
RTp
X
y
Ci
ln y
Ci
G
E
9:11
G
E
, the excess Gibbs energy of the solution in equation 9.11 is described as:
G
E
f T; y
Si
4
X
i1 to mÿ1
X
ji1 to m
y
Ci
y
Cj
Ci;CjO
!
9:12
Ci;CjO
in the above equation represents the interaction between cations Ci and
Cj whe n O
2ÿ
ions are present. This interaction is a function of temperature and
composition. The presence of the function, f T; y
Si
4
in equation 9.12 is due to
Improving process design in steelmaking 377
the fact that the excess Gibbs energy is not zero as the composition approaching
pure SiO
2
when the hypothetical standard state for silica is adopted.
15,16
According to Temkin's theory,
11
the activity coefficient of Ci
ci
O
ai
, is related
to the activity coefficient of the corresponding cation, Ci
ci
, which, in turn, is
expressed by the partial excess Gibbs energy of the same species:
Ci
ci
O
ai
ci
Ci
ai
O
ci
Ci
exp
G
E
Ci
i
RT
9:13
As an example,
15
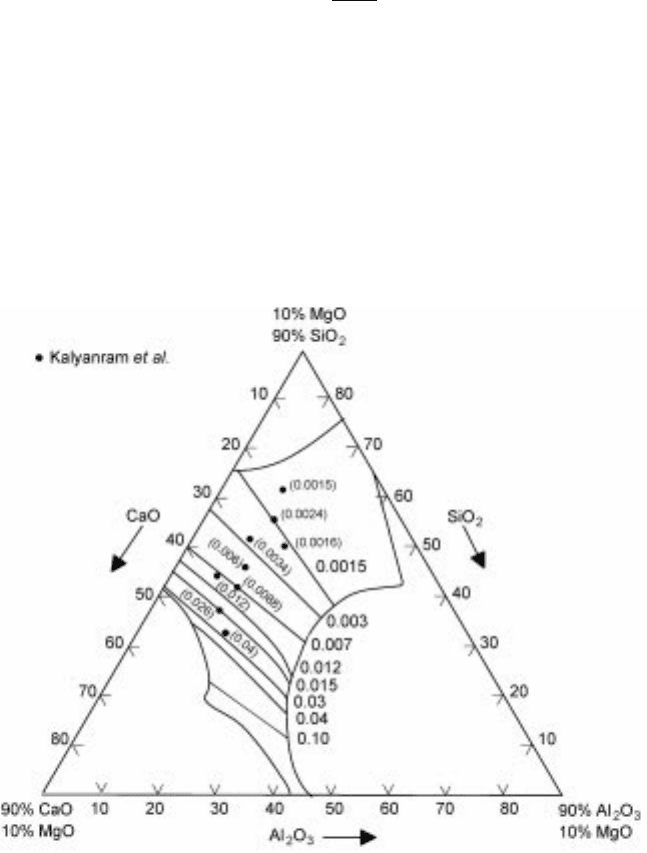
Fig. 9.3 presents the calculated CaO activit ies using this model
at constant MgO content (mass pct MgO 10) and at 1773K in the Al
2
O
3
-CaO-
MgO-SiO
2
system. The experimental data by Kalyanram et al.
17
are also
included for comparison. Considering the extremely low activity values, the
agreement between the values predicted by the model and the experimental
results can be considered reasonable.
The slag compositions in different industrial processes differ greatly. In Table
9.1, some typical slag compositions, relevant to the steel industry, used in the
blast furnace (BF), electric arc furnace (EAF) and ladle furnace (LF) are
presented. As an example of the model calculati ons, the effect of the
9.3 Calculated CaO activities at constant MgO content (mass pct MgO 10)
and at 1773K in the Al
2
O
3
-CaO-MgO-SiO
2
system.
378 Fundamentals of metallurgy
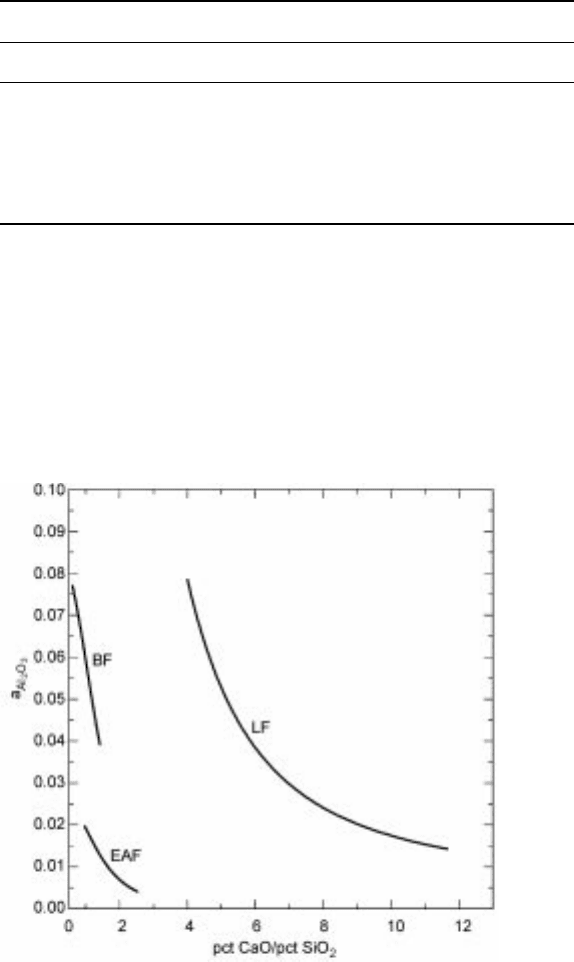
replacement of SiO
2
by CaO on the activities of alumina in the case of BF, EAF
and LF slags is illustrated in Fig. 9.4. In the calculation for each type of slag, the
contents of the other components given in Table 9.1 were kept constant. It is
seen in Fig. 9.4 that the activity of alumina is lower in the EAF slag than in the
BF slag at the same mas s pct CaO/mass pct SiO
2
ratio. It is also seen that an
increase of the mass pct CaO/mass pct SiO
2
ratio leads to a considerable
decrease of the alumina activity, irrespective of the type of the sla g. However,
the decrease in alumina activity with the increasing mass pct CaO/mass pct SiO
2
Table 9.1 Some typical slag compositions of the electric arc furnace (EAF),
blast furnace (BF), and ladle furnace (LF) processes
Compositions in mass pct
Oxide EAF BF LF
Al
2
O
3
10 13 33
CaO 40 32 54
FeO 15 2 0.5
MgO 9 17 7
MnO 5 2 0.5
SiO
2
21 34 5
9.4 The effect of the replacement of SiO
2
by CaO on the activities of alumina in
the case of BF, EAF and LF slags.
Improving process design in steelmaking 379

ratio is more profound in the case of BF and EAF slags. The substantial
variations of the oxide activities with slag composition again emphasizes the
importance of the thermodynamic consideration in the process design.
Solution models for liquid metal
A number of solution models are currently available. Wagner's model
18
is the
most commonly used one. For dilute solutions, the model descr ibes the activit y
coefficient
i
for a solute i by Taylor series,
ln
i
ln
o
i
X
N
j2
X
j
@ ln
j
@X
j
ln
o
i
X
N
j2
X
j
j
i
9:14
In this model, the derivatives higher than first order are not considered. The
reference state
o
i
is an infinitely dilute solution with respect to the solute i. The
use of only first order derivatives restricts the use of Wagner's equation to very
low concentrations of the solute concerned.
In practical application, it is usually preferable to use concentration of mass per
cent and the Henrian standard state. In this case, Wagner's equation is given by:
ln f
i
X
N
j2
% j
@ ln f
j
@% j
X
N
j2
% j e
j
i
9:15
The relationship between
j
i
and e
j
i
is
j
i
230e
j
i
M
j
M
solv
1 ÿ
M
j
M
solv
9:16
where M
j
and M
solv
are the atomic weight for component j and for the solvent.
To extend the model calculation to higher concentrations, second-order
interaction parameters have been adopted by Lupis and Elliot.
19
However, only
a limited number of interaction parameters higher than first order is available.
A number of models have been developed on the basis of Wagner's model.
For example, Pelton and Bale
20,21
have proposed the Unified Interaction
Parameter Model (UIPM) taking into consideration the influence of the solv ent.
Harja et al.
22
have modified Wagner's method for ternary systems by using
boundary conditions that apply to concentrated solutions. The same method has
later been adopted by Ma, Ohser and Janke,
23
but has been extended to a
multicomponent system. While these models have been found to have improved
performance in the case of concentrated solutions, the lack of the model
parameters has in many cases limited the use of these models.
Other types of solution mode ls are also available in the literature. Since the
present chapter is to introduce the use of the solution model in process design, it
is not going to list all the thermodynamic models. Interested readers may find
them in the literature.
18±27
380 Fundamentals of metallurgy
9.3.2 Mass balance constraints
Although in many processes, the system would not reach therm odynamic
equilibrium, a thorough thermodynamic evaluation is still necessary to examine
the limit of the reaction. In a heterogeneous process, equilibrium is usually
reached by the fluxes of the involved elements from one phase to another by
interface reactions. Hence, mass balance must be taken into account along with
the thermodynamic constraints to estimate the amounts of the raw materials
required and the final compositions of the phases participating the reaction(s).
We shall take desulphurization in the ladle treatment as an example to
illustrate this aspect. For the sake of clarity, we shall assume, at this p oint, that
the slag composition is constant. A detailed discussion taking all the parallel
reactions into consideration will be presented in the next section.
The desulphurization can be expressed by the equation:
S
metal
O
2ÿ
slag
O
metal
S
2ÿ
slag
9:17
The ability of a slag to take up sulphur from a metallic phase is often expressed
as sulphide capacity, C
S
, which is defined as:
28
C
S
mass%S
P
O
2
P
S
2
s
9:18
where P
O
2
and P
S
2
are the partial pressures of oxygen and sulphur gases
prevailing in the adjacent of the slag phase. In the case of slag±metal reaction,
P
O
2
and P
S
2
are related to the activities of oxygen and sulphur in the liquid metal
through the following reactions:
1
2
O
2
gas O
metal
9:19
1
2
S
2
gas S
metal
9:20
The sulphur partition ratio, L
S
is related to the sulphide capacity by the following
relationship:
L
S
mass%S
slag
mass%S
metal
C
S
f
S
K
19
a
O
K
20
9:21
where a
O
and f
S
are the activity of oxygen and activity coefficient of sulphur in
the liquid metal, respectively. K
19
and K
20
in equation 9.21 stand for the
equilibrium constants of reactio ns 9.19 and 9.20. The equilibrium constants K
19
and K
20
are well established for liquid iron and can be found in the literature.
29
If
the values of a
O
and f
S
are known, the partition of sulphur between the slag and
metal can be evaluated on the basis of the sulphide capacity of the slag using
equation 9.21. For simplicity, we could assume the slag composition as well as
a
O
and f
S
are constant. It should be pointed out that the composition of the slag,
a
O
and f
S
in the metal would vary. These variations will be considered in the
Improving process design in steelmaking 381

next section. Our task at this point is to estimate preliminarily the amount of slag
required to bring down the initial sulphur content in the liquid metal,
mass%S
metal;0
to the desired value, mass%S
metal;1
when the slag composition
is known.
Usually, the sla g having an initial sulphur concentration mass%S
slag;0
is not
in thermodynamic equilibrium with the metal with respect to sulphur. The
chemical potential difference will drive the flux of sulphur from metal to slag to
satisfy equation 9.21,
L
S
mass%S
slag;0
mass%S
slag
mass%S
metal;0
ÿ mass%S
metal
C
S
f
S
K
19
a
O
K
21
9:21
0
To maintain the mass balance, mass%S
slag
is related to mass%S
metal
by
the following equation:
mass%S
metal
W
metal
100
mass%S
slag
W
slag
100
9:22
where W
metal
and W
slag
are the weight of the liquid metal and the slag,
respectively. Using equat ions 9.21
0
and 9.22, one can estimate the value of W
slag
on the basis of the sulphide capacity, C
S
(assuming a
O
and f
S
are known).
In some cases, the industry would want to find a suitable slag composition
with a desired amount of slag. In such case, one can evaluate the sulphide
capacity using equations 9.21
0
and 9.22. The range of the slag composition can
be determined using the sulphide capacity models
30±32
on the basis of the
evaluated C
S
. In fact, it is very often a compromising procedure to determine the
amount and the composition of the slag in most of the practices.
9.3.3 Thermodynamics and mass balance in ladle treatment
In orde r t o further demonstrate the principle of the co nsidera tion of
thermodynamic constraints and mass balance in detail, we shall discuss this
aspect in the case of ladle treatment. In the previous section, the slag
composition was assumed constant. In a real industrial practice, slag
composition changes with time mostly because of the deoxidation and the
corrosion of the refractory lining. In addition to the variation of the slag
composition, the concentrations of the dissolved elements in the liquid metal
also vary with time. To account for the composition changes of both liquid metal
and slag, all the parallel chemical reactions should be considered
simultaneously. Let us take the deoxidation by aluminium addition as an
example to illustrate how mass balance should be considered. Ladle slag usually
contains Al
2
O
3
, CaO, FeO, MgO, MnO and SiO
2
. Since the solubilities of Mg
and Ca in the li quid iro n are very low,
33
their fluxes from one phase to another
would not affect the mass balance with respect to oxygen appreciably. Hence,
the following reactions should be considered in the design of a process.
382 Fundamentals of metallurgy

For Al
2
O
3
: 2[Al] 3[O] Al
2
O
3
(9.23)
For SiO
2
: [Si] 2[O] SiO
2
(9.24)
For MnO: [Mn] [O] MnO (9.25)
For FeO: [Fe] [O] FeO (9.26)
The addition of Al would not only change the concentration of aluminium in the
liquid metal and disturb the equilibrium of reaction 9.23, but als o disturb the
equilibriums of the reactions 9.24 to 9.26. To reach a new equilibrium between
the slag and metal, the fluxes of Al, Fe, Mn, Si and O are generated. These
fluxes would result in the concentration changes, X
Al
2
O
3
, X
FeO
, X
MnO
and
X
SiO
2
in the slag as well as concentration changes, mass%Al, mass%Fe,
mass%Mn, mass%Si, and mass%O in the liquid metal. To maintain
t he mass balance and the thermodynamic equilibrium, the following
relationships must be kept.
K
Al
2
O
3
Al
2
O
3
0
X
Al
2
O
3
X
Al
2
O
3
f
2
Al
0
mass%Al ÿ mass%Al
2
f
3
O
0
mass%O ÿ mass%O
3
9:27
K
FeO
FeO
0
X
FeO
X
FeO
f
Fe
0
mass%Fe ÿ mass %Fe f
O
0
mass%O ÿ mass%O
9:28
K
MnO
MnO
0
X
MnO
X
MnO
f
Mn
0
mass%Mn ÿ mass%Mn f
O
0
mass%O ÿ mass%O
9:29
K
SiO
2
SiO
2
0
X
SiO
2
X
SiO
2
f
Si
0
mass%Si ÿ mass%Si f
2
O
0
mass%O ÿ mass%O
2
9:30
In these equations, the superscript `0' on the left side of each concentration
denotes the concentration before aluminium addition, and f stand for the
activity coefficient of the oxide in the sla g and the activity coefficient of the
element in the liquid metal, respectively.
The concentration change of an element in the metal is related to the mole
fraction change of its oxide in the slag,
X
Al
2
O
3
metal
V
metal
slag
V
slag
o
M
slag
100
1
2 M
Al
mass%Al 9:31
X
FeO
metal
V
metal
slag
V
slag
o
M
slag
100
1
M
Fe
mass%Fe 9:32
Improving process design in steelmaking 383
X
MnO
metal
V
metal
slag
V
slag
o
M
slag
100
1
M
Mn
mass%Mn 9:33
X
SiO
2
metal
V
metal
slag
V
slag
o
M
slag
100
1
M
Si
mass%Si 9:34
In the above equations,
metal
and V
metal
are the density and volume of the metal;
slag
and V
slag
are the density and volume of the slag,
o
M
slag
is the mole weight
of the slag. It is noted that the concentration change of oxygen is due to the
reactions 9.23 to 9.26. Hence,
mass%O
3
2
M
O
M
Al
mass%Al 2
M
O
M
Si
mass%Si
M
O
M
Mn
mass%Mn
M
O
M
Fe
mass%Fe 9:35
where, M
i
stands for the molar weight of the element i.
In ord er to calculate the slag composition and stee l composition at
equilibrium, equations 9.27 to 9.35 should be solved simultaneously. While
the activity coefficients of the oxides can be evaluated using the thermodynamic
model for ionic melts developed at KTH,
15,16
Wagner's model
18
could be
employed to calculate the activity coefficients of the dissolved elements in the
liquid metal. It should be pointed out that the use of the KTH model and
Wagner's model is only an example. The readers could also use other
thermodynamic models for the slag and metal. However, the principle of the
calculation would be the same.
One could also take the desulphurization into consideration by including
equations 9.21
0
and 9.22. Consequently, one more term corresponding to sulphur
should be include d in equation 9.35:
mass%O
3
2
M
O
M
Al
mass%Al 2
M
O
M
Si
mass%Si
M
O
M
Mn
mass%Mn
M
O
M
Fe
mass%Fe ÿ
M
O
M
S
mass%S 9:36
This practice is very important for the design and even the optimization of the
ladle treatment. For instance, in many steel plants, EAF slag is tapped into the
ladle along with the molten steel. In the EAF slag, the FeO content is usually
very high. One would always face the choice regarding when aluminiu m should
be added for deoxidation. A calculation as discussed in this section would reveal
that Al should definitely be added after the deslagging procedure. Big amount of
Al added to the ladle in the presence of the EAF slag would contribute mostly to
reduce the FeO in the slag and therefore help very little to reduce the oxygen
activity in the liquid metal.
384 Fundamentals of metallurgy
9.4 Kinetics ± mass transfer and heat transfer
Very often, a process is far from thermodynamic equilibrium. While a
thermodynamic analysis would reveal the driving force of the process, a
reliable estimation of the process time would require an in-depth understanding
of the reaction mechanism and good knowledge of the reaction rate.
The kinetic aspects of heterogeneous reaction have been discussed in Chapter
7. In an industrial process, the situation would be much more complicated. To
elaborate the discussion, the sintering process in a belt furnace is taken as an
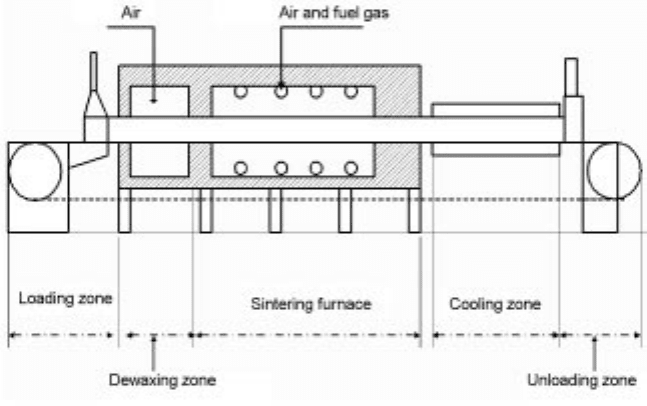
example. Belt furnaces are widely used in metallurgical industries, part icularly
for sintering process.
34,35
Figure 9.5 presents the schematic diagram of a typical
gas fired belt furnace unit. It consists of a continuous sintering furnace with a
preheating zone, a few metres of sintering zone and a cooling zone. The unit is
also equipped with a conveyance system driven by a driving unit. In the case of
sintering, the temperature profile in the furnace plays a crucial role. For instance,
too high temperature during initial part of sintering cycle could lead to premature
release of the binder and increased porosity. During the cooling part of the cycle,
the temperature needs to be well controlled to avoid undesired reactions, e.g.
reoxidation. To design the process, the following considerations must be made.
1. Mass transfer
The mass transfer can further be divided into three steps:
(a) Mass transfer in each individual particle of the sintered material.
(b) Mass transfer of the gas through the bed of the sintered material.
(c) Mass transfer in the gas phase.
9.5 Schematic diagram of a typical gas-fired belt furnace unit.
Improving process design in steelmaking 385
