Седалищев В.Н. Методы и средства измерений электрических величин

Подождите немного. Документ загружается.

Как корреляционный, так и регрессионный анализы состоят из двух

частей: расчет коэффициентов уравнения регрессии методом МНК и

статистическая оценка результатов. Если МНК можно применять при любых

статистических данных, распределенных по любому закону плотности

вероятности, то дать статистическую оценку полученным коэффициентам и

уравнению регрессии можно лишь на основе определенных теоретических

предпосылок.

Корреляционный и регрессионный анализы различаются

теоретическими предпосылками, т.е. способами статистической оценки.

Задача корреляционного анализа – исследование тесноты

корреляционной связи между случайными переменными процесса и

получение коэффициентов уравнения регрессии. Теснота корреляционной

связи исследуется путем вычисления коэффициентов парной и

множественной корреляции, взаимной и автокорреляционных функций.

Для непрерывных случайных переменных взаимная корреляционная

функция

между случайными переменными определяется формулой:

dttytx

∫

+⋅= )()(

lim)(

ττ

(14.4)

На практике обычно используют дискретные замеры через равные

промежутки времени, а интеграл заменяют суммой.

Расчет корреляционной функции является весьма трудоемкой операцией,

поэтому используют ЭВМ. Существуют хорошо отработанные программы

расчета корреляционных функций. Взаимные корреляционные функции

используются в теории планирования эксперимента для учета динамики в

объектах с непрерывными технологическими процессами.

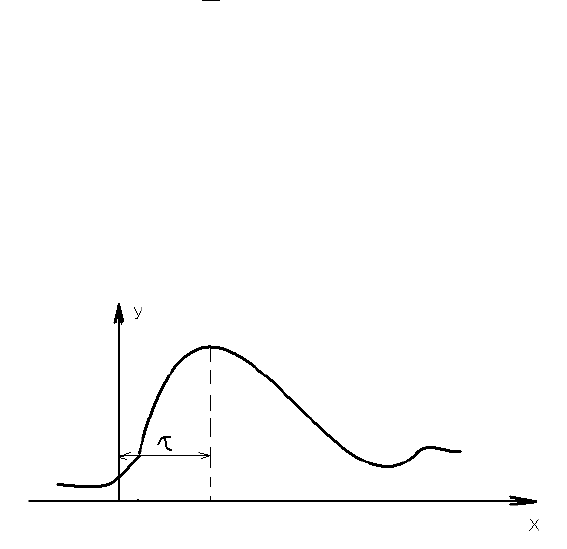
На рисунке

приведен пример типичной взаимной корреляционной функции.

Рис. 14. 1 Вид взаимной корреляционной функции.

По расположению максимума этой функции на оси времени определяется

время эквивалентного запаздывания. Физический смысл этого понятия

состоит в том, что всякий скачок функции на входе объекта наиболее полно

отражается на выходе из него только через определенный промежуток

времени.

Данный принцип применяется в устройствах измерения

скорости потока

меточными методами, например, с использованием солевых растворов.

В теории эксперимента применяют также автокорреляционные функции. По

ним оценивают величину промежутков времени между соседними

измерениями входного сигнала. Эти промежутки называются временем

корреляции.

()

xõ

SSN

xtxxtx

⋅⋅−

−

⋅

−

)])([])([

. (14.5)

Статистические критерии являются правилами, которые позволяют

делать статистические выводы о свойствах параметров генеральной

совокупности с принятым уровнем значимости. Для этой цели широко

применяют критерии Стьюдента, Пирсона, Фишера.

Теоретические предпосылки применения методики корреляционного

анализа:

• все входные и выходные случайные переменные должны подчиняться

многомерному нормальному закону распределения вероятности;

•

все случайные процессы должны быть стационарными, т.е. их средние

значения и дисперсии не должны существенно изменяться во времени;

• все выходные случайные переменные не должны быть функционально

связаны между собой;

• отдельные измерения по каждой их входных переменных должны быть

статистически независимыми;

• все входные переменные должны измеряться с пренебрежимо

малой

ошибкой, существенно меньшей шумового поля.

Перечисленные требования являются достаточно жесткими

ограничениями, однако в ряде случаев они все же удовлетворяются. Условия

многомерного нормального распределения случайных переменных сужают

область применения корреляционного анализа, поэтому они применяются

лишь для получения линейных математических моделей.

Задачи регрессионного анализа - исследование тесноты статистической

связи между входными

и выходными случайными переменными с помощью

регрессионных уравнений и коэффициентов. В простейшем случае получают

двумерное регрессионное уравнение, в котором участвует лишь одна

переменная.

Регрессионный анализ позволяет решать более широкий класс задач, чем

корреляционный анализ, и получать оценки коэффициентов нелинейности

уравнений регрессии.

Теоретические предпосылки для регрессионного анализа являются

менее жесткими:

•

случайные помехи должны иметь нормальный закон распределения;

• дисперсии выхода во всех точках факторного пространства должны

быть однородными;

• все соседние измерения по каждой входной переменной должны быть

независимыми;

• случайные помехи на выходе объекта в каждом опыте должны быть

независимы друг от друга, а также от значений входных переменных

коэффициентов уравнений регрессии.

Таким образом, при регрессионном анализе не требуется, чтобы все

входные переменные были распределены нормально.

При экспериментальном исследовании объекта качество полученных

результатов и произведенные затраты определяются организацией

эксперимента. В связи с этим, помимо исследования эффективных методов

обработки экспериментальных данных, необходимо оптимизировать сам

эксперимент по следующим параметрам: числу учитываемых входных

факторов, интервалам

варьирования и числу уровней варьирования факторов,

сочетанием их и последовательностью проведения опытов.

При проведении эксперимента необходимо включать в рассмотрение все

факторы, которые могут влиять на выходной параметр. В ходе эксперимента

последовательно можно устанавливать несколько значений уровней

факторов. Такой эксперимент называется полным факторным

экспериментом (ПФЭ). Эксперимент, в котором встречаются не все

возможные сочетания уровней факторов, называется дробным факторным

экспериментом (ДФЭ).

Если факторы варьируются на (р) уровнях, то число опытов для ПФЭ

будет

pN =

, где к – число факторов. Поэтому выбор сочетаний уровней

факторов, их числа и порядка постановки опытов является целью

планирования эксперимента.

Ортогональным называется план с попарно ортогональными вектор-

столбцами матрицы планирования. Использование критерия ортогональности

имеет целью упрощение вычислений и получение независимых оценок

коэффициентов. При этом замена любого коэффициента в модели не

изменяет

оценок остальных коэффициентов.

В ряде случаев реальные объекты имеют нелинейные зависимости.

Один из часто встречающихся видов нелинейности связан с эффектом

взаимодействия, когда значение одного фактора зависит от значения другого

фактора. Для того, чтобы найти оценку коэффициента при парном

взаимодействии, необходимо, пользуясь правилом перемножения столбцов,

получить столбец произведения двух факторов.

На рисунке представлена матрица планирования эксперимента с

варьированием двух факторов по двум уровням («+» - верхний уровень, «-» –

нижний уровень сигнала).

№ опыта

С учетом эффекта взаимодействия математическая модель запишется

следующим образом:

212,1221100

õõõõõó

, (14.6)

xxó

iii 21

2,1

. (14.7)

Столбцы (

) и

() задают планирование, и по ним непосредственно

определяются условия опытов, а столбцы (

- фиктивная переменная) и

(

) служат только для расчета.

• Матрица планирования должна обладать следующими свойствами:

симметрией т.е. сумма элементов столбца каждого фактора должна

быть равна нулю относительно центра эксперимента (центра между

уровнями);

• нормальностью, т.е. сумма квадратов элементов каждого столбца

должна быть равна числу опытов;

• ротабельностью, т.е. равенством точности предсказания

значений

отклика на равных расстояниях от центра эксперимента.

При увеличении числа входных факторов общее число опытов в ПФЭ

резко увеличивается. При построении линейных моделей имеется

возможность сокращения числа опытов за счет потери информации,

несущественной для данного вида моделей.

Пользуясь таким планированием, можно вычислить четыре

коэффициента для рассматриваемого примера. Если имеется

основание

считать, что эффект парного взаимодействия отсутствует, то последний

столбец можно представить в виде варьирования нового фактора

. Тогда

оценка коэффициентов, удовлетворяющих МНК, определяются по

выражениям:

;

óx

ii1

;

óx

ii2

;

óx

ii3

. (14.8)

Так как

в данном плане как взаимодействие

õõ

, то оценка четвертого

коэффициента является смешанной. Поставив только четыре опыта для

оценки влияния трех факторов, была использована только половина всех

возможных для данного примера вариантов. На основании данного примера

можно сделать вывод о том, что с целью уменьшения числа опытов часть

факторов целесообразно варьировать как взаимодействие.

Разрешающей способностью такой полуреплики

называют число

независимых переменных, входящих в определенный контраст. Дробные

реплики широко применяются при получении линейных моделей.

Целесообразность их возрастает по мере роста числа факторов. Если план

обладает избыточностью опытов для нахождения оценок коэффициентов

регрессионного уравнения, то он называется насыщенным.

При увеличении числа рассматриваемых факторов для уменьшения

числа экспериментов можно воспользоваться

и другими специальными

методами, например, планом в виде латинского квадрата, греко-латинского

квадрата и др. Планы второго порядка используют для нахождения

коэффициентов нелинейных моделей второго порядка.

14.5 Планирование эксперимента при поиске оптимальных условий

Задача оптимизации одна из наиболее распространенных задач,

встречающихся в практике измерительного эксперимента. Определение

наилучших в некотором смысле условий, значений параметров и уровней

факторов является во многих случаях основной целью эксперимента. Такого

рода оптимизационные проблемы возникают, в частности, в следующих

случаях:

• при управлении

технологическими процессами и установками, где

необходимо достижение требуемой производительности при

наилучшем качестве и минимальных затратах;

• при проектировании устройств для подбора параметров,

обеспечивающих наилучшие эксплуатационные характеристики;

• при создании новых образцов сплавов и синтезе химических веществ,

обладающих определенными свойствами;

• при решении задач вычислительного характера, например, численное

построение плана эксперимента, оптимального

в соответствии с

выбранным критерием.

Методы экспериментальной оптимизации. С математической точки

зрения задача оптимизации может быть сформулирована как нахождение

значений управляемых факторов объекта исследования, при которых его

отклик или критерий оптимизации достигает экстремального значения.

Экстремальная точка при этом должна находиться с учетом ограничений на

диапазон изменения управляемых факторов. Все методы

оптимизации

можно разделить на два основных класса:

• теоретические методы, применяемые в случаях, когда задача

полностью определена с математической точки зрения и допускает

применение известных аналитических методов оптимизации,

например, дифференциального или вариационного исчисления, а

также линейного, целочисленного и динамического

программирования;

• экспериментальные методы, используемые в условиях, когда

функция отклика не известна

и имеется возможность измерить ее

значение при различных комбинациях величин факторов.

Экспериментальные методы характерны как для исследования

различного рода физических объектов, так и для задач теоретического плана,

если аналитические методы по тем или иным причинам не эффективны и

приходится использовать численные методы решения. Главное отличие

подобных задач от оптимизационных процедур

чисто вычислительного плана

– это присутствие неконтролируемых факторов, т.е. наличие шума

случайного характера, а также ряд случаев детерминированного дрейфа. В

этой связи особенно важным является решение вопросов эффективности

различных методов оптимизации при наличии помех, сходимости

алгоритмов и точности их функционирования в данных условиях.

Экспериментальные методы можно разделить на две группы:

поисковые методы и методы, основанные на предварительном получении

эмпирической модели объекта, описывающей его поведение в области

оптимума.

В поисковых методах осуществляется последовательное локальное

изучение поверхности отклика. Экспериментальное значение при этом

достигается с помощью последовательных процедур, включающих в себя

этапы:

• определение по результатам специально

спланированного

эксперимента направления движения из некоторой точки, в

окрестностях которой проводится эксперимент;

• организацию движения в найденном направлении;

• повторение указанных этапов до достижения точки оптимума.

В методах оптимизации, основанных на предварительном

экспериментальном получении математической модели объекта, фактически

предусматривают в отличие от поисковых, изучение не локальных, а общих

свойств поверхности

отклика в определенной области факторного

пространства, где предположительно находится оптимум. В качестве

подобной модели могут использоваться регрессионные модели в виде

полного квадратичного полинома. При этом само определение точки

экстремума осуществляется с помощью известных теоретических методов,

например, дифференциального исчисления или линейного

программирования. Для методов оптимизации наибольший интерес

представляет проблема планирования эксперимента,

обеспечивающего

наивысшую точность в определении координат оптимума, а также

рассмотрение специфики, возникающей при использовании стандартных

аналитических методов нахождения экстремального значения применительно

к статистическим моделям, построенным экспериментально.

Использование ЭВМ при расчетах сложных процессов является

принципиально необходимым для проведения экспериментов. Это дает

возможность проводить имитационный эксперимент для объектов с

адекватными математическими моделями.

Понятие имитационного или вычислительного эксперимента впервые

было сформулировано в 1945 году в связи с моделированием траектории

движения нейтронов. В дальнейшем вычислительный эксперимент стал

широко применяться в различных областях науки и техники.

Выделяют два класса принципов имитационного моделирования:

• эксперименты, использующие описание исследуемого объекта с

помощью уравнений;

• эксперименты, использующие непосредственно описание

объекта.

Первый класс, в конечном счете, сводится ко второму. Так, например,

решать уравнение теплопроводности можно, моделируя броуновское

движение молекул, т.е. вычисляя последовательно местоположение молекул.

Проведение имитационного моделирования эксперимента с помощью

ЭВМ состоит из следующих этапов:

• описание явления или процесса, подлежащего моделированию;

• определение количественных характеристик, доступных

наблюдению или измерению;

• проведение необходимых упрощений и выбор типа математической

модели; перевод модели на язык ЭВМ, т.е. выбор языка

программирования и создание программы;

• анализ

результатов расчета и сравнение с результатами натурного

эксперимента или косвенными данными, имеющимися в

распоряжении.

Модели, изучение которых проводится с помощью имитационного

эксперимента, отличаются от других возможностью наиболее полного учета

всех факторов по сравнению с моделями, допускающими только

аналитическое исследование.

Модели принято подразделять на детерминированные и

вероятностные. Простейшим примером детерминированной модели

может

служить модель системы, описываемой дифференциальным уравнением или

системой таких уравнений. Детерминированные модели такого типа

исследуются аналитически, если они достаточно просты, и с использованием

ЭВМ. Имитационный эксперимент с помощью ЭВМ состоит в численном

решении соответствующих уравнений.

Примером вероятностных моделей являются в первую очередь системы

массового обслуживания. Такие системы часто невозможно

исследовать

другими способами, кроме имитационного моделирования. Они

характеризуются: случайным потоком заявок; случайным временем

обслуживания.

Современные ЭВМ снабжены датчиками случайных чисел, которые

могут присваивать указанной переменной значение, равное реализации

равномерно распределенной случайной величины. С их помощью получают

разнообразные законы распределения случайных величин. Имитационный

эксперимент имеет большие возможности, чем натурный, так как

при этом

имеется возможность изменения параметров закона распределения

случайных величин.

Литература

1. Электрические измерения неэлектрических величин / Под ред.

П.В. Новицкого. – Л.: Ленинградское отд. Энергия, 1975.

2. Асатурян В.И. Теория планирования эксперимента. – М.: Радио и

связь, 1983.

3. Измерение электрических и неэлектрических величин /

[Н.Н.

Евтихиев, Я.А. Купершмидт, В.Ф. Папуловский и др.] – М.:

Энергоатомиздат, 1990.

4. Ильин В.А. Телеуправление и телеизмерение /В.А. В.А. Ильин. –

3-е изд., перераб. и доп. М.: Энергоатомиздат, 1982.

5. Информационно-измерительная техника и технологии / [В.И.

Калашников, С.В. Нефедов, А.Б. Путилин и др.]; под ред. Г.Г.

Раннева. – М.: высш. шк., 2002.

6. Спектор С.А. Электрические измерения

физических величин6

Методы измерений / С.А. Спектор. – Л.: Энергоатомиздат.

Ленингр. отд-ние, 1

87.

7. Цапенко М.П. Измерительные информационные системы:

структуры и алгоритмы, системотехническое проектирование /

М.П. Цапенко. – 2-е изд. перераб. – М.: «Энергоатомиздат», 1985.

8. Электрические измерения: учеб. Пособие / [В.Н. Малиновский,

Р.М. Демидова-Панферова, Ю.Н. Евлаков и др.]; под ред. В.Н.

Малиновского. М.: Энергоатомиздат, 1985.

Островский Л.А. Основы общей теории электроизмерительных

устройств. «Энергия», Л., 1971.

10.

Основы метрологии и электрические измерения: Учебник для вузов / Б.Я.

Авдеев, Е.М. Антонюк, Е.М. Душин и др.; Под ред. Е.М. Душина. – 6-е изд.,

перер. И доп. – Л.: Энергоатомиздат. Ленингр. отд-ние, 1987.

ОГЛАВЛЕНИЕ

Введение…………………………………………………………...3

Глава 1. Общая характеристика методов и средств измерений

1.1 Классификация измерений

1.2 Виды измерений

1.3 Методы измерений

1.4 Классификация средств измерений

1.5 Основные характеристики средств измерений

Глава 2. Устройство и принцип работы аналоговых

электромеханических измерительных приборов

2.1 Аналоговые измерительные приборы электромеханической системы

2.2 Измерительные приборы магнитоэлектрической системы

2.3. Приборы электромагнитной системы

2.4 Приборы электродинамической системы

2.5 Приборы электростатической системы

2.6 Индукционные измерительные приборы

2.7 Условные обозначения, наносимые на шкалу прибора

электромеханической системы

Глава 3. Электромеханические приборы с преобразователями

3.1 Шунты, добавочные резисторы

3.2 Измерительные механизмы с выпрямителями и термопреобразователями

3.3 Измерительные трансформаторы тока и напряжения

3.4 Измерительные усилители

Глава 4. Аналоговые электронные измерительные приборы

4.1 Классификация электронных измерительных приборов

4.2 Электронные вольтметры

Глава 5. Генераторы электрических сигналов

Глава 6. Приборы для исследования параметров электрических

сигналов

6.1 Основные характеристики электронных осциллографов

6.2 Принцип работы электронного осциллографа

Глава 7. Измерительные мосты и компенсаторы

7.1 Мостовые схемы

7.2 Устройство и принцип работы измерительных мостов и компенсаторов

Глава 8. Цифровые измерительные приборы

8.1 Устройство и принцип работы цифроввых измерительных приборов

8.2 Аналого-цифровые преобразователи

8.3 Цифровые осциллографы

Глава 9. Методы и средства измерения параметров

электрической цепи

9.1 Измерение постоянного тока и напряжения

9.1.1 Измерение тока и напряжения с использованием метода

непосредственной оценки

9.1.2 Измерение тока и напряжения с использованием метода сравнения с

мерой

9.1.3 Измерение переменного тока и напряжения

9.2 Измерение электрической мощности и энергии

9.3 Электронные ваттметры

9.4 Методы и средства измерения частоты следования сигналов

9.4.1 Использование метода перезаряда конденсатора

для измерения частоты

следования сигналов

9.4.2 Резонансный метод измерения частоты

9.4.3 Использование методов сравнения для измерения частоты

9.4.4 Электронно-счетный частотомер

9.4.5 Цифровое устройство для измерения периода следования сигналов

9.5 Измерение фазового сдвига

9.6 Измерение фазового дрожания цифрового сигнала

Глава 10. Измерение параметров элементов электрической

цепи

10.1 Электромеханические омметры

10.2 Электронные омметры

10.3 Реализация метода дискретного счета в омметрах

10.4 Реализация метода уравновешивающего преобразования в измерителях

параметров электрической цепи

10.5 Резонансный метод измерения параметров элементов цепи

10.6 Измерение емкости

10.7 Измерение индуктивности

Глава 11. Измерение магнитных величин

11.1 Измерение магнитного потока

11.2 Измерение магнитной индукции и напряженности магнитного поля

Глава 12. Методы спектрального анализа сигналов

12.1 Фильтровые анализаторы спектра

12.2 Измерение параметров спектра модулированных сигналов

12.3 Измерение нелинейных искажений

12.4 Измерение уровней передачи сигнала и степени его затухания

Глава 13. Автоматизация измерений

13.1 Общая характеристика и проблемы автоматизации измерений

13.2 Измерительные информационные системы (ИИС)

13.2.1 Виды и структуры измерительных информационных систем

13.2.2 Основные компоненты ИИС

13.2.3 Математические модели и алгоритмы измерения ИИС

13.2.4 Характеристика ИИС

13.2.5 Виды ИИС

13.3 Телеизмерительные системы

13.4 Поисковая система телеизмерений

13.5 Система автоматического контроля

13.6 Системы технической диагностики

13.7 Системы распознания образов

13.8 Статистические

измерительные системы

13.9 Компьютерные измерительные системы (КИС)

13.10 Интеллектуальные информационно-измерительные системы (ИИИС)

13.11 Принципы построения интеллектуальных и виртуальных

измерительных устройств

13.12 Основные принципы передачи измерительной информации

13.13 Интерфейсы ИИС

13.14 Принципы построения беспроводных систем сбора первичной

измерительной информации

13.15 Метрологическое обеспечение ИИС

Глава 14. Подготовка и проведение измерений

14.1 Планирование эксперимента

14.2 Организация проведения измерений

14.3Вопросы оптимизации проведения измерительного эксперимента

14.4 Регрессионный анализ и планирование эксперимента

14.5 Планирование эксперимента при поиске оптимальных условий

Литература