Schulz M. Control Theory in Physics and Other Fields of Science: Concepts, Tools, and Applications

Подождите немного. Документ загружается.

126 5 Chaos Control

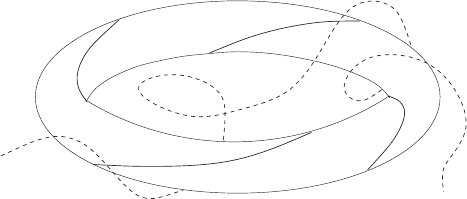
Fig. 5.1. Schematic representation of a closed orbit covering a torus and a chaotic

trajectory as typical elements of the phase space

The ﬁrst guess is that because of this argument most trajectories are wildly

erratic and run quite far from initially neighbored trajectories. Surprisingly,

it can be shown that, in contrast to this presumption, a ﬁnite volume of the

admissible domain has the familiar structure of imbedded tori covered with

dense trajectories. This is the Kolmogorov–Arnold–Moser theorem [1, 52, 53].

Although the main statement of this theorem is the result of a perturbation

theory with an integrable Hamiltonian as reference model, it should be also

applicable to strongly nonlinear coupled systems.

In particular, the Kolmogorov–Arnold–Moser theorem is important for

the characterization of mechanical systems with a small number of degrees of

freedom. Several early [54, 55] as well as recent numerical investigations show

that the relative part of the region containing apparently random trajectories

increases rapidly with the complexity of the system, and we arrive the mixing

behavior discussed in Sect. 1.2.

This is also an important remark for the closed trajectories discussed

above. Under the consideration that the system allows isolated tori with closed

trajectories, these orbits are strongly unstable. A small change of the initial

conditions or the system parameters transfers the system from its unstable

period motion either to another torus with a conditionally periodic motion or

to an apparently chaotic trajectory (Fig. 5.1).

5.1.3 Nonconservative Systems

Conservative mechanical systems are either in a permanent motion or they

are ﬁxed for all times. In contrast to this behavior, the evolution equations of

nonconservative systems can have stable and/or unstable ﬁxed points and/or

attractors in the phase space. That means such systems can gradually reduce

or increase their dynamical mobility. However, this behavior is only possible

because such systems exchange permanently energy and matter with exter-

nal sources and sinks or their initial state is far from the thermodynamical

equilibrium. In many cases (see below), the equations of motion reﬂect this

exchange only by several constant parameters, so that one have the ﬁrst im-

pression that these equations are on the same level as mechanical equations.

5.1 Characterization of Trajectories in the Phase Space 127

In fact, nonconservative evolution equations usually describe only the time-

dependence of a few relevant variables which seems to be representative for

the characterization of the whole system whereas all other degrees of freedom

are hidden in several parameters and some ﬂuctuation terms which are not

considered at the deterministic level; see Sect. 1.3.2. As an example, let us

consider a chemical reaction model, the Lotka model [56], which is described

by the reaction scheme

A + X−→2X

X + Y−→2Y

Y−→B.

(5.9)

The variables of the system are the concentrations of the components X and

Y while the complicated intrinsic microscopic dynamics of the molecules is

described by three kinetic coeﬃcients k

, k

,andk

deﬁning the velocity of

the ﬁrst, second, and third reaction. The kinetic equations of this reaction are

simply given by

˙x = k

x − k

˙y = k

xy − k

(5.10)

with x being the concentration of the component X, y is the concentration of

Y,andc

is the concentration of A. We keep the concentration of A constant.

This is always possible by controlled supply from external sources. In this

sense, the component A can be interpreted as the source of the process, while

the component B represents a chemical sink.

The concentrations x and y form the phase space of the Lotka model. The

evolution equations have a partially unstable ﬁxed point for x = y =0,which

means that all initial conditions x

=0,y

= 0 converge to the ﬁxed point

for suﬃciently long times while the initial conditions x

=0andy

= 0 lead

to divergent behavior x →∞for t →∞. All other, nonzero initial conditions

yield closed cycles. These orbits can be calculated in the case of the Lotka

model analytically. We obtain from (5.10)

x − k

) y

− k

y) x

, (5.11)

which can be integrated, and we arrive at

x + y − x

− y

−

. (5.12)

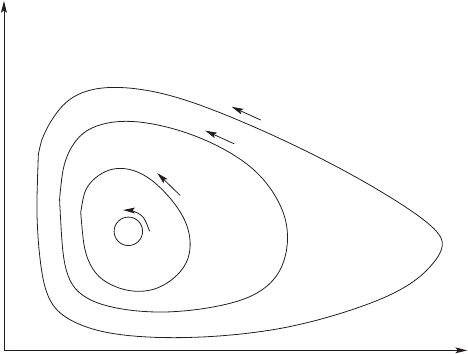
Figure 5.2 shows a representation of these closed orbits in the phase space.

The Lotka model is a candidate of a large class of similar evolution processes.

In general, all these equations may be formally written in the form

X = F (X).

Possible ﬁxed points X

follow from the requirement F (X

)=0.Aswehave

discussed in Sect.3.1.3, the stability of ﬁxed points is mainly determined by

the eigenvalues of the matrix ∂F(X

)/∂X

. The type of diﬀerent ﬁxed points

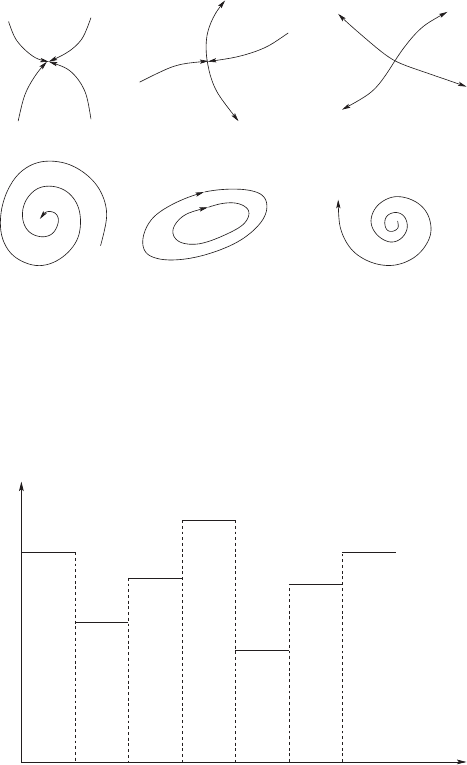
increases rapidly with increasing dimension of the phase space. So we have for

N = 1 only two standard types of ﬁxed points (stable and unstable), while

128 5 Chaos Control

Fig. 5.2. The motion of the Lotka model through its two-dimensional phase space

the classiﬁcation scheme for N = 2 shows six standard cases; see Fig. 5.3.

Furthermore, the evolution of a two-component system may converge into

a stable limit cycle (attractor). Finally, we remark that chaotic trajectories

can be observed also for nonconservative systems. A standard example is the

Belousov–Zhabotinskii reaction [57]. Although the behavior of nonconserva-

tive evolution equations oﬀers an apparently bewildering variety of diﬀerent

possible scenarios, both conservative and nonconservative systems may be

controlled with similar techniques. In several cases, especially close to stable

ﬁxed points or attractors, the control of nonconservative evolution equations

becomes simpler as the control of conservative equations of motion.

5.2 Time-Discrete Chaos Control

5.2.1 Time Continuous Control Versus Time Discrete Control

Let us now assume that the motion of a mechanical system is strictly conﬁned

to a ﬁnite domain, G,oftheN-dimensional phase space P and that the control

of a system takes place at well-deﬁned times t

with t

< ···<t

< ···.

In other words, the vector control function u can be replaced by a set of

parameters

u → u

(µ)



(µ)

,...,u

(µ)



, (5.13)

which are constant for each period [t

µ+1

] with (µ =0, 1,...) and which

change their values only at the control times t

, see Fig. 5.4. Let us further

assume that the state vector X has reached the value X

(µ)

at time t

in course

of the controlled motion of the system through the phase space P. Then we can,

5.2 Time-Discrete Chaos Control 129

abc

Fig. 5.3. Six standard ﬁxed points in a two-dimensional phase space. Both the

eigenvalues λ

and λ

of the matrix ∂F(X

)/∂X

can be (a)Reλ

< 0, Reλ

< 0,

Imλ

=0andImλ

= 0 (stable regime), (b)Reλ

> 0, Reλ

< 0, Imλ

= 0 and

Imλ

= 0 (instable regime), (c)Reλ

> 0, Reλ

> 0, Imλ

=0andImλ

(instable regime), (d)Reλ

> 0 and/or Reλ

> 0, Imλ

= 0 and/or Imλ

=0

(instable regime), (e)Reλ

=0,Reλ

=0,Imλ

=0orImλ

= 0 (metastable

regime), and (f)Reλ

< 0, Reλ

< 0, Imλ

= 0 and/or Imλ

= 0 (nstable regime)

(0)

(1)

(2)

(3)

(4)

(5)

(6)

Fig. 5.4. Time discrete control on a continuous time scale

at least formally, solve the evolution equation (2.53) for the period [t

µ+1

]

considering the initial conditions X(t

)=X

(µ)

, and we obtain

X(t)=Φ(t, t

(µ)

)fort

<t<t

µ+1

. (5.14)

Obviously, the current state is a function of the initial state X

(µ)

, the control

(µ)

chosen at the time t

and the current time t. In particular, we obtain for

t = t

µ+1

(µ+1)

= Φ(t

µ+1

(µ)

) , (5.15)

130 5 Chaos Control

which is a functional relation between the states of the system for two control

times. If the underlying evolution equations are an autonomous system of

diﬀerential equations, then (5.15) reduces to

(µ+1)

= Φ(t

µ+1

− t

(µ)

) (5.16)

and further, if we focus on equidistant control times t

µ+1

= t

+ ∆t

(µ+1)

= Φ(X

(µ)

) , (5.17)

where the time diﬀerence is now a simple system parameter which is no longer

explicitly considered. This is a discrete equation of motion. Because of the

facts that (5.17) is the solution of the original evolution equation (2.53) for

the time period [t

µ+1

] and that the dynamics of the system is conﬁned to

the region G, we automatically get the mapping Φ : G → G. The discrete

series

(1)

(2)

,...,X

(µ)

,...

can be interpreted as a trace of the com-

plete trajectory of the system, which means in the case of a constant control

we should expect a discrete realization of a periodic motion, a conditionally

periodic motion or a chaotic trajectory similar to the scenarios discussed in

Sect. 5.1.2.

Another very instructive method leading to time-discrete controls are re-

lated to Poincar´e plots. To this aim we imagine that we set up a N

screen

dimensional (N

screen

<N) screen to the phase space deﬁned by the

(N − N

screen

)-component screen equation s (X) = 0. Every time the system

crosses this screen, we make a record of the position and we may change the

control function. The set of positions at the screen is called a Poincar´e plot;

see Fig. 5.5. The solution of the complete equation of motion allows us again

Fig. 5.5. Two-dimensional Poincar´e plot generated from a closed orbit in a three-

dimensional phase space

5.2 Time-Discrete Chaos Control 131

to ﬁnd a mapping of type (5.17). The only diﬀerence to the ﬁrst type of dis-

crete equations is that the control no longer takes place for equidistant times

but for all times t

satisfying the screen condition s(X(t

)) = 0 for a given

trajectory.

Discrete evolution equations are not only derivable from mechanical equa-

tions

, they are also characteristic for modelling several processes in physics,

chemistry, biology or economics where the internal dynamics of the system is

more or less unknown, but the input



(µ)



and the output X

(µ+1)

are

connected by deterministic rules. In this sense, mapping (5.17) is not neces-

sarily the result of a well-deﬁned time-continuous evolution equation, as we

have argued above, it is also possible that such laws are deﬁned empirically

on the basis of a suﬃciently large experience. A typical example concerns the

exploitation of a Fishery. This example is a very prominent idealized model

for understanding the management of renewable resources [58, 59]. The re-

source stock, i.e., the biomass of the ﬁshes, at the end of a period [t

µ−1

]is

denoted by x

(µ)

. With external intervention by ﬁshing, the biological repro-

duction yields the biomass x

(µ+1)

at time t

µ+1

given by x

(µ+1)

= f(x

(µ)

It is usual to assume that f(x) ∼ x for small x (corresponding to a dom-

inant reproduction of the species in a suitable environment) and f(x) → 1

for x →∞(corresponding to saturation eﬀects due to the limited sources

of foods and due to the presence of predatory ﬁshes). However, if y

(µ+1)

the harvested in the period [t

µ+1

] then the stock at the end of this pe-

riod is given by x

(µ+1)

= f(x

(µ)

) − y

(µ+1)

. Fish harvesting is not costless.

In particular, the harvest depends on the biomass resource available for ex-

ploitation, x

(µ+1)

, and the necessary labor eﬀort, z

(µ+1)

, for these period,

(µ+1)

= g(x

(µ+1)

(µ+1)

) with g an increasing, usually concave function in

both arguments. Finally, we express the eﬀort, z

(µ+1)

, as a function of the har-

vest and the available biomass of ﬁshes by z

(µ+1)

= h



(µ+1)

(µ+1)



with h

increasing in its ﬁrst argument and decreasing in its second. Hence, the tree

recursion relations

(µ+1)

= f(x

(µ)

) − y

(µ+1)

= g(f(x

(µ)

),z

(µ+1)

)

(µ+1)

= h



(µ+1)

,f(x

(µ)

)



(5.18)

can be solved in order to obtain the closed recursive relation for the evolution

of current resource stock x

(µ)

→ x

(µ+1)

This example is only one candidate of a large class of empirically con-

structed discrete evolution equations. Other examples are logistic map dis-

cussed below, economic growth models [21, 22], forest management models

[19, 20], or the price policy of monopolist [18, 23], but also the mathematical

process of generating random numbers by pseudorandom number generators

[10].

In contrast that is a rather rare situation and it is only reasonable if the discrete

time points play a special role, e.g., in the present case of a discrete control.

132 5 Chaos Control

A very broad class of physical applications of discrete evolution equations

is cellular automata models. Here, relatively simple interaction rules allow

the description of complex phenomena [24, 46, 47, 48, 49, 50, 51] such as

self-organized criticality [29, 37], evolution of chemically induced spiral waves

[38], oscillations and chaotic behavior of states [38, 39, 51], forest ﬁres [40],

earthquakes [41, 42, 43], discrete mechanics [44], statistical mechanics [45],

the dynamics of granular matter [29, 32], soliton excitations [33], and ﬂuid

dynamics [34, 35]. Other applications belong to various domains in biology

[36], including neuroscience [30, 31], and the dynamics of traﬃc systems [25,

26, 27, 28].

5.2.2 Chaotic Behavior of Time Discrete Systems

First of all, we will discuss the dynamic behavior of discrete equations of

motion for the trivial control u

(µ)

= λ =const. In this case, we obtain

(µ+1)

= Φ(X

(µ)

,λ) , (5.19)

and the time evolution of the series

(0)

(1)

(2)

,....

. follows from the

recursive application of the function Φ on a given initial state X

(0)

. Let us

study the standard example of a logistic map in order to get an impression

about the time behavior of discrete evolution equations. The logistic map has

a one-component state and is deﬁned by the recursion law

(µ+1)

= λx

(µ)



1 − x

(µ)



= φ

log

(µ)

) (5.20)

with the one-component control parameter λ. This model has already been

introduced by Verhulst 1845 to simulate the growth of a population in a closed

area [11]. Other applications related to economic problems are used to explain

the growth of a deposit under progressive rates of interest [12].

As found by several authors [13, 15, 16, 17] the iterates x

(µ)

(µ =0, 1,...)

display, as a function of the parameter λ, rather complicated behavior that

becomes chaotic at large λ, see Fig. 5.6. The chaotic behavior is not tied to

the special form of the logistic map (5.20). Thus, the following results are

also characteristic of other functions Φ in (5.19). In particular, the transition

from regular (but not necessary simple) behavior to the chaotic regime during

the change of an appropriate control parameter is universal behavior for all

one-component discrete equations, x

(µ+1)

= f(x

(µ)

), in which the function φ

has only a single maximum in the properly rescaled unit interval 0 ≤ x

(µ)

≤ 1.

It should be remarked that other discrete equations with chaotic proper-

ties, for instance, several types of sometimes so-called second-order

discrete

We remark that second-order equations with one component can be rewritten

into the standard form (5.19) with two components



(µ+1)







(µ)



(µ)



From this point of view, it is not necessary to consider the order of the diﬀerence

equation as a relevant property.

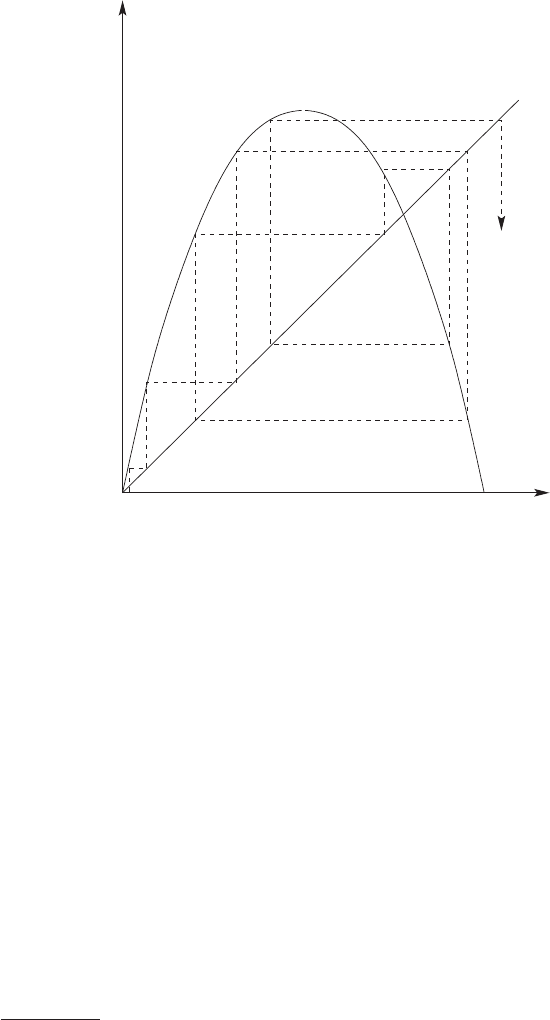
5.2 Time-Discrete Chaos Control 133

log

(x)

Fig. 5.6. Geometrical construction of the sequence x

(1)

,...,x

(µ)

,...: The special

schematic representation corresponds to a chaotic dynamics, starting from the initial

value x

close to the unstable ﬁxed point x

=0.Notethatφ = x is the reﬂection

line deﬁning the successive mapping x

→ x

µ+1

equations x

(µ+1)

= f(x

(µ)

(µ−1)

) may belong to other universality classes

However, most of the properties which are valid for the logistic map (5.20)

hold at least qualitatively also for other diﬀerence equations.

Let us brieﬂy discuss the main properties of the logistic map. The logistic

map x

(µ)

→ x

(µ+1)

has two ﬁxed points, x

=0andx

=1− λ

−1

satisfying

= φ

log

). The stability analysis of discrete evolution equations considers,

just as in the case of diﬀerential equations, see Sect. 3.1.3, weak perturbations

of the ﬁxed points, x

(µ)

= x

+ ε

. Thus we obtain ε

µ+1

= Λε

+ o(ε

) where

the so-called multiplier Λ is given by Λ = φ



log

). Obviously, for |Λ| < 1the

ﬁxed point is linearly stable. Conversely, if |Λ| > 1 the ﬁxed point is unstable.

The stability of the marginal case |Λ| = 1 cannot be decided in the framework

of the linear stability analysis, and it requires a more detailed analysis.

For small control parameters, λ<1, the quantity x

(µ)

develop toward the

stable ﬁxed point x

= 0 because φ



log

(0) = λ<1. For 1 <λ<3, we get the

That means the number of components considered in (5.19) deﬁnes essentially

the behavior of the time series

(0)

(1)

,...

134 5 Chaos Control

multiplier φ



log

(1 − λ

−1

)=2− λ so that here the ﬁxed point x

=1− λ

−1

becomes stable.

Both ﬁxed points are unstable for λ>3. We call λ

= 3 the ﬁrst critical

value of the control parameter. Now we observe a stable oscillation of period

two with the two alternating values

and x

which are related together via

the equations

= φ

log

)andx

= φ

log

). Of course, both values x

and

are stable ﬁxed points of the second-iterate map φ

(2)

log

(x)=φ

log

(φ

log

(x)).

In fact, we obtain

1/2

2λ



λ +1±



(λ − 3)(λ +1)



(5.21)

and the corresponding multiplier of the 2-cycle, Λ =4+2λ − λ

, satisﬁes

|Λ| < 1for3<λ<1+

√

Thus, the unique asymptotic solution x

(µ)

∝ x

=1− λ

−1

for µ →∞

splits into alternating solutions

and x

while crossing the border λ =3.At

λ = 3 the values of

and x

coincide and equal x

=1− λ

−1

=2/3which

shows that the 2-cycle bifurcates continuously from x

. This bifurcation is

sometimes denoted as pitchfork bifurcation.

Above the second critical value of the control parameter, λ

=1+

√

6, the

2-cycle splits into a 4-cycle. Further period-doublings to cycles of period 8,

16, ..., 2

,...occur as λ increases, Fig. 5.7. The critical values λ

where the

number of ﬁxed points changes from 2

m−1

to 2

scale like λ

= λ

∞

−Cδ

−m

Here, C and λ

∞

are speciﬁc parameters (λ

∞

=3.56994 ... for the logistic

map), while the Feigenbaum constant δ =4.6692 ... is a universal quantity

[9, 14, 15]. All the cycles can be interpreted as attractors of a ﬁnite set of

points.

For r>r

∞

the asymptotic behavior of the series x

(0)

,...,x

(µ)

,...becomes

unpredictable. More precisely, we must say that for certain values of λ>λ

∞

the sequence never settles down to a ﬁxed point or a periodic cycle. Instead

the asymptotic behavior is aperiodic and therefore chaotic. The corresponding

attractor changes from a ﬁnite to an inﬁnite set of points.

However, the region for λ>λ

∞

shows a surprising mixture of several

periodic p-cycles (p =3, 5, 6,...) and the true chaos. The periodic cycles occur

in small λ-windows among other windows with chaotic behavior and also show

successive bifurcations p,2p,...2

p,....Thecorrespondingλ-values scale like

the above-mentioned Feigenbaum law, only the nonuniversal constants C and

∞

are diﬀerent.

Furthermore, periodic triplings 3

p, and quadruplings 4

p occur at λ



∞

− C



−n

with diﬀerent nonuniversal constants λ



∞

and C



and diﬀerent

Feigenbaum constants which are again universal for the type of the bifurcation,

e.g.,

δ =55.247 ..., for the tripling.

Besides the stable ﬁxed points, the stable periodic cycles, and the chaotic

sets we also ﬁnd a set of unstable ﬁxed points and periodic orbits which

are partially the continuation of the stable regimes to control parameters

above the corresponding critical value. For example, the above-introduced

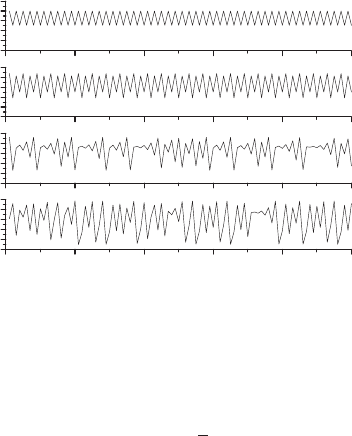
5.2 Time-Discrete Chaos Control 135

0 20 40 60 80 100

0.0

0.2

0.4

0.6

0.8

1.0

0.0

0.2

0.4

0.6

0.8

1.0

0.0

0.2

0.4

0.6

0.8

1.0

0.0

0.2

0.4

0.6

0.8

1.0

Fig. 5.7. Varios dynamic regimes of the discrete logistic map recursion law: periodic

oscillations with period 2, λ =3.2(top), periodic oscillations with period 4, λ =3.5,

chaotic behavior with λ =3.7 and chaotic behavior with λ =3.9(bottom)

ﬁxed points x

=0andx

=1− λ

−1

and the 2-cycle (5.21) also exists as

unstable orbits for λ>3andλ>1+

√

6, respectively, and they are also

embedded in the chaotic set.

Finally, we remark that the attraction of an arbitrary initial condition

(0)

∈ [0, 1] to a stable orbit or ﬁxed point indicates, from a physical point

of view, a hidden dissipative process. In other words, the logistic map has no

background in the conservative classical mechanics.

On the other hand, the discrete trajectories obtained from the recursion

law (5.17) for mechanical equations of motion can be directly obtained from

the continuously trajectories discussed in Sect. 5.1.2 by marking the positions

at the discrete times t

. Although there are no ﬁxed points and attractive or-

bits, we again ﬁnd chaotic sets embedded within it a large number of unstable

periodic orbits.

5.2.3 Control of Time Discrete Equations

As we have remarked in the previous chapter, a chaotic set on which the

trajectory of the chaotic process lives embeds within it a large number of

unstable periodic orbits. Let us assume that the control aim consists in the

realization of one of these ﬁnite orbits of periodicity m which may be deﬁned

by the ﬁnite set C

(1)

(2)

,...,Y

(m)

and the periodic boundary

condition Y

(n+m)

= Y

(n)

. Obviously, this control aim can be interpreted

as a discrete version of a special tracking problem. The mapping between

consecutive values of Y are simply given by the law

(µ+1)

= Φ(Y

(µ)

,λ) (5.22)

for a well-deﬁned ﬁxed control λ, i.e., we consider that the set C

contains

m unstable solutions of