Schlick T. Molecular Modeling and Simulation: An Interdisciplinary Guide

Подождите немного. Документ загружается.

472 14. Molecular Dynamics: Further Topics

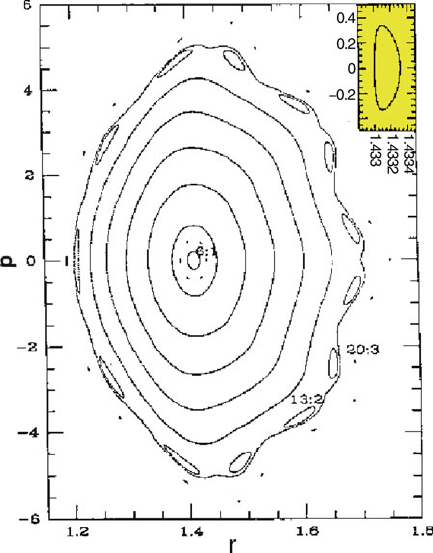
Figure 14.2. Morse oscillator phase diagrams obtained from the leapfrog Verlet integrator

with Δt =2fs at increasing initial energies. Resonances of order 6 and higher can be

noted. One of the inner-most islands (near the 6:1 label) is enlarged in the inset to show

that each corresponds to a closed orbit. See [821] for details.

Section 14.6 presents a resonance analysis for the implicit-midpoint (IM)

scheme, and Box 14.5 derives IM’s resonance condition (based on its phase-space

rotation ω

eﬀ

). Figure 14.16 illustrates resonance for a nonlinear system for both

Verlet and IM.

14.3 Multiple-Timestep (MTS) Methods

14.3.1 Basic Idea

MTS schemes were introduced in the 1970s [1232,1243] in an effort to reduce the

computational cost of molecular simulations. Savings can be realized if the forces

due to distant interactions are held constant over longer intervals than the short-

range forces. Standard integration procedures can then be modiﬁed by evaluating

the long-range forces less often than the short-range terms. Between updates, the

slow forces can be incorporated into the discretization as a piecewise constant

14.3. Multiple-Timestep (MTS) Methods 473

Table 14.2. Stability limit and resonant timestep formulas for the Verlet scheme, with

numerical values for a vibrational mode with period T

=10fs.

n, res. order

Δt

n:1

(ω)Δt

n:1

) Δt

n:1

for MD

2 2/ω 0.318 T

3.2 fs

[= T

/π]

√

3/ω 0.276 T

2.8 fs

√

2/ω 0.225 T

2.3 fs

5 1.176/ω 0.188 T

1.9 fs

[=2sin(π/5)/ω]

6 1/ω 0.159 T

1.6 fs

[= T

/2π]

For n =2, we have the linear stability condition.

To compare resonance in Verlet to implicit-midpoint integration (see end of chapter), consider

the analogous resonant timesteps Δt

n:1

for n =3, 4, 5, 6 of 5.5, 3.2, 2.3, and 1.8 fs, respectively,

for the implicit-midpoint scheme.

function (via extrapolation) or as a sum of delta functions (via impulses). See

Figure 14.4 for a schematic illustration of these two approaches.

To illustrate, in the discussion below we consider below a force splitting scheme

that involves three components for updating the fast, medium, and slow forces:

fast

, F

med

,andF

slow

with corresponding timesteps

Δτ ≤ Δt

≤ Δt.

The timesteps are related via the ratios

=Δt

/Δτ,

=Δt/Δt

, (14.26)

r = k

=Δt/Δτ,

where k

and k

are integers. Note that when k

= k

=1we have a single-

timestep (STS) method.

14.3.2 Extrapolation

A simple, Verlet-based, extrapolative force-splitting approach is best formulated

on the basis of position Verlet (eq. (13.15)) since the fast and medium forces

are evaluated at the middle of the corresponding interval rather than at the be-

ginning (and end). In programming style, where new iterates overwrite the old

(i.e., X ← X + ···), this extrapolative force-splitting scheme can be written

as the doubly-nested loop for covering each Δt sweep shown in Figure 14.3,

left-hand side.

474 14. Molecular Dynamics: Further Topics

Extrapolative MTS Impulse MTS

based on Position Verlet based on Velocity Verlet

≡ X +

Δt



slow

≡−M

−1

∇E

slow

(X)



slow

≡−M

−1

∇E

slow

) V ← V +

Δt



slow

For j =1 to k

For j =0 to k

− 1

≡ X

← X +

Δt



med

≡−M

−1

∇E

med

)



med

≡−M

−1

∇E

med

(X)



F ←



med



slow

V ← V +

Δt



med

For i =1 to k

For i =0 to k

− 1

X ← X +

Δτ

V V ← V +

Δτ



fast

V ← V +Δτ (



F +



fast

) X ← X +ΔτV

X ← X +

Δτ

V V ← V +

Δτ



fast

End End

V ← V +

Δt



med

End End

V ← V +

Δt



slow

Figure 14.3. Algorithmic sketches of molecular dynamics integration by two force-splitting

variants: extrapolation (left) versus impulses (right), based on position Verlet (extrapola-

tion) and velocity Verlet (impulses).

Note that in this loop the slow force is evaluated once (at the point X

), the

medium force is evaluated k

times (for each X

), and the fast force is evalu-

ated k

(or r) times at a corresponding midpoint. If the slow force calculations

take the majority of the CPU time, the MTS approach will result in signiﬁcant

computational savings.

In practical implementations, the force distance classes are best treated by a

smooth force-switching approach; see Chapter 10, Spherical-Cutoff section.

Simple extrapolation formulations, as above, were ﬁrst tried for molecu-

lar dynamics [486, 1231, 1232, 1243, 1279]. However, these variants exhibited

systematic energy drifts, a result of their nonsymplecticness.

14.3.3 Impulses

Work continued in the 1980s on MTS methods in a variety of contexts [1276,

1278], leading to the introduction in 1991/1992 (by Schulten and coworkers [486]

and independently by Berne and coworkers [1277]) to an MTS method which

14.3. Multiple-Timestep (MTS) Methods 475

is symplectic and time-reversible. This similar MTS variant, based on impulses

rather than extrapolation, was termed Verlet-I by the former group [486]and

r-Respa [1277] by the latter.

The reversible Respa method was derived from a general Trotter factorization

associated with the Liouville operator L. Liouville operators are fundamental

tools in statistical mechanics for the description of the canonical equations of

motion of Hamiltonian systems. The Liouville operator can be decomposed into

parts corresponding to different components of the energy using the reversible

Trotter factorization. Here, we write the Liouville operator Las a sum of three op-

erators that characterize the scales of motions associated with different potential

components:

L = L

fast

+ L

med

+ L

slow

We then use a symmetric factorization of the components to arrive at (recall that

Δτ =Δt

and k

Δt

=Δt):

exp [iΔtL]=exp[iΔt(L

fast

+ L

med

+ L

slow

)]

=exp





Δt



slow





exp





Δt



med



(exp [iΔτL

fast

])

exp





Δt



med



× exp





Δt



slow



+ O(Δt

This factorization effectively shows that the propagation of the solution can be

approximated by a combination of terms corresponding to several force com-

ponents, each of which is resolved on a suitable timescale (e.g., Δτ/Δt

/Δt

for fast/medium/slow components). The middle term, corresponding to the fast

components of the motion, is discretized with the Verlet method at a small

timestep (Δτ).

A sweep over one Δt interval by an impulse-MTS Verlet approach, based on

the leapfrog or velocity Verlet triplet (eq. 13.14), can be written as the doubly-

nested iteration process shown in Figure 14.3, right-hand side.

14.3.4 Vulnerability of Impulse Splitting to Resonance Artifacts

Note that the application of the slow force results in an impulse. The velocities are

modiﬁed only outside of the inner loop (i.e., at the onset and at the end of a sweep

covering Δt) by a term proportional to r Δτ, thus r times larger than the changes

made to X and V in the inner loop. This is shown schematically in Figure 14.4

for a dual-timestep method with r =4(see tall spikes at bottom).

Thus, as the time interval between slow-force updates increases, the size of

these “impulses” grows. This causes a resonance artifact when the impulse fre-

quency, or the MTS outer timestep Δt, occurs near a natural frequency of the

476 14. Molecular Dynamics: Further Topics

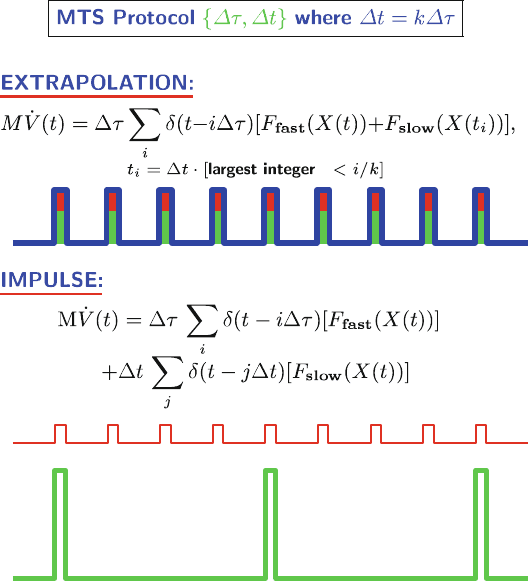
Figure 14.4. Schematic illustration of extrapolative vs. impulse force splitting integration

for a dual-timestep protocol with inner timestep Δτ and outer timestep Δt = kΔτ (k =4

used). In extrapolative splitting, a slow-force contribution (green) is made each time the

fast force (red) is evaluated (i.e., every Δτ interval). In impulse splitting, in contrast, con-

tributions of the slow forces (tall spikes) are considered only at the time of their evaluation

(e.g., every four fast-force evaluations).

system. This artifact results because the long-range forces add energy at pulses

that correspond to the natural frequency of the system. Of course, the true phys-

ical system experiences continuous variation of the long-range forces. Next we

analyze resonance artifacts of MTS methods in more detail for a harmonic model.

14.3.5 Resonance Artifacts in MTS

Analysis of a simple linear system is instructive to illustrate resonance in MTS

schemes [94,446]. Recent works [94,1024,1089] have shown that impulse meth-

ods are generally stable except at integer multiples of half the period of the

fastest motion, with the severity of the instability worsening with the timestep.

14.3. Multiple-Timestep (MTS) Methods 477

Extrapolation methods are generally unstable for the Newtonian model problem,

but the instability is bounded for increasing timesteps. Similar results hold for

stochastic extensions of MTS [94].

Simple Example

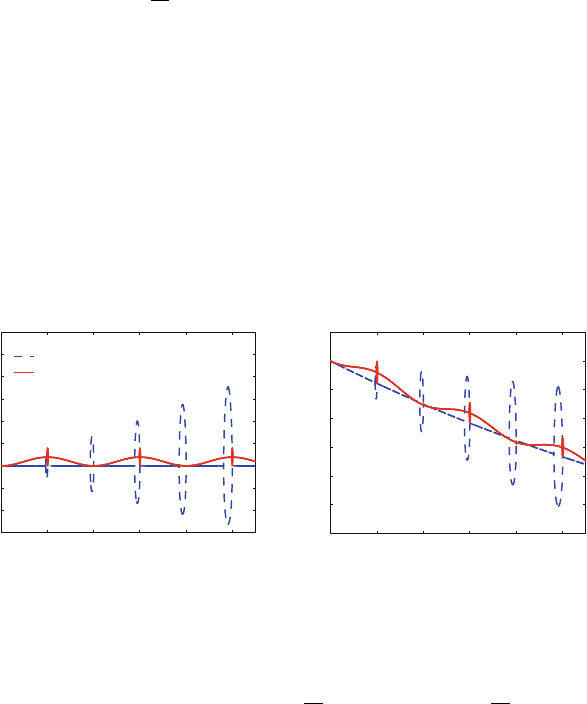
Figure 14.5 from [1089] illustrates this behavior as analyzed on a one-dimensional

linear oscillator obeying the equations

X = V,

V = −(λ

+ λ

)X,

where X and V denote the scalar position and velocity, respectively, and a unit

mass for the particle is assumed. The scalars λ

>λ

represent two motion com-

ponents differing in timescales. The characteristic angular frequencies associated

with these components and respective periods are



=2π/ω

,i=1, 2 .

For the analysis of Figure 14.5,wesetλ

= π

and λ

=(π/5)

to produce

=10=5T

time units. The slow force component is deﬁned as −λ

X and

is updated at timesteps Δt that are k times larger than those (Δτ)usedforthefast

components, −λ

In the linear analysis of [1089], eigenvalue magnitudes derived from the prop-

agation matrices associated with the impulse and extrapolation force splitting

schemes are plotted against the outer timestep. A scheme is unstable if the eigen-

value magnitude exceeds unity. Figure 14.5 shows results for both Newtonian

(left) and Langevin (right) dynamics; the latter, stochastic dynamics approach is

described in more detail below. The inner timestep was set to Δτ =0.001 and

the outer timestep to kΔτ (compare to T

=2and T

=10).

0 1 2 3 4 5

0.7

1.0

1.3

1.6

Δt

Eig. Magnitude

Impulse Verlet

Constant Ex.

Eig. Magnitude

0 1 2 3 4 5

0.4

0.5

0.6

0.7

0.8

0.9

1.1

Δt

Figure 14.5. Propagation-matrix eigenvalue magnitudes for Newtonian (left) and Langevin

(right, γ =0.162) impulse and extrapolative force-splitting methods as a function of

the outer timestep as calculated for a one-dimensional linear test system governed by

X = −(λ

+ λ

)X with λ

= π

, λ

=(π/5)

,whereX denotes the scalar posi-

tion of the particle with unit mass. These settings produce associated characteristic periods

for the fast and slow components of T

=2π/

√

=2and T

=2π/

√

=10time

units. The inner timestep is Δτ =0.001 [1089].

478 14. Molecular Dynamics: Further Topics

We see that the impulse method (dashed line) is unstable at integral multiples

(m) of half the fast period (mT

/2,whereT

/2=1here). Furthermore, the

severity of these corruptions increases with k, with the amplitudes of the resonant

spikes increasing linearly with Δt and becoming wider.

While the use of impulses clearly leads to serious artifacts at certain timesteps,

for other timesteps the impulse method is stable for this one-dimensional linear

model. It might seem that avoiding the resonant timesteps is possible in practice.

Unfortunately, experiments on a large nonlinear system show that once a resonant

timestep is reached, good numerical behavior cannot be restored by increasing the

timestep [1126]. See Figure 14.7 for an illustration of resonance on a nonlinear

system.

For the extrapolation method, in contrast, we note in Figure 14.5 (solid

curves) deviations from unit eigenvalues except around isolated outer timesteps.

Since both eigenvalues exceed one in magnitude, the method is not volume-

preserving or symplectic, explaining the energy drift observed in practice for force

splitting by extrapolation. Still, the resonant spikes for constant extrapolation

have magnitudes that are independent of the outer timestep, of values approxi-

mately 1+λ

/λ

(λ

/λ

=0.04 here). Therefore, the larger the separation of

frequencies, the more benign the numerical artifacts in practice.

Extensions to Stochasticity and Nonlinearity

These resonance patterns generalize to stochastic dynamics, where friction and

random terms are added (see next section), as seen in the same ﬁgure (the eigen-

value magnitudes decrease due to frictional damping). The value of γ used here

ensures that the ﬁrst spike for the impulse method has magnitude less than unity

[1089]. Behavior is more complicated for a linear three-dimensional test prob-

lem [1089]. Still, applications to a nonlinear potential function for a protein,

asshowninFigure14.7 (discussed below), exhibit similar overall patterns for

impulse versus extrapolative force splitting treatments.

14.3.6 Limitations of Resonance Artifacts

on Speedup; Possible Cures

The original work of Schulten and coworkers [486] expressed reservations regard-

ing force impulses. A subsequent study by Biesiadecki and Skeel [134] discussed

resonance as well as the systematic drift of extrapolative treatment in simple os-

cillator systems, though it conjectured that resonance artifacts were not likely to

be so clear in nonlinear systems. This, unfortunately, turned out not to be true.

Other articles noted a rapid energy growth [1349, 1448] when the interval be-

tween slow-force updates approaches and exceeds 5 fs, half the period of the

fastest oscillations in biomolecules

The presence of these resonances in impulse splitting limits the outermost

timestep, Δt (or the interval of slow-force update), in MTS schemes. In turn,

the overall speedup over a standard Verlet trajectory is capped. The achievable

14.4. Langevin Dynamics 479

speedup factor has been reported to be around 4–6 [1277, 1349, 1448]for

biomolecules. However, this number depends critically on the reference STS

(single-timestep) method to which MTS performanceis compared. Since the inner

timestep in MTS schemes is often small (e.g., 0.5 or even 0.25 fs), such speedup

factors around 5 are obtained with respect to STS trajectories at 0.5 fs (10 with

respect to 0.25 fs!). While accuracy is comparable when this small timestep is

used, typically STS methods use larger timesteps, such as 1 or 2 fs (often with

SHAKE). This means that the actual computational beneﬁt from the use of MTS

schemes in terms of CPU time per nanosecond, for example, is much less. Still,

a careful MTS implementation with inner timestep Δτ =0.5 fs can yield better

accuracy than a STS method using 1 or 2 fs.

Given this resonance limitation on speedup, it is thus of great interest to revise

these methods to yield larger speedups.

The molliﬁed impulse method of Skeel and coworkers [446, 594, 595]has

extended the outer timestep by roughly a factor of 1.5 (e.g., to 8 fs). With addi-

tional Langevin coupling, following the LN approach [95], the Langevin molliﬁed

method (termed LM) can compensate for the inaccuracies due to the use of im-

pulses to approximate a slowly varying force. This is accomplished by substituting

A(X)

slow

(A(X)) for the slow force term where A(X) is a time-averaging

function.

Another approach altogether is to use extrapolation in the context of a stochas-

tic formulation, as in the LN method [93–95] (see next section). This combination

avoids the systematic energy drift, alleviates severe resonance, and allows much

longer outer timesteps; see also discussion of masking resonances via the

introduction of stochasticity in an editorial overview [665] and review [328].

Though the Newtonian description is naturally altered, the stochastic formu-

lation may be useful for enhanced sampling. The contribution of the stochastic

terms can also be made as small as possible, just to ensure stability [99, 1109].

For example, unlike the predictions in the above review [328], a smaller stochas-

tic contribution (damping constant of 5 to 10 ps

−1

) has been used in the LN

scheme without reducing the outer timestep, and hence without compromising

the speedup [1230].

14.4 Langevin Dynamics

14.4.1 Many Uses

A stochastic alternative to Newtonian dynamics, namely Langevin dynamics, has

been used in a variety of biomolecular simulation contexts for various numeri-

cal and physical reasons. The Langevin model has been employed to eliminate

explicit representation of water molecules [966], treat droplet surface effects

[180,1189], represent hydration shell models in large systems [112–114], enhance

sampling [298, 328, 513, 659, 783, 1036, 1428], and counteract numerical damp-

ing while masking mild instabilities of certain long-timestep approaches [95,992,

480 14. Molecular Dynamics: Further Topics

1132,1435, 1436]. See Pastor’s comprehensive review on the use of the Langevin

equation [966]. The Langevin equation is also discussed in Subsection 10.6.3 of

Chapter 10 in connection with continuum solvation representations.

14.4.2 Phenomenological Heat Bath

The Langevin model is phenomenological [853] — adding friction and random

forces to the systematic forces — but with the physical motivation to represent a

simple heat bath for the macromolecule by accounting for molecular collisions.

The continuous form of the simplest Langevin equation is given by:

X(t)=−∇E(X(t)) − γM

X(t)+R(t), (14.27)

where γ is the collision parameter (in reciprocal units of time), also known as the

damping constant. The random-force vector R is a stationary Gaussian process

with statistical properties given by:

R(t) =0, R(t)R(t



)

 =2γk

TM δ(t −t



), (14.28)

where k

is the Boltzmann constant, T is the target temperature, and δ is the usual

Dirac symbol.

14.4.3 The Effect of γ

The magnitude of γ determines the relative strength of the inertial forces with

respect to the random (external) forces. Thus, as γ increases, we span the inertial

to the diffusive (Brownian) regime. The Brownian range is used (with suitable

algorithms) to explore conﬁguration spaces of ﬂoppy systems efﬁciently. See

[607, 1321], for instance, for applications to the large-scale opening/closing lid

motion of the enzyme triosephosphate isomerase (TIM), and to the juxtaposition

of linearly-distant segments in long DNA systems, respectively.

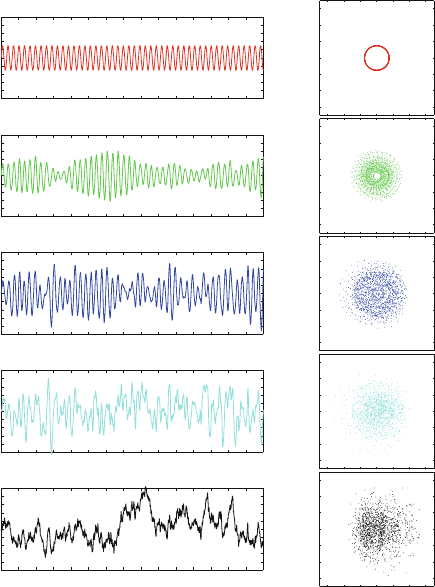
Figure 14.6 illustrates the effects of increasing γ on the trajectories and

phase diagrams of a harmonic oscillator. The systematic harmonic motion and

the closed, circular trajectories characteristic at zero viscosity change as the

relative contribution of the random to systematic forces increases.

Since the stochastic Langevin forces mimic collisions between solvent mole-

cules and the biomolecule (the solute), we see that the characteristic vibrational

frequencies of a molecule in vacuum are damped. In particular, the low-

frequency vibrational modes are overdamped, and various correlation functions

are smoothed (see Case [202] for a review and further references). The magnitude

of such disturbances with respect to Newtonian behavior depends on γ [95].

A physical value for γ for each particle can be chosen according to Stokes’ law

for a hydrodynamic particle of radius a:

γ =6πηa/m , (14.29)

where m is the particle’s mass (not to be confused with the integer m used to

deﬁne resonance), and η is the solvent viscosity. For example, γ =50ps

−1

is a

14.4. Langevin Dynamics 481

−.4

−.2

−.4

−.2

−.4

−.2

−.4

−.2

0 1000 2000 3000

−.4

−.2

γ =0

γ = 0.01

γ = 0.1

γ =1

−.7 0 .7

−.7

γ = 10

Figure 14.6. Langevin trajectories for a harmonic oscillator of angular frequency ω =1

and unit mass simulated by a Verlet extension to Langevin dynamics at a timestep of 0.1

(about 1/60 the period) for various γ. Shown for each γ are plots for position versus time

(left panels) and phase-space diagrams (right squares). Note that points in the phase-space

diagrams are not connected and only appear connected for γ =0because of the closed

orbit.

typical collision frequency for protein atoms exposed to solvent having a viscosity

of 1 cp at room temperature [967]; this value is also in the range of that estimated

for water (γ =54.9 ps

−1

It is also possible to choose an appropriate value for γ for a system modeled by

the simple Langevin equation so as to reproduce observed experimental trans-

lation diffusion constants, D

. Namely, in the diffusive limit, D

is related to

γ by

= k



mγ .

See [966, 1037] for example, for the use of these relations in studies of

supercoiled DNA.