Щелкачев В.Н. Основы и приложения теории неустановившейся фильтрации: Часть 1
Подождите немного. Документ загружается.


Развитию теории СКИП-функций, их табулированию и прило
жениям были посвящены работы В. Н. Белова [63], [64], В. А. Бер
куна [66], [67], В. С. Блинова [74], Ш. А. Гаджиева [151], А. Б. Зо
лотухина [293], 3. Ф. Карпычевой [332], О. Н. Харина и В. С. Бли
нова [636], В. Н. Щелкачева [756], [764], [755], [762], [752].
Выше цитировались работы, в которых приток жидкости к
окружной галерее рассматривался в условиях бесконечного пласта
В статье В. Н. Щелкачева, В. Е. Влюшина и О. Н. Харина [747],
опубликованной в 1964 г., была решена задача о притоке жидкости
к окружной галерее в условиях ограниченного по простиранию
пласта, причем как открытого, так и закрытого (т.е. когда граница
пласта служит контуром питания или когда нет притока жидкости
через нее); дебит галереи принимался постоянным.
В 1965 г. была опубликована еще более общая статья В. Е. Влю
шина и О. Н. Харина [140] о притоке жидкости к окружной галерее
в ограниченном по простиранию пласте, но дебит скважины принят
переменным — линейно зависящим от времени.
Результаты, полученные в этих двух статьях, изложены в § 2
и 3 главы 15.
§ 4. Непрерывно действующий поверхностный
сферический сток
Воспользуемся сначала методом интегрирования по времени
стокообразных решений. Именно используя формулу Томсона (8.28)
для определения понижения давления после пуска мгновенного
поверхностного сферического стока, выведем из нее формулу
понижения давления после пуска непрерывно действующего по
верхностного сферического стока с постоянным дебитом Qcф.
Рассуждая так же, как это было пояснено в главе 4 при
использовании метода интегрирования по времени стокообразных
решений, допустим, что в момент t - t f был включен поверхностный
сферический сток, действовавший с дебитом Qcф в течение малого
промежутка времени dt\ Полагая радиус сферы равным R и
пользуясь формулой (8.28), малое понижение давления d (Ар) за
время dt' в любой точке, отстоящей на расстоянии r<R от центра
сферы, получим в таком виде:

Интегрируя равенство (10.121) по времени, определяем пони
жение давления А р т внутри сферы в момент t
Л
_____
Q сф
____
Р1~ Р*
(*-'Г
4к (f-Г)
_ <R+r)‘
г 4к (f-Г)
dt'
. (10.122)
В 1-ом интеграле, входящем в формулу (10.122), сделаем замену
переменной; положим:
и =
R -r
V4 к (t - 1') '
(10.123)
Тогда получим:
(R -r) 1
'4k« - D
dt =
R -r fe -“
^lt—t' “* Vk J u2
R-r
2 VicF
du.
(10.124)
Для вычисления полученного интеграла воспользуемся способом
интегрирования по частям и учтем равенства (П. 17) и (П. 33),
определяющие дополнительную функцию ошибок и интегральную
дополнительную функцию ошибок:
R-r
тШ
R ~r_
27к?
R-r
2 VicF
(10.125)
2 V k 7 j— „ R -r 2 ^ K t n . ^ R -r
= л 3 7 ' -'п‘ е*с г Ш = П С ^ ,а*с гШ -
Примечание. Заметим, попутно, что равенство ( 1 0 . 1 2 5 ) можно
рассматривать и как формулу для определения интегральной
дополнительной функции ошибок:
оо j

Выполняя при вычислении второго интеграла, входящего в
формулу (10.122), те хе действия, какие были использованы в
равенствах (10.124) и (10.125), в итоге получаем, заменяя произве-
о * к
дение кр через —:
f . R-r . . /?+г
1е*с г Ш - 1ет{сг Ш
r<R.
(10.127)
Для точек вне сферы, т.е. для случая r>R, вывод формулы
был бы аналогичный, но только в равенстве (10.123) (а поэтому и
в окончательной формуле) надо переставить местами величины R
и г. Таким образом, понижение давления Ар Е (г, t) вне или на
поверхности сферы определяется формулой
A pE(r,t) = &b
h VkF
4 nRrk
. , r-R . , r+R
ierfc2lТ Г 1ефг Ш
r>R.
(10.128)
Формулы (10.127) и (10.128) определяют понижение давления
в любой момент времени в любой точке внутри, на или снаружи
поверхностного сферического стока, включенного в начальный
момент времени с постоянным дебитом.
Конечно, можно было бы рассмотреть более общий случай,
когда дебит сферического стока Q«j, не постоянный, а пере
менный и выражающийся, например, с помощью одночленной
степенной функции времени, как в равенстве (10.33). В случае
переменного дебита величину надо было бы внести в
(10.122) под знак интеграла. Окончательные расчетные формулы
для этого случая становятся несколько более сложными и здесь
не приводятся. Соответствующее исследование было проведено
в кандидатской диссертации У Сейн Мьинта [594] — бывшего
аспиранта кафедры теоретической механики Московского инсти
тута нефти и газа.
Заметим, что для получения выведенных формул (10.127) и
(10.128) вместо метода интегрирования по времени стокообраз
ного решения можно воспользоваться операционным методом.
Для этого надо использовать такие два дифференциальных
уравнения пьезопроводности для условий сферического радиаль
ного потока:

Э2Др/ 2bPl \ dbpi
дг2 г дг " к df ’ ,> 0 - (Ю.129)
Э2Ард 2 1 ЭАр£
Эг2 г Эг " к df ’ Г>* ’ ,> 0 - (Ю.130)
Применительно к рассматриваемой задаче, связанной с пуском
в начальный момент поверхностного сферического стока с посто
янным дебитом Qcф, должны удовлетворяться еще следующие
условия:
Ар г=Ар Е = 0 при t = 0, r*R, (10.131)
Ар/*<х> при г = 0, 0<t<<x>, (10.132)
Ар е = 0 при г = оо, 0<t<°of (10.133)
Ар/=АрЕ яри г = R, 0<t<oo, (10.134)
\L I Эг Эг
= 0 сф - C°nst, 0<t<oo .
(10.135)
Как и в предшествующем параграфе, подвергнем уравнения
(10.129) и (10.130) преобразованию Лапласа, учитывая условие
(10.131):
d2 АР/ 2 dAPj (10.136)
j i + j — АР j ,
dr2 r dr к
d2APE 2 dPE s A jy
dr2 * r dr к (10.137)
Решения этих обыкновенных дифференциальных уравнений
можно представить в таком виде:

VTr
e e K
APi-A j - +B i ~ ,
V|r -V^r
в С
A Pe = A 2^ - + B2E—^— .
С учетом (10.132) и (10.133) должно быть:
В 1——A j ; А 2 = 0.
(10.138)
(10.139)
(10.140)
Для определения коэффициентов А\ и В2 имеем еще два
условия (10.134) и (10.135); используя их, находим:
=
_______
е
1 SnRks*
B2~8KRks*ye "* У
(10.141)
(10.142)
Подставляя найденные значения коэффициентов Аи Bh Аъ В2
в равенства (10.138) и (10.139), получаем:
ЛР ОсфцУкг -У£(*-г> -УГ(д+о-| 1
8яЛгА: L * -1Я** (10.143)
лр бсфЦУк Г -У|Г<г-*) -V£<r+*)]J_
(10.144)
Для перехода от изображений к оригиналам воспользуемся
формулой (9.26), в которой примем п = 0:
-1
-VT.1
(10.145)
В итоге получаем те же формулы (10.127) и (10.128).
Понижение давления в центре сферы получаем, полагая в
формуле (10.127) г = 0 и раскрывая неопределенность по правилу
Лопиталя:

. , f tf * Q сфй . R (10.146)
Сравнивая эту формулу с формулой (4.15), легко убедиться в
том, что в центре поверхностного сферического стока понижение
давления оказывается таким, как если бы на расстоянии R от
центра был расположен непрерывно действующий точечный сток
с тем же дебитом, какой имеет сферический сток.
Полагая в формулах (10.127) и (10.128) г = R, определяем
понижение давления на поверхности сферы, учитывая соотноше
ние (П. 35):
(10.147)
Полагая в формуле (10.128) R =» 0 и раскрывая неопределен
ность по правилу Лопиталя, получаем:
An frtX Q^ arfr Т (Ш48>
APE(r,t)R=0 = j ^ e r f c j ^ T.
Формула (10.148) определяет понижение давления в любой
точке и в любой момент после пуска точечного стока (при R = 0
сфера обращается в точечный сток) в условиях сферического
радиального притока жидкости к нему. Естественно, что формула
(10.148) совпала с формулой (4.15).
Полагая в формулах (10.127), (10.128) * = <» и раскрывая
неопределенности, получаем:
Api(r’t) = f ^ R i ' r ~ R' t = °° (Ю.149)
а , бефМ- >JP , (Ю.150)
= rZR> t = °°■
Следовательно, процесс перераспределения давления заканчи
вается так, что понижение давления в центре сферы, во всех точках
внутри нее и на ее поверхности оказывается одинаковым, т.е. во
всех этих точках линии графиков понижения давления асимптоти
чески приближаются к горизонтальной прямой. Снаружи сферы

понижение давления в каждой точке асимптотически приближается
с течением времени к конечной величине, обратно пропорциональ
ной расстоянию г этой точки от центра сферы, как в этом убеждает
формула (10.150). Поэтому все пьезометрические линии, которые
можно в разные моменты построить для всех точек вдоль каждого
радиуса сферы, будут с течением времени опускаться, асимптоти
чески приближаясь к крайней пьезометрической кривой (соответ
ствующей значению t = 00) — к равносторонней гиперболе, опре
деляемой равенством (10.150).
Расход жидкости через поверхность сферического стока изнутри
при изменении времени от 0 до «> будет уменьшаться от ^ <2 сф
до 0. Поэтому углы наклона к горизонту касательных к пьезомет
рическим линиям при пересечении с прямой г = R изнутри сферы
с течением времени уменьшаются, стремясь к нулю. При t = co
расходы жидкости должны быть равны нулю через все сферические
поверхности, расположенные внутри сферического стока и ему
концентричные.
Наоборот, расход жидкости снаружи через поверхность сфе
рического стока будет при изменении времени от 0 до «э
увеличиваться от - Q сф до ()Сф. Поэтому соответствующие углы
наклона касательных к пьзометрическим кривым при их пере
сечении с прямой г = R снаружи сферы с течением времени
будут увеличиваться. При t = <» расходы жидкости через все
сферические поверхности, расположенные снаружи сферического
стока и ему концентричные, будут одинаковы и равны дебиту
стока
Чтобы в этом убедиться, учтем, что расход жидкости
Q(r, t ) в любой момент t через любую сферическую поверхность
радиуса г снаружи сферического стока и ему концентричную
определится так:
Ограничимся, например, моментом * = <». Продифференцируем
по г равенство (10.150) и значение производной подставим в
формулу (10.151):
Q(r,t) = -4nr
o k Э Ар (г, О
ц. Эг
(10.151)
Q{r,t) = -4 n r2±
к Q сф Д
|А 4пкг2
V У
что и требовалось проверить.

С учетом выведенных формул (10.127), (10.128), (10.146)-
(10.150) и проведенного выше анализа на рис. 10.2 и 10.3
схематично построены графики понижения давления соответст
венно для точек внутри поверхностного сферического стока и
для точек снаружи него.
Все линии на рис. 10.2 имеют общую горизонтальную асимптоту,
параллельную оси абсцисс и удаленную от нее на расстояние ОА,
определяемое равенством:
ОА = [ Ар (г, t) ] =
(?сфН
4я kR
Линия, соответствующая графику понижения давления для
любой точки на поверхности сферического стока, в начальный
момент касается оси ординат на рис. 10.2 и 10.3. Эта линия
отмечена обозначением г = R, и она расположена на каждом
рисунке ниже всех остальных линий, т.к. в любой момент
времени понижение давления будет наибольшим в точках на
поверхности сферического стока. Все остальные линии на ри
сунках 10.2 и 10.3 в начальный момент касаются оси абсцисс,
но чем более удалена точка от стока (т.е. чем больше г
отличается от R), тем позднее начинается в ней заметное
понижение давления; этим и объясняется, что на рисунках
соответствующие линии кажутся касающимися оси абсцисс не
в начальный момент, а в более поздние моменты. Все эти линии
(за исключением той, которой соответствует значение г = R)
имеют точки перегиба. Чтобы определить положение точки
перегиба, следует согласно обычной методике дважды продиф
ференцировать по времени равенства (10.127) и (10.128) и
приравнять нулю вторую производную. Для простоты определим
момент £пер, соответствующий точке перегиба для графика из
менения давления в центре сферы. Для этого надо было
продифференцировать по времени более ж простое равенство
(10.146); *пеР имеет такое значение:
' пер-6 к-
(10.154)
На рис. 10.4 изображены последовательные положения пье
зометрических линий (сечений пьезометрических воронок депрес
сии) для точек вдоль любого радиуса сферы. Пунктирная прямая
LN параллельна оси ординат и удалена от нее на расстояние R,
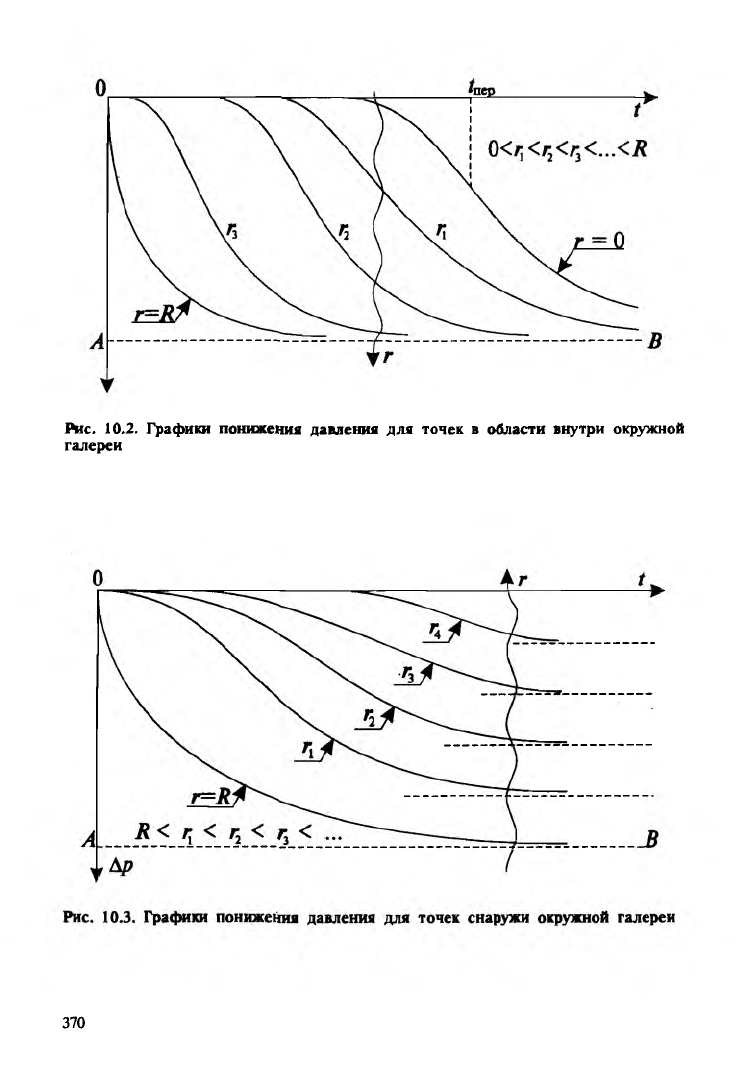
Рис. 10,2. Графики понижения давления для точек в области внутри окружной
галереи
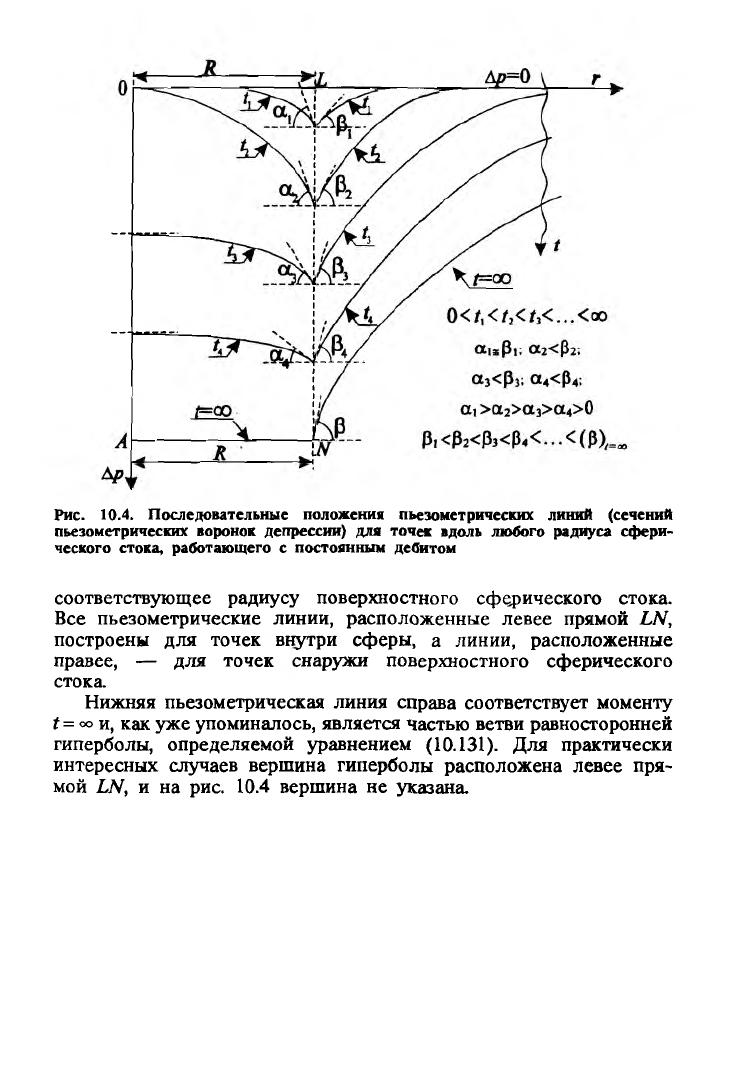
Рис. 10.4. Последовательные положения пьезометрических линий (сечений
пьезометрических воронок депрессии) для точек вдоль любого радиуса сфери
ческого стока, работающего с постоянным дебитом
соответствующее радиусу поверхностного сферического стока.
Все пьезометрические линии, расположенные левее прямой LN,
построены для точек внутри сферы, а линии, расположенные
правее, — для точек снаружи поверхностного сферического
стока.
Нижняя пьезометрическая линия справа соответствует моменту
t = оо и, как уже упоминалось, является частью ветви равносторонней
гиперболы, определяемой уравнением (10.131). Для практически
интересных случаев вершина гиперболы расположена левее пря
мой ZJV, и на рис. 10.4 вершина не указана.
