Щелкачев В.Н. Основы и приложения теории неустановившейся фильтрации: Часть 1
Подождите немного. Документ загружается.


где Г — символ гамма-функции — см. § 1 Приложения. В рассмат
риваемом случае для ВГФ, входящей в знаменатель формулы (5.54),
надо принять, что
поэтому с i< l при а = 0,1,2, 3,... Учитывая соотношение (5.55),
формулу (5.54) можно переписать так:
Формула (5.56) совпадает с формулой (4.125). В главе 4 формула
(4.125) и все остальные были выведены с помощью «метода
интегрирования стокообразных решений», а здесь формула (5.56)
была выведена сведением задачи интегрирования дифференциаль
ного уравнения расхода к стандартной процедуре интегрирования
вырожденного гипергеометрического уравнения.
Совершенно аналогичным приемом можно было бы и задачу
интегрирования дифференциального уравнения пьезопроводности
также свести к стандартной процедуре интегрирования вырожден
ного гипергеометрического уравнения, причем в результате
получили бы формулу (4.119) или (4.120), но выведенную иным
методом. j
Приведенные рассуждения доказывают, что исследования од
номерных потоков можно проводить разными методами, причем в
дальнейшем будет еще указан и метод, связанный с использованием
операционного исчисления (см., например, главы 9 и 10).
4' s +
ч
/
1 - а 1 - а £_) (5.56)
2 * 2 ’ 4Kt *
У
V У

РЕШЕНИЕ КЛАССИЧЕСКИМИ МЕТОДАМИ АВТОМОДЕЛЬНЫХ ЗАДАЧ,
СВЯЗАННЫХ С ИССЛЕДОВАНИЕМ ПРОСТЕЙШИХ НЕУСТАНОВИВШИХСЯ
ОДНОМЕРНЫХ ПОТОКОВ
§ 1. Напоминание условий автомодельности задач и метода
Коши для их решения
В данной главе исследования простейших одномерных потоков
будут проводиться так, как это обычно принято при решении
автомодельных задач с использованием метода Коши.
Сначала напомним то определение автомодельности задач,
которое достаточно для данной работы — см., например, [553], [425].
Задача автомодельна (самоподобна), если в ее условия не входят
никакие характерные (избранные) линейные или временные вели
чины, а число размерных определяющих параметров должно быть
не более двух, причем с независимыми размерностями, отличными
от длины и времени. Смысл самого термина «автомодельность»
(самоподобие) будет пояснен в этом же параграфе, но дальше.
При решении автомодельной задачи по методу Коши диффе
ренциальное уравнение в частных производных сводится к решению
обыкновенного дифференциального уравнения для функции, ар
гумент которой представляет собой безразмерную комбинацию
величин, входящих в постановку задачи.
Рассмотрим задачу, которая, как это будет очевидно, удовлет
воряет условиям автомодельности.
Дифференциальные уравнения (5.7) и (5.8) для прямолинейно
параллельных потоков могут быть записаны в такой единой форме:
Э2Ф ( и > _ 1 ЭФ (3.0
Э|2 к Э t
(6.1)
где
Ф (|,f)«A/>
(6.2)
для дифференциального уравнения пьезопроводности и
ф ( !.п - е *
(6.3)
для дифференциального уравнения расхода

Считая поток в начальный момент t = 0 невозмущенным,
получаем следующее начальное условие:
[Ф (|.ОЬ«о*Ф (&0) = 0, 0<|<°о.
(6.4)
В качестве второго условия (граничного) примем
[ Ф ( ^ О ] |=о = Ф ( О» О = cons*- С* 0 < t < оо. (6.5)
Физический смысл граничного условия (6.5) состоит в том, что,
начиная с момента t = 0, на плоскости ^ = 0, т.е. на стенке
прямолинейной галереи, все время удерживается постоянным либо
понижение давления Ар, либо расход Q.
В математическую постановку данной задачи, связанной с
уравнением (6.1), начальным (6.4) и граничным (6.5) условиями,
входят только два размерных определяющих параметра: коэффи
циент пьезопроводности к и константа С. Величина к имеет
размерность L2T X\ константа С имеет размерность либо понижения
давления МЬЛТ2, либо размерность объемного расхода 1?ТХ.
Следовательно, сформулированная задача действительно удовлет
воряет требованиям автомодельности.
Величины, входящие в задачу, могут быть объединены в одну
I 2
безразмерную комбинацию “ или . Далее будет обнаружено,
что с помощью только одной такой безразмерной комбинации
могут быть охарактеризованы все особенности исследуемого не-
установившегося одномерного потока.
Впервые Копта ввел для решения задач такого типа безразмер
ную комбинацию величин и указал, что само решение задачи
следует искать в виде
где D — постоянная величина, а / — символ искомой функции*.
Постоянный множитель 4 под знаком корня не имеет существенного значения
и введен только для упрощения последующих выкладок.
(6.6)

Введем обозначение для безразмерной величины
w =i h i '
продифференцируем равенство (6.6):
Э! Ф D .
j » , _ _ O j , , (w ) <6 -8 >
Учитывая равенства (6.8) из уравнения (6.1), умножая обе его
AKt
части на — получаем:
/"(w) + 2w//(w) = 0. (6.9)
Итак, искомая функция f(w) может быть определена интегри
рованием обыкновенного линейного дифференциального уравне
ния (6.9) второго порядка с переменным коэффициентом.
Уравнение (6.9) совпадает с дифференциальным уравнением
(П. 43), которому удовлетворяет дополнительная функция ошибок
Хо(нО, т.е. erfc w; поэтому f(w ) = erfcw.
Свойства дополнительных функций ошибок описаны в § 2
Приложения.
Следовательно, равенство (6.6) можно переписать так:
(6.10)
По известному свойству дополнительной функции ошибок —
см. формулу (П. 24) — erfc > 0 при f-»0. Следовательно,
функция Ф(|,О» определяемая равенством (6.10), удовлетворяет
начальному условию (6.4).
Постоянную величину D определим из граничного условия (6.5).
Действительно, полагая | = 0 в формуле (6.10) и учитывая, что
erfc 0 = 1 — см. (П. 24), получаем
Ф(0,О = Я. (6.11)

Сравнивая равенства (6.5) и (6.11), обнаруживаем, что
D = C.
(6.12)
Будем считать, что уравнение (6.1) есть дифференциальное
уравнение пьезопроводности, т.е. будем еще учитывать равенство
(6.2) и физический смысл условия (6.5), согласно которому
константа С должна быть равна постоянному понижению давления
Ар с, установленному на стенке прямолинейной галереи. Тогда
вместо (6.6) получим следующее решение уравнения (6.1), т.е.
получим формулу для распределения понижения давления в
прямолинейно-параллельном потоке:
Как и следовало ожидать, формула (6.13) совпадает с формулой
(4.140) при учете еще равенства (4.144).
В другом варианте будем рассматривать уравнение (6.1) как
дифференциальное уравнение расхода, т.е. учтем равенство (6.3).
Тогда по физическому смыслу условия (6.5) константа С должна
быть равна постоянному расходу жидкости Qc через стенку
прямолинейной галереи. Поэтому вместо (6.6) получим решение
уравнения (6.1) в такой форме:
Формула (6.14) позволяет определить расход жидкости через
любое сечение £ = const прямолинейно-параллельного потока в
любой момент.
Если в формуле (6.14) принять % = 0, то получается, что
(G|)|=o = Qo как и наД° было ожидать. Следует учитывать, что
в рассматриваемой задаче под Qc подразумевается расход жидкости
только через одну стенку прямолинейной галереи, так как в условиях
полубесконечного пласта жидкость притекает к галерее только с
одной стороны (в условиях бесконечного пласта жидкость притекает
к галерее с двух сторон и тогда учитывается расход жидкости
через ее две взаимно противоположные стенки).
Как и следовало ожидать, формула (6.14) совпадает с формулой
(4.19), полученной в главе 4 в результате применения другого
(6.13)
(6.14)

метода, а именно метода интегрирования стокообразного решения*
Формула же (6,13) получена здесь классическим методом, который
впервые был использован Коши и который теперь является типовым
для решения автомодельной задачи интегрирования дифференци
ального уравнения (6.1) при условиях (6.4) и (6.5).
В выборе решения дифференциального уравнения (6.1) в
форме (6.6) важно отметить, что, как уже упоминалось, впервые
Коши использовал безразмерную комбинацию величин, которая
послужила новой независимой переменной, определяемой равен
ством (6.7). Именно это и дало возможность свести задачу
интегрирования дифференциального уравнения в частных про
изводных (6.1), в которое входили две независимые переменные
% и t, к интегрированию обыкновенного дифференциального
уравнения (6.9) только с одной независимой переменной w.
Поэтому нет никакого основания называть, как это делают
многие авторы, например Кранк [811], равенство (6.7) преобразо
ванием Больцмана. Действительно, Больцман широко использовал
преобразование (6.7) для сведения дифференциальных уравнений
в частных производных к обыкновенным дифференциальным
уравнениям. Однако соответствующая работа Больцмана была им
выполнена и опубликована в 1894 г., т.е. намного позднее исследо
ваний Коши, законченных в первой половине девятнадцатого века.
Описанное выше решение Коши можно, по-видимому, рассмат
ривать как первое (самое раннее) решение автомодельной задачи.
Сам термин «автомодельность» появился позже публикаций не
только Коши и Больцмана, но и позже работы Хартри [853],
анализируемой в следующем параграфе.
Заметим, что в теории фильтрации впервые Г. И. Баренблатт
[43], [44], [49] весьма плодотворно использовал метод решения
автомодельных задач, причем не только при интегрировании
линейных, но и нелинейных дифференциальных уравнений, свя
занных с движением газа в пористой среде. При интегрировании
такого типа линейного дифференциального уравнения теории
фильтрации, какой рассматривается в следующем параграфе,
Г. И. Баренблатт не знал, очевидно, работы Хартри [853] и поэтому
не использовал введенные им кратные интегральные дополнитель
ные функции ошибок (/п erfc).
Следует также заметить, что все использованные в главе 3
фундаментальные решения дифференциальных уравнений пьезоп
роводности можно было получить как решения соответствующих
автомодельных задач.
В § 4 главы 5 было упомянуто, что выбор решения дифферен
циального уравнения расхода (5.5) в форме (5.35) также был связан
с автомодельностью задачи, сформулированной в § 4 главы 5.
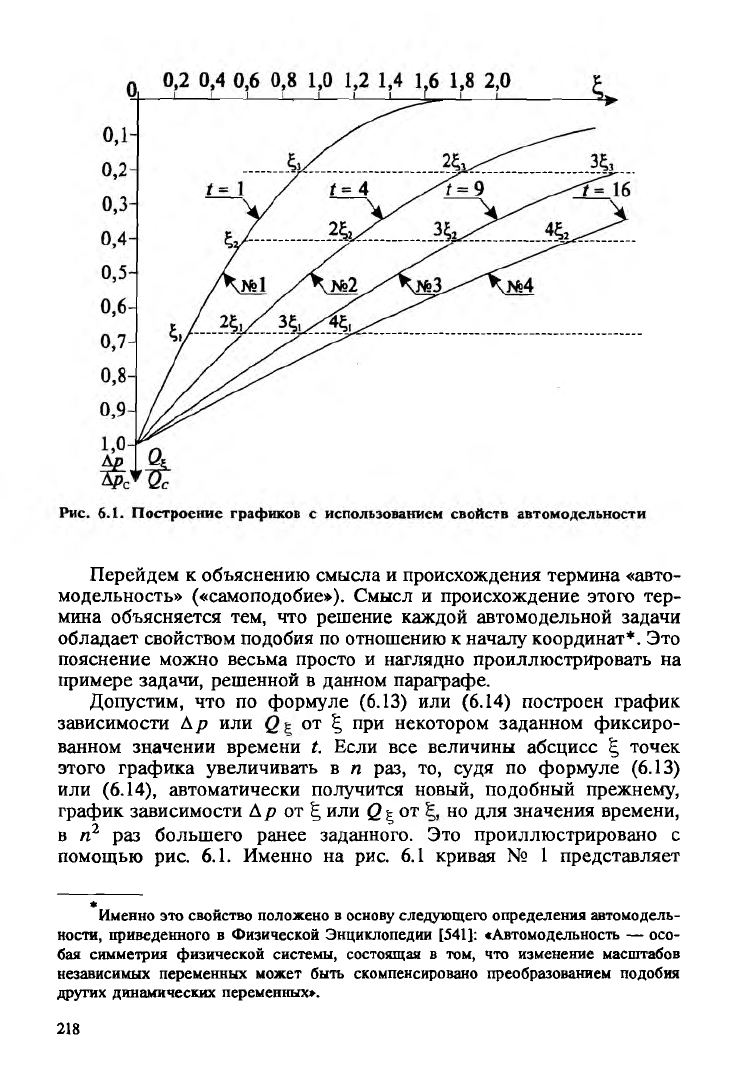
Перейдем к объяснению смысла и происхождения термина «авто
модельность» («самоподобие»). Смысл и происхождение этого тер
мина объясняется тем, что решение каждой автомодельной задачи
обладает свойством подобия по отношению к началу координат*. Это
пояснение можно весьма просто и наглядно проиллюстрировать на
примере задачи, решенной в данном параграфе.
Допустим, что по формуле (6.13) или (6.14) построен график
зависимости Ар или от | при некотором заданном фиксиро
ванном значении времени t Если все величины абсцисс ^ точек
этого графика увеличивать в п раз, то, судя по формуле (6.13)
или (6.14), автоматически получится новый, подобный прежнему,
график зависимости А р от ^ или Q ^ от но для значения времени,
в п2 раз большего ранее заданного. Это проиллюстрировано с
помощью рис. 6.1. Именно на рис. 6.1 кривая № 1 представляет
*
Именно это свойство положено в основу следующего определения автомодель
ности, приведенного в Физической Энциклопедии [541]: «Автомодельность — осо
бая симметрия физической системы, состоящая в том, что изменение масштабов
независимых переменных может быть скомпенсировано преобразованием подобия
других динамических переменных».

собой график зависимости величины —— или — построенный
А р с Q с
по формуле (6.13) или (6.14) с помощью таблицы значений
дополнительной функции ошибок
erfc. Основные свойства этой
функции приведены в § 2 Приложения, где также приведены
указания справочников с таблицами этой функции.
Предположим, что кривая № 1 представляет собой график, соот
ветствующий моменту t = 1. Учитывая свойство автомодельности,
совсем не требуется новых табличных данных для построения графи
ков при других значениях времени L Так, например, кривая № 2
построена удвоением абсцисс точек кривой № 1 и она соответствует
уже окончанию промежутка времени вчетверо большего, т.е. соот
ветствует моменту t = 4. Кривые № 3 и № 4 построены с помощью
увеличения абсцисс точек кривой № 1, соответственно в 3 и в 4 раза
Поэтому кривые № 3 и № 4 представляют собой графики изменения
рассматриваемых величин для моментов t = 9 и t = 16.
§ 2. Решение Хартри
для прямолинейно-параллельного потока
Допустим, что решение дифференциального уравнения (6.1)
имеет вид: *
(6-15)
где D — постоянная величина, п — любое целое положительное
или отрицательное число или нуль, fn — символ искомой функции,
выражение которой зависит от выбора числа л.
Дифференцируя равенство (6.15) по ^ и t, подставляя найденные
производные от функции Ф ( t ) в дифференциальное уравне
ние (6.1), получаем, учитывая равенство (6.7), такое обыкновенное
дифференциальное уравнение для определения искомой функции
f"n(w ) + 2w/'(w)-2n(w) = 0. (6.16)
Особая заслуга Хартри [853] состояла в том, что он определил
и впервые ввел в'употребление новые высшие трансцендентные
функции — кратные интегральные дополнительные функции оши
бок Perfc w, доказав, что они являются решениями уравнения (6.16).

Тем самым Хартри доказал, что введенные им новые функции
могут быть использованы для решения простейшего уравнения
«типа теплопроводности» (6.1)*.
Итак,
f n(w)=inerfcw. (6.17)
Определение и свойства кратных интегральных дополнительных
функций ошибок приведены в § 2 Приложения. Дифференциальное
уравнение (6.16) совпадает с дифференциальным уравнением
(П. 43).
При определении своих функций и при рассмотрении уравнения
(6.16) Хартри ограничился только положительными целыми зна
чениями числа /г.
Безразмерная комбинация величин в аргументе функции fn та
же, что и была в решении Коши (6.10), которое получается как
частный случай решения уравнения (6.15) при
п = 0.
С учетом равенств (6.15), (6.17) и (6.7) решение Хартри
дифференциального уравнения (6.1) для прямолинейно-параллель
ного потока примет такой вид:
Ф {%,t) = Dt"Ai nerfc ^ ^ j. <6Л8>
Если предположить, что уравнение (6.1) есть именно диффе
ренциальное уравнение пьезопроводности, то решение Хартри (6.18)
можно переписать так — см. равенство (6.2):
(6-19)
Имея формулу (6.19) для понижения давления и пользуясь
соотношением (П. 40), определяем расход жидкости Q ^ через
сечение потока £, = const площадью о:
Q = Л .а *ьр<.^Кв-*£-,»г-'еф -Л ~. (“ О)
6 ц bt jav4 k t V4k?
*
Если известно определяемое формулой (6.17) одно частное решение линейного
дифференциального уравнения (6.16) второго порядка, то можно по формуле Ост-
роградского-Лиувилля [565] найти второе независимое частное решение. Оно здесь
не приводится, так как в статье [755] было доказано, что оно не имеет физического
смысла. То же самое было доказано в главе 5 при анализе формулы (5.47), опреде
лявшей решение более общего обыкновенного дифференциального уравнения.

Определим еще объем жидкости V ^ которая за время t
перетекла через сечение потока % = const площадью о; этот объем
равен упругому запасу жидкости, которая за время t извлекается
через упомянутое сечение, т.е.
7 (6.21)
V ^ \ roA pd l,
где р * — коэффициент упругоемкости пласта.
Подставляя в формулу (6.21) выражение Ар из формулы (6.19)
и учитывая равенство (П. 29), получаем:
V4 = D$*o2&t'^n + l)in + l e r f c ^ ^ .
(6.22)
Полагая | = 0 и учитывая равенство (П. 36), из формул (6.19),
(6.20) и (6.22) находим выражения соответствующих величин
&Р с* Qc и Ус на стенке галереи:
<«)«— g . ( » ) - a. r [ l t "* .g . , ) l p g «lt<- > . < 6 •2 4 ,
(V)b-n = V (t)-
-------
^ Vk
-------
+ n
Л ) 2пГ[1 + И(л + 1)] ‘ (6.25)
Из формул (6.23)-(6.25) получается, что
А р C=D- const при л = 0, (6.26)
^ ™ к<* ^ 1 (6*27)
Qc-D^
----
г“ = const ПрИЛ*1,
2p,VK к
Ус = 2 Z? Р * c r = const при п - -1. (6.28)
