Щеглова И.Ю., Печенов В.В. Виртуальный физический практикум
Подождите немного. Документ загружается.


Изучение стабилизатора постоянного напряжения.
81
Отчет.
Отчет по работе должен содержать:
1. Схему установки для изучения проходной характеристики стабилизатора, выпол-
ненную в программе Electronics Workbench.
2. Таблицу с паспортными данными стабилитрона, а также параметрами стабилизато-
ра.
3. Таблицу с экспериментально определенными значениями входного и выходного
напряжения и проходную характеристику стабилизатора.
4. Расчет коэффициента стабилизации.
Примечание: Все данные сохранять в одной папке - Стабилитрон, которая создается до
начала работы.

Изучение свободных электрических колебаний в колебательном контуре.
82
Лабораторная работа № 2.6.
ИЗУЧЕНИЕ СВОБОДНЫХ КОЛЕБАНИЙ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ.
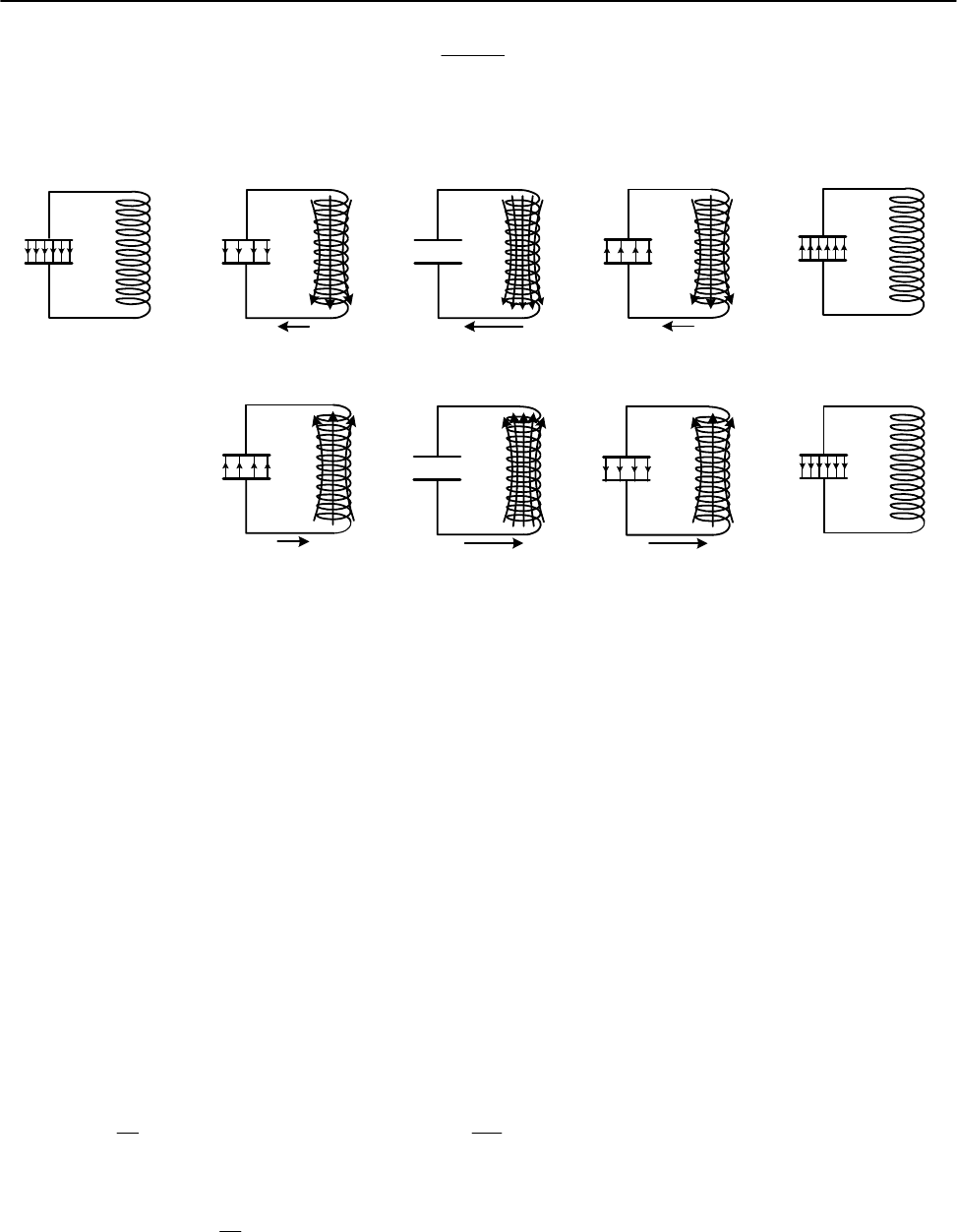
Рассмотрим электрическую цепь,
состоящую из последовательно соеди-
ненных конденсатора емкости С, ка-
тушки индуктивности L и сопротивле-
ния R (см. рис. 1). При определенных
условиях в такой цепи могут возникать
электрические колебания, т.е. периоди-
ческие изменения силы тока, заряда на
обкладках конденсатора и напряжения
на отдельных участках цепи.
C
R
L
Рис. 1. Простейший колебательный
контур.
Поэтому такую цепь называют электрическим колебательным контуром.
Вследствие наличия в цепи активного сопротивления, на котором происходит
выделение тепловой мощности, колебания будут с течением времени затухать,
причем тем быстрее, чем больше активное сопротивление.
Возбудить колебания в контуре можно, например, зарядив конденсатор.
После замыкания ключа конденсатор будет разряжаться, и в цепи возникает
электрический ток, однако он не сразу достигает своего максимального значе-
ния, т.к. этому препятствует явление самоиндукции. В результате ток увеличи-
вается постепенно и в тот момент, когда он достигает своего максимального
значения, заряд конденсатора обращается в нуль. Опять-таки из-за наличия в
цепи индуктивности ток не может исчезнуть сразу, а будет убывать постепенно,
перезаряжая конденсатор. Поэтому, когда ток в цепи станет равным нулю, кон-
денсатор вновь оказывается заряженным, но знаки заряда его обкладок будут
противоположны первоначальным. Затем процесс повторяется с той лишь раз-
ницей, что ток будет течь в противоположном направлении. Промежуток вре-
мени от начала разрядки конденсатора до его полной перезарядки (когда систе-
ма возвращается в исходное состояние) соответствует периоду колебаний. На
рис. 2 показан процесс возникновения электрических колебаний в простейшем
колебательном контуре без активного сопротивления.
В процессе колебаний энергия электрического поля конденсатора полно-
стью или частично переходит в энергию магнитного поля катушки. Так, напри-
мер, энергия изображенного на рис. 2 контура в начальный момент времени
(ток отсутствует) равна энергии электрического поля, сосредоточенного между
обкладками конденсатора:
C
q
WW
o
э
2
2
== . При наличии тока (моменты t
1
, t
3
, t
5
, t
7
– конденсатор частично разряжен) энергия контура складывается из энергии
электрического поля конденсатора и магнитного поля катушки:
22
22
LI
C
q
WWW
мэ
+=+=
. Наконец, когда ток в цепи достигает максимального
значения (конденсатор полностью разряжен), вся энергия целиком переходит в
Изучение свободных электрических колебаний в колебательном контуре.
83
энергию магнитного поля:
2
2
max
LI
WW
м
== . Поскольку в рассмотренной цепи не
происходит потерь на ленц-джоулево тепло, полная энергия, запасенная в кон-
туре (электрическая плюс магнитная), остается неизменной, и колебания будут
незатухающими.
C
L
+q
o
t
o
=0; I=0
C
L
+q
t
1
; I
C
L
t
2
=T
o
/4; I=I
max
C
L
t
3
; I
+q
C
+q
o
t
4
=T
o
/4; I=0
C
L
t
5
; -I
+q
C
L
t
6
=3T
o
/4; -I
max
C
L
+q
o
t
8
=T
o
; I=0
CL
t
7
; -I
+q
o
L
Рис. 2. Возникновение электрических колебаний в простейшем контуре без ак-
тивного сопротивления.
Включение в цепь активного сопротивления приводит к тому, что энергия
электромагнитного поля постепенно переходит во внутреннюю энергию про-
водника, в результате чего амплитуда колебаний с течением времени уменьша-
ется, - колебания затухают.
Рассмотренные колебания называются
свободными, или собственными,
т.к. они совершаются за счет первоначально сообщенной энергии при после-
дующем отсутствии внешних воздействий на колебательную систему (систе-
му, совершающую колебания), и могут быть, как мы видели, незатухающими и
затухающими.
Получить уравнение колебательного контура, приведенного на рисунке,
можно из следующих соображений: сумма падений напряжений на конденсато-
ре и активном сопротивлении в каждый момент времени должна быть равна
э.д.с. самоиндукции, возникающей в катушке.
cRC
UU E=+ ,
где
C
q
U
C
= , RIU
R
⋅
= ,
t
q
LIL
c
d
d
E −=
′
⋅−=
, а q и I – заряд конденсатора и ток в
цепи в некоторый момент времени (мгновенные значения). Отсюда
0=+⋅+
′
⋅
C
q
IRIL
.
Это и есть уравнение затухающих колебаний в колебательном контуре. Его
удобнее переписать следующим образом: поделим обе части равенства на ин-
дуктивность L и учтем, что ток – первая производная заряда по времени.

Изучение свободных электрических колебаний в колебательном контуре.
84
0
1
=+
′
+
′′
q
L
C
q
L
R
q или 0
1
d
d
d
d
2
2
=+⋅+ q
L
C
t
q
L
R
t
q
.
Введем обозначения:
L
R
=β2
, где
β
- коэффициент затухания, характеризую-
щий быстроту затухания колебаний (колебания затухают тем быстрее, чем
больше активное сопротивление и меньше индуктивность), и
L
C
o
1
2
=ω , где
o
ω
-
собственная циклическая частота колебаний. В результате уравнение колебаний
принимает вид:
02
2
=ω+
′
β+
′′
qqq
o
. (1)
Если в контуре отсутствует (в идеале) активное сопротивление или оно
пренебрежимо мало, колебания будут незатухающими. Уравнение таких коле-
баний имеет вид:
0
2
=ω+
′′
qq
o
. (2)
Решением этого уравнения является периодическая функция
()
ϕ
+
ω⋅= tqq
oo
cos , (3)
где q
o
– максимальное значение заряда на обкладках конденсатора (амплитуда
заряда); ϕ - начальная фаза колебаний;
(
)
ϕ
+
ω
t
o
- фаза колебаний в произволь-
ный момент времени t. Фаза колебания определяет значение колеблющейся ве-
личины в данный момент времени и показывает развитие процесса во времени.
Как видно из формулы, свободные незатухающие колебания являются гармо-
ническими, а, следовательно, периодическими. Это означает, что определенные
состояния системы, совершающей гармонические колебания, повторяются че-
рез промежуток времени Т
о
, называемый периодом свободных незатухающих
колебаний, за который фаза колебания получает приращение равное 2π. Период
незатухающих колебаний связан с собственной круговой частотой формулой:
LCT
o
o
π=
ω
π
= 2
2
, (4)
называемой формулой Томсона в честь английского физика В. Томсона, соз-
давшего теорию электрических колебаний в 1853 г.
Зная закон изменения заряда конденсатора, можно легко получить законы
изменения тока в контуре, а также напряжения на различных элементах этого
контура. Из теории колебательного контура, а также из простых рассуждений
(см. возникновение колебаний в контуре, рис. 2) следует, что колебания напря-
жения на резисторе совпадают по фазе с колебаниями тока в цепи; колебания
напряжения на индуктивности опережают по фазе колебания тока на π/2, а ко-
лебания напряжения на емкости, наоборот, отстают на π/2, что означает, что
ко-
лебания напряжения на индуктивности и емкости происходят в противофазе.
Если в контуре присутствует активное сопротивление, то колебания с те-
чением времени будут затухать (в действительности колебания всегда будут за-
тухающими, т.к. все проводники обладают сопротивлением). Уравнение зату-
хающих колебаний имеет вид (1). Амплитуда колебаний с течением времени
Изучение свободных электрических колебаний в колебательном контуре.
85
уменьшается до нуля и в этом смысле затухающие колебания нельзя назвать
периодическими, т.к. состояние системы никогда в точности не повторяется.
Однако, поскольку заряд на обкладках конденсатора достигает максимума (или
минимума), а также проходит через нулевое значение через равные промежутки
времени (периодически), эти колебания можно характеризовать некоторым ус-
ловным периодом, называемым периодом затухающих колебаний T. Ему соот-
ветствует частота колебаний ω, также отличающаяся от собственной цикличе-
ской частоты колебательного контура.
Затухание колебаний принято характеризовать, во-первых, коэффициен-
том затухания
L
R
2
=β , который показывает, как быстро происходит затухание
колебаний; и, во-вторых,
логарифмическим декрементом затухания λ, кото-
рый, по определению, представляет собой натуральный логарифм отношения
двух амплитуд, разделенных периодом:
)(A
)(A
ln
Tt
t
+
=λ
, (5)
и равен произведению коэффициента затухания на период (
T
β=λ
). В свою
очередь, это произведение есть величина, обратная числу полных колебаний
e
N
, совершаемых за время, в течение которого амплитуда убывает в е раз (е –
основание натурального логарифма е≈2,718).
Аналитическое решение уравнения (1) приводит к следующим выводам:
1. Частота затухающих колебаний
22
β−ω=ω
o
. Соответственно период
затухающих колебаний
() ()
2222
11
222
o
o
oo
o
T
T
ωβ−
=
ωβ−ω
π
=
β−ω
π
=
ω
π
=
, где
Т
о
– период собственных незатухающих колебаний.
2. Амплитуда затухающих колебаний с течением времени убывает по
экспоненциальному закону.
3. Колебания возникают только в том случае, когда 0
22
>β−ω
o
. Если
0
22
=β−ω
o
, процесс перестает быть колебательным и происходит апериодиче-
ский (т.е. непериодический) разряд конденсатора. Активное сопротивление
контура, при котором наблюдается прекращение колебаний, называется крити-
ческим. Получим выражение для критического сопротивления:
C
L
R
L
R
LC
кр
кр
o
2
4
1
;
2
2
22
=⇒=β=ω . (6)
Случай 0
22
<β−ω
o
также соответствует апериодическому процессу.
Уравнение затухающих колебаний можно решить не только аналитиче-
ски, но и численным методом, который является приближенным. Однако в дан-
ной работе для изучения затухающих колебаний мы воспользуемся программой
схемотехнического моделирования Electronics Workbench, с помощью которой
проверим некоторые выводы теории.
Изучение свободных электрических колебаний в колебательном контуре.
86
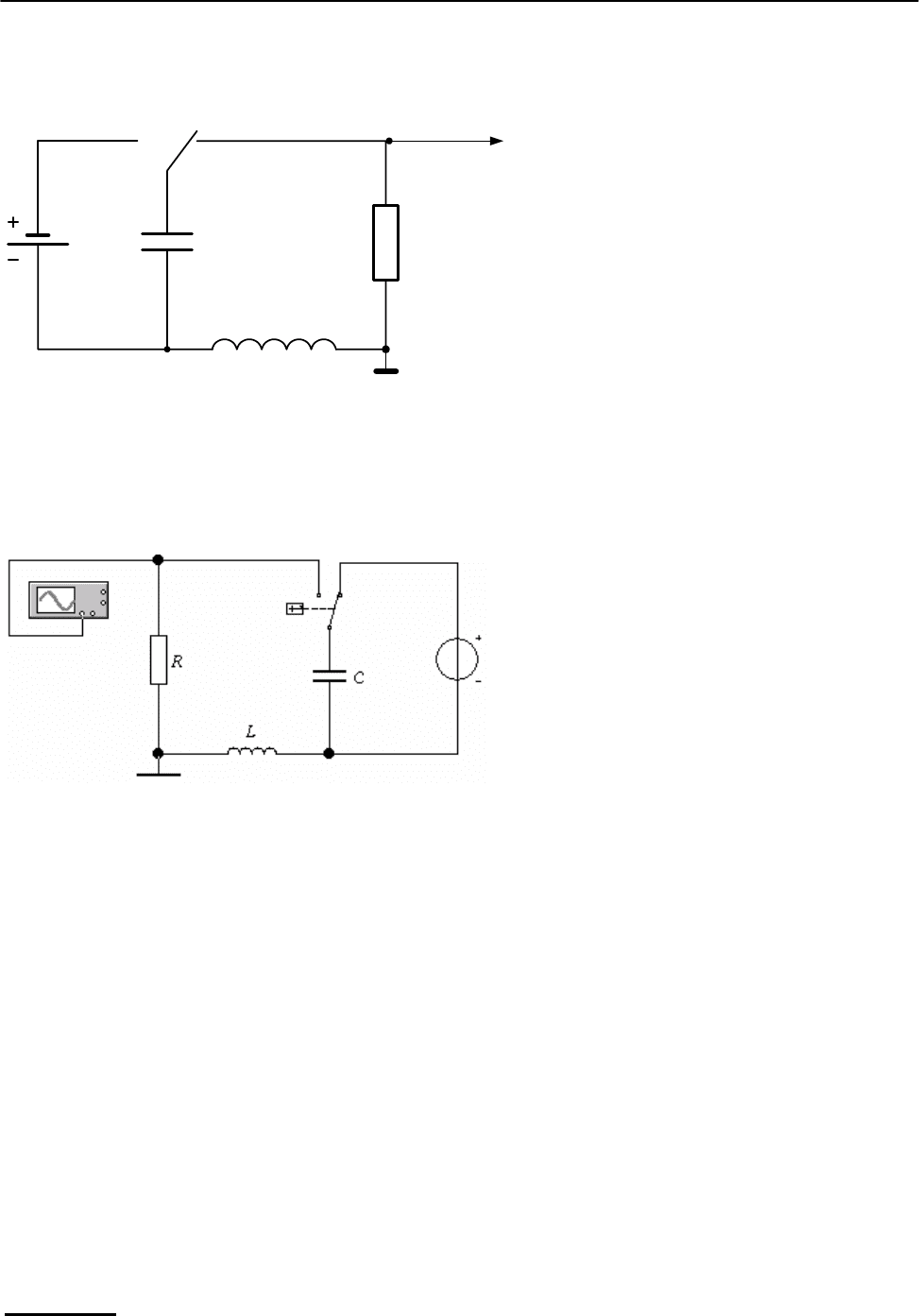
ОПИСАНИЕ УСТАНОВКИ.
Схема для наблюдения свободных колебаний в контуре представлена на
рис. 3, установка – на рис. 4.
CR
L
К
12
На вход Y
осциллографа
E
Рис. 3. Схема для изучения
затухающих колебаний.
Возбуждение колебаний в контуре происходит следующим образом. В
положении 1 ключа К конденсатор заряжается до напряжения источника. За-
тем ключ переводят в положение 2, замыкая цепь колебательного контура.
Конденсатор будет разряжаться, и в цепи могут возникать свободные затухаю-
щие колебания.
Рис. 4. Рабочая схема уста-
новки для наблюдения зату-
хающих колебаний.
Переключатель в рабочей схеме можно взять обычный, управляемый вы-
бранной клавишей, но в данном случае более удобным оказывается переключа-
тель, срабатывающий через определенный промежуток времени, устанавливае-
мый пользователем. Наблюдать колебания будем с помощью осциллографа, на
один из каналов которого (например, на вход канала
А) подается исследуемое
напряжение с резистора R. Таким образом исследуются колебания напряжения
на активном сопротивлении. Аналогично можно изучать колебания напряжения
и на других элементах схемы.
Начальные параметры установки выбрать следующими:
Емкость - 10 мкФ;
Индуктивность - 0,1 Гн;
Сопротивление - 20 Ом;
Время срабатывания переключателя после включения питания (опция "Time on"
на вкладке
Value) – 1 мс;
Напряжение источника - 10 В.
Замечание: Все вычисления и построение графиков ведется в электронных таблицах MS
Excel
.

Изучение свободных электрических колебаний в колебательном контуре.
87
Порядок выполнения работы.
Задание № 1. Наблюдение осциллограммы затухающих колебаний. Опреде-
ление периода и частоты колебаний для выбранных парамет-
ров контура
.
1. Подготовить окно программы Electronics Workbench: в диалоговом окне
меню
Analysis/Analysis Options… на вкладке Instruments установить флажок опции
"Pause after each screen" для удобства наблюдения осциллограммы, а также
увеличить минимальное число анализируемых точек до 200-400 (опция "Mini-
mum number of time points").
2. Собрать цепь по рис. 4. Установить указанные выше параметры контура.
3. Подготовить осциллограф к работе. Подобрать коэффициент отклонения
используемого канала и длительность развертки таким образом, чтобы на экра-
не осциллографа полностью укладывался "цуг" затухающих колебаний.
4. Изменяя параметры контура, проследить за влиянием на колебательный
процесс (в частности, на амплитуду, число и период колебаний) каждого из
трех параметров. Результаты наблюдений оформить в виде выводов, сопровож-
дая их математическими выкладками.
5. Подобрать параметры контура таким образом, чтобы число колебаний в
"цуге" было не менее 12-15. Сохранить осциллограмму в виде графика в файле
типа *.gra.
6. Для установленных параметров R, L и C рассчитать собственную цикли-
ческую частоту колебательного контура, коэффициент затухания, циклическую
частоту и период затухающих колебаний. Все вычисления оформить в виде
таблицы в программе MS Excel.
Задание № 2.
Построение графика изменения амплитуды затухающих ко-
лебаний с течением времени.
1. Задание выполняется при полностью развернутом окне осциллографа
(кнопка
Expand). Пользуясь одним из визиров, определить амплитуды колебаний
(
А=
Ro
U ) и соответствующие им моменты времени (t) для полученного цуга из
12-15 колебаний. Занести все данные в таблицу (составляется в MS Excel).
Изучение свободных электрических колебаний в колебательном контуре.
88
№
п/п
t, c
A
, В
T = t
i+1
-t
i
, с
2. Рассчитать период колебаний T, как разность двух соседних значений
времени, а также среднее значение периода и циклическую частоту затухающих
колебаний. Сравнить полученные значения с вычисленными в Задании № 1.
Период колебаний можно также определить непосредственно в програм-
ме Electronics Workbench при помощи осциллографа, используя оба визира
(третье табло под экраном покажет разность моментов времени, соответствую-
щих установленным положениям визиров). При этом визиры можно устанавли-
вать так, чтобы их разделяло несколько периодов, а средний период найдется
как отношение разности соответствующих моментов времени к числу колеба-
ний между ними.
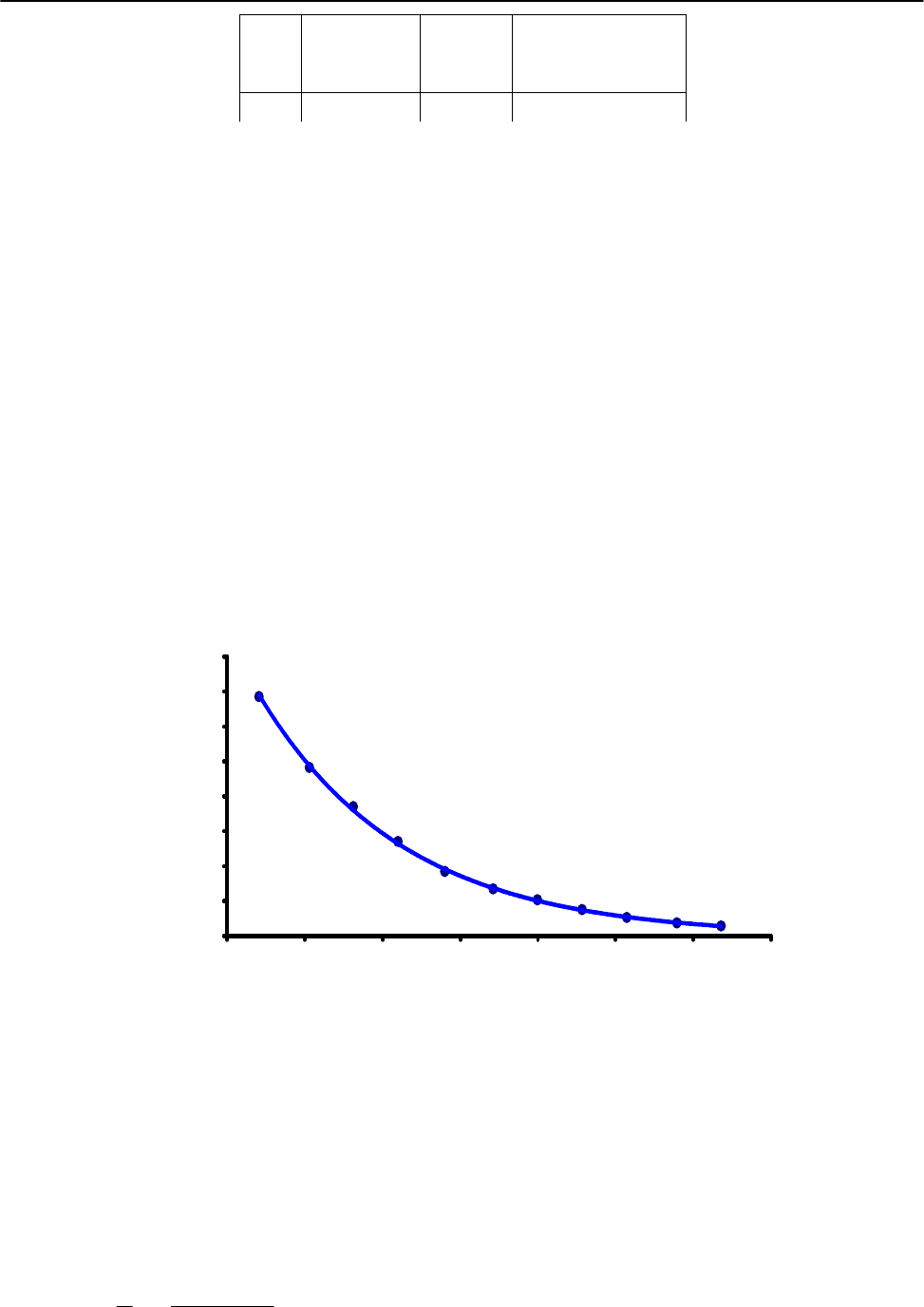
3. По полученным данным построить график зависимости амплитуды от
времени (Точечная диаграмма с маркерами, но без соединяющих отрезков!).
4. Добавить линию тренда (экспоненциальная). Убедиться в том, что экс-
периментальные точки в пределах погрешности измерения укладываются на
данную кривую (см. пример графика на рис. 5).
Изменение амплитуды затухающих колебаний со временем
y = 4,3047e
-0,0107x
0,0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
4,0
0 50 100 150 200 250 300 350
Время, мс
Амплитуда напряжения , В
Рис. 5. Пример графика зависимости амплитуды затухающих колебаний от вре-
мени и экспоненциальная линия тренда с выведенным уравнением кривой.
Задание № 3. Определение логарифмического декремента затухания и
критического сопротивления контура.
1. Используя данные задания № 2 (амплитуды затухающих колебаний) и
определение логарифмического декремента затухания (5), рассчитать λ
эксп
для
каждой пары амплитуд и его среднее значение для всех измерений.
Логарифмический декремент затухания можно также определить для ам-
плитуд, разделенных произвольным числом колебаний n:
)(A
)(A
ln
1
nTt
t
n +
⋅=λ
.

Изучение свободных электрических колебаний в колебательном контуре.
89
2. Сравнить его с вычисленным по формуле T
теор
⋅
β
=
λ
.
3. Используя визиры, по осциллограмме колебаний найти две амплитуды,
отличающиеся примерно в 3 раза (точнее, в е раз), и подсчитать число полных
колебаний между ними - N
e
. Определить логарифмический декремент зату-
хания
λ
граф
по графику, используя его связь с числом N
e
. Сравнить со значе-
ниями, вычисленными в п.п. 1 и 2 задания.
4. Увеличивать величину активного сопротивления контура до исчезнове-
ния колебаний. Выписать соответствующее значение сопротивления – это и бу-
дет критическое сопротивление.
5. Для выбранных параметров L и C контура рассчитать величину критиче-
ского сопротивления по формуле (6). Сравнить ее с экспериментально подоб-
ранным значением. Все результаты оформить в виде таблицы (см. пример ни-
же).
Отчет.
Отчет по работе должен содержать:
1. Схему установки, выполненную в программе схемотехнического моделирования
Electronics Workbench, с экспериментально подобранными параметрами контура.
2. Таблицы с экспериментальными и теоретически рассчитанными величинами (см.
Задания №№ 1-3), а также график зависимости амплитуды затухающих колебаний от време-
ни, выполненные в электронных таблицах MS Excel.
3. Основные выводы по работе.
4. По предложенной (см. приложение к работе
) осциллограмме затухающих колеба-
ний определить неизвестные параметры контура (R, L и С). Проверить правильность расче-
тов с помощью созданной в задании № 1 схеме и при необходимости уточнить их экспери-
ментально. Все вычисления также оформить в MS Excel и приложить к отчету по работе.
Примечание: Все данные сохранять в одной папке - Колебания, которая создается до нача-
ла работы.
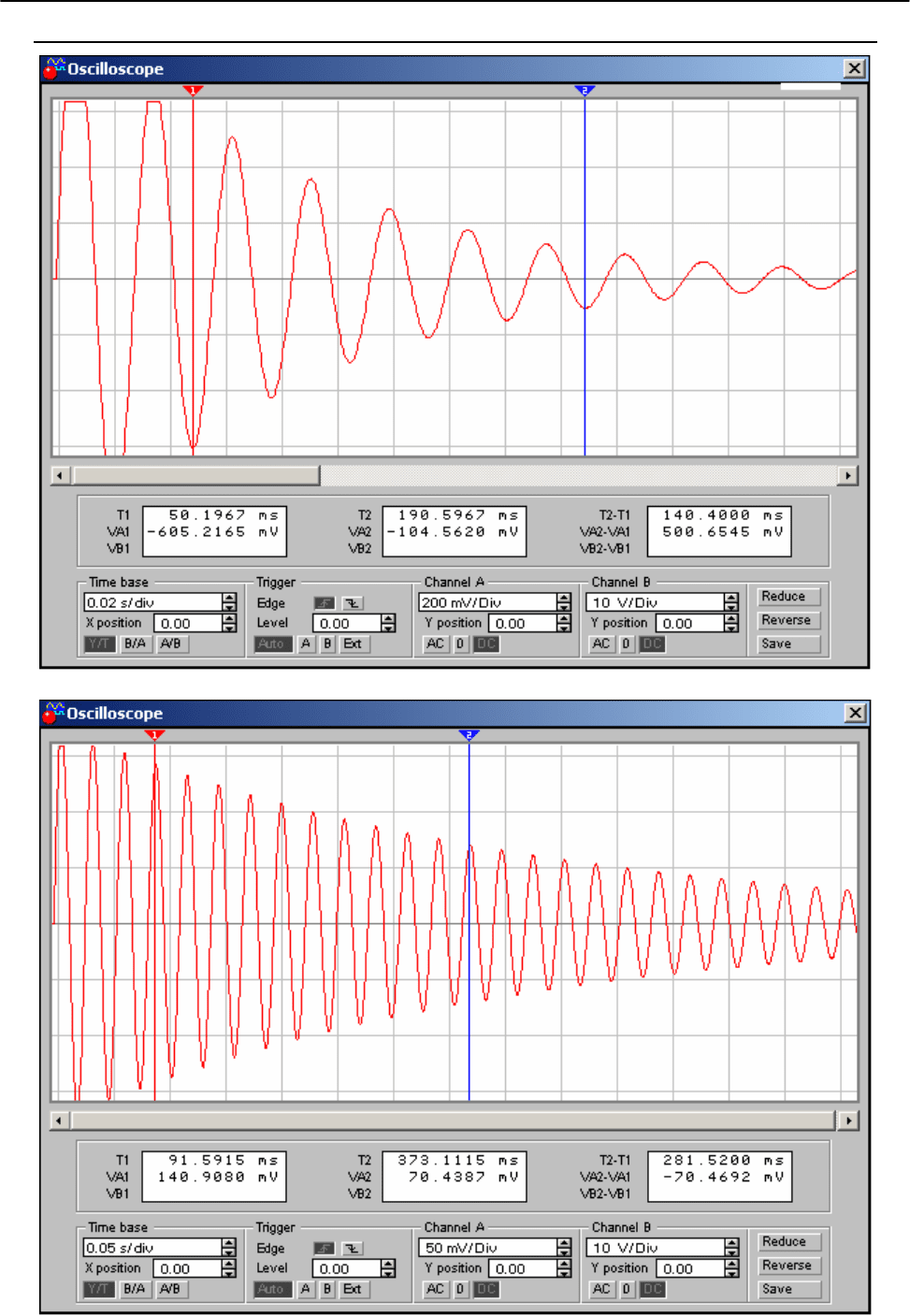
Изучение свободных электрических колебаний в колебательном контуре.
90
Приложение к Лабораторной работе по изучению затухающих колебаний.
R=50 Ом
L=2 Гн
