Щеглова И.Ю., Печенов В.В. Виртуальный физический практикум
Подождите немного. Документ загружается.


Изучение электронного осциллографа.
51
ние. Получить осциллограмму и объяснить ее вид.
11. Для синусоидального сигнала отключить генератор развертки сначала
кнопкой
A/B, а затем – В/А. Что представляет собой осциллограмма в каждом из
этих случаев? Объяснить результат.
12. Включить генератор развертки и перевести его в ждущий режим
по
используемому входу. Установить уровень синхронизации
, отличный от нулево-
го. Включить питание, проследить за изменениями осциллограммы. Получить
несколько осциллограмм для различных значений уровня синхронизации. Со-
хранить одну из осциллограмм в виде графика.
13. Изменяя смещение сигнала по постоянному току (переключатель
Offset
функционального генератора), проследить за смещением осциллограммы по
вертикали в зависимости от выбранной связи с источником сигнала (открытый
или закрытый вход).
14. Подать на вход осциллографа сигнал определенной величины и часто-
ты с источника переменного напряжения. Определить амплитудное значение
исследуемого напряжения с помощью осциллографа и найти его связь с уста-
новленным на выходе источника. Как называется напряжение, указанное на ис-
точнике?
Задание № 2.
Использование осциллографа в качестве частотомера.
Подадим на обе пары отклоняющих пластин переменные напряжения
x
U
и
y
U
, меняющиеся по синусоидальному закону (для простоты предположим,
что эти напряжения имеют равные частоты).
ϕ+ω⋅=
ω⋅=
).sin(
,sin
max
max
tUU
tUU
yy
xx
Под воздействием этих напряжений, в зависим ости от соотношения их
частот, амплитуд и фаз, можно получить различные осциллограммы. При этом
луч будет совершать колебания в двух взаимно перпендикулярных направлени-
ях:
ϕ+ω⋅=
ω⋅=
);sin(
,sin
tBy
tAx
где А и В – амплитудные, а x и y - мгновенные значения отклонения пятна в го-
ризонтальном и вертикальном направлениях. Исключим из приведенных урав-
нений время:
()
ϕ⋅−+ϕ⋅=
ϕ⋅−⋅+ϕ⋅ω⋅=
=ω
).sincos(
,sin1cossin
,sin
22
2
xAx
A
B
y
A
x
BtBy
A
x
t
В общем случае это выражение представляет собой уравнение эллипса, в
Изучение электронного осциллографа.
52
частном – прямой или окружности.
Действительно, в случае равенства частот и отличных амплитуд и фаз
сложение этих колебаний дает на экране эллипс.
При равенстве амплитуд, частот и фаз уравнение примет вид:
x
y = и на
экране ЭЛТ получится прямая линия.
Окружность получается в случае сложения двух колебаний с равными
частотами, амплитудами и отличающимися по фазе на
2
/
π
=
ϕ
. При других со-
отношениях частот, амплитуд и фаз осциллограммы могут иметь вид более
сложных кривых – фигур Лиссажу.
Фигура Лиссажу - замкнутая кривая, полу-
чаемая на экране осциллографа при сложении взаимно перпендикулярных ко-
лебаний, подаваемых на отклоняющие пластины, если частоты этих колебаний
равны или кратны. По этим фигурам определяют частотные, фазовые или ам-
плитудные соотношения напряжений, подаваемых на отклоняющие пластины.
1. Выбрать синусоидальную форму выходного сигнала генератора. Подать
на второй вход осциллографа сигнал с выхода источника переменного напря-
жения и отключить генератор развертки. Установить одинаковую частоту пода-
ваемых сигналов (соотношение частот в этом случае будет 1:1).
2. Включить питание и подобрать коэффициент отклонения по каждому из
каналов так, чтобы фигура полностью уложилась в размеры экрана.
3. Изменяя начальную фазу сигнала источника переменного напряжения,
получить несколько фигур Лиссажу. Зарисовать (или сохранить в виде графика)
те из них, которые соответствуют разности фаз: 0,
4
π
, 2
π
, 43π и π.
4. Получить фигуры для различных соотношений частот (1:2; 2:1; 2:3; 4:3;
5:2; 3:5 и некоторых других) и сдвига фаз.
Примечание: каждый раз после получения фигуры Лиссажу необходимо отключать
питание схемы
.
Задание № 3. Сложение гармонических колебаний одного направления. Бие-
ния.
При сложении двух колебаний с близкими частотами возникают биения,
частота которых равна разности данных частот. Результирующее колебание
можно рассматривать как гармоническое колебание с пульсирующей амплиту-
дой (см. рис. 7).
Рассмотрим сложение колебаний, описываемых уравнениями:
()
ϕ
+
ω⋅=ω⋅= tBytAy
121
cos;cos ,
где
A и B – амплитуды колебаний, ϕ - разность (сдвиг) фаз. Возьмем наиболее
простой случай, когда
А=В и ϕ=0:
(
)
tAtAytAy
ω
∆
+
ω
⋅
=
ω⋅=ω⋅= coscos;cos
121
.
Поскольку частоты колебаний близки,
ω
<
<
ω
∆
. При сложении этих колебаний
возникает сложное колебательное движение
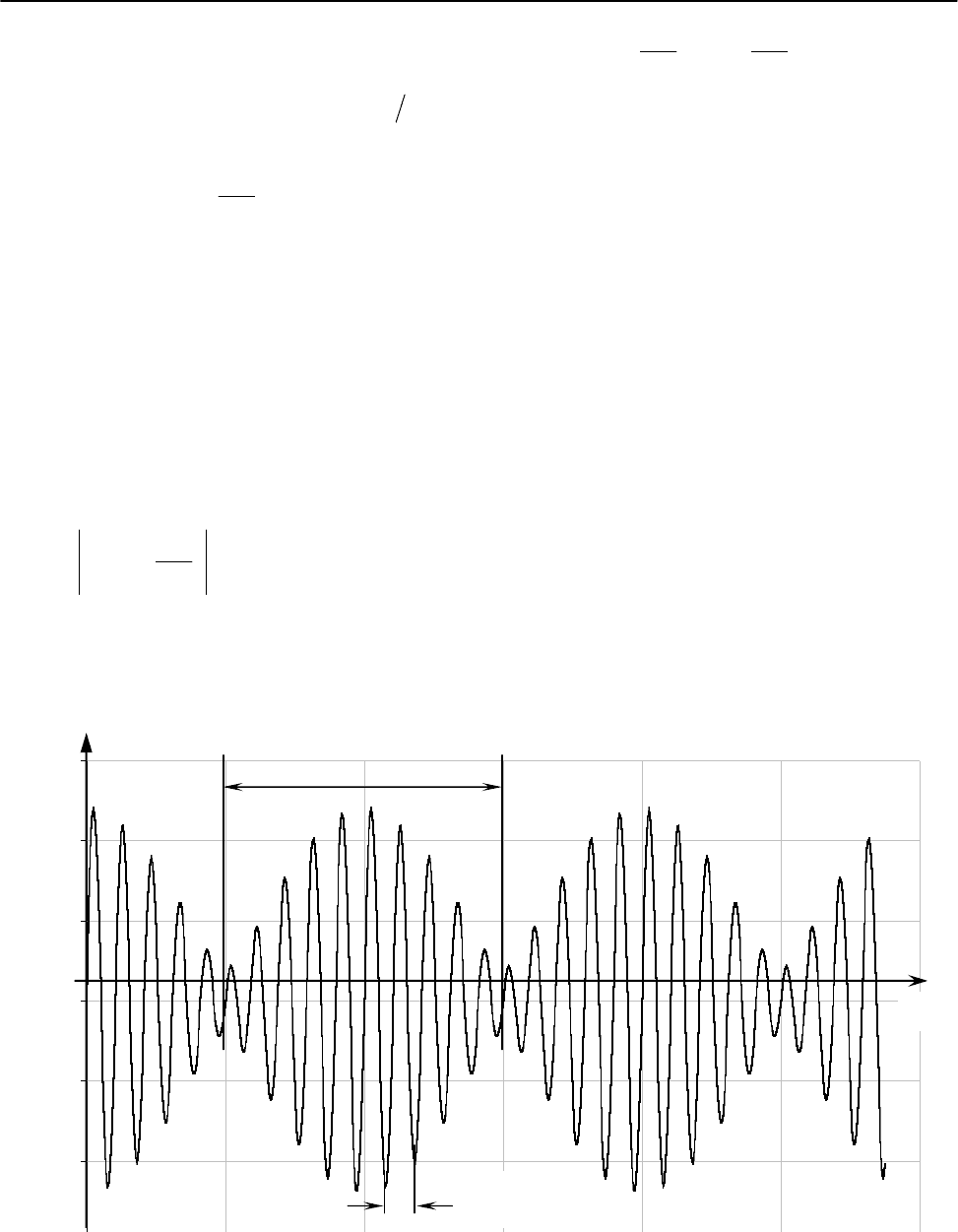
Изучение электронного осциллографа.
53
()()
ttAttAyyy
2
cos
2
cos2coscos
21
ω∆
⋅
ω∆
+ω=ω∆+ω+ω=+=
.
В первом множителе членом
2
ω
∆ по сравнению с ω можно пренебречь. В ре-
зультате получаем:
ttAy ω
ω∆
⋅= cos
2
cos2
. (1)
Заключенный в скобки множитель в последней формуле изменяется гораздо
медленнее, чем второй множитель. Ввиду условия
ω
<
<
ω
∆
за то время, за ко-
торое множитель
t
ωcos совершает несколько полных колебаний, множитель,
стоящий в скобках почти не изменится. Это дает основание рассматривать ко-
лебание (1) как гармоническое колебание частоты ω, амплитуда которого изме-
няется по некоторому периодическому закону. Выражением этого закона не
может быть множитель, стоящий в скобках, т.к. он изменяется в пределах от
-2
А до +2А, в то время как амплитуда по определению – положительная вели-
чина. Аналитическое выражение амплитуды, очевидно, имеет вид:
tA
2
cos2
ω∆
. (2)
Функция (2) – периодическая функция с частотой, в 2 раза превышающей час-
тоту выражения, стоящего под знаком модуля (или, что то же самое, стоящего в
скобках в (1)), т.е. с частотой ∆ω. Таким образом, частота пульсаций – ее назы-
вают частотой биений – равна разности частот складываемых колебаний.
Рис.7. Результат сложения гармонических колебаний одного направления (бие-
ния).
T
б
– период биений; Т – период колебаний.
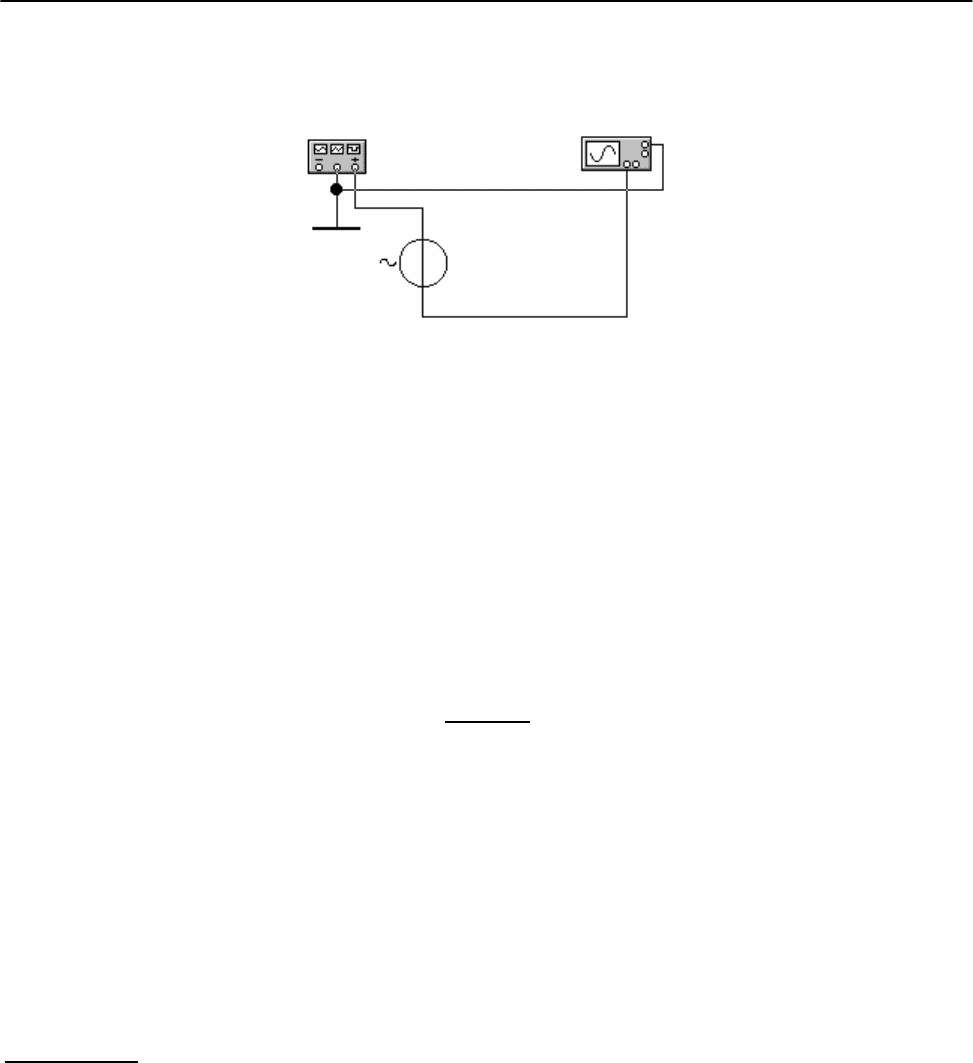
1. Собрать схему по рис. 8. В качестве источников синусоидальных коле-
баний здесь используются функциональный генератор и источник переменного
напряжения. Установить одинаковые амплитуды и частоты колебаний.
T
б
=2π/∆
ω
Т=2
π
/
ω
t
y
Изучение электронного осциллографа.
54
2. Включить питание схемы и подобрать коэффициент отклонения таким
образом, чтобы размах колебаний не превышал размера экрана осциллографа
по вертикали (т.е. был не более 6 делений масштабной сетки).
Рис. 8. Схема установки для наблюдения биений.
3. Уменьшая частоту генератора и подбирая длительность развертки, полу-
чить на экране осциллографа 3-4 периода биений. Выписать частоты колебаний
и их разность. Сохранить результаты в виде графика.
5. Пользуясь визирами, определить период биений и период колебаний, и
рассчитать частоты биений и колебаний. Сравнить с выписанными значениями.
6. Получить биения для 2-3 значений частот.
7. Получить осциллограмму для случая, когда частоты складываемых ко-
лебаний отличаются в 10 и 100 раз. Сохранить результаты в виде графика.
Отчет.
Отчет по работе должен содержать:
1. Схему установки для наблюдения кривой напряжения, выполненную в программе
схемотехники Electronics Workbench.
2. Осциллограммы исследуемых сигналов различной частоты (сохраненные в виде
графиков); их амплитуда, период и частота (расчет).
3. Фигуры Лиссажу для различных соотношений частот и фаз и схема для их наблю-
дения.
4. Схему для наблюдения биений, осциллограммы биений (в виде графиков) и расчет
их частоты.
5. Основные выводы по работе.
Примечание: Все данные сохранять в одной папке - Осциллограф, которая создается до
начала работы.
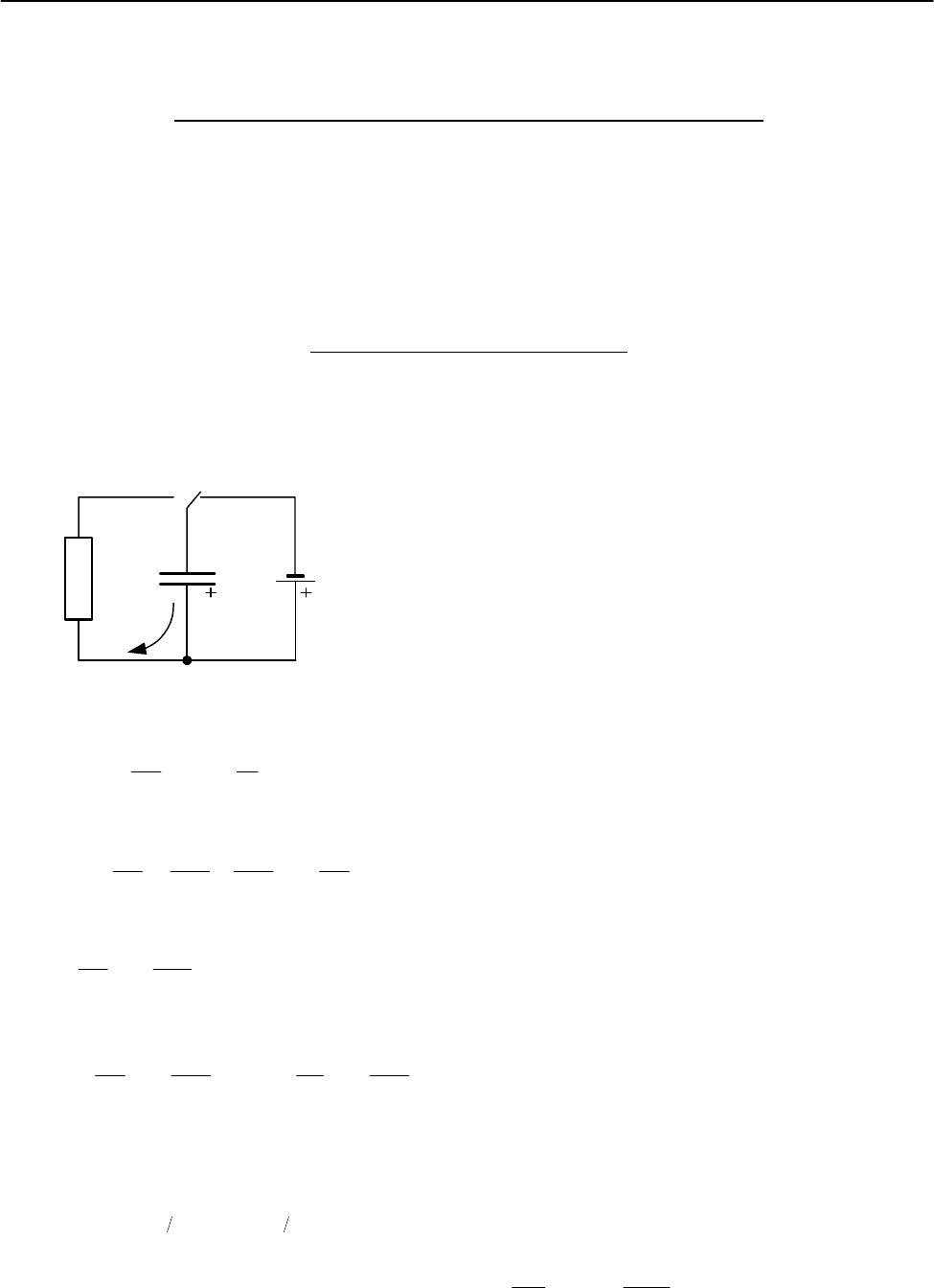
Дифференцирующие и интегрирующие цепи.
55
Лабораторная работа № 2.3.
ДИФФЕРЕНЦИРУЮЩИЕ И ИНТЕГРИРУЮЩИЕ RC- И RL-ЦЕПИ.
1. Изучение процесса протекания тока в RC-цепи.
Рассмотрим процессы, происходящие в цепи с конденсатором (процессы
зарядки и разрядки конденсатора), и при этом будем полагать, что
1) мгновенное значение тока одно и тоже во всех сечениях проводника,
соединяющего обкладки конденсатора;
2) мгновенное электрическое поле такое же, как в электростатике при тех
же значениях заряда на обкладках конденсатора.
1.1. Разрядка конденсатора.
Рассмотрим цепь, состоящую из источника тока, конденсатора и резисто-
ра. С помощью переключателя конденсатор можно подключать к источнику
постоянного напряжения.
E
R
C
12
Если затем замкнуть обкладки заря-
женного конденсатора проводником, имею-
щим сопротивление
R, в цепи появится элек-
трический ток. Обозначим через
i, q и
C
u
мгновенные значения тока, заряда положи-
тельной обкладки и разности потенциалов
между обкладками. Будем считать ток поло-
жительным, когда он течет от положительной
обкладки к отрицательной. Тогда
t
q
i
d
d
−=
,
C
q
u
C
=
,
iRuu
CR
==
.
Отсюда
t
q
RC
q
RC
q
R
u
i
R
d
d
; −===
.
После разделения переменных
t
RCq
q
d
1d
−=
и интегрирования получим:
RC
t
q
q
t
RCq
q
o
t
q
q
o
−=−=
∫∫
ln,d
1d
0
,
где
q
o
– начальное значение заряда конденсатора (в момент времени t
o
=0).
Обозначим произведение
RC через τ. Потенцируя последнее выражение,
получим:
τ−−
==
t
o
RCt
o
eqeqq
)(
.
Найдем размерность τ :
[]
с
В
сА
Ом
В
Кл
ОмФОмRC =
⋅
⋅=⋅=⋅=
.
Таким образом, данная величина имеет размерность времени и называется
вре-
менем релаксации
или постоянной времени. Физический смысл ее состоит в
Дифференцирующие и интегрирующие цепи.
56
том, что через время τ заряд конденсатора убывает в e раз:
e
q
qeqqt
o
o
=⇒=τ=
−1
;
.
Закон изменения тока найдем, как производную заряда по времени:
τ−
τ
=−=
t
o
e
q
t
q
i
d
d
,
где
τ
=
o
q
I
0
- начальное значение тока, т.е. ток в момент времени
0=
o
t
.
Разность потенциалов на обкладках конденсатора также изменяется по
экспоненциальному закону.
τ−τ−
===
t
C
t
o
C
eUe
C
q
C
q
u
o
,
где
o
C
U - начальное значение разности потенциалов на обкладках конденсатора.
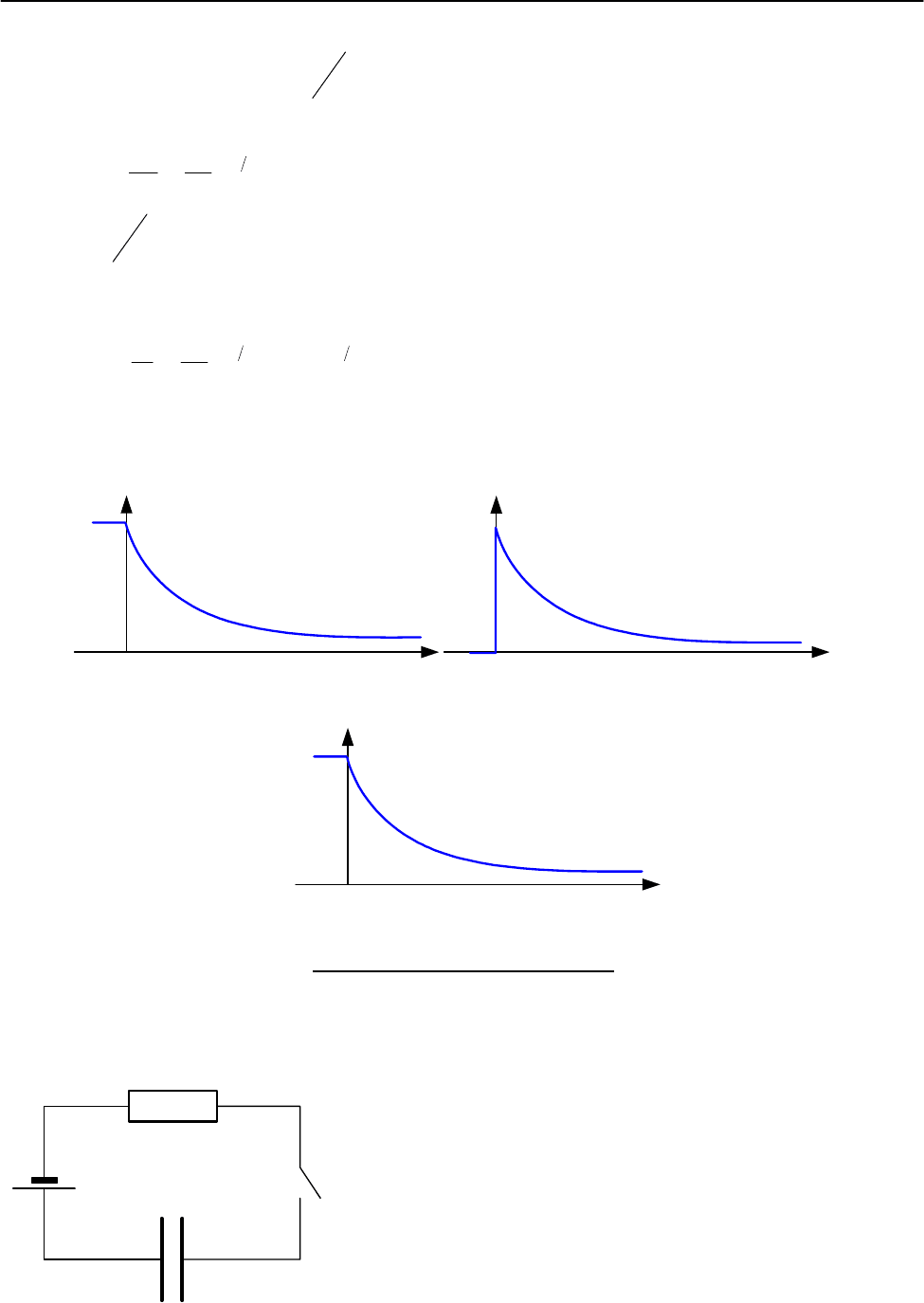
Представим эти процессы графически.
q
t
t
u
C
i
U
Co
I
o
q
o
t
1.2. Зарядка конденсатора.
Пусть незаряженный конденсатор подключается к источнику тока с по-
стоянной электродвижущей силой Е.
R
C
E
-
+
Обозначим сопротивление резистора,
включенного последовательно с конденсато-
ром, через
R. При замыкании такой цепи в ней
потечет электрический ток, заряжающий кон-
денсатор. Электрические заряды, возникающие
на обкладках конденсатора, препятствуют про-
хождению тока и уменьшают его. Будем теперь
считать положительным ток, текущий к поло-
жительной обкладке. Тогда
Дифференцирующие и интегрирующие цепи.
57
R
u
i
C
q
u
t
q
i
C
C
−
===
E
,,
d
d
.
Исключая снова
i и u
C
, получим
RRC
q
t
q
C
q
R
t
q E
d
d
,E
d
d
=+−=
.
Это неоднородное уравнение можно свести к однородному, если записать его в
виде:
()
0
E
E
d
d
=
−
+−
RC
Cq
Cq
t
.
Решим его:
() ()
∫∫
−=
−
−
−=
−
−
;d
1
E
Ed
;
d
E
Ed
t
RCCq
Cq
RC
t
Cq
Cq
()
A
RC
t
Cq lnEln +−=−
,
где ln
A – постоянная интегрирования. Отсюда после потенцирования
.E
;E
τ−
τ−
⋅+=
⋅=−
t
t
eACq
eACq
Значение постоянной
А найдем из начальных условий: в момент времени t
o
=0
конденсатор не был заряжен, т.е.
0
=
o
q
. Отсюда
C
A
E
−
=
.
(
)
τ−τ−
−⋅=⋅⋅−⋅=
tt
eCqeCCq 1E;EE.
При
∞→
t
заряд q стремится к предельному значению
Cq E
=
∞
.
Для тока:
τ−τ−
=
τ
==
tt
e
R
e
C
t
q
i
EE
d
d
.
В начальный момент времени ток максимален и равен
R
I
o
E
= . В дальнейшем
он убывает по экспоненциальному закону.
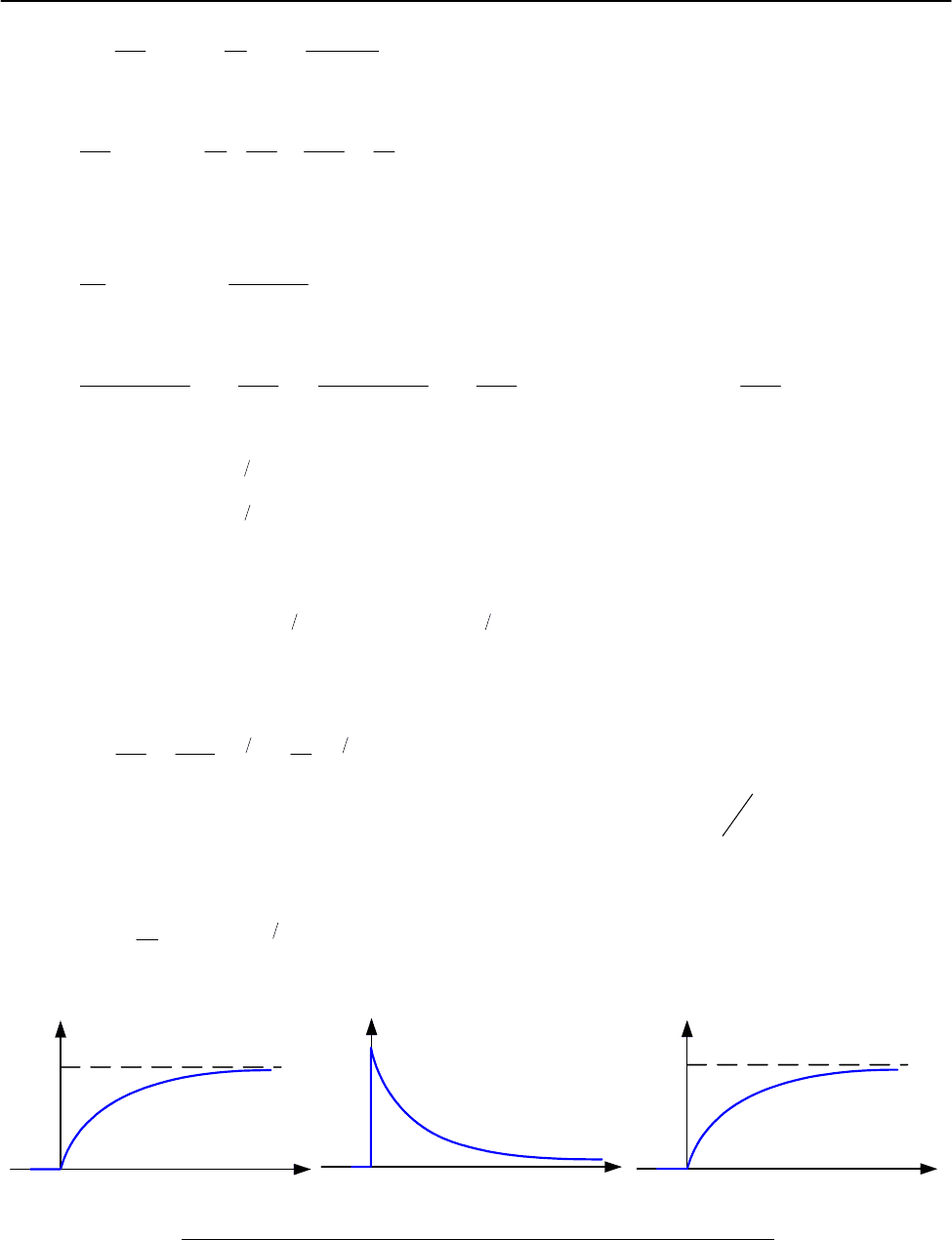
Для разности потенциалов:
()
τ−
−==
t
C
e
C
q
u 1E
.
Графики процессов:
1.3. Дифференцирующая и интегрирующая RC-цепь.
Пусть теперь на вход RC-цепи подается переменное напряжение
)(tu
вх
.
Найдем связь между падениями напряжения на емкости и активном сопротив-
лении и входным напряжением. Распишем напряжение на входе схемы
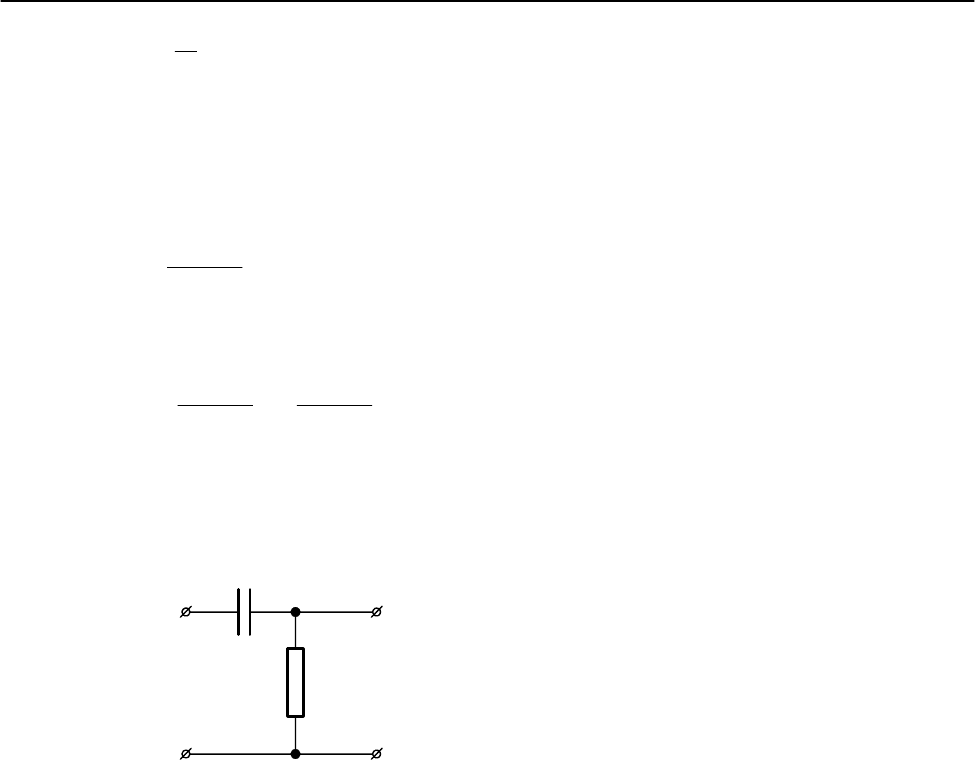
Дифференцирующие и интегрирующие цепи.
58
.)(d)()(
;)(d)(
1
)(
∫
∫
⋅=⋅+⋅τ
=⋅+⋅
tuCttiti
tutti
C
tiR
вх
вх
Рассмотрим два предельных случая:
1) Если τ очень мало, то первым слагаемым в последнем уравнении мож-
но пренебречь. Тогда, дифференцируя оставшееся уравнение по
t, получим:
t
tu
Cti
вх
d
)(d
)( ≈
.
Напряжение на резисторе, равное
)(tiRu
R
⋅
=
совпадает по форме с током и,
следовательно, пропорционально производной входного сигнала
.
d
)(d
d
)(d
t
tu
t
tu
RCu
вхвх
R
τ=≈
Таким образом, напряжение на резисторе с точностью до числового множителя
равно производной от входного напряжения, и мы приходим к схеме
диффе-
ренцирующей цепи
, в которой выходной сигнал снимается с резистора
(рис. 1).
C
R
u
вх
u
вых
Рис. 1. Дифференцирующая RC-цепь.
Наиболее интересным и важным для практики является случай прохож-
дения прямоугольных импульсов через дифференцирующую
RC-цепь. В этом
случае условие "малости τ" означает, что постоянная времени должна быть
много меньше длительности импульса (τ=
RC<<t
и
). Эту цепь применяют в тех
случаях, когда импульсы сравнительно большой длительности необходимо
преобразовать в короткие запускающие импульсы с крутым фронтом. Если при
подаче входного импульса конденсатор не был заряжен, то в первый момент
через конденсатор, а также через резистор будет протекать большой ток. Таким
образом, на резисторе сразу же появляется большое падение напряжения
(рис. 1.1), благодаря чему на выходе очень быстро нарастает фронт импульса.
По мере увеличения заряда конденсатора протекающий через него ток умень-
шается со скоростью, зависящей от постоянной времени цепи. Когда конденса-
тор полностью заряжается, ток перестает протекать по цепи, и напряжение на
резисторе
R спадает до нулевого уровня. В момент окончания действия им-
пульса входное напряжение уменьшается до нуля, и конденсатор начинает раз-
ряжаться. Ток разрядки конденсатора имеет противоположное по сравнению с
током зарядки направление, следовательно, направление тока через резистор
также противоположно току зарядки. Поэтому на выходе теперь появится от-
рицательный всплеск напряжения.
Дифференцирующие и интегрирующие цепи.
59
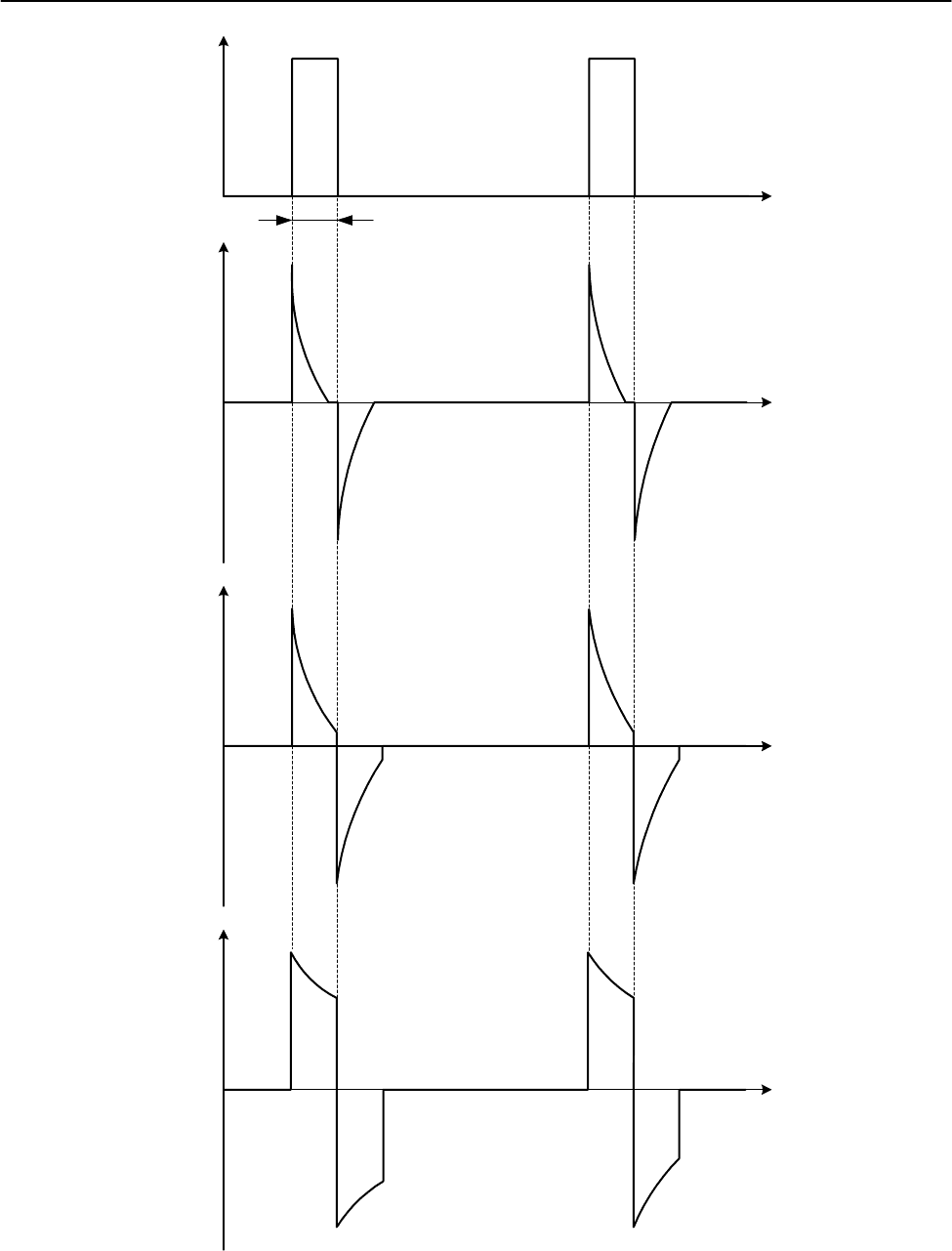
u
вх
t
t
t
t
u
вых
u
вых
u
вых
t
и
Рис. 1.1. Изменение формы импульсов на выходе дифференцирующей RC-цепи
при увеличении постоянной времени.
Если на вход дифференцирующей цепи подать синусоидальный сигнал,
то форма его не изменится, но произойдет сдвиг фазы выходного колебания и
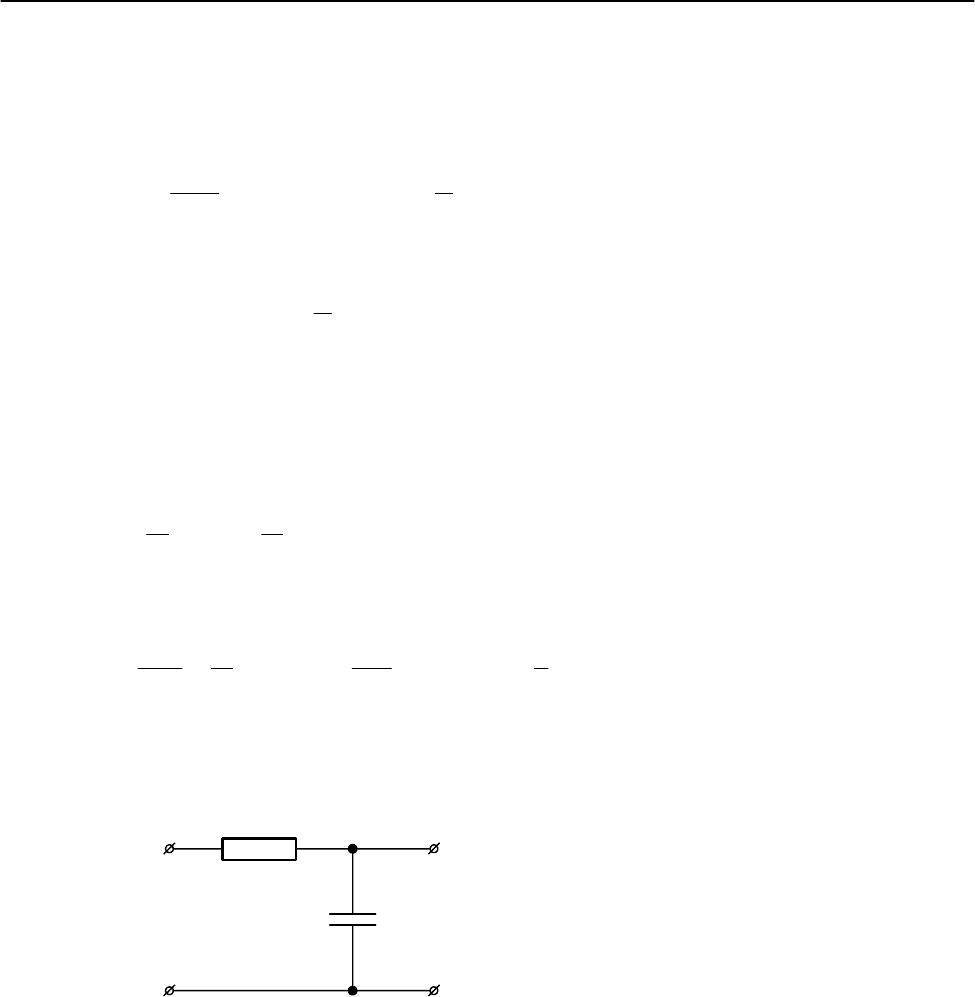
Дифференцирующие и интегрирующие цепи.
60
уменьшение амплитуды этих колебаний на величины, зависящие от частоты
входного сигнала. Пусть
tUu
вхвх
ω= sin
o
.
При точном дифференцировании
π
+ωω==
2
sin
d
d
o
tUa
t
u
au
вх
вх
вых
.
Обозначив
оо
выхвх
UUa =ω , получим
π
+ω=
2
sin
o
tUu
выхвых
.
Таким образом, выходное напряжение оказывается сдвинутым относительно
входного на π/2.
2) Если τ очень велико, то можно отбросить второе слагаемое, в этом слу-
чае ток
)(
1
)()( tu
R
tu
C
ti
вхвх
=≈
τ
совпадает по форме с входным сигналом, а напряжение на конденсаторе
C,
равное
∫∫∫
⋅
τ
=⋅≈⋅== ttuttu
R
C
tti
CC
tq
u
вхвхC
d)(
1
d)(
1
d)(
1)(
,
пропорционально интегралу от входного сигнала. Таким образом, мы приходим
к
интегрирующей цепи (рис. 2), в которой выходное напряжение снимается с
конденсатора
.
C
R
u
вх
u
вых
Рис. 2. Интегрирующая RC-цепь.
Рассмотрим, что происходит в такой цепи при подаче на нее последова-
тельности прямоугольных импульсов. Для интегрирующей
RC-цепи постоянная
времени должна быть много больше длительности воздействующего импульса
(τ=
RC>>t
и
). При подаче на вход схемы положительного импульса крутой фронт
импульса действует на интегратор в течение очень короткого времени. Затем в
течение времени, равного длительности импульса, действует напряжение, соот-
ветствующее плоской вершине импульса. Напряжение на конденсаторе нарас-
тает по экспоненциальному закону. Так как
и
t>>
τ
, напряжение на конденсато-
ре не достигает максимального значения, а нарастает до определенной величи-
ны.
По окончании действия входного импульса конденсатор начнет разря-
жаться через резистор
R и входную цепь. Разряд протекает также медленно по
сравнению со спадом входного импульса, в результате чего на выходе форми-
