Сборник трудов конференции Павловские чтения 2010
Подождите немного. Документ загружается.

Секция 4. Сортопрокатное и волочильное производство
420
P
(i)пр
(v
i
)=f
i
(P
(i)
'(v
i
) ), (1)
где P
(i)
'(v
i
) - точки сегмента ручья; P
(i)пр
(v
i
) - точки соответствующего сегмента на проводке; f
i
- закон отображения каждой пары соответствующих точек; i = 1,2,3,4,5; v– параметр сегментов
Безье, v
∈
[0,1], у выбранных для проектирования пятерок точек.
Выбор каждой из пяти точек на заданном сегменте ручья калибра может быть осуществлен
произвольно. Но для построения характеристической ломаной по спроектированным точкам с
целью задания искомой кривой в форме Безье и отыскания значений полноты w
1
в основных ха-
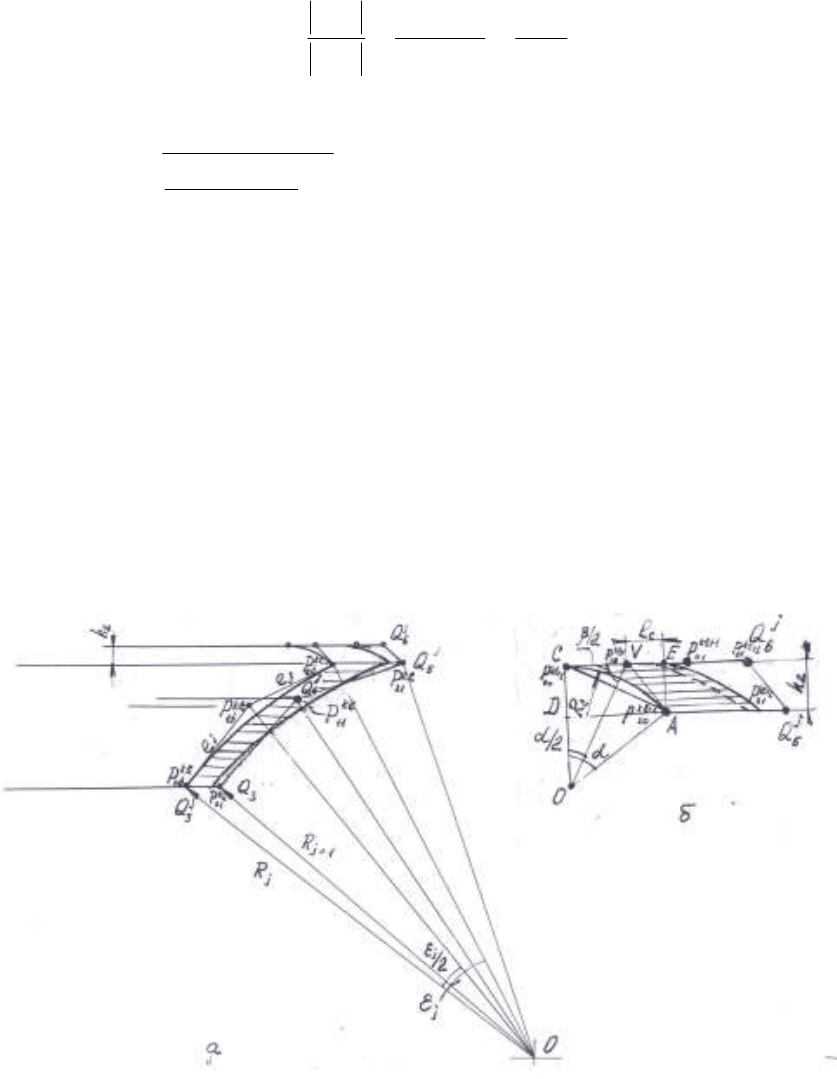
рактеристических точках удобно выбрать следующие точки (см.рис. 2,б):
- концы сегмента, совпадающие с вершинами P
0
' и P
2
'его характеристической ломаной, кото-
рым соответствуют значения параметра v = 0 и v = 1 (P
(1)
'(0), P
(5)
'(1));
-
точку максимума квадратичного сегмента с параметром v = 0,5 , которая согласно [2] лежит
на медиане треугольника, образованной характеристической ломаной, и проведенная в этой точ-
ке касательная к кривой будет параллельна основанию треугольника (P
(3)
'(0.5)).
Положение оставшейся пары точек получим следующим образом:
- разобъем рассматриваемый сегмент (см. рис.2,б) на две части P'
(I)
(v') и P'
(II)
(v') , соеди-
няющиеся в точке O, тождественной P
3
'(0.5), и задаваемых своими характеристическими лома-
ными P
0
'
(I)
, P
1
'
(I)
, P
2
'
(I)
и P
0
'
(II)
, P
1
'
(II)
, P
2
'
(II)
, причем смежные их стороны и P
1
'
(I)
P
2
'
(I)
и P
0
'
(II)
P
1
'
(II)
лежат на касательной к точке максимума старого сегмента P
(3)
'(0.5); а w
1
'
(I)
= w
1
'
(II)
=w
1
;
- по аналогии с большим сегментом возьмем точки максимумов у новых сегментов, которым
будет соответствовать значение нового параметра v'=0.5(P'
(I)
(0.5), P'
(II)
(0.5)).
Представим эти точки как функции от первоначального параметра v. Согласно [2] такое пре-
образование обеспечивается формулой
v=(1- v')v
0
+ v'v
1
,
где - v' , v
1
- первоначальные параметры конечных точек модифицируемого сегмента.
Подстановка в формулу значений параметров для точки P'
(I)
(0.5) дает
v=0.5·0 + 0.5·0.5=0.25 ,
а для точки P'
(II)
(0.5)
v=0.5·0.5 + 0.5·1=0.75 .
Таким образом, оставшейся паре точек будут соответствовать значения параметра v = 0,25 и v
= 0,75, а их обозначения P'
(I)
(0.5) и P'
(II)
(0.5) после приведения к первоначальному сегменту будут
P
(2)
'(0.25) и P
(4)
'(0.75) соответственно.
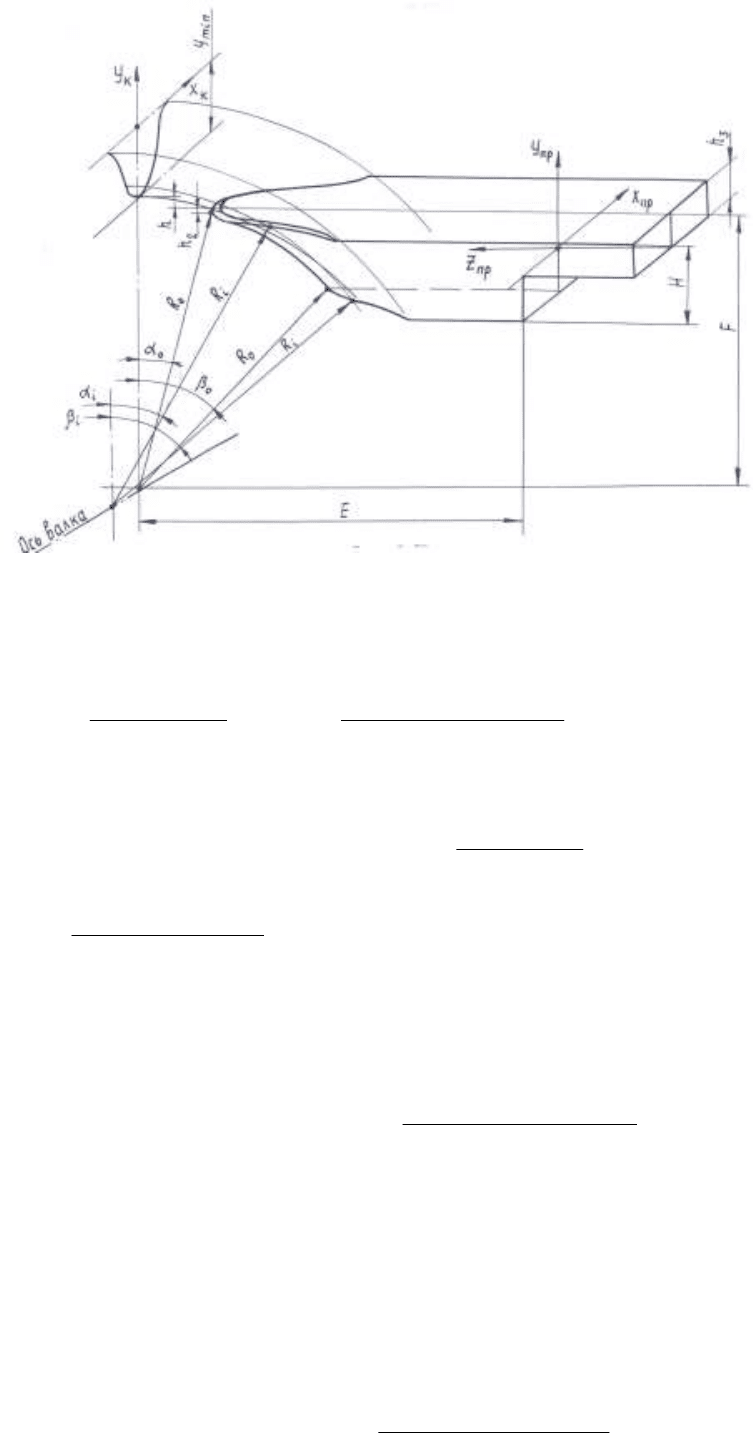
Чтобы определить закон отображения точек f
i
, рассмотрим продольное сечение находящейся в
ручье проводки (рис. 3). Начало системы координат ручья x
0p
*
, y
0p
*
поместим в точке пересечения
вертикальной плоскости, проходящей через линию прокатки, с осью валка (в нашем случае ниж-
него). Эта система координат может свободно вращаться относительно оси валка x
в
*
, а следова-
тельно, ордината y
в
*
будет соответствовать радиусу вращения R
i
.
Положение выбранной точки контура калибра относительно нового начала координат O' мо-
жет быть выражено как
x
i
*
= x
pi
, y
i
*
= R
i
= R
д
+ y
min
– s/2 – y
pi
, (2)
где R
д
- радиус дна ручья; y
min
- самая нижняя точка ручья относительно начала координат ка-
либра; s/2 - половина величины зазора между буртами валков. Величина радиуса ручья R
i
может
изменяться в пределах от R
д
до R
д
+ y
min
– s/2.
Спроектируем каждую из пяти выбранных на рассматриваемом сегменте точек на плоскость
верхней грани участка прилегания носка проводки к валку (см. рис.2, б):
P
i
'(u)→P
i пр
(v) .
Проводка в ручье валка
Секция 4. Сортопрокатное и волочильное производство
421
Рис.3
Как видно из рис.3 положение проекции каждой точки зависит от угла α
i
, величина которого,
в свою очередь, зависит от величины R
i
и может быть выражена как
)
2/
arccos()
)(
arccos(
min
22
piд
д
i
д
i
ysyR
hhR
R
hhR
−−+
−
−
=
−
−
=
α
(3)
Величина угла α
i
меняется в пределах от
)arccos(
2
0
д
д
R
hhR
−
−
=
α
до
)
2/
arccos(
min
2
syR
hhR
д
д
п
−+
−−
=
α
.
Проекция ординаты проектируемой точки R
i
на заданную плоскость находится по формуле
S
1yi
= R
i
sin( α
i
), подстановка в которую соответствующего выражения из (2) и (3) дает
))
2/
(sin(arccos)2/(
min
2
min1
piд
д
piдyi
ysyR
hhR
ysyRS
−−+
−
−
−−+=
. (4)
Абсцисса спроектированной точки равна абсциссе проектируемой, т.е. с учетом (2) равна абс-
циссе в системе координат калибра S
1xi
.=x
i
*
=x
pi
. Завершив проектирование точек сегмента ручья
на заданную плоскость, преобразуем их координаты применительно к системе координат провод-
ки, в которой они примут вид:
x
пр
i
=x
pi
,
y
пр
i
=F ,
z
пр
i
=E-S
1yi
=E-(R
д
+y
min
-s/2-y
pi
)
))
2/
(sin(arccos
min
2
piд
д
ysyR
hhR
−−+
−
−
. (5)

Секция 4. Сортопрокатное и волочильное производство
422
С учетом полученных результатов уравнение (1) после подстановки в него (5) приобретает
вид:
x
прi
(v
i
)=x
pi
(v
i
) ,
y
прi
(v
i
)=F+h
3
-h
2
,
z
прi
(v
i
)= E-S
1yi
=E-(R
д
+y
min
-s/2-y
pi
(v
i
) (
))
)(2/
(sin(arccos
min
2
ipiд
д
vysyR
hhR
−−+
−
−
v
i
{
}
.5,4,3,2,1;1;75.0;5.0;25.0;0 =∈ i
(6)
По аналогии с (3), (4), (6) для нижней грани проводки имеем:
)
2/
arccos()arccos(
min
syR
HhR
R
HhR
д
д
i
д
i
−+
−−
=
−−
=
β
, (7)
где величина угла β
i
меняется в пределах от
)arccos(
д
д
R
HhR
−
−
до
)
2/
arccos(
min
syR
HhR
д
д
−+
−−
.
Проекция ординаты проектируемой точки R
i
на заданную плоскость находится по формуле:
))
2/
(sin(arccos)2/(sin
min
min2
piд
д
piдiiyi
ysyR
HhR
ysyRRS
−−+
−
−
−−+==
β
.
С учетом полученных результатов окончательно имеем:
x
прi
(v
i
)=x
pi
(v
i
) ,
y
прi
(v
i
)=F+h
3
-H
,
))
)(2/
(sin(arccos))(2/()(
min
min
ipiд
д
ipiдiпрi
vysyR
HhR
vysyREvz
−−+
−
−
−−+−=
v
i
{
}
.5,4,3,2,1;1;75.0;5.0;25.0;0 =∈ i
Для построения характеристической ломаной сегмента Безье по его пяти найденным выше
точкам, обозначим спроектированные точки P
(2)пр
(0.25), P
(4)пр
(0.75) как D и L. Точки P
(0)пр
(0),
P
(3)пр
(0.5), P
(5)пр
(1) соединим друг с другом, обозначив вершины получившегося треугольника A,
O
1
, C соответственно см. рис. 2). Середины его сторон AO
1
, O
1
C ,AC обозначим Н, К, Е. Через
точку O
1
проведем прямую (FG), параллельную основанию АС. Соединив точки H и D, а также K
и L, проведем прямые (HD) и (KL), которые пересекутся с построенной прямой в точках F и G.
Достроим треугольники AO
1
F и O
1
GC, проведя через точки F и G прямые (AF) и (BG), которые
пересекутся в точке B. Так как прямые (FH), (GK) и (BE) соединяют вершины соответствующих
треугольников с серединами соответствующих сторон, то они являются медианами.
Рассматривая треугольники A O
1
,C , DO
1
H, FO
1
H, определим длины сторон треугольника че-
рез координаты соответствующих векторов:
=−= OAOCAC
( ) ( )
0
22
lzzxx
acac
=−+−
,
где точка О - начало координат проводки (см.рис.3);
( ) ( )
1
22
22
1
l
zzxx
ACAE
AcAc
=
−+−
−=
;
=−= OAOOAO
11
( ) ( )
2
2
1
2
1
lzzxx
AOAO
=−+−
;

Секция 4. Сортопрокатное и волочильное производство
423
( ) ( )
3
2
1
2
111
22
l
zz
z
xx
xOEOOEO
Ac
O
Ac
O
=
+
−+
+
−=−=
;
4
2
11
22
1
l
l
AOHO ===
;
( ) ( )
5
2
1
2
1
)()( lzzzxxxOHODHD
OADOAD
=−−+−−=−=
;
( ) ( )
6
2
1
2
111
lzzxxOEOOEO
DODO
=−+−=−=
;
ψ
ψτ
ψ
θ
sin2
)sin(
sin
sin
2
11
+
==
l
HOFO
.
Значения углов в рассматриваемых треугольниках (см. рис.2,в) определяются из простых три-
гонометрических соотношений
−+
=
31
2
2
2
3
2
1
2
2
arccos
ll
lll
ϕ
;
−+
=
=
3
2
2
2
3
2
1
2
1
2
21
1
2
arccossinarcsin
sin
arcsin
ll
lll
l
l
l
l
ϕ
ϕ
;
12
180
ϕϕτ
−−=
;
−+
=
54
2
6
2
5
2
4
2
arccos
ll
lll
ψ
;
ψ
τ
θ
−
−
=
180
.
Треугольники BO
1
F и BEA подобны по трем сторонам, следовательно, коэффициент подобия
k может быть выражен через отношение длин пары соответствующих сторон, например, FO
1
и
AE:
)sin(
sin2
2
1
1
ψτ
ψ
+
==
l
l
FO
AE
k
. (8)
Длина медианы ВЕ треугольника АВС может быть найдена как сумма отрезков EO
1
и O
1
B:
)
1
1
(
1
3
3
3
−
+=
−
+=
k
ll
k
l
lBE
.
Тогда координаты вершины В треугольника АВС, которой соответствует вершина P
1
характе-
ристической ломаной сегмента Безье могут быть найдены как
2
2
1
32
sin)
1
)sin(
sin2
1
1()90cos(
ϕ
ψτ
ψ
ϕ
−
+
++=−+=
l
l
lxBExx
EFB
,
2
2
1
32
sin)
1
)sin(
sin2
1
1()90sin(
ϕ
ψτ
ψ
ϕ
−
+
++=−+=
l
l
lzBEzz
EEB
.
Секция 4. Сортопрокатное и волочильное производство
424
Величина полноты w
1
квадратичного сегмента Безье характеризуется отношением отрезков
медианы, получаемых при ее пересечении с кривой в точке максимума и может быть выражена
как
1
1
)1(
3
3
1
1
1
−
=
−
==
kkl
l
BO
EO
w
,
Подстановка в данное уравнение выражения (8) дает
1
)sin(
sin2
1
2
1
1
−
+
=
ψτ
ψ
l
l
w
. (9)
Аналогичным образом, определяются величины P
1
j
, w
1
j
других сегментов, составляющих
линии, ограничивающие участки прилегания носка проводки к валкам сверху (P
2
j
)
1
1
-(P
2
j
)
0
1
и сни-
зу (P
0
j
)
1
1
-(P
0
j
)
0
1
. Нетрудно убедиться, что эти вершины будут соответствовать вершинам характе-
ристических ломаных Q
3
j
и Q
5
j
(см. рис.1 и рис.4).
Чтобы задать поверхность, соответствующую участку прилегания носка проводки к валкам
осталось определить положение вершин Q
4
j
скелета и значений w
4
j
в каждой из них (см. рис.1).
Как уже отмечалось, каждой вершине скелета детали Q
i
j
соответствует отдельная порция по-
верхности вращения, которую в нашем случае следует обозначить P
kl
, где k соответствует номе-
ру сегмента кривой на верхней или нижней грани носка проводки, которые содержит указанная
порция, причем ее вершина совпадает с соответствующей вершиной скелета Q
4
j
(рис. 4,а).
Определение положения вершин характеристического скелета проводки
а-вершина участка прилегания носка; б-вершина участка скоса носка
Рис.4
Для Q
4
j
и w
4
j
требуется найти соответствующие им величины P
11
kl
, w
11
kl
у каждой порции по-
верхности. Граничной кривой каждой пары порций рассматриваемого участка носка проводки
является дуга окружности R
i
, концы которой P
01
kl
, P
21
kl
совпадают с одноименными концами сег-
ментов P
2j
и P
0j
, рассмотренных в предыдущем пункте. Положение вершин P
1j
kl
, в том числе и
вершины P
11
kl
, для k-порции будем определять для каждой пары одноименных точек характери-
стических ломаных P
2j
, P
1j
, P
0j
смежных сегментов, составляющих линию прилегания носка
проводки к ручью.
Величина угла ε
j
(см. рис. 4,а) равна

Секция 4. Сортопрокатное и волочильное производство
425
ε
j
= 90-ά
j
– β
j
,
где ά
j
и β
j
определяются по формулам (3), (7).
Длина отрезков P
0j
kl
, P
1j
kl
и P
01j
kl
, P
2j
kl
характеристической ломаной текущей дуги окружно-
сти радиуса R
j
равна e
j
e
j
= R
j
tg(ε
j
/2) .
Таким образом, координаты точки P
1j
kl
могут быть найдены как
x
1j
kl
= (x
0j
kl
+ x
2j
kl
)/2 ,
y
1j
kl
= y
0j
kl
+ ε
j
sinβ
j
,
z
1j
kl
= z
0j
kl
- ε
j
sinβ
j
.
Величина полноты w
10
kl
и w
12
kl
для граничных кривых порции равна синусу половины угла
при вершинах P
ij
kl
их характеристических ломаных [7]. Величина этого угла ω
j
составляет
ω
j
= 180 - ε
j
= 90 + ά
j
+ β
j
.
Таким образом, величины w
10
kl
и w
12
kl
можно выразить в виде формулы
w
1j
kl
= sin ω
j
= sin(90 + ά
j
+ β
j
) = -cos( ά
j
+ β
j
) ,
где j≠1.
Значения w
01
kl
и w
21
kl
и для характеристических ломаных, ограничивающие рассматриваемый
участок сверху и снизу, соответствуют величине w
1
, определяемой по формуле (9). Значение
полноты w
11
kl
в характеристической точке P
11
kl
порции, соответствующей вершине скелета Q
4
j
,
может быть определено как
w
11
kl
=w
4
= w
10
kl
·w
01
kl
,
где i=0,1,2 .
После подстановки в данную формулу предыдущего выражения и с учетом формулы (9) име-
ем
1
)sin(
sin2
)cos(
2
1
411
−
+
+
==
ψτ
ψ
β
α
l
l
ww
jj
jkl
. (10)
Построение скелета участка скоса носка проводки. Характеристическая ломаная Q
6
j
, опре-
деляющая скос носка, может быть получена перемещением характеристической ломаной Q
5
j
вверх на величину ∆y=h
2
и в сторону пяты на величину ∆z=l
c
, которая определяется величиной
радиуса скругления R
c
(см. рис.4, б). Для построения характеристической ломаной Q
6
j
необходи-
мо определить значение l
c
и величину полноты w
c
в местах сопряжения соседних порций скоса,
которая в рассматриваемом случае будет одинаковой во всех вершинах P
10
k2
и P
12
k2
.
Указанные величины определены с использованием простых геометрических и тригономет-
рических преобразований четырехугольника OCVA, образованного характеристической ломаной
дуги окружности в сечении скоса носка в месте сопряжения двух соседних порций и ограничи-
вающими ее радиусами R
c
.
c
c
c
R
hR
w
2
2
2
sin
2
−
=
=
β
, (11)
2
2
2
2
2
2
2
2
2
h
hR
hR
htl
c
c
c
−
−
=−=
. (12)
Параметры характеристической ломаной Q
6
j
, задающей скос носка проводки, выражаются
через параметры характеристической ломаной Q
5
j
с учетом (11) и (12) следующим образом:
Секция 4. Сортопрокатное и волочильное производство
426
x
6
j
= x
5
j
,
y
6
j
= y
5
j
+ h
2
,
z
6
j
= z
5
j
- l
c
= z
5
j
-
2
2
2
2
2
2
h
hR
hR
c
c
−
−
,
c
c
jj
c
j
R
hR
wwww
2
2
2
556
−
==
.
Положение остальных характеристических точек скелета фасонной проводки: Q
1
j
, Q
2
j
, Q
7
j
,
Q
8
j
может быть найдено по известным конструктивным размерам этой детали.
Таким образом, используя конструктивные размеры фасонной проводки и преобразуя харак-
теристический скелет сечения сопряженного с ней ручья, можно построить характеристический
многогранник для лекальных поверхностей ее носка, предназначенный для их дальнейшего по-
строения методом Безье.
Рассмотренная геометрическая модель послужила основой для дальнейшей разработки про-
граммы по расчету координат скелета носка фасонных проводок. В ней определение координат
характеристического каркаса лекальной поверхности носка осуществляется преобразованием ко-
ординат соответствующих точек сегментов кривых второго порядка и отрезков прямых плоского
контура ручья валка, сопрягающегося с проводкой. Математическая модель такого контура, соз-
данного с применением метода Безье была подробно рассмотрена в работах [7,8]. Созданный
программный модуль реализован на языке C++, работает в автономном режиме и обеспечивает
расчет и последующую распечатку координат точек скелета носка. Работа пользователя с про-
граммой сводится к заданию характеристического каркаса ручья валка, размеров, характеризую-
щих расположение проводки относительно ручья, визуальному контролю построенного контура и
распечатки результатов расчета. Разработанная программа была использована в процессе по-
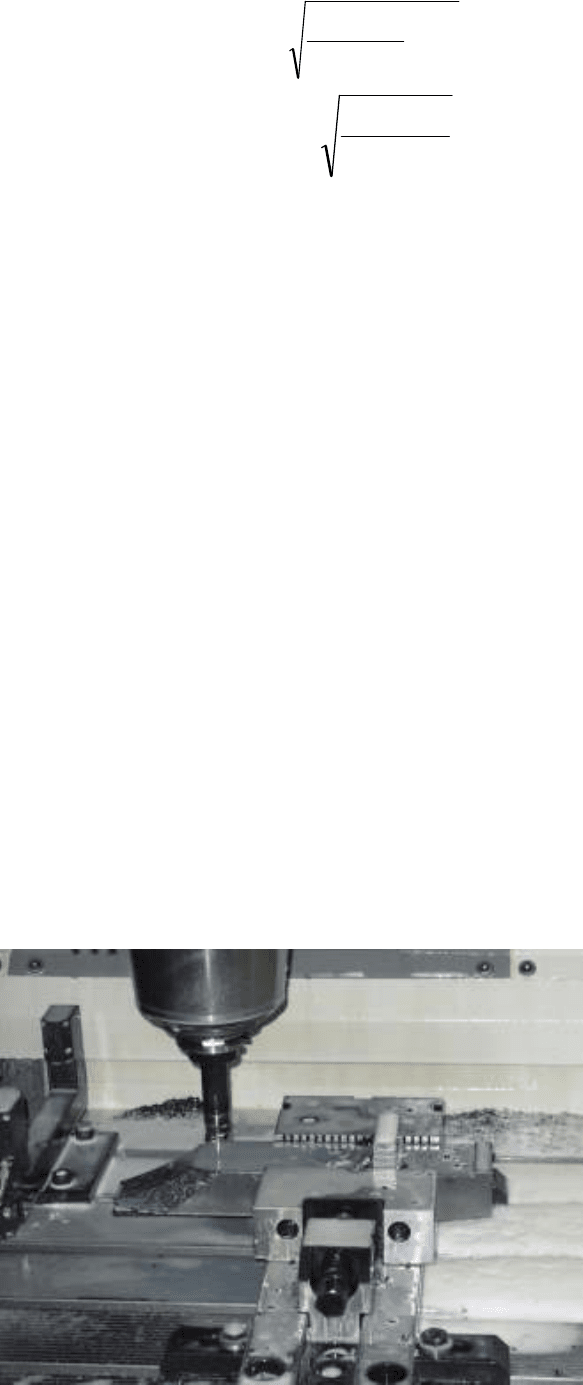
строения трехмерных моделей этих деталей, по которым Экспериментальным производственным
комбинатом УрФУ с применением станков типа обрабатывающий центр был изготовлен алюми-
ниевый макет проводки для ящичного калибра (рис.5), а затем произведена партия выводных
проводок для ОАО «Златоустовский металлургический завод» [9].
Изготовление выводной проводки для ящичного калибра на обрабатывающем центре
Рис.5
Секция 4. Сортопрокатное и волочильное производство
427
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1.Шенен П., Коснар М., Гардан И., и др.Математика и САПР. М.:Мир.1988. Т.1,2.
2.Фокс А., Пратт М. Вычислительная геометрия. Применение в проектировании и на произ-
водстве. - М.: Мир. 1982.302 с.
3. Сухих Б.И., Вайсбурд Р.А. Вычислительная геометрия. Основные объекты и преобразова-
ния. - Свердловск: УПИ.1989. 91 с.
4.Стародетко Е.А. Математическое моделирование лекальных поверхностей / Под ред.
П.М.Чеголина. - Минск: Наука и техника. 1984. 126 с.
5. Александров А.Д., Нецветаев Н.Ю. Геометрия. М.:Наука.1990. 672 с .
6.
Берже М. Геометрия М.:Мир.1984. Т.1,2.
7.Слукин Е.Ю., Шилов В.А. Моделирование формы калибров в системах проектирования тех-
нологии сортовой прокатки /Изв. вузов. Черная металлургия. 1991. N 4. с. 37-39.
8. Слукин Е.Ю., Шилов В.А. Алгоритм и программа автоматизированного построения калиб-
ров произвольной формы / Изв. вузов. Черная металлургия. 1991. N 6. с. 36-38.
9.
Слукин Е.Ю., Гайсин Н.В. Особенности изготовления выводных проводок сортовых станов
на многооперационных станках в УГТУ-УПИ. / Изв. вузов. Черная металлургия. 2010. N 3.
с.65-66.

Секция 4. Сортопрокатное и волочильное производство
428
ОПРЕДЕЛЕНИЕ СЕЧЕНИЙ НЕПРЕРЫВНО ЛИТЫХ ЗАГОТОВОК ДЛЯ ОБЕСПЕЧЕНИЯ
ВЫСОКОГО КАЧЕСТВА ГОРЯЧЕКАТАНОЙ СТАЛИ
Трайно А.И.
ИМЕТ им. А.А. Байкова РАН traino@aport.ru
В настоящее время нет единого мнения о минимально допустимой вытяжке (размере возмож-
ного сечения) непрерывно литой заготовки при прокатке сортовых профилей из шарикоподшип-
никовых, конструкционных и легированных марок сталей, обеспечивающей качественную прора-
ботку литой структуры, устранение осевой шнуровидной ликвации. Поэтому после ввода в экс-
плуатацию сортовой МНЛЗ проведены работы по исследованию формирования структуры сорто-
вой полосы, заготовкой для которых является литой квадрат 150 и 100 мм, в клетях сортопрокат-
ных станов. На отобранных темплетах исследовали балл карбидной сетки, центральную порис-
тость, осевую ликвацию, ликвационные полоски и трещины, осевые, угловые, светлые полоски и
краевые точечные загрязнения. С использованием микроструктурных исследований подтвержде-
но, что увеличение степени деформации улучшает проработку структуры литой заготовки и спо-
собствует повышению комплекса механических свойств для всего марочного сортамента. В ре-
зультате анализа экспериментальных данных определены минимально допустимые вытяжки,
обеспечивающие формирование бездефектной структуры готовых сортовых профилей. Обобщен-
ные результаты исследований представлены эмпирическими уравнениями (1)-(3), описывающими
взаимосвязь минимально допустимой вытяжки и размера исходной непрерывно литой заготовки
из различных марок сталей.
Для углеродистых качественных, низколегированных сталей:
S
max
= 14,24x
2
+ 257,7x + 1154. (1)
Для металлокорда, канатных сталей:
S
max
= 9,07x
2
+ 163,3x + 735. (2)
Для пружинных, шарикоподшипниковых сталей:
S
max
= 6,93x
2
+ 122,9x + 565. (3)
где S
max
-максимально допустимая площадь поперечного сечения
сортового профиля;
1
10
100
+
−
=
a
x
;
а – сторона квадрата непрерывнолитой заготовки, в мм;
Из этих уравнений следует, что минимальная кратность при прокатке конструкционных каче-
ственных сталей составляет 7, канатных сталей 11, шарикоподшипниковых 15.
Проведенные исследования позволили уточнить сортамент профилей, прокатываемый из ли-
той и перекатной заготовки на станах 350, 250 и 150 в зависимости от химического состава и на-
значения готового проката.
Теоретически возможный сортамент, выкатываемый из литой заготовки квадрат 100 мм, для
станов 250 и 150 представлен в таблице 1.
Из таблицы 1 следует, что из заготовки квадрат 100 мм может быть получен только сортовой
прокат мелких сечений. Поэтому для расширения размерного сортамента профилей было предло-
жено организовать в черновой группе клетей стана 350 производство перекатной заготовки квад-
рат 100 мм из непрерывно литой заготовки квадрат 150 мм.
Теоретически возможный сортамент для станов 250 и 150, выкатываемый из заготовки квад-
рат 150 мм после ее переката в заготовку квадрат 100 мм, представлен в таблице 2.
Таблица 1.

Секция 4. Сортопрокатное и волочильное производство
429
Сортамент станов 250 и 150 при использовании непрерывно литой заготовки
Тип стали
Максимально возможная площадь готового профиля и
выкатываемый профиль
Шарикоподшипниковые
667
мм
2
круг 30
Легированные, канатные, ме-
таллокорд
889
мм
2
квадрат 30, круг 34, уголок 75х6
Конструкционные качественные
1410
мм
2
квадрат 37,5 мм, круг 42 мм, уголок
90х8, швеллер №12
Таким образом, предложенный подход позволил определить минимально допустимые вытяж-
ки для качественных марок сталей и расширить размерный сортамент профилей, прокатываемых
как из литых, так и перекатаных заготовок на станах 250 и 150.
Таблица 2.
Сортамент станов 250 и 150 при использовании непрерывно литой
и перекатной заготовки
Тип стали
Максимально возможная площадь готового профиля и
характерный профилеразмер
Шарикоподшипниковые
1500
мм
2
круг 44
Легированные, канатные, ме-
таллокорд
2000
мм
2
квадрат 44, круг 50, уголок 125х8
Конструкционные качественные
3170
мм
2
квадрат 56, круг 63, уголок 160х10, швеллер №24
В результате исследований определена оптимальная схема деформирования (схема I), при ис-
пользовании которой обеспечивается равномерная деформация по клетям, хорошая прорабатывае-
мость структуры и наименьшая вероятность образования дефектов на поверхности полосы. Данная
схема обеспечивает при производстве перекатной заготовки для станов 250 и 150 примерно рав-
номерную вытяжку в калибрах горизонтальных клетей.
Схема I
деформирования при получении квадрата 100 мм и 125 мм из литой
заготовки квадрат 150
Квадрат 150 →кантовка на ребро → проход 1 (λ=1,17) → кантовка на 90º → проход 2 (λ=1,07) →
проход 3 (λ=1,19) → {квадрат 125} → проход 4 (λ=1,27) → проход 5 (λ=1,21) → квадрат 100.
Преимуществом данной схемы является возможность получения квадрата 125 мм после 3-го
прохода (перекатная заготовка для производства некоторых видов профилей). Однако эта схема по
условиям загрузки четвертой клети оказалась применима только для рядовых и малоуглеродистых
сталей из-за недостаточной мощности и жесткости этой клети.
В результате проведенных исследований для прокатки труднодеформируемого сортамента из
шарикоподшипниковых и пружинных марок сталей было рекомендовано реконструировать чет-
вертую вертикальную клеть. При этом может быть реализована схема прокатки II.
Схема II
