Сборник - Тезисы конференции Геомодель - 2011
Подождите немного. Документ загружается.

«Геомодель – 2011» - 13ая конференции по проблемам комплексной
интерпретации геолого-геофизических данных.
Россия, г. Геленджик, 11 – 15 сентября, 2011 г.
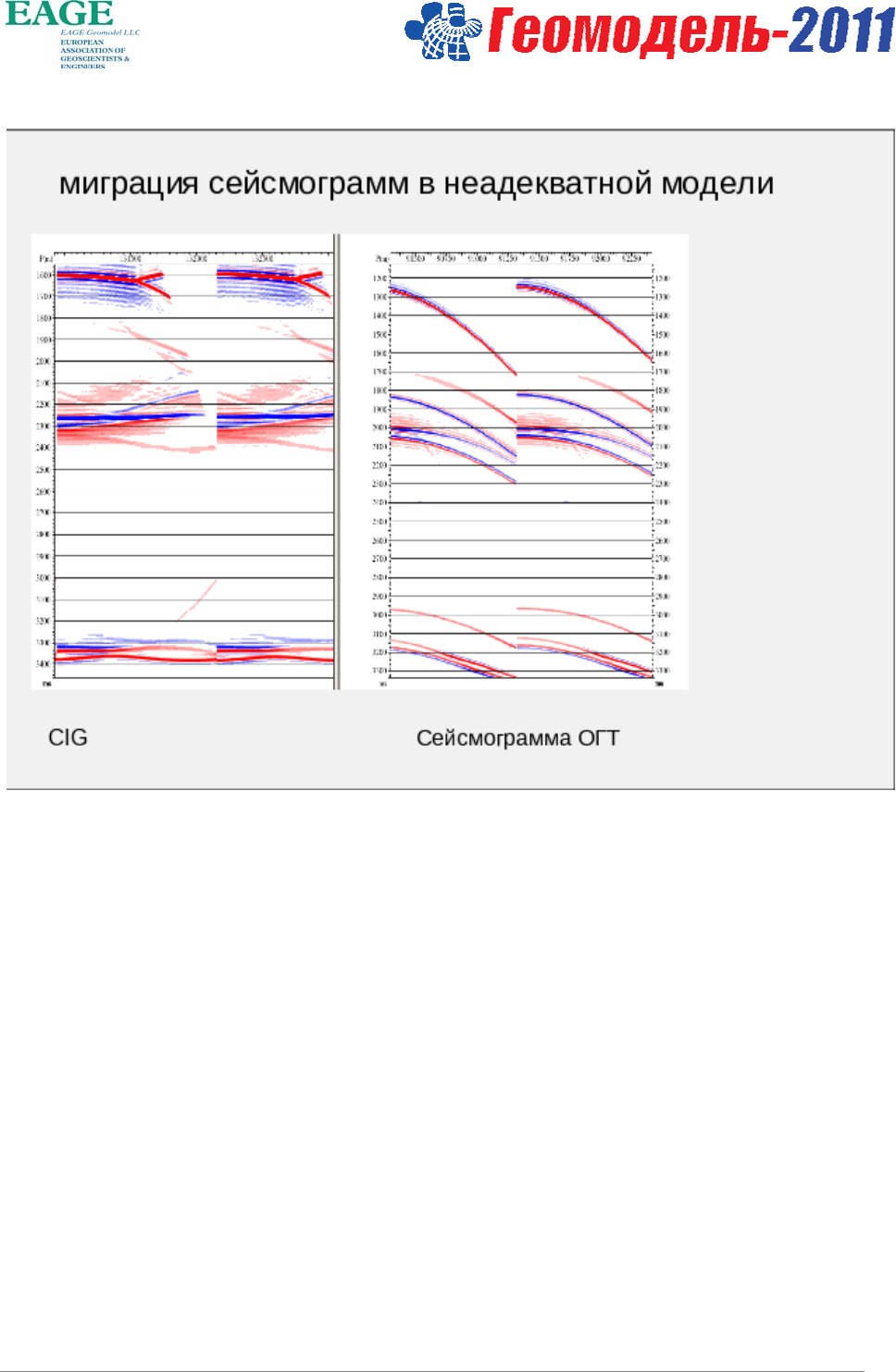
Рисунок 2.
Кинематико-динамическое преобразование, предложенное в 70-е годы Глоговским и соавторами,
было придумано для корреляции (прослеживания) сложных синфазностей. Делалась миграция в
простой модели среды, прослеживание границы на результате миграции и решалась прямая
кинематическая задача в этой модели среды. Примерно такая же схема предлагается для
прослеживания годографов отраженных волн,
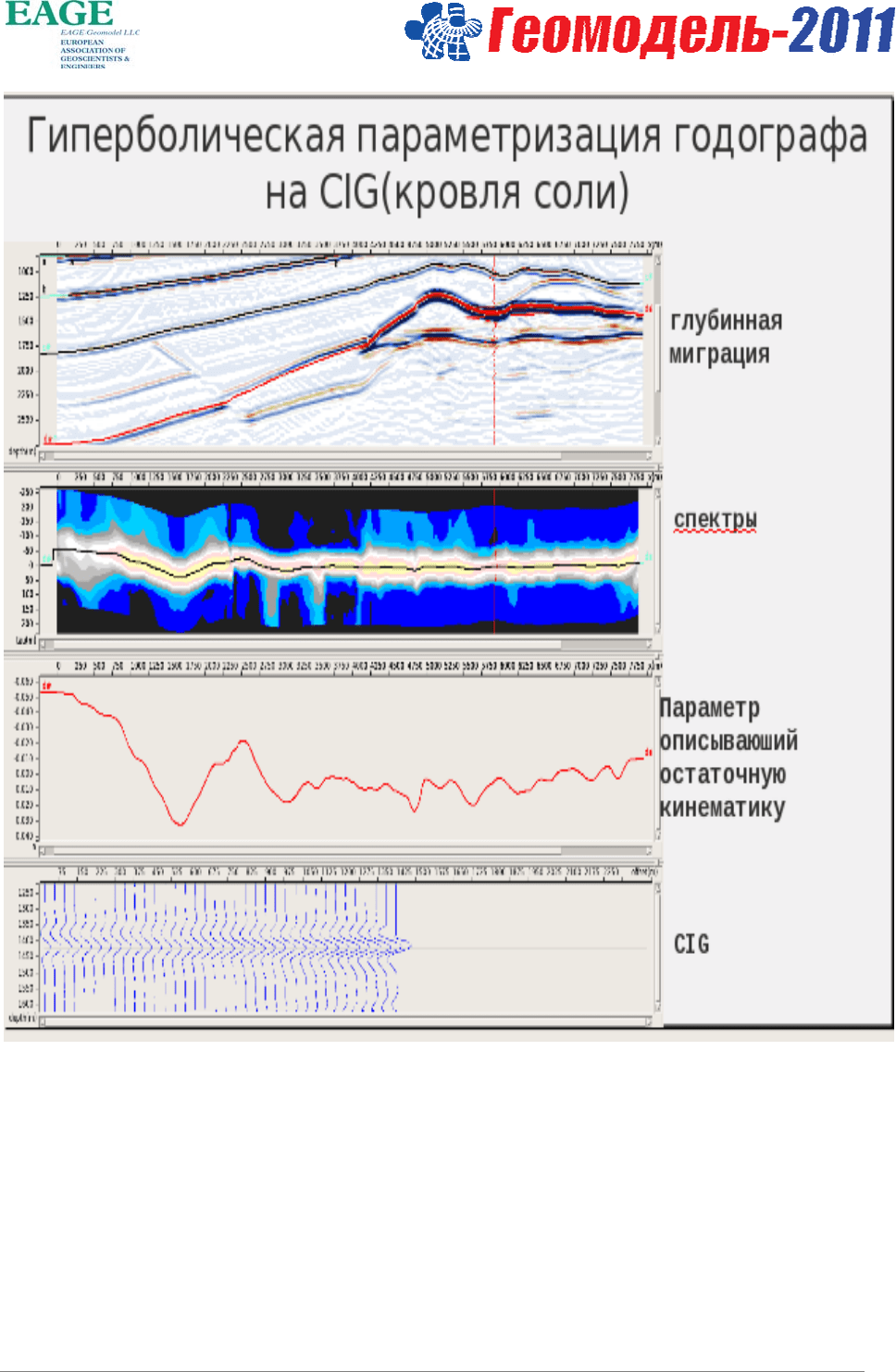
хотя теперь это уже миграция сейсмограмм, а
прослеживание границ для разных моделей среды производится по сейсмограммам общей точки
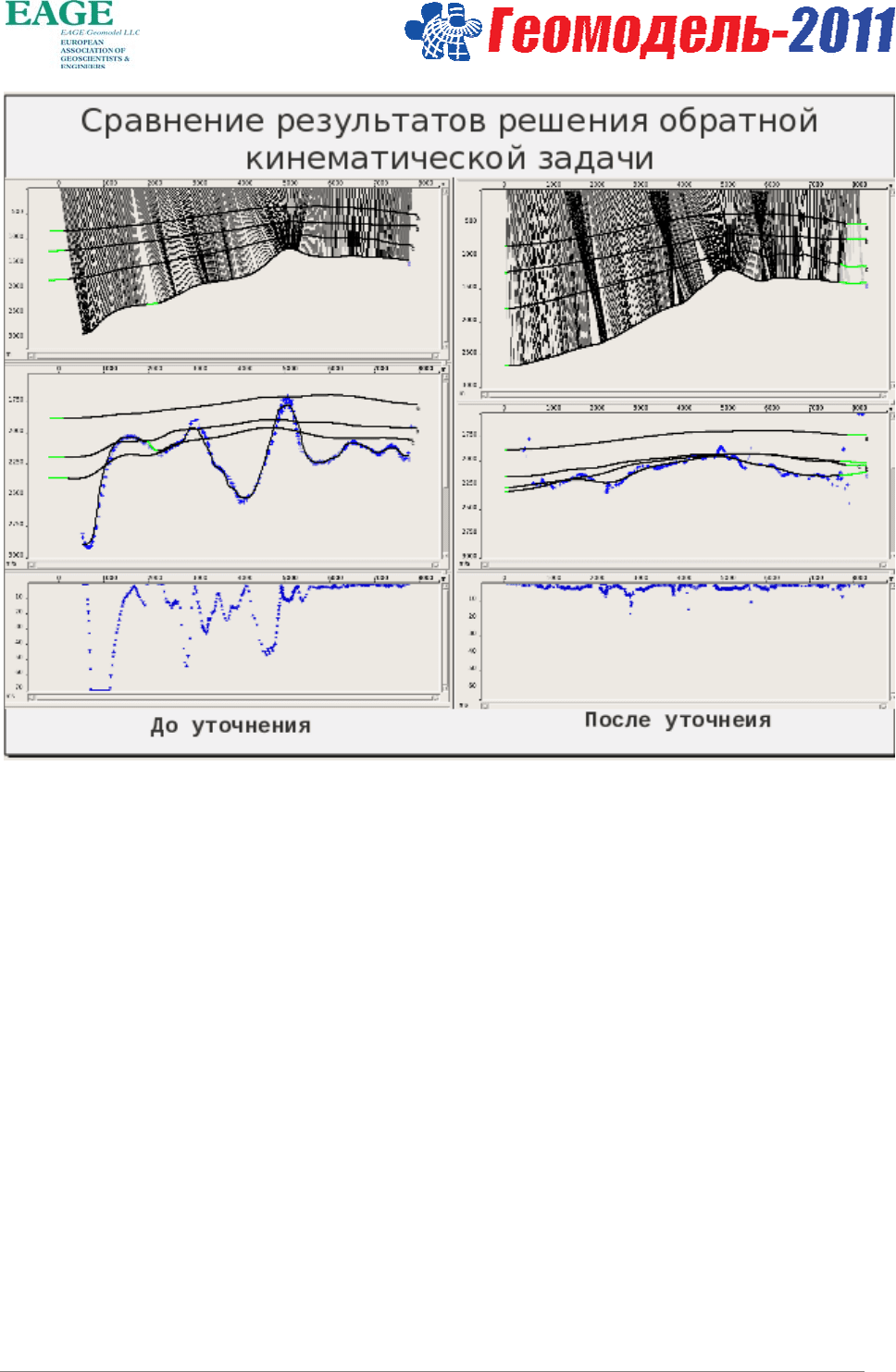
изображения. (Рис.3) Полученное таким образом поле времен используется для решения обратной
кинематической задачи. (Рис. 4)
«Геомодель – 2011» - 13ая конференции по проблемам комплексной
интерпретации геолого-геофизических данных.
Россия, г. Геленджик, 11 – 15 сентября, 2011 г.
Рисунок 3.
«Геомодель – 2011» - 13ая конференции по проблемам комплексной
интерпретации геолого-геофизических данных.
Россия, г. Геленджик, 11 – 15 сентября, 2011 г.
Рисунок 4.
Обсуждаемый подход делает возможной и непротиворечивой полную обработку сейсмических
данных на основе пластовой модели среды.
«Геомодель – 2011» - 13ая конференции по проблемам комплексной
интерпретации геолого-геофизических данных.
Россия, г. Геленджик, 11 – 15 сентября, 2011 г.
СРАВНИТЕЛЬНАЯ ХАРАКТЕРИСТИКА ИНВЕРСИОННЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ
КАРБОНАТНО-ТЕРРИГЕННЫХ ГЕОЛОГИЧЕСКИХ СРЕД.
Сиротенко Д.О.* (ООО “ЛАРГЕО”), Мясоедов Д.Н. (ООО “ЛАРГЕО”)
Сервисные и нефтяные компании в настоящее время обладают богатым арсеналом средств
программного обеспечения (ПО) для выполнения инверсионных преобразований сейсмической и
скважинной информации. Однако, при работах в районах со сложным геологическим строением
все
более актуальной становится задача тестирования данного ПО с целью определения экономически
обоснованных режимов его эксплуатации. Теоретические вопросы анализа алгоритмов инверсии
рассмотрены Гогоненковым (1987), Doyen (2007), Sams and Saussus (2010). Результаты
сравнительного анализа алгоритмов публиковались значительно реже (Neep 2008). В настоящей
работе представлены результаты сравнения эффективности различных алгоритмов инверсии для
карбонатно-терригенных разрезов Среднего Поволжья.
Краткая сейсмогеологическая характеристика района работ
Геологический разрез района работ можно разделить на 7 основных комплексов (в скобках дана
геологическая индексация): преимущественно карбонатный (P1kng-C2vr); преимущественно
терригенный (C2vr-C2b); преимущественно карбонатный (C2b-C1tr); преимущественно карбонатный
(C1tr-C1bb); преимущественно терригенный (C1bb-C1t); преимущественно карбонатный (C1t-D3tm);
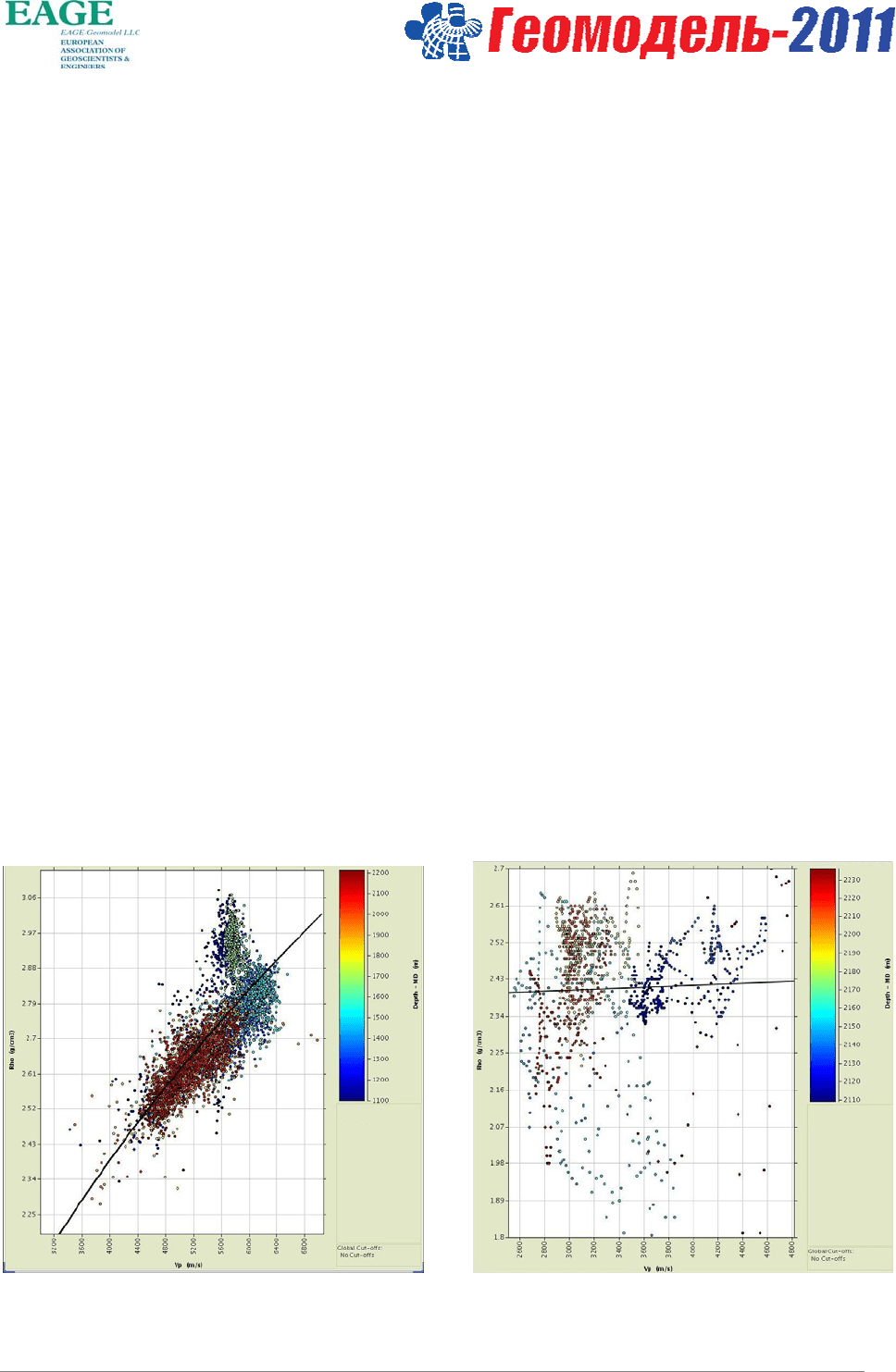
преимущественно терригенный (D3tm-AR). На рисунке 1 представлены графики зависимостей
“плотность/скорость продольных волн” для преимущественно карбонатного (P1kng-C2vr) и
преимущественно терригенного (C2vr-C2b) комплексов. При оценке эффективности инверсионных
преобразований
используются количественные оценки, сделанные, как для всего интервала расчета
инверсии (P1kng-AR), так и для трех основных преимущественно карбонатных комплексов пород (L1
- C2b-C1tr; L2 - C1tr-C1bb; L3 - C1t-D3br).
Одной из основных особенностей района работ является чрезвычайно малое количество поисковых
скважин. Данное обстоятельство, упрощает проверку эффективности инверсионных алгоритмов, но, с
другой стороны, сильно осложняет проведение последующего статистического анализа сейсмических
атрибутов.
а) б)
Рисунок 1. Графики зависимости “плотность/скорость продольных волн” для преимущественно
карбонатного а) и преимущественно терригенного б) интервалов геологического разреза.
«Геомодель – 2011» - 13ая конференции по проблемам комплексной
интерпретации геолого-геофизических данных.
Россия, г. Геленджик, 11 – 15 сентября, 2011 г.
Характеристика алгоритмов инверсионных преобразований
В настоящее время в индустрии эксплуатируются инверсионные алгоритмы двух категорий:
детерминистические и стохастические (Kemper 2010). Neep (2008) опубликовал результаты
сравнительного анализа алгоритмов инверсии до суммирования (prestack AVO inversion)
специальным образом подготовленного модельного куба данных, однако, не предоставил
информацию о математической основе тестируемых алгоритмов.
В работе приведены результаты сравнительного анализа 4 детерминистических алгоритмов инверсии
(coloured inversion - DET A; алгоритм,
реализующий анализ матрицы свертки - DET C; алгоритм,
использующий метод линейного программирования - DET L; sparse spike inversion - DET S) и одного
алгоритма стохастической инверсии (STOCH ST). При стохастической инверсии рассчитывалось 5
равновероятных реализаций куба акустического импеданса, окончательный результат –
арифметическое среднее всех полученных реализаций. Исходный сейсмический материал для всех
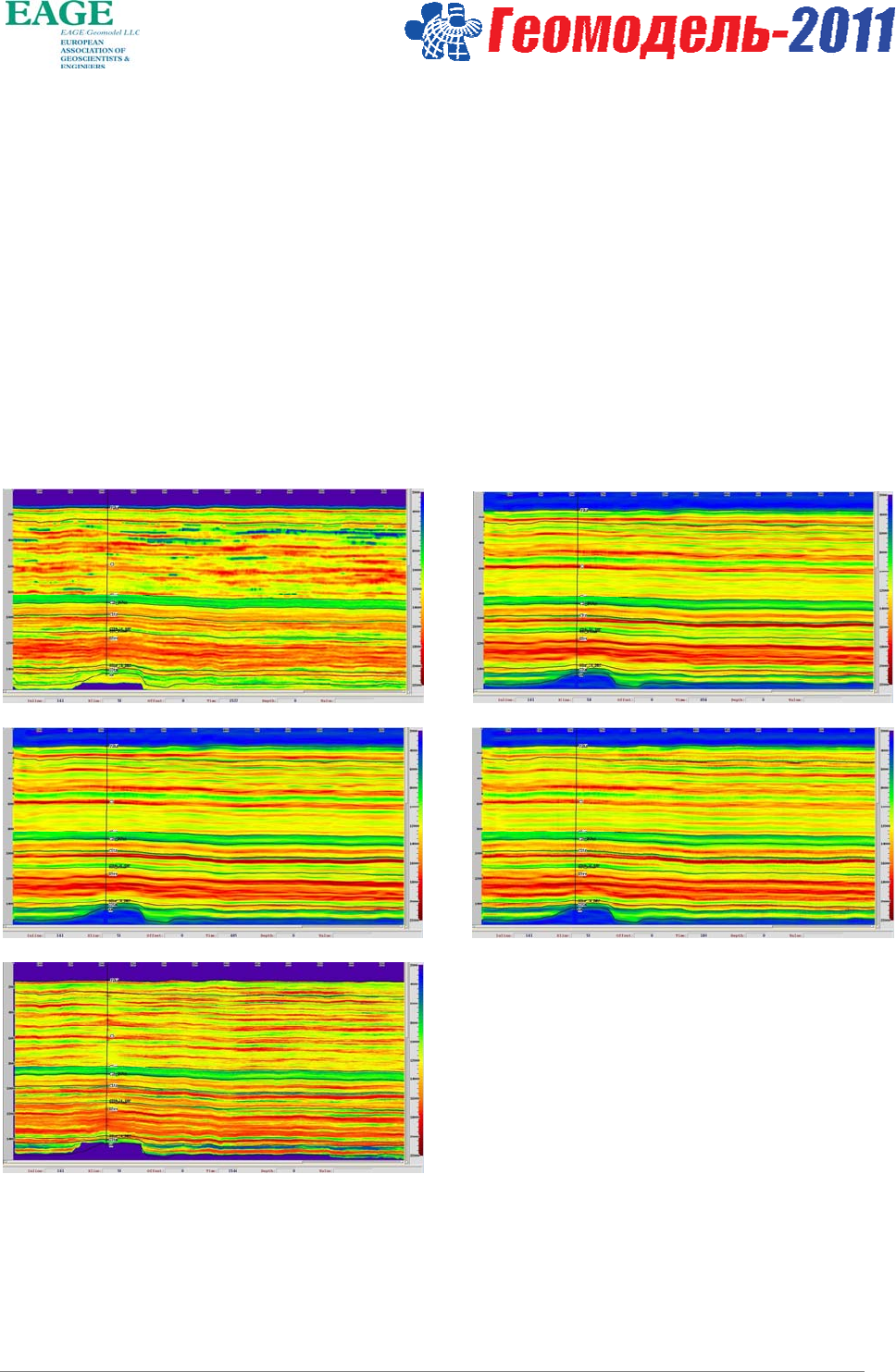
алгоритмов – куб данных, базовый для структурной интерпретации. На рисунке 2 показаны разрезы
акустического импеданса AI, полученные с помощью
применения указанных выше алгоритмов.
а) б)
в) г)
д)
Рисунок 2. Разрезы импеданса AI, полученные с помощью алгоритмов инверсии: а) DET A; б) DET C;
в) DET L; г) DET S; д) одна реализация стохастического алгоритма STOCH ST.
Методика оценки эффективности алгоритмов инверсии
Как известно, инверсионные преобразования работают как с сейсмической, так и с петрофизической
(каротажной) информацией. Следовательно, методика сопоставления результатов работы разных
«Геомодель – 2011» - 13ая конференции по проблемам комплексной
интерпретации геолого-геофизических данных.
Россия, г. Геленджик, 11 – 15 сентября, 2011 г.
алгоритмов должна включать оценку эффективности преобразования как сейсмических, так и
петрофизических данных. Показано (Sirotenko 2009) , что увеличение “сейсмической эффективности”
инверсии сопровождается уменьшением ее “петрофизической эффективности” инверсии и наоборот.
В данной работе точность восстановления как сейсмической, так и скважинной информации при
инверсии проверяется в точках заложения скважин. Данную процедуру предлагается называть 1D
проверкой. Выполняя 1D проверку
, мы, с одной стороны, сравниваем значения импеданса в скважине
со значениями импеданса, полученными в результате инверсии (эти значения экстрагируются из
рассчитанных кубов импедансов AI). С другой стороны, мы оцениваем меру сходства двух
сейсмических трасс: одной - экстрагированной из исходного сейсмического куба и другой -
рассчитанной с помощью свертки сейсмического импульса c трассой коэффициентов отражения
(получаемой из рассчитанных кубов импедансов AI с помощью известного соотношения RC(t) =
0.5*d[LnAI(t)]).
Метод перекрестной проверки (cross validation) использовался для оценки устойчивости решений
обратной задачи. Данный метод известен в геофизике под названием “blind test”. Его суть –
сравнение результатов инверсионных преобразований, выполненных как для всего множества
скважин, так и для контрольных выборок скважин. В качестве контрольной выборки при каждом
прогоне инверсии рассматривается исходное множество скважин с изъятием конкретной скважины.
На рисунках 3, 4 приводятся диаграммы, иллюстрирующие результаты 1D проверки эффективности
работы тестируемых алгоритмов инверсии.
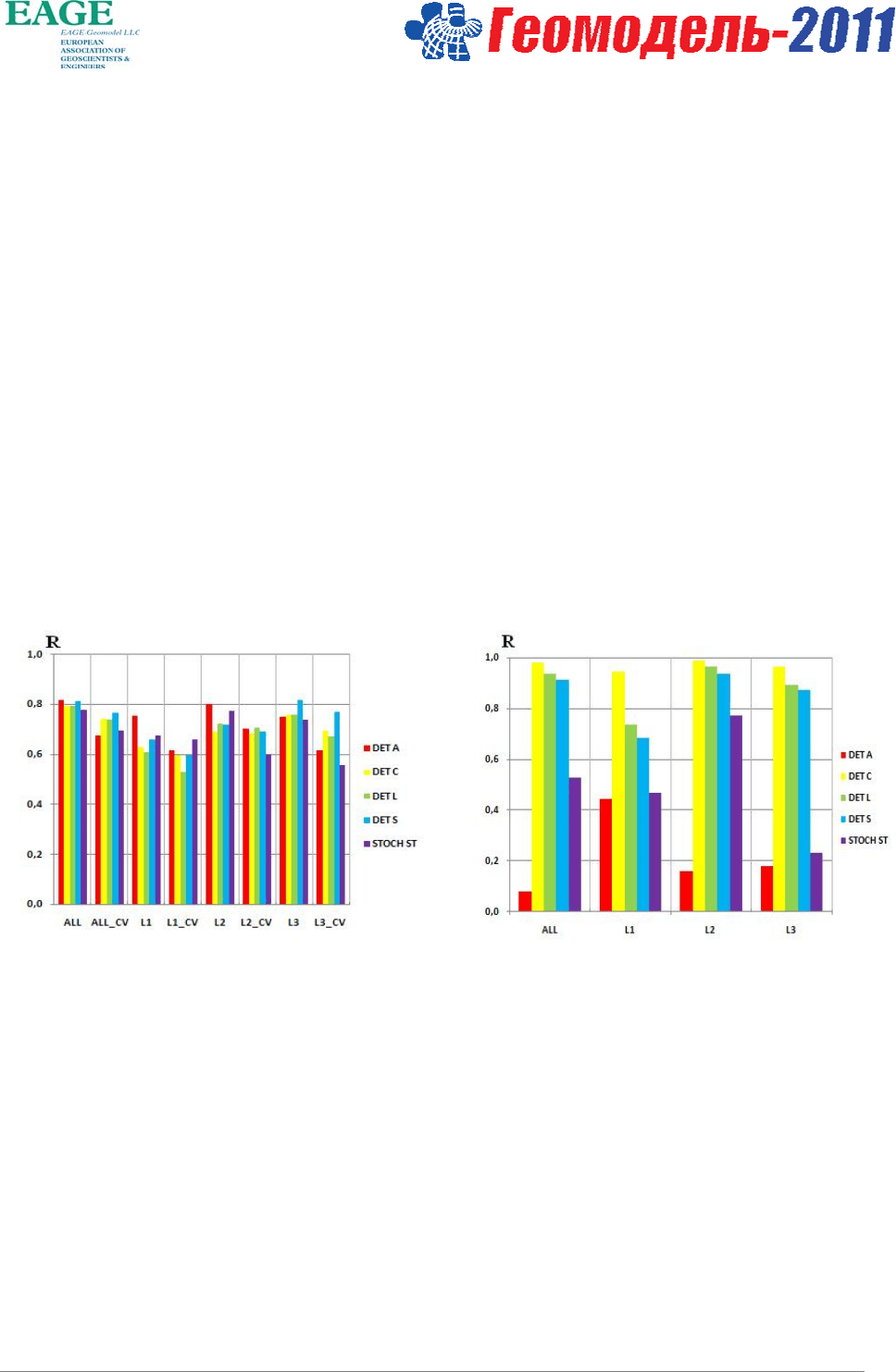
Рисунок 3 (слева). Коэффициенты корреляции между значениями импедансов AI, полученными с
помощью разных алгоритмов инверсии и исходными значениями AI для всего разреза ALL и пластов
L1-L3. Результаты перекрестной проверки показаны с индексом CV.
Рисунок 4 (справа). Коэффициенты корреляции между синтетическими трассами, полученными из
кубов импедансов AI, и исходными сейсмическими трассами для всего разреза ALL и пластов L1-L3.
Была осуществлена
проверка геологической адекватности результатов, полученных с помощью
разных алгоритмов инверсии. Общеизвестно, что существует обратная корреляционная связь между
коэф. пористости Кп и импедансом AI. Для каждого рассматриваемого карбонатного интервала было
получено уравнение регрессии типа Кп = f(AI). Данное уравнение использовалось для расчета
значений Кп с помощью экстрагированных из соответствующих кубов значений импеданса AI.
Рассчитанные по регрессии
значения Кп сравнивались со значениями Кп, полученными по
скважинным данным. Распределение ошибок при оценке величин Кп по результатам работы разных
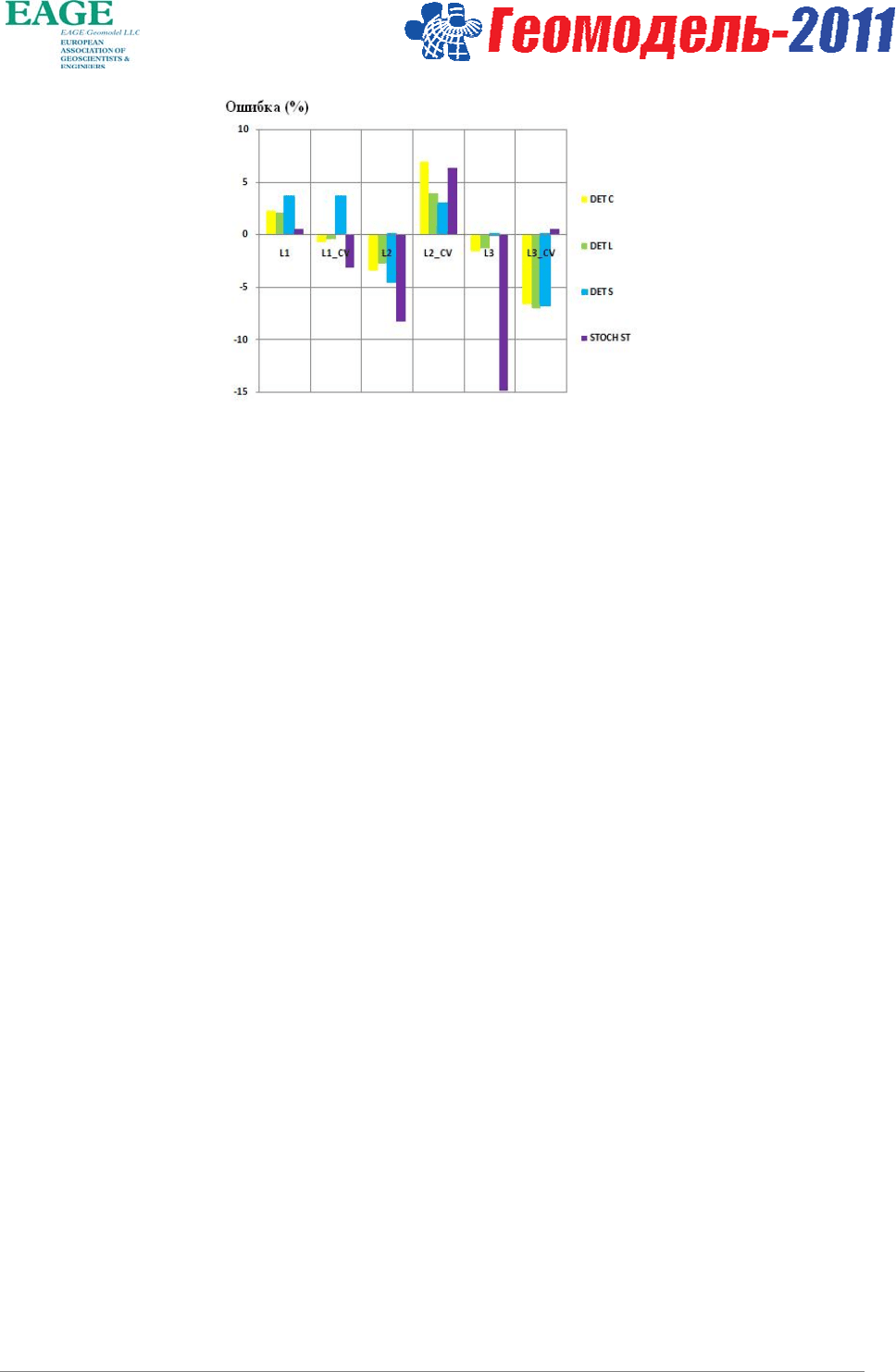
алгоритмов инверсии показано на рисунке 5. Положительная ошибка свидетельствует о недооценке
(underestimation) величины Кп по результатам инверсии, а отрицательная ошибка - о ее переоценке.
«Геомодель – 2011» - 13ая конференции по проблемам комплексной
интерпретации геолого-геофизических данных.
Россия, г. Геленджик, 11 – 15 сентября, 2011 г.
Рисунок 5. Ошибка восстановления значений Кп по результатам работы алгоритмов инверсии.
Анализ полученных результатов и некоторые выводы
Как следует из анализа данных, приведенных на рисунке 3, значения импеданса AI,
экстрагированные из кубов AI, полученных в результате работы каждого тестируемого алгоритма,
довольно сильно коррелируют со значениями AI в скважинах для всего карбонатно-терригенного
разреза (величины коэф
. корреляции порядка 0.8). Уменьшение величины коэф. корреляции,
зафиксированное по результатам перекрестной проверки не достигает критического значения R=0.5,
что позволяет говорить об устойчивости работы всех тестируемых алгоритмов инверсии.
Результаты восстановления сейсмической информации при инверсии (рисунок 4) показали
значительно больший разброс величин, чем результаты восстановления петрофизической
информации (рисунок 3). Отметим невысокое качество восстановления сейсмики по результатам
работы стохастического алгоритма. Неудовлетворительное качество восстановления сейсмики при
использовании алгоритма “сoloured inversion” свидетельствует о несоответствии стационарной
модели рядов RC(t), используемой в этом алгоритме, условиям реальных карбонатно-терригенных
геологических
сред.
Точность оценки величин Кп по результатам разных алгоритмов инверсии (фактически точность
оценки Кп только по одному сейсмическому атрибуту AI) для карбонатно-терригенных сред в целом
находится в пределах 5-10%, что само по себе неплохо и открывает большие перспективы для
применения множественного регрессионного анализа при динамическом анализе сейсмических
данных.
Литература
1. Doyen P.M. 2007. Seismic reservoir characterization. An Earth modelling perspective.
EAGE.
2. Kemper M. 2010. Rock physics driven inversion: the importance of workflow. First Break 28, 10, 69-
81.
3. Neep J.P. 2008. Benchmarking prestack AVO inversion. 70
th
EAGE meeting, Rome, Italy, Expanded
Abstracts, 1009.
4. Sams M. and Saussus D. 2010. Comparasion of lithology and net pay uncertainty between
deterministic and geostatistical inversion workflows. First Break 28, 2, 35-44.
5. Sirotenko D. 2009. The log correlation, wavelet extraction and prewhitening estimation – key
components of simultaneous inversion: an example from Western Siberia. SEG Expanded Abstracts
28, 2501-2505.
6. Гогоненков Г.Н. 1987. Изучение детального строения осадочных толщ сейсморазведкой. Недра,
Москва.

«Геомодель – 2011» - 13ая конференции по проблемам комплексной
интерпретации геолого-геофизических данных.
Россия, г. Геленджик, 11 – 15 сентября, 2011 г.
ПРОГНОЗ СКОРОСТНОЙ МОДЕЛИ РАЗРЕЗА ПО ДАННЫМ ГИС
Давыдова О.П.,* Городнов А.В., Черноглазов В.Н (РГУ нефти и газа имени И.М. Губкина)
Предложена методика моделирования кривой акустического каротажа (АК) по радиоактивным и
электрическим методам. Отличие данного подхода восстановления кривой акустического каротажа
заключается в комплексном учете петрофизических параметров пород, скважинных условий и
термобарических условий залегания на показания радиоактивных и электрических методов. Данный
алгоритм справедлив как для терригенных, так и для карбонатных отложений. На
тестовой скважине
выполнено сравнение результатов расчета по предлагаемой методики с результатами получаемыми
по известным методикам Фауста, Салема, Дворкина.
Для применения современных способов инверсии сейсмических данных, построения геоакустических
разрезов (расчета синтетических сейсмотрасс) требуется информация об акустических свойствах
пород по максимальному количеству скважин на месторождении. К сожалению, акустический метод
регистрируется в единичных
скважинах и, зачастую, только в продуктивной части разреза, поэтому
зарубежными и отечественными исследователями предпринимались многочисленные попытки
восстановления кривых акустического метода по другим методам ГИС.
Первая попытка восстановления скорости продольной волны по данным электрического каротажа
была предпринята Фаустом в 1953 г [4], который предложил эмпирическое уравнение:
6/1
⎟
⎠
⎞
⎜
⎝
⎛
=
Rw
Rt
ZVp
γ
, (1)
где γ = 2.2888 , Z - глубина в км, Rt и Rw – соответственно сопротивление породы и пластовой воды.
Модель Фауста справедлива только для сцементированных песчаников при изменении пористости от
5 до 20 %
С тех пор предпринимались многочисленные попытки модернизировать это уравнение. Известны
работы: Салем (2001), Дворкин и Нур (2006) [4]. Общей чертой моделей является попытка связать
скорость упругих волн в
породах только лишь с их электрическими свойствами. Модели справедливы
только для коллекторов с низким содержанием рассеянной глинистости.
Широко известна модель Л. Раймера (1980) [4] Ряд исследователей отмечает [3], что эмпирический
метод Раймера имеет ряд ограничений, связанных с однородностью породы, характером уплотнения
и цементацией, а также значением геометрического фактора пор.
Оригинальный подход предложили С.
Хью и Р.Вайт [5], развивая теорию эффективных сред для
песчано-глинистой модели породы. В этой модели скелет породы представлен смесью зерен песка и
частичками глин, для которой согласно теории Кастера-Токсеза (1974) рассчитываются упругие
модули скелета «сухой» породы. Затем, используя модель Гассмана (1951), определяются скорости
продольной и поперечной волн для насыщенных сред.
Ограничением данного подхода является необходимость учета большого количества
петрофизических данных, таких как форма пор, выражаемая через аспектное отношение, упругие
модули отдельных компонент скелета и др. Эта модель успешно опробована ее авторами на
лабораторных образцах керна, но трудно реализуема на практике, поскольку исследователи в
большинстве случаев не обладают необходимым объемом петрофизической информации
по всему
разрезу скважины.
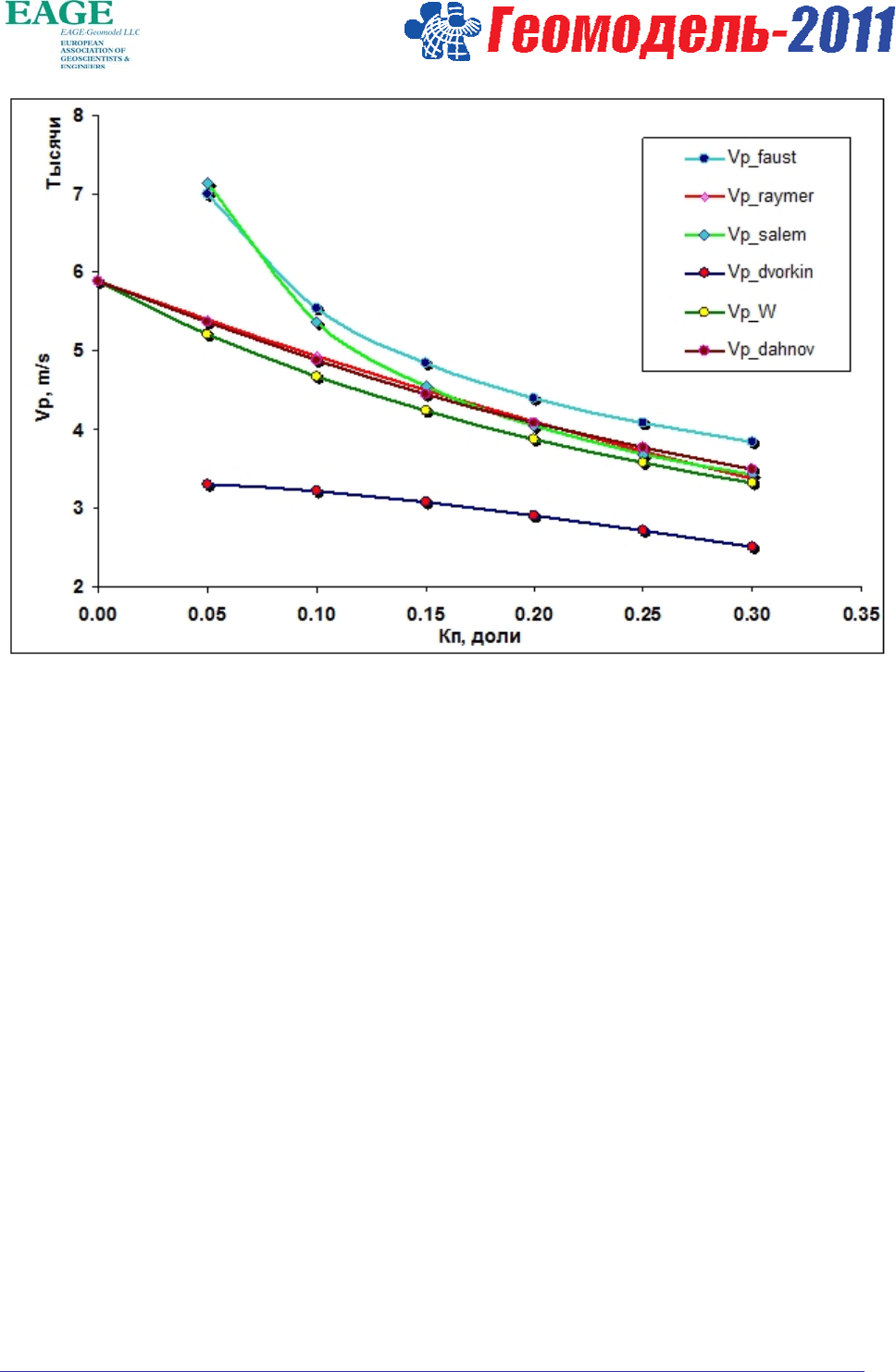
Результаты сравнения вышеперечисленных методик представлены на рисунке 1.
«Геомодель – 2011» - 13ая конференции по проблемам комплексной
интерпретации геолого-геофизических данных.
Россия, г. Геленджик, 11 – 15 сентября, 2011 г.
Рисунок 1 Зависимость Vp(Кп) для методик Фауста, Раймера, Салема, Дворкина, Вилли и Дахнова
Данные представленные на рисунке 1 были рассчитаны для сцементированного кварцевого
песчаника для следующих условий: глубина залегания пород 2500 м, скорость в матрице Vm = 5882
m/s, скорость в жидкости = 1640 m/s, коэффициент с = 0.3 (для уравнение Дворкина и Нура), фактор
сцементированности m = 2, фактор извилистости a = 0.81.
В настоящей работе
предлагается универсальная методика восстановления акустического метода как
для карбонатного, так и для терригенного разрезов. Методика принципиально отличается от
рассмотренных выше тем, что опирается на показания не одного, а нескольких методов ГИС и
одновременно учитывает изменение пористости, литологического состава, особенности уплотнения
глин с глубиной залегания, влияние термобарических условий на изменение свойств флюидов
и
других факторов. Учет особенностей уплотнения пород и термобарических условий особенно важен
при восстановлении кривой АК по всему разрезу скважин.
Минимальный комплекс методов ГИС для применения данной методики должен включать методы
естественной радиоактивности (ГК), нейтронный метод (НК), электрический метод (ИК или 2-х
метровый градиент зонд) и каверномер. Этот комплекс методов
является стандартным и обычно
регистрируется по всему стволу скважины.
Применение методики можно разделить на несколько последовательных этапов. На первом этапе
выполняется увязка кривых по глубине и литологическое расчленение разреза. По комплексу
радиоактивных и электрических методов в терригенном разрезе достаточно уверенно выделяются
пласты глин (аргиллитов), битуминозных глин, песчаников, плотных карбонатизированных прослоев
,
углей. В карбонатном разрезе по минимальному комплексу ГИС определяется компонентная
литологическая модель пород разреза.
Вторым этапом является определение водородосодержания (W) способом двух опорных пластов по
нейтронному методу, скорректированному за влияние скважины, и расчет коэффициента пористости

«Геомодель – 2011» - 13ая конференции по проблемам комплексной
интерпретации геолого-геофизических данных.
Россия, г. Геленджик, 11 – 15 сентября, 2011 г.
с учетом глинистости. Объемное содержание глинистых минералов определяется по гамма методу с
использованием эмпирической зависимости В.Ларионова.
Затем вычисляется пористость по электрическому методу. Предварительно вводятся поправки за
характер насыщенности коллекторов, за влияние скважины, а также учитывается зависимость
изменения сопротивления пластовой воды от температуры. Окончательно общая пористость пород
рассчитывается как средняя пористость
по нейтронному и электрическому методам.
Финальным этапом является расчет синтетической кривой АК по уравнению среднего времени,
предложенную В.Н.Дахновым [1] для глинистых пород:
()
(
)
ТтвТглКглТтвТфКпТтвТп
mm
Δ−Δ+Δ−Δ+Δ=Δ
21
, (2)
где ΔТп, ΔТтв, ΔТф, ΔТгл – интервальное время пробега продольной волны в породе, твердой фазе,
поровом флюиде и глине соответственно.
Показатели степени m1 и m2 отражают влияние структуры порового пространства и степени
цементации пород, изменяются в диапазоне 0.7-1.5, возрастая с увеличением уплотнения.
Интервальное время пробега продольной волны в поровом флюиде является функцией температуры,
давления и минерализации пластовой воды, изменяющихся по разрезу скважины. В пластах глин
(слоистая глинистость) изменение интервального времени ΔТгл с глубиной описывается законом
нормального уплотнения, который уточняется по данным АК в пластах глин по эталонной скважине.
Для песчаников с рассеянным типом глинистости интервальное время глин принимается равным
интервальному времени во флюиде.
Интервальное время в твердой фазе для карбонатного разреза определяется с учетом
многокомпонентного состава матрицы породы. Для однородных пачек солей, прослоев углей, пород
фундамента интервальное время породы задается постоянной величиной.
Предлагаемый метод был успешно апробирован на ряде месторождений (более 30 скв.), в том числе и
на месторождениях со сложными коллекторами. В качестве
примера, на рисунке 2 приведен
результат восстановления кривой АК для карбонатного разреза. Четвертый трек иллюстрирует
сопоставление зарегистрированной кривой DTp (зеленый цвет) и расчетной кривой DTp_calc
(красный цвет) по предлагаемой методике. На пятом треке показано сравнение записанной кривой
DTp и синтетической кривой DTp_фауст (черный цвет), полученной согласно уравнению Фауста,
голубой заливкой обозначен интервал расхождения кривых
.
