Сапожников А.А. Решение самостоятельных и контрольных работ по алгебре и началам анализа за 11 класс
Подождите немного. Документ загружается.

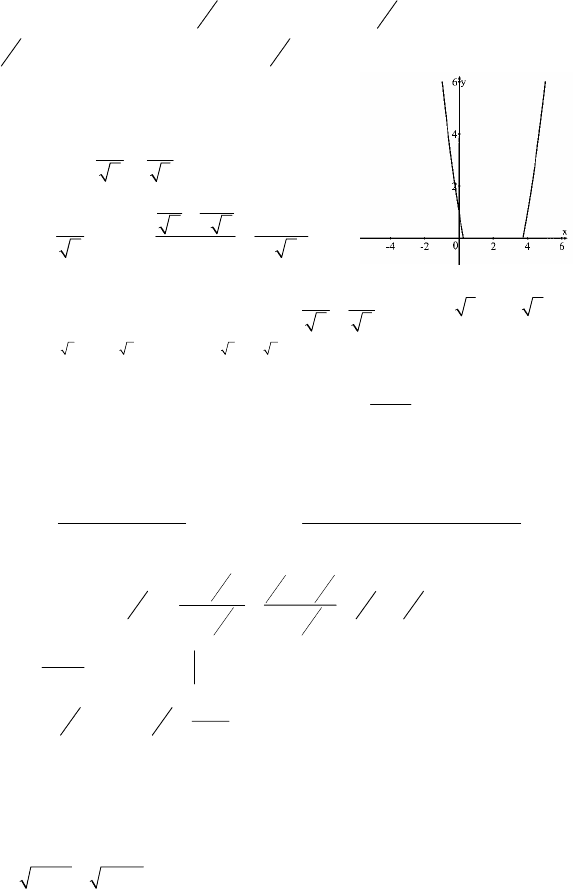
71
С–23
1.
222 2
333 3
() ( ) (2 3)
x
xxxxx xx
f х xe x e e x x e
−−− −′
′′
=+⋅ =+⋅−
=
2
3
x
x
e
−
(2х
2
–3х+1).
f'(x)=0 при x=1 и
1
2
x =
. f'(x)>0 при
1
2
x <
и x>1, f'(x)<0 при
1
1,
2
x<<
так что
min max
1
1, .
2
xx==
2.
(
)
2
3
log 4 1
3
xx
y
−+
= ; y=x
2
–4x+1 при
x
2
–4x+1>0 (см. график).
3. Сравним
ln 2
2
и
ln 3
3
. Для функции
() ()
1ln
ln 2 ln
2
:'
x
x
x
xx
fx f x
x
x
xx
−
−
===
.
f'(x)>0 при 0<x<e
2
. Так что f(x) – возрастает
при 0<
x<e
2
, так что f(2)<f(3), то есть
ln 2 ln 3
23
< , то есть
3ln2 2ln3<
или
32
ln 2 ln 3< , значит
32
23.<
4.
() ( )
2
212
x
x
fx x
−
=− . Первообразная
()
2
2
ln 2
xx
Fx C
−
=
+ .
С–24
1. а) f'(x)=(log
3
2
(x
3
+cosx))'=2log
3
(x
3
+cosx)⋅(log
3
(x
3
+cosx))'=
(
)
()
()
(
)
(
)
()
332
3
33
33
2log cos 2log cos 3 sin
cos ;
ln 3 cos ln 3 cos
x
xxxxx
xx
xx xx
++−
′
=⋅+=
+⋅+
б)
()
()
()
1
sin
cos
2
22
1
ln sin ctg
222
sin sin
22
x
x
x
x
fx
xx
′
′
′
====
.
2.
()
3
3
2
2
0
0
2
ln 1 ln10 ln1 ln10
1
x
dx x
x
=+=−=
+
∫
;
()
(
)
(
)
//
23
'1,5ln ln
f
xxx=−=
()
2
3ln
11
3ln 3ln 1 ln
x
x
xx
xx
x
=⋅− ⋅= −
; f'(x)=0 при x=1 и x=e. f'(x)>0 при
1<
x<e и f'(x)<0 при 0<x<1 и x>e. Так что f(x) – возрастает при 1≤x≤e и
f(x) –убывает при 0<x≤1 и x≥e.
C–25
1. y=x
x
;
ln ln
x
x
xx
ye e==; y'=(e
xlnx
)'=e
xlnx
⋅(xlnx)'=e
xlnx
(lnx+1)=x
x
(1+lnx).
2.
5
4
16,08 32,60 0,005−≈−.
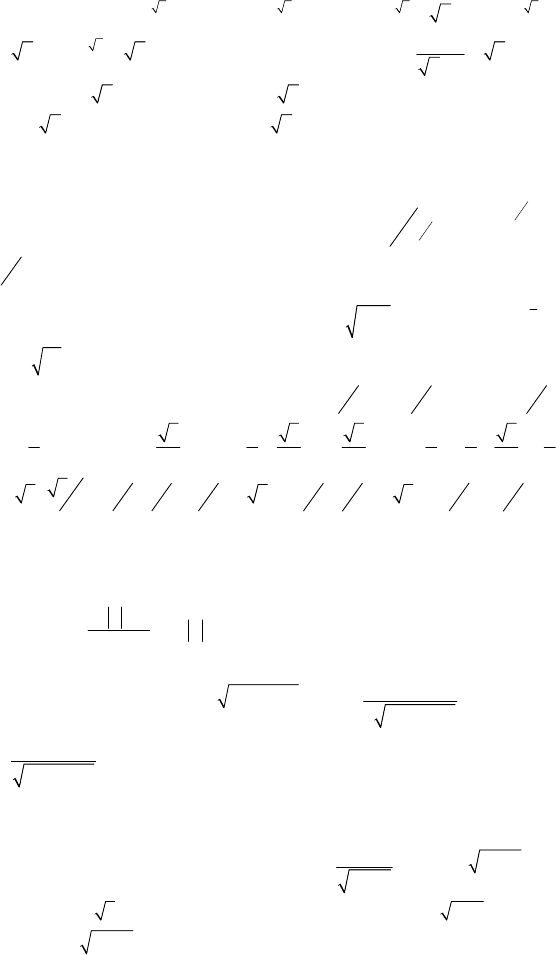
72
3.
2222
=( 2 +1) +( 2 +1)( )yxx xxxx
′′
′
−⋅ − =
2221
2( 1) 2 ( 1)xx x x
−
−
⋅+ −⋅ =
=
21
2( 1) ( 2 1)xx xx
−
−+−; y'=0 при x=0, x=1 и
1
21.
21
x
=
=−
+
y'>0
при
021x<< −
и x>1, y'<0 при
21 1x
−
<<
. Так что y – возрастает
на
[0; 2 1] [1; )−∪ ∞и убывает на 21;1
⎡
⎤
−
⎣
⎦
.
С–26
1. Каждый раз, через 3 часа – остается половина вещества. Значит до-
пустим, через t часов останется 0,25 кг. Тогда
3
8
0, 25
2
t
=
;
3
232;
t
=
5;
3
t
= t=15 (ч).
2. 3y
2
y'=y
3
; (y
3
)'=y
3
, так что y
3
=Ce
x
и
3
1
x
yCe= , то есть
3
x
yCe=
(где
3
1
CC= ).
3. y''=–0,25y; общее решение
cos sin ;
22
x
x
ya b
=+т.к.
()
3
0,
2
y = то
3
,
2
a
=
т.к.
()
3
'0
4
y = , то
3
,
24
b
=
3
2
b = ,
33
cos sin
222 2
x
x
y
=
+=
(
)
3
1
3cos sin 3cos
2222 26
xx x
⎛⎞
π
=+=−=
⎜⎟
⎝⎠
(
)
11
3cos
26
x
π
+ .
Вариант 10
С–1
1. При x>0 F'(x)=(x
4
)'=4x
3
=f(x); при x<0 F'(x)=(–x
4
)'=(–4x
3
)=f(x) При x=0:
() ()
3
2
0
0
0lim
x
xx
Fxxfx
x
→
−
′
===
. Так что при всех F'(x)=f(x), что и
требовалось доказать.
2.a) Является, т.к.
()
52/
'(437)Fx x x=−+
()
/
52
52
1
43
24 3
xx
xx
=
⋅− =
−
=
()
4
52
10 3
43
xx
f
x
xx
−
=
−
при всех x∈(1;2);
б) Нет, так как F(x) и f(x) определены не для всех x∈(–2;–1).
C–2
1. Общий вид первообразной для
()
2
1
x
fx
x
=
+
:
()
2
1Fx x C
=
++ , а
так как
(3;3)M принадлежит графику F(x), то 331,C
=
++ С=1 и
()
2
11Fx x=+ +
.
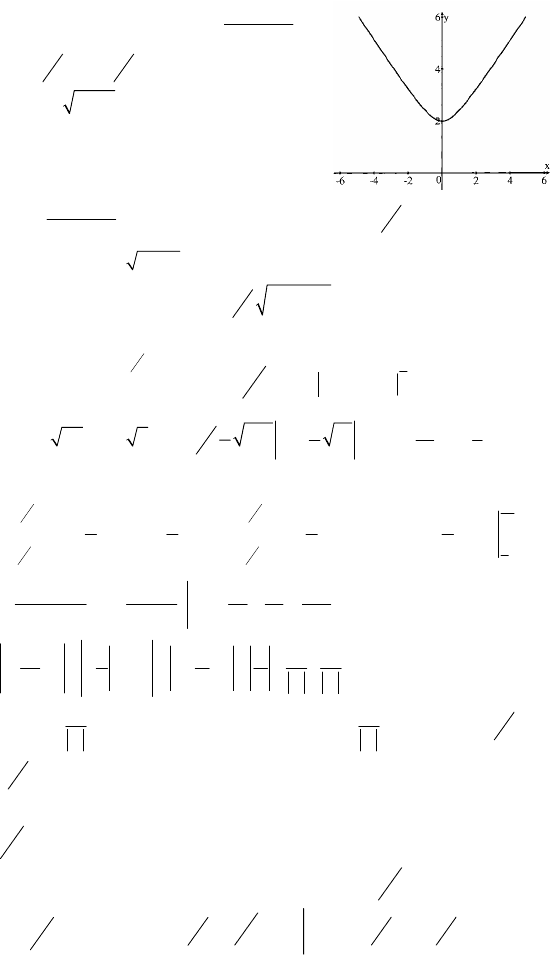
73
2. a) Так как
()
2
1cos2
sin ,
2
x
fx x
−
== то
()
sin 2
;
24
xx
Fx C=− +
б)
()
3
1.Fx x C=++
С–3
a)
2
2
()= +3cos(3 4)+1
sin ( +1)
f
xx
x
−
,
3
() 2tg( 1) sin(3 4)
4
F
xx xxC
=
+− − ++
;
б)
(
)
cos 1 2
g
xx x x=−+; так как (xsinx)'=sinx+xcosx, то (xsinx+cosx)'=
= xcosx и
() ()
3
1
sin cos 1 2 .
3
Fx x x x x C=+− ++
C–4
a)
() ()
0
2
2
0
2
0
2
20
2 2cos ( )2 2sin 242
2
x
Sxdx xdx x x
π
π
−
−
=+ + = + + =−++=
∫∫
4;
б)
04
04
33
90
90
22 161
2
18 23 .
3
33 33
Sxdxxdx x x
−
−
=−+ =− − + =+=
∫∫
С–5
1.а)
33
88
88
12sin cos = 6sin 2 =
88 4
x
xdx xdx
ππ
ππ
ππ π
⎛⎞⎛⎞ ⎛ ⎞
−− −
⎜⎟⎜⎟ ⎜ ⎟
⎝⎠⎝⎠ ⎝ ⎠
∫∫
3
8
8
3cos 2
4
x
π
π
π
⎛⎞
−
⎜⎟
⎝⎠
=–3;
б)
3
2
3
32 3
2
2
611138
53 15 795
(2 1) 2 1
xdx
xx
⎛⎞
=− =− + =
⎜⎟
−−
⎝⎠
∫
.
2.
1
1
2
1111
1= 1=1 1= =
A
A
dx
x
AAA
x
−
−
−
−
−− − −−
∫
;
1
0,1
A
<
при |A|>10, т.е. А>10
(т.к. А>1);
1
0,001
A
<
при |A|>1000, т.е. А>1000;
1
A
<
ε при |A| >
1
ε
, т.е.
А>
1
ε
.
C–6
1.
2
9
x
=х–2 при x
3
–2x
2
–9=0; т.е. (x
3
–27)–2(x
2
–9)=(x–3)(x
2
+3x+9–2x–6)=
=(x–3)(x
2
+x+3)=0 при x=3; и при 2<x<3
2
9
2x
x
>−
, так что
3
3
2
2
2
2
99
((2))( 2)
2
x
Sxdx х
х
x
=−−=−−+=
∫
99
36241.
22
−
−+++−=
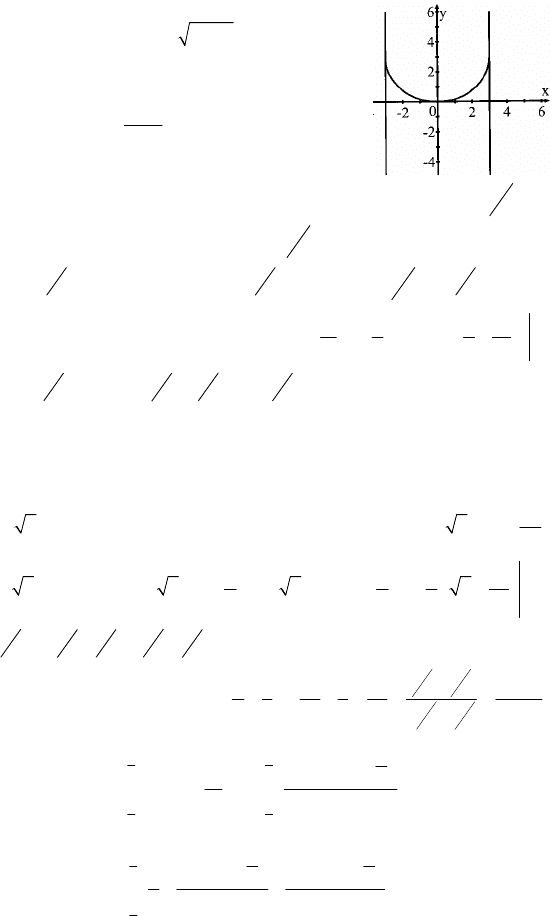
74
2. Интеграл равен площади фигуры, ограни-
ченной линиями
2
39yx=− − и x=3 и x=–3 и
y=0. Это прямоугольник со сторонами 3 и 6
без полукружности радиуса 3.
Так что
2
3
63 18 4,5
2
S
π⋅
=⋅− = − π
.
С–7
По формуле Ньютона F(t)=ma(t). Так что
() ()
3
4
:6at Ft m t
t
==−
. Да-
лее a'(t)=V(t), так что
()
2
2
2
3Vt t C
t
=
++, а так как V(2)=2, то
1
212 ,
2
C=+ +
так что
1
10 ;
2
C =−
()
2
2
21
310;
2
Vt t
t
=+ −
так как
S'(t)=V(t), то:
() () ()
88
2
2
33
21
83= =3 10=
2
SS Vtdtt dt
t
⎛⎞
−+−
⎜⎟
⎝⎠
∫∫
8
3
3
221
2
tt
t
⎛⎞
−−
⎜⎟
⎝⎠
=
63
12 11
512 84 27 432
43212
=−−−++ = (м).
С–8
1. Найдем точки пересечения y
4
+y
2
=2, y
2
=1, y=±1, x=±1. Площадь
внутри параболы равна площади сектора ограниченного y
2
+x
2
=2, y=x,
y=–x, x≥0 сложенный с площадью фигуры, ограниченной y=x и
yx= и с площадью фигуры ограниченной y=–x и yx=− .
1
2
4
S
π
=
+
+
()() ()
11 1
00 0
2
2
x
xdx x xdx x xdx
π
−+−+ =+ −=
∫∫ ∫
1
2
0
2
2
23 2
x
xx
⎛⎞
π
+
−=
⎜⎟
⎜⎟
⎝⎠
(
)
21 1
2
23223
ππ
=+ − =+
. Площадь вне параболы равна площади
круга без S
1
, то есть
2
131
2
23 2 3
S
ππ
⎛⎞
=
π− + = −
⎜⎟
⎝⎠
;
1
2
1
32
23
3
1
92
23
S
S
π
+
π
+
==
π
π
−
−
.
2.
2
22
4
33
1cos2
6
cos
12 2
x
x
dx dx
ππ
ππ
⎛⎞
π
⎛⎞
+−
⎜⎟
⎜⎟
π
⎛⎞
⎝⎠
⎜⎟
−
==
⎜⎟
⎜⎟
⎝⎠
⎜⎟
⎝⎠
∫∫
=
2
2
3
cos 2 cos 2
1
66
42 4
xx
dx
π
π
⎛⎞ππ
⎛⎞⎛⎞
−−
⎜⎟⎜⎟
⎜⎟
⎝⎠⎝⎠
⎜⎟
++
⎜⎟
⎜⎟
⎝⎠
∫
=
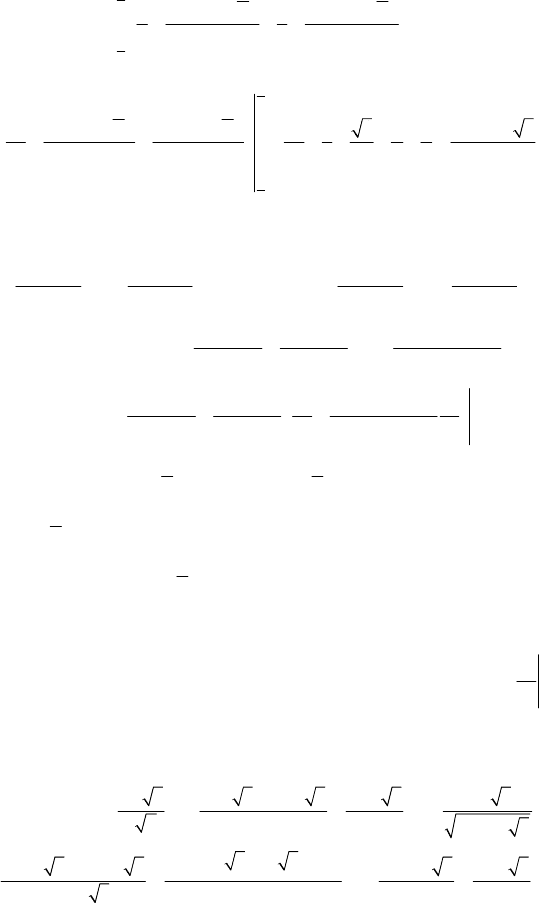
75
2
3
cos 2 cos 4
11
63
4288
xx
dx
π
π
⎛⎞
ππ
⎛⎞ ⎛⎞
−−
⎜⎟ ⎜⎟
⎜⎟
⎝⎠ ⎝⎠
⎜⎟
=+ ++ =
⎜⎟
⎜⎟
⎝⎠
∫
=
2
3
sin2 sin4
3
63
84 32
xx
x
π
π
⎛⎞ππ
⎛⎞⎛⎞
−−
⎜⎟⎜⎟
⎜⎟
⎝⎠⎝⎠
⎜⎟
++
⎜⎟
⎜⎟
⎝⎠
=
31 3 1
16 8 64 8 4
ππ
+
−−−=
48 3
64
π− −
.
С–9
1. Поперечное сечение многогранника – прямоугольник со сторонами
(
)
A
ax
A
h
−
−
и
(
)
B
bx
B
h
−
−
. Т.о.
()
(
)
(
)
A
ax B bx
Sx A B
hh
⎛−⎞⎛−⎞
=− −
⎜⎟⎜⎟
⎝⎠⎝⎠
.
()
()
() ()()
2
2
00
hh
AaB BbA AaBb
VSxdx ABx x dx
hh
h
⎛⎞
⎛− − ⎞ − −
==− + + =
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
∫∫
=
()() ()()
23
2
0
23
h
BAa ABb AaBb
xx
ABx
hh
h
⎛⎞
⎛− −⎞ − −
−+ + =
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
()()
()
()()
23
hh
A
Bh AaBb AaBb=− − −+− −=
=
(633332222)
6
h
A
BABaBABAbABaBAbab−+−++−−+ =
=
()()
()
22
6
h
B
AAbAa+++
.
2. Площадь части сферы, заключенной между плоскостями, проведен-
ными на глубине x и x+∆x, равна S
x
=2πr∆x, давление на эту часть
P
x
≈xS
x
ρ
g≈2πr
ρ
gx∆x Так что
0
2
r
rgxdx
ρ
=πρ =
∫
0
2
r
rgxdx
π
ρ=
∫
2
0
2
2
r
x
rgπρ
=
3
rg=π ρ , где
ρ
– плотность воды, g –ускорение свободного падения.
С–10
1. Верно, т.к.
3
3
13 133933533
82 8
22
⎛⎞
+++++
==
⎜⎟
⎜⎟
⋅
⎝⎠
и
3
3
23
20 12 3
⎛⎞
+
⎜⎟
⎜⎟
+
⎝⎠
=
(
)
(
)
26 15 3 12 3 20
81231833
144 3 400
20 12 3
+−
+++
== =
⋅−
+
20 12 3 5 3 3
32 8
++
==
.
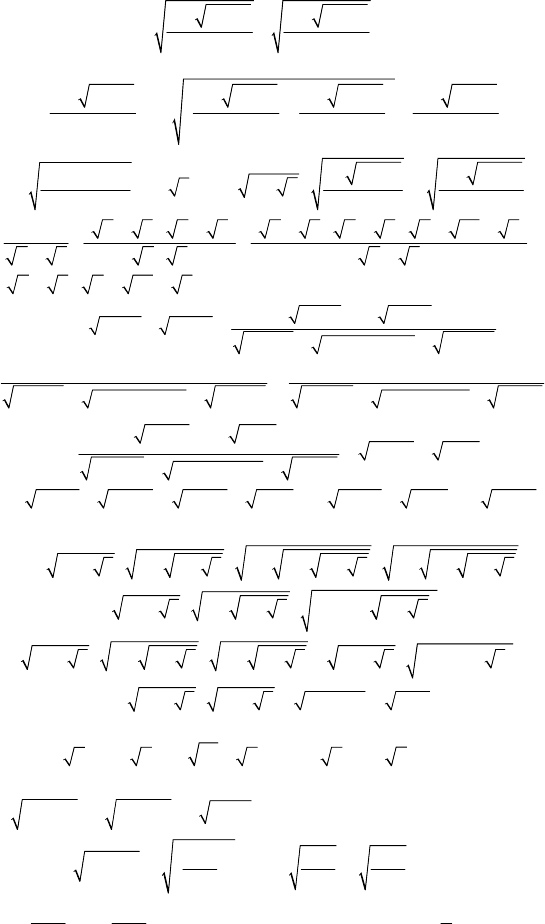
76
2.
2
22
22
aab aab
⎛⎞
+− −−
⎜⎟
−
=
⎜⎟
⎜⎟
⎝⎠
2222
2
2222
a ab a aba ab a ab
⎛⎞
⎛⎞⎛⎞
+− +− −− −−
⎜⎟
⎜⎟⎜⎟
=−⋅ +=
⎜⎟
⎜⎟⎜⎟
⎜⎟
⎝⎠⎝⎠
⎝⎠
=а–2
22
()
=
2
aab
ab
−−
−
. Т.о.
2
+
=
2
aab
ab
−
−
−
2
2
aab
−
−
.
3.
6633 3
66 66 66
()()()()( )
==
+
ab abab ababaabb
ab ab ab
−−+ −+−+
−+
=
=
36 3
()( )abaabb−++.
4.
33
33
33
33
22
3
( 10001) ( 10000)
10001 10000
10001 10001 10000 10000
−
−= =
+⋅+
=
33
22
3
1
10001 10001 10000 10001
<
+⋅+
33
22
3
1
10000 10000 9999 9999
=
+⋅+
()()
33
33
33
33
22
3
10000 9999
10000 9999
10000 10000 9999 9999
−
==−
+⋅+
.
Т.о.
33 3 3
10001 10000 10000 9999−<−, и
33
10001 9999
+
<
3
2 10000 .
С–11
1.
33863833383338+⋅++ ⋅+++ ⋅−++ =
(
)
33 8 6 3 8 9 3 3 8=+⋅++⋅−++=
()
33 8 6 3 8 6 3 8 33 8 36 3 8+⋅++⋅−+ = +⋅ −+ =
33 8 33 8 1089 8 1081=+⋅−= −= .
2.
a)
3
13 3xx+= +;
3
2
333
(1)( 1)3(1)xxx x
+
−+= +;
3
;
x
t
=
(t+1)(t
2
–t–2)=0;
t
1
=–1, t
2
=–1, t
3
=2; x
1
=–1, x
2
=8;
б)
() ()
22
3
2
33
12131
x
xx++ −=−x=1 – не является корнем, так что по-
делим на
()
2
3
1
x
−
.
2
3
3
11
23
11
x
x
x
x
+
+
⎛⎞
+=
⎜⎟
−
−
⎝⎠
;
3
1
;
1
x
t
x
+
=
−
t
2
–3t+2=0; t
1
=1,
t
2
=2;
1
1
1
x
x
+
=
−
и
1
8
1
x
x
+
=
−
; 1+x=1–x и 1+x=8–8x; x=0 и
7
9
x
=
.
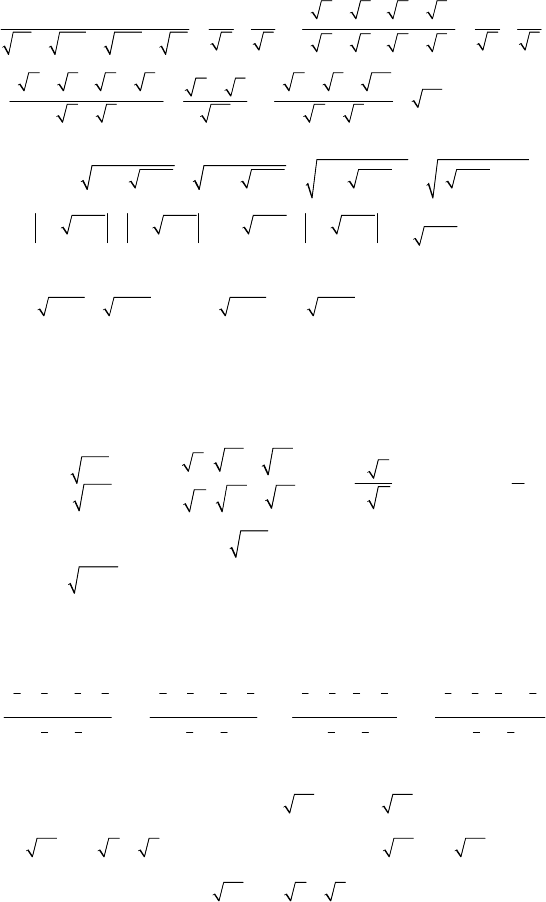
77
3. a)
(
)
(
)
()()
44 44
44
44 4 4
32 23
11 11
::
abab
ab
ab ab
abab
aababb
−+
−
⎛⎞ ⎛⎞
+= +
⎜⎟ ⎜⎟
−+
⎝⎠ ⎝⎠
−+−
=
(
)
(
)
(
)
4444 444
44
4
44 4 44
:
abab abab
ab
ab
ab ab ab
−+ +⋅
⎛⎞
+
===
⎜⎟
⎜⎟
−+
⎝⎠
, (при а>0, b>0,
a≠b);
б)
()()
22
21 211 1 11xx xx x x+ −+− −= +−+ −−=
{
2, 2,
11111111
21,1 2
x
xxxx
xx
>
=+ −+− −=+ −+− −=
−
≤≤
.
С–12
1.
33
974;xx−+ +=
3
9,
x
a
−
=
3
7,
x
b
+
= тогда
33
4,
;
16
ab
ab
+=
⎧
⎨
+=
⎩
22
4,
;
4
ab
aabb
+=
⎧
⎨
−+=
⎩
()()
2
2
4,
;
44 4
ab
bbbb
=−
⎧
⎨
−
−− +=
⎩
2
4,
;
312120
ab
bb
=−
⎧
⎨
−
+=
⎩
{
2,
;
2
a
b
=
=
{
98,
;
78
x
x
−=
+=
x=1.
2.
22
3
22
3
80,
;
5
xxxy
yyyx
⎧
⎪
+=
⎨
+=
⎪
⎩
(
)
()
3
22
3
3
3
22
3
3
80,
;
5
xx x y
yy y x
⎧
+=
⎪
⎨
+=
⎪
⎩
3
3
16
xx
yy
=
, то есть 8;
x
y
=±
x±8y; при x=8y:
23
3
64 8 8 80,yyy+=y
2
=1, y=±1,x=±8; при x=–8y:
22
3
64 8 8 80,yyy−−= y
2
=1, y±1, 8.x m То есть подходят решения: (8;1);
(–8;1); (–8;–1) и (8;–1).
С–13
1.
3
11 11
1111
33 33
2222
11 11
66 66
52 52 52 52
+
25 52
⎛⎞⎛⎞
⎜⎟⎜⎟
⋅+⋅ ⋅−⋅
⎜⎟⎜⎟
⎜⎟⎜⎟
+−
⎝⎠⎝⎠
=
33
111 1 111 1
3366 336 6
11 11
66 66
52(2+5) 52(5 2)
+
25 52
⎛⎞⎛ ⎞
⎜⎟⎜ ⎟
⋅⋅−
⎜⎟⎜ ⎟
⎜⎟⎜ ⎟
+−
⎝⎠⎝ ⎠
=10+10=20.
2.
()()
(
)
(
)
0,5 0,5
0,5 0,5
ax bx aba abb
−−
−−
++=+ +=
(
)
(
)
()()
(
)
(
)
0,5 1 0,5 0,5
0,5 0,5
ab a b a x x b a ab ab b
−− −−
−−
=+−−=−−=
(
)
(
)
0,5 1
ab a b
−
−
=−.
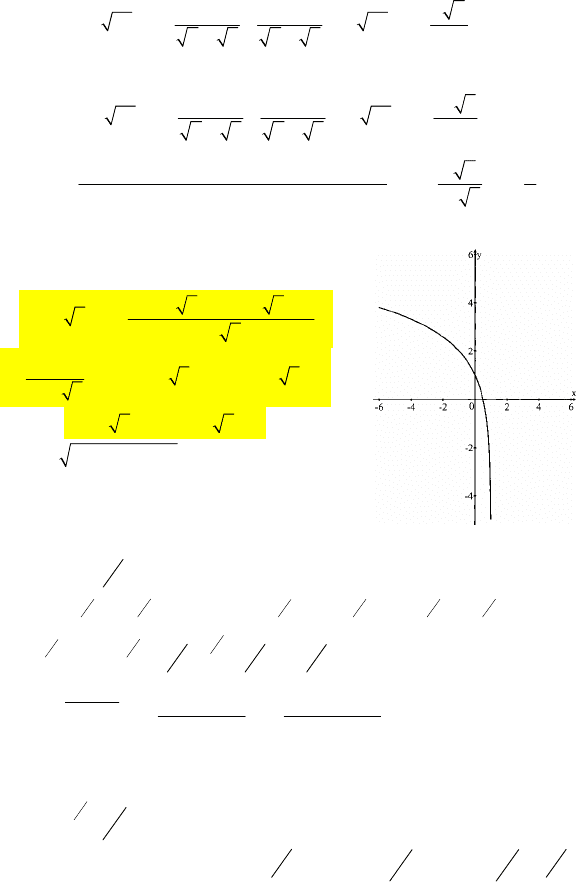
78
Так что
0,5 0,5 0,5 0,5
()() ()()ax bx ax xb
−− −−
+++−−=
() ()
0,5 0,5
11 2a
ab ab
ab
ab ab
−−
⎛⎞
⎛⎞
=+=
⎜⎟
⎜⎟
⎜⎟
−
+−
⎝⎠
⎝⎠
, и
0,5 0,5 0,5 0,5
()() ()()ax bx ax xb
−− −−
++−−−=
=
() ()
0,5 0,5
11 2b
ab ab
ab
ab ab
−−
⎛⎞
−
⎛⎞
−=
⎜⎟
⎜⎟
⎜⎟
−
+−
⎝⎠
⎝⎠
.
Так что
2
2
0,5 0,5 0,5 0,5
0,5 0,5 0,5 0,5
()() ()() 2
2
()() ()()
ax xb ax xb a b
a
b
ax xb ax xb
−
−
−− −−
−− −−
⎛⎞
⎛⎞
+++−−
=
=
⎜⎟
⎜⎟
⎜⎟
⎜⎟
−
++−−−
⎝⎠
⎝⎠
.
С–14
1.y=log
2
log
2
4
1–x
=log
2
((1–x)⋅log
2
4)=log
2
(2–2x)=
= 1+log
2
(1–x).
2.
()
3,3
3,3
3,3
((5 2 6) (5 2 6))
526
(5 2 6)
−++
−= =
+
()()
3,3
3,3 3,1
1
526 526
526
−−
⎛⎞
==+<+
⎜⎟
+
⎝⎠
.
То есть
3,3 3,1
(5 2 6) (5 2 6)
−
−<+ .
3.
22
33 20
xx
y
+
=−+; 3
2x
–3
x+2
+20≥0; 3
x
=t;
t
2
–9t+20≥0; t≤4 и t≥5; 3
x
≤4 и 3
x
≥5;
D(y)=(–∞; log
3
4]∪[log
3
5;∞), E(y)=[0;∞).
C–15
1. a)
(
)
2
1
1
1
3
3
x
x
+
+
=
;
2
11
33;
x
x
+
−−
= x
2
+1=–1–x; x
2
+x+2=0, решений нет;
б)
3
1
21
22
43 3 72 ;
xx
xx
++
−
−=−⋅
1111
2222
24 74 33 3 ;
xxxx−−++
⋅+⋅=⋅+
11
22
94 123 ;
xx−−
⋅=⋅
()
1
2
33
;
44
x−
=
1
1;
2
x
−
= x=1,5.
2. a)
2
310
3
8,6 1;
xx
x
+−
−
≤
2
310
0;
3
xx
x
+−
≤
−
(2)(5)
0;
(3)
xx
x
−+
≤
−
x∈(–∞;–5]∪[2;3);
б) x
2
⋅3
x
+9>x
2
+9⋅3
x
; (x
2
–9)(1–3
x
)<0; (x–3)(x+3)(1–3
x
)<0; x∈(–3;0)∪(3;∞).
C–16
1. a)
()
1
2
3
9 + +26 163+3
9
x
x
x
x
+
−
= ; 3(3
2x
+ 2 + 3
–2x
) + 20 = 16(3
x
+3
–x
);
3
x
+3
–x
=t; 3t
2
–16t+20=0; t
1
=2,
2
10
;
3
t =
3
x
=y;
1
2y
y
+
= и
10
1
;
3
y
y
+=
79
y
2
–2y+1=0 и 3y
2
–10y+3=0; y=1 и y=3 и
1
;
3
y =
3
x
=1, 3
x
=3 и
1
3;
3
x
= x
1
=0,
x
2
=1, x
3
=–1;
б)
( 7 48 ) ( 7 48 ) 14;
xx
++−= (7 48) ,
x
y
+
= тогда
()
( 7 48 ) ( 7 48 ) 49 48 1,
x
xx
+⋅−=−=так что
1
(7 48) ;
x
y
−=
1
14;y
y
+=
y
2
–14y+1=0;
1
748,y =+
2
748;y =− x
1
=2, x
2
=–2.
2.
ctg
tg
1
2;
2
x
x
−
⎛⎞
>
⎜⎟
⎝⎠
2
tgx
>2
ctgx
; tgx>ctgx; ctgx–tgx<0; 2ctg2x<0; ctg2x<0;
(
)
(
)
;;
42 4
x
nn kk
ππ π
∈+π +π∪−+ππ
, n, k∈Z.
C–17
1.
30
lg8 lg(1000 :125) 3 lg125 3 3
log 8
lg 30 lg(10 3) 1 lg 3 1
a
b
−−
== = =
⋅
++
.
2.
()
log
log log 1
0,5 2
2
3log
224
3
22 4
1
log 2 log log 2
2
x
x
x
xxx x
+
−
+⋅ + + =
=
()()
3
log
2
2
log
3
222 2
1
1 2log log log 1 2log 2
2
x
xxx x++ ++ + =
=
()
3
223
3
3
222 22 2
1 2log log log 2log log 1 log
x
xx xx x+ +++ +=+ =1+log
2
x.
3. 5
7
>3
10
, поэтому 5>
10
7
3 , так что
3
10
log 5
7
> ;
10
2
7
> , так как
100
2
99
> .
Так что
3
log 5 2> .
С–18
1.
ln 2 1yx=−−; y=1–lnx при 0
<
≤
x
e y=lnx–1
при
2
exe<≤ , y=3–lnx при
23
exe
<
≤ и y=lnx–3
при x>e
3
.
2. lgtg1°⋅lgtg2°⋅...⋅lgtg88°⋅lgtg89=0, так как
lgtg45°=lg1=0.
3.
2
lg 5lg 4yxx=++; lg
2
x+5lgx+4≥0; lgx=t;
t
2
+5t+4≥0; t≤–4 и t≥–1; lgx≤–4 и lgx≥–1; D(y)=(0;
10
–4
]∪[0,1; ∞).
С–19
1. а) log
x
(x+6);
{
2
2
60
0, 1,
0, 1,
0, 1;
2, 3,
60;
6
x
xx
xx
xx
xx
xx
xx
⎧
+>
>≠
⎪
⎧
>≠
>≠
⎨⎨
=
−=
−−=
⎩
⎪
+=
⎩
x=3;
80
б)
11
log 5 log 5; log 5 ;
22
xxx
x
yyy=− = + =− ;
2
2
0,
10,
10,
11 1
0; ; ;
1
1,
22 2
210
2
11
22
y
y
y
yy
yy
yy
yy
⎧
−≥
⎪
−≤ ≤
⎧
−≤ ≤
⎧
+≥ =−
⎨⎨⎨
==−
−−=
⎩
⎩
⎪
+=
⎩
.
2. а) lg(2x–1)+lg(2x–3)>lg(3x–3); lg((2x–1)(2x–3))>lg(3x–3);
2
210,
230,
48333;
x
x
xx x
⎧
−>
⎪
−>
⎨
⎪
−+>−
⎩
2
1
,
2
3
,
2
41160,
x
x
xx
⎧
>
⎪
⎪
>
⎨
⎪
−+>
⎪
⎩
()( )
{
1, 5,
24 3 0;
x
xx
>
−
−>
1, 5,
;2
3
2
4
x
x
xx
>
⎧
>
⎨
<>
⎩
б)
()()
10
29lg90
x
xx
−
−− −<; Область определения: х∈(9; 10], но при
таких x (x–9)lg(x–9)< 0, поэтому
()
10
2(9)lg90
x
xx
−
−
−−>, так что
решений нет.
С–20
1.а)
()
(
)
0,5lg 8 lg 1 5 ;xx−= + +
(
)
lg 8 lg 1 5xx
−
=++; 81 5;xx−=+ +
851;xx−− +=
()()
80,
50,
8285 51;
x
x
xxxx
⎧
−≥
⎪
+≥
⎨
⎪
−
−−+++=
⎩
()()
58,
;
85 6
x
xx
−≤ ≤
⎧
⎨
−+=
⎩
2
58
;
40 3 36
x
xx
−≤ ≤
⎧
⎨
+−=
⎩
1
2
2
1,
58,
340,
4.
x
x
xx
x
=
−
−≤ ≤
⎧
⎨
−−=
=
⎩
Но х=4 – посторонний корень, т.к.
84 4+5=11
−
−−≠
. Так что х=–1.
б)
11
99
1log 1 2log
x
x−+=−
.
1)
1
9
log 1x ≤
, т.е.
11
99
1
:1 log 1 2 log
9
x
xx≥− +=− – верно при всех
1
9
x ≥
;
2)
1
9
1log 2x<<
, то есть
11
99
11
: log 1 1 2 log ;
81 9
x
xx<< −+=⋅
1
9
1
log 1,
9
xx==
, не входит в
11
;
81 9
⎛⎞
⎜⎟
⎝⎠
;
