Сапожников А.А. Решение самостоятельных и контрольных работ по алгебре и началам анализа за 11 класс
Подождите немного. Документ загружается.

51
С–19
1. а) log
2x
64–log
2x
8=3;
2
64
log 3;
8
x
=
8=(2x)
3
; 8=8⋅x
3
; x
3
=1; x=1;
б) x
lgx
=100x; lgx
lgx
=lg100x; lg
2
x–lgx+2=0; lgx=2 и lgx=–1; x
1
=100, x
2
=0,1.
2. a) lg(x–1)
2
>0; (x–1)
2
>1; |x–1|>1; x<0 и x>2;
б)
()
21
2
1
log 1 log ;
23
x
x
⎛⎞
−>
⎜⎟
−
⎝⎠
log
2
(x–1)>log
2
(2x–3);
10,
230,;
12 3
x
x
xx
−>
⎧
⎪
−>
⎨
−
>−
⎪
⎩
1,
1, 5,
2
x
x
x
>
⎧
⎪
>
⎨
<
⎪
⎩
x∈(1,5;2)
C–20
1. a) lg
2
x
2
–3lgx
2
=4; lgx
2
=t; t
2
–3t–4=0; t
1
=4, t
2
=–1; lgx
2
=4 и lgx
2
=–1;
x
2
=10000 и
2
1
;
10
x = x=±100 и x=±
1
;
10
б)
4lg 3lg;
x
x−= lg ;
x
t
=
t
2
+3t–4=0; t
1
=1 и t
2
=–4; lg 1;x
=
lgx=1; x=10.
2. a)
()
(
)
2
11
22
log 2 3 log 6 ,xx−> −
2
2
230,
60, ;
23 6
x
x
xx
−>
⎧
⎪
−>
⎨
⎪
−
<−
⎩
2
2
1, 5,
6, ;
230
x
x
xx
>
⎧
⎪
>
⎨
⎪
−
−>
⎩
()()
6,
;
;1 3;
x
x
⎧
>
⎨
∈−∞− ∪ ∞
⎩
x ∈ (3;∞);
б) 4
x
–7⋅2
x
+12>0; 2
x
=t; t
2
–7t+12>0; 3<2
x
<4; log
2
3<x<2.
C–21
a)
()
33 3
3
log log 1 log 2
;
log 2
xy
xy
+=−
⎧
⎪
⎨
+=
⎪
⎩
()
33
33
log log 1, 5
;
log log 9
xy
xy
=
⎧
⎪
⎨
+=
⎪
⎩
{
1, 5
;
9
xy
xy
=
+
=
()
{
9,
;
29 3
xy
yy
=−
−⋅=
2
9,
;
21830
xy
yy
=−
⎧
⎨
−
+=
⎩
1
1
953
,
2
953
2
y
x
⎧
−
=
⎪
⎪
⎨
+
⎪
=
⎪
⎩
и
2
2
953
,
2
953
;
2
y
x
⎧
+
=
⎪
⎪
⎨
−
⎪
=
⎪
⎩
б)
()
2
3 2 576,
;
log 4
xy
yx
⎧
⋅=
⎪
⎨
−=
⎪
⎩
3 2 576,
;
4
xy
yx
⎧
⋅=
⎨
−=
⎩
426
32 32,
;
4
xx
yx
+
⎧
⋅=⋅
⎨
=+
⎩
{
2,
6.
x
y
=
=
С–22
1.а) f(x)=3–x
3
;
()
3
3
x
fx=− , так что
(
)
3
3
g
xx
=
− – обратная к f(x):
D(g)=E(g)=R;
б)
23
() (1 )fx x
−
=+ ,
0;x ≥
()
1
2
3
1;xfx
−
+=
()
2
2
3
1;xfx
−
+=
()
2
3
1,xfx
−
=− так что
()
3
2
1
1gx
x
=
− – обратная к f(x).
D(g)=E(f)=(0;1], E(g)=D(f)=[0;∞).
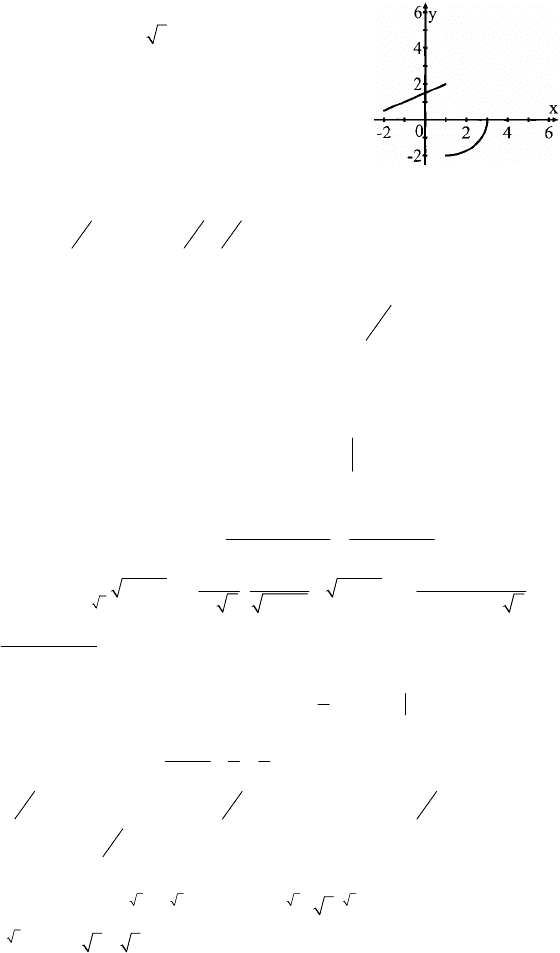
52
2. f(g(–1))=–1, f(g(1))=1, f(g(2)), так что g(–
1)=1, g(1)=2, g(2)=
3− ; D(g)=E(f)=[–2;3],
E(g)=D(f)=(–2;0]∪[0,5;2].
С–23
1.а) f'(x)=(e
2–14x
)'=e
2–14x
⋅(2–14x)'=–14e
2–14x
;
б)
()
(
)
() ()
/
0,5 1
0,5 1 0,5 1
111
() ln () 0,5 1'0,5ln0,50,5 .
222
x
xx
fx x
+
++
==⋅⋅+=⋅
2. Уравнение касательной к f(x) в точке x
0
: f(x)–f(x
0
)=f'(x
0
)(x–x
0
), так как
эта прямая параллельна y=2x+1, то f'(x
0
)=2, то есть
00
/
()2;
xx
ee
−
−=
00
/
()2
xx
ee
−
+=, то есть
0
0
1
2;
x
x
e
e
+
=
0
1
x
e
=
и
0
0x = .
Далее, f(x
0
)=e
0
–e
0
=0 и искомое уравенение y=2x.
3.
()
33
3/ 2 3
'()(33),
x
xxx
fx e x e
−−
==−f'(x)=0 при х=±1. f'(x)>0 при x<–1 и
х>1, a f'(x)<0 при –1<x<1. Так что x
min
=1, x
max
=–1.
()
(
)
()( )
22
2
22
0
00
2222224226.
xx x x
Se edx e dxex e e=−− = − =− =−−=−
∫∫
C–24
1.a)
()
32/ 2
32/
32 32
(21) 34
'(ln(21)) ;
21 21
x
xxx
fx x x
xx xx
−+ −
=−+= =
−
+−+
б)
()
//
33
3
2
11
'(log32) (32)
ln 2 3 2
fx x x
x
=−=⋅⋅−=
−
()
2
33 2 ln 2
x
−
−
=
()
4
32 3ln2
x
=
−
.
2. x
2
–8x+7=0 при х=1 и х=7. Так что
7
7
1
1
7
7ln 7ln7.
Sdx x
x
== =
∫
3. f'(x)=(ln
3
x)'–(3lnx)'=
()
2
2
3ln 3 3
lg 1
x
x
xxx
−
=−; f'(x)=0 при lnx±1; x=e и
1
x
e
= ;
()
'0fx>
при
1
0
x
e
<< и x>e и f'(x)<0 при
1
.
x
e
e
<
< Так что
x
min
=e и
max
1
.x
e
=
C–25
1.
()( ) () ()
/
33/ 3 31
'=2 +()2= +3 2=
f
xxxx xxx x
−
−⋅ − − −
=
31
(+23 3)
x
xx
−
−−.
53
f'(x)=0 при
23
.
31
x =
+
f'(x)>0 при
23
,
31
x <
+
f'(x)<0 при
23
,
31
x >
+
так
что f(x) – взрастает на [0;
23
31
+
] и f(x) – убывает на [
23
31
+
;∞).
2.
66
64,12 63,64 0,0025.−≈
3. Для f(x)=
22
x
x
−
+ – первообразная
()
21 1 2
.
211 2
xx
Fx C
+−
=
++
+−
C–26
1. Не удовлетворяет, так как
() ()
11
/
33
11
'() .
33
xx
f
xe e fx
−
==−=
2. Общее решение уравнения f'(x)= ln5f(x) : f(x)=C⋅5
x
, а так как f(6)=5,
то 5=C⋅5
6
, C=5
–5
и f(x)=5
x–5
– искомое решение.
3. Общее решение
(
)
(
)
cos 3 sin 3 .ya x b x=+Так как y(0)=2, то a=2, а
так как y'(0)=6, то
36,b
=
23.b =
Так что
(
)
=2cos 3 +yx
3
1
23sin 3=4 cos 3+ sin 3
22
x
xx
⎛⎞
⎜⎟
⎝⎠
=
=
()
4cos 3
3
x
π
−=
(
)
5
4cos 3 .
3
x
π
−
A=4, ω= 3, ϕ=
5
.
3
π
Вариант 8
С–1
1. Является, так как
()
()
()
/
1
'21
1
Fx x fx
x
=+= =
+
на (–1;∞).
б) Нет, т.к.
() ()
/
43 3
11
'4 42
2
Fx x x fx x x
xxx
⎛⎞
=− =+ ≠ =−
⎜⎟
⎝⎠
на (0;∞).
2. a)
()
()
(
)
()
/
/
/
22 2
1
' 2sin cos sin 2 sin 2 sin 2
2
Fx x x x x x===⋅=2sin2xcos2x=
=sin4x=f(x) на (–3;0). Так что F(x) – первообразная для f(x) на (–3;0);
б) F'(x)=((x+2)
4
)'=4(x+2)
3
⋅(x+2)'=4(x+2)
3
=4x
3
+24x
2
+48x+32=f(x) на
(–∞;∞). Так что F(x) – первообразная для f(x) на (–∞;∞).
C–2
1. Общий вид первообразной для
h(x)=cosx : H(x)=sinx+C, а так как
()1,
6
H
π
−=то
1
1
2
C−+=
и С=1,5 и
H(x)=sinx+1,5.
54
2.
()
()
(
)
38 8 12
38
281,
814
812
xx
x
fx x
x
x
−+−
−
== =−+
+−
++
так что
() ()
1
28181.
12
Fx x x x C=− + ++
б)
()
11
cos cos cos sin cos cos sin cos sin
2442 224
xxx xx
f
xx x xx====
1
sin 2
8
x
.
Так что
()
1
cos 2 .
16
Fx x C=− +
C–3
a)
() ()
22
sin 1 1,5 ( 1) 1 ;
33
Fx x x x C=− − + + + +
б)
() ()
2
2
ctg 2 .
56
x
Fx x C=−−+
С–4
a)
()
5
2
23
25
2
02
0
2
55
243
xxx
Sdx xdx x
⎛⎞
=+− =+− =
⎜⎟
⎜⎟
⎝⎠
∫∫
55 8
155 10
33
+
−−+=
=
10 5 19
;
3
−
б)
5
5
6
6
2
2
11
cos sin 1 .
22
Sxdxx
π
π
π
π
=− =− =− + =
∫
С–5
a)
4
4
1
1
612
612 6;dx
xx x
=− =− + =
∫
б)
3
3
2
4
4
1
ctg 1;
3
sin
dx
x
x
π
π
π
π
=
−=−+
∫
в)
33
3
2
00
0
1cos2 sin2 3
sin .
22468
xx x
xdx dx
ππ
π
−π
⎛⎞
==−=−
⎜⎟
⎝⎠
∫∫
С–6
а)
()
1
23
1
2
1
1
2
2
2
12
23
xx
Sx xdx x
−
⎛⎞
=++ = +− =
⎜⎟
⎜⎟
⎝⎠
∫
121121
11;
2 38224 8
+− − + − =
б)
()
6
6
0
0
sin 2 3 3 3 3
cos 2 sin cos 1 1.
2424
x
Sxxdx x
π
π
⎛⎞
=−=+=+−=−
⎜⎟
⎝⎠
∫
55
С–7
Пусть S(t) – уравнение координаты точки. Тогда S'(t)=V(t), так что
()
32
,
32
tt
St t C=−++
а так как S(0)=–1, то С=–1 и
()
32
1,
32
tt
St t=−+−a(t)=S''(t)=2t–1.
C–8
1.
() ()
016
201
222sin
6
x
Sxdxxdx dx
−
π
=
++−+ =
∫∫∫
01
22
20
22
22
xx
xx
−
⎛⎞⎛⎞
=+ +−
⎜⎟⎜⎟
⎜⎟⎜⎟
⎝⎠⎝⎠
–
6
1
12
cos
6
xπ
⎛⎞
−=
⎜⎟
π
⎝⎠
11263
422
2
−+− + + =
ππ
12 6 3
3, 5 .
+
+
π
2.
(
)
8
8
2
2
3
3
2
2123222.
1
x
dx x
x
=+=⋅−⋅=
+
∫
C–9
1. Площадь сечения данного тела вращения S(z)=
π
(z
2
+4). Так что
()
()
3
3
33
2
33
3
44
3
z
VSzdz z dz z
−−
−
⎛⎞
==π+=+⋅π=
⎜⎟
⎜⎟
⎝⎠
∫∫
(9+12+9+12)π=42π.
2. Как и в варианте 7:
(
)
(
)
c
ch
abxch
p g bx dx
h
−
⎛−−+⎞
=
+=
⎜⎟
⎝⎠
∫
()
12
12
32
6
6
46
2
8 6 312 . ( ).
69
xx
g
xdxgxxgH
⎛−−⎞
⎛⎞
=+ =−+=
⎜⎟
⎜⎟
⎝⎠
⎝⎠
∫
C–10
1. Верно, т.к.
7430−>и
(
)
2
743 49563163
−
>− +⋅=97 56 3− .
2. а)
15 2
6
77
52 0
67
42
55 5 5 5 5 5 1;
−
−
⋅=⋅⋅==
б)
3
3
3
1 1 5 1 5 1 126 5 1
5:5 : 4.
565
55 5 55
5
⎛⎞
⎛⎞
++
++= =⋅=
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
3. а)
3
27,31 3,0114;≈ б)
3
4
7 7 3,5395.+≈
4.
()
3
1
1
7
14 42
42
13 13 13 2197 ,=== а
1
1
3
6
42
2 2 128 ,== так что
7
13 >
3
2 .
C–11
1.
56
56
bb≤ равносильно b≤|b| и верно при всех b.
56
2. a)
44
12
1;
13
xx
+=
++
4
2;
x
t
+
=
12
1;
11
tt
+
=
−+
2
12 2
1;
1
tt
t
++ −
=
−
t
2
–3t=0; t=0 и t=3;
4
2x
=
− и
4
1;x
=
x=1.
б)
36
318;xx==
6
;
x
t
=
t
2
+3t–18=0; t
1
=–6; t
2
=3;
6
6x
=
− и
6
3x = ;
x=3
6
=729.
3. a)
()()
22
322 322 12 12 1212−++=− ++ =−++=
211 2 22;=−++=
б)
() ()
22
4.ab ab ab ab+− = −=−
С–12
1.
2
12 35;xxx−= − −
()
2
2
12 35,
;
10
xxx
x
⎧
−= −−
⎨
−>
⎩
2
1,
;
60
x
xx
>
⎧
⎨
−
−=
⎩
{
1,
2 и 3.
x
xx
>
=
−=
2.
3
3
3
;
9
xy
xy
⎧
+=
⎨
+=
⎩
3
3
;
x
a
yb
⎧
=
⎨
=
⎩
()
()
22
3
;
9
ab
aba abb
+=
⎧
⎪
⎨
+−+=
⎪
⎩
22
3
;
3
ab
aabb
+=
⎧
⎨
−
+=
⎩
22
3
(3 ) (3 ) 3
ab
bbbb
=−
⎧
⎨
−
−−+=
⎩
;
2
3,
;
320
ab
bb
=−
⎧
⎨
−+=
⎩
1
1
1,
2
a
b
=
⎧
⎨
=
⎩
и
2
2
2,
;
1
a
b
=
⎧
⎨
=
⎩
1
1
1,
8
x
y
=
⎧
⎨
=
⎩
и
2
2
8,
.
1
x
y
=
⎧
⎨
=
⎩
C–13
1. a)
2
14 3 2148
113
3,5 3,5 3,5
33 8 3333
444
12 ·18 ·6 3 ·9 2 ·3 ·2 ·3 ·2 ·3 3 ·3
− − −−−−
⎛⎞⎛ ⎞
⎜⎟⎜ ⎟
−
=−=
⎜⎟⎜ ⎟
⎝⎠⎝ ⎠
(
)
(
)
2
1,5 0,5 1 3 1 1 3
2·3 3 2·3 3 32 1 21;=−=−=−=
б)
()()
3 1 2 105
1
11
32
33
5 15 7 105
21
57
··· 3aa aa aaaa a a====при а=3.
2. а)
1
7
7
()aa=− верно только при а=0;
б)
()
1
6
6
aa= равносильно |a|=a и верно при а≥0.
3.
()()
11 11
22 22
11 11
22 22
2
xy xy
xy xy xy
xy
xy x y xy x y
xy x y xy x y
⎛⎞
⎛⎞
⎜⎟
−+
−+−
⎜⎟
+⋅= + ⋅
⎜⎟
⎜⎟
+−
⎜⎟
⎝⎠
−−
⎝⎠
57
()()()()
()()
()()
22
22
xyxy xy xy xyxy
xy xy
xy x y x y
−+ −++ −+
⋅= ⋅=
⋅+ −
22
.
2
x
yxy
x
yxy
++
==
С–14
1. См. график.
2. а)
()
7
7
1
7,
7
−
= а
2,45 7
77,
−−
<
т.к. –
2,75<
7− , т.е.
()
7
2,75
1
7;
7
−
>
б)
() ()
5
55
2,5
555,
⎛⎞
==
⎜⎟
⎝⎠
так что
()
5
5
2,5
55.
⎛⎞
=
⎜⎟
⎝⎠
3.
1
3( );
3
x
y =− так как
1
() 0
3
x
> и y≥0, то 0≤y< 3, то есть E(y)=[0;3).
Далее
(
)
1
30;
3
x
−≥
()
1
3,
3
x
≤
x≥–1, то есть D(y)=[–1;∞).
C–15
1.a) 0,2
3–2x
+3⋅0,04
2–x
=8; 5⋅0,2
4–2x
+3⋅0,2
4–2x
=8; 0,2
4–2x
=1; 4–2x=0; x=2;
б)
63
4
21
3=27;
x
x
x
−
−
63
63
4
3=3;
x
x
x
−
−
6363
=;
4
xx
x
−
−
(6x–3)(x–4)=0;
1
1
2
x
=
и x
2
=4.
2. a)
()
1
1
2
3
2
1
27 ;
81
x
+
−
>
1
6
2
33;
x
+
>
1
62;
x
+
>
1
4;
x
>−
1
4
x <− и x>0;
б)
21 0,5
225 710;
x
xx++
+≥⋅2⋅2
2x
+5⋅5
2x
≥7⋅2
x
⋅5
x
;
(
)
(
)
2
22
257;
55
x
x
⋅ +≥⋅
(
)
2
;
5
x
t= 2t
2
–7t+5≥0; t≤1 и
5
;
2
t ≥
(
)
2
1
5
x
≤
и
(
)
5
2
;
52
x
≥ x≥0 и x≤–1.
C–16
1.a) 4⋅9
1,5x–1
–27
x–1
=33; 4⋅3
3x–2
–3
3x–3
=33; 12⋅3
3x–3
–3
3x–2
=33; 3
3x–3
=3; 3x–3=1;
4
;
3
x =
б)
22
sin cos
2+52=7;
xx
⋅
22
sin 1 sin
252 7;
xx−
+
⋅=
2
sin
2;
x
t
=
10
7;
t
t
+
= t
2
–7t+10=0;
t=2 и t=5;
2
sin
22
x
=
и
2
sin
25;
x
=
2
sin 1x
=
и
2
2
sin log 5;x = sinx=±1;
,.
2
xnn
π
=+π ∈Ζ
58
2.
2
215
4
7,3 1;
xx
x
+−
−
>
2
215
0;
4
xx
x
+−
>
−
(
)
(
)
35
0;
4
xx
x
−+
>
−
x∈(–5;3)∪(4;∞).
C–17
1.
7
21
8
3
55 55
3
4
0,04
7
log log 5 2 log log
8
()
bbb
ba b a
aa
−−
=⋅⋅=−+ −
.
2.
(
)
()
2
60 60 60 60 60
60
log 27 3 log 3 log 60 2log 2 log 5 3 1 2 .
25
ab=⋅ = − − = − −
⋅
3.а)
22
6
3
42 22 2
2
1546
log 54 log 9 2log 54 6log 9 log log
29
9
−= −⋅= = =
2
log 4 =2;
б)
33
log 11 log 2
3333
log 2 log 11 log 2 log 11 ,=⋅=
так что
33
log 11 log 2
2110.
−
=
С–18
1. а)
22
3
log 3 3 log 0,
22
−= >
так как
3
1,
22
>
а 21;>
б)
22 2 2 2 2 2
0, 27
log 3 log 0,09 log log 0,09 log 0, 27 log 0,09 log 0,09
0,09
+= +=−+=
2
log 0, 27 0,=<так как 2>1, a 0,27<1.
2. D(g):
20,
21,
30;
x
x
x
+>
⎧
⎪
+≠
⎨
−≥
⎪
⎩
2,
1,
3;
x
x
x
>−
⎧
⎪
≠
−
⎨
≤
⎪
⎩
D(g)=(–2;–1)∪(–1;3].
C–19
1. a) 3⋅2
x+1
–6⋅2
x–1
=12; 12⋅2
x–1
–6⋅2
x–1
=12; 2
x–1
=2; x–1=1; x=2;
б) x
lgx
=1000x
2
; lgx
lgx
=lg1000x
2
; lg
2
x=3+2lgx; lgx=t; t
2
–2t–3=0; t
1
=3, t
2
=–1;
lgx=3 и lgx=–1; x
1
=1000 и x
2
=0,1.
2. a)
411
9
28 ;
xx
+
<
3
41
3
22 ;
xx
+
<
3
41
;
3
xx
<+
11
;
3
x
<
x<0 и x>3;
б)
()
31
3
1
log 1 log ;
25
x
x
+<
+
() ( )
2
33
4
log 1 log 2 5
2
bb ac
xx
a
−± −
+< +
;
10,
250,
12 5;
x
x
xx
+>
⎧
⎪
+>
⎨
+< +
⎪
⎩
1,
2,5
4;
x
x
x
>−
⎧
⎪
>−
⎨
>−
⎪
⎩
x>–1.
C–20
1. a) lg
2
x
2
+lgx
2
=6; lgx
2
=t; t
2
+t–6=0; t
1
=–3 и t
2
=2; lgx
2
=–3 и lgx
2
=2;
x
2
=0,001 и x
2
=100; x=±
0,001
и x=±10;
б)
52lg 3lg;
x
x−= lg ;
x
t
=
2t
2
+3t–5=0; t
1
=1 t
2
=–
5
;
2
lg 1x
=
и
5
lg ;
2
x =−
lgx=1; x=10;
59
2. a) log
3
(x
2
+5)>log
3
(x+7);
2
70,
;
57
x
xx
+>
⎧
⎨
+>+
⎩
2
7,
;
20
x
xx
>−
⎧
⎨
−−>
⎩
{
7,
;
1 и 2
x
xx
>−
<
−>
x∈(–7;–1)∪(2;∞);
б) 9
x
–8⋅3
x
+15<0; 3
x
=t; t
2
–8t+15<0; 3<t<5; 3<3
x
<5; 1<x<log
3
5.
C–21
a)
22 2
0,5
log log 2 log 5,
;
log ( ) 0
xy
xy
+=+
⎧
⎪
⎨
−=
⎪
⎩
()
22
0,5
log log 20,
;
log 0
xy
xy
=
⎧
⎪
⎨
−=
⎪
⎩
{
20,
;
1
xy
xy
=
−
=
()
{
1,
;
120
xy
yy
=+
+=
2
1,
;
20 0
xy
yy
=+
⎧
⎨
+− =
⎩
1
1
5,
4
x
y
=
⎧
⎨
=
⎩
и
2
2
4,
5
x
y
=
−
⎧
⎨
=
−
⎩
– не подходит, так как x>0 и y>0;
так что x=5, y=4;
б)
()
3
3 2 972,
;
log 2
xy
xy
⎧
⋅=
⎪
⎨
−=
⎪
⎩
3 2 972,
;
3
xy
xy
⎧
⋅=
⎨
−=
⎩
352
32 32,
;
3
xx
yx
−
⎧
⋅=⋅
⎨
=−
⎩
{
5,
2.
x
y
=
=
С–22
1. a) f(x)=1–8x
3
;
()
3
1
1
2
x
fx=−
, так что
()
3
1
1
2
g
xx
=
−
– обратная к
f(x). D(g)=E(g)=R;
б)
()
(
)
3
2
2,0;fx x x
−
=+ ≤
()
1
2
3
2;xfx
−
+=
()
3
2
2,xfx
−
=
−−так что
()
3
2
1
2
gx
x
=
− – обратная к f(x).
1
() 0; ,
8
Dy
⎛⎞
=
⎜⎟
⎝⎠
E(y)=(–∞;0].
2. f(g(–2))=–2, f(g(–1))=–1, f(g(3))=3, так что
g(–2) не определено, g(–1)=1–
3; g(3)=–1,5.
D(g)=E(f)=[–3;–2,5]∪(–2;4],
E(g)=D(f)=[–2;1)∪[2;3].
C–23
1. a) f'(x)=(e
4–7x
)'=e
4–7x
(4–7x)'=–7e
4–7x
;
б)
f'(x)=(4
2–3x
)' =4
2–3x
⋅ln4⋅(2–3x)'=–3⋅4
2–3x
⋅ln4.
2. Уравнение касательной в точке
x
0
: f(x)–f(x
0
)=f'(x
0
)(x–x
0
), а так как ка-
сательная – горизонтальная, то
f'(x
0
)=0, то есть
0
()
xx
xx
ee
−
=
′
+
=
=
00
0,
xx
ee
−
−= так что x
0
=0 и f(x
0
)=e
0
+e
0
=2; и y=2 – искомое уравнение.
3.
()
42 42
23 2
' ( ) (4 4 )( ),
xx xx
fx e x xe
−−
==− f'(x)=0 при x=±1 и x=0, f'(x)>0
при
x∈(–1;0)∪(1;∞), f'(x)<0 при x∈ (–∞;–1) ∪ (0;1). Так что x
min
=±1,
x
max
=0.
60
4.
()
()
()
()
2
2
213 213
1
1
1
11
2
xx xx
S e ee edx e ee ex
++
=− ++ − =− ++ −⋅ =
∫
4
2
e
−
+
+
()
3
1ee+−
()
432
32 23
2
1
21 .
22
eee
eeeee
−−
+−++=
C–24
1. a)
()
()
()
()
43
32
43
43 43
3
491
'ln3 ;
33
xxx
xx
fx x x x
x
xx x xx
′
−+
′
−
−
=−+= =
−+ −+
б)
()
()
44
4
3
11
' log 40,1 40,1
ln 3 4 0,1
fx x x
x
′
=−=⋅ ⋅−=
−
()
111 1
0,1 2 .
4 ln3 4 0,1 2 80 ln3
xx
=− ⋅ ⋅ ⋅ ⋅ =
−−
2.
x
2
–6x+5=0 при x=1 и x=5. Так что
5
5
1
1
5
5ln 5ln5.
Sdx x
x
== =
∫
3.
()
423
222 2
11
' =(log ) (2log ) =4log 4log
ln 2 ln 2
fx x x x x
xx
′′
−⋅−⋅
=
2
2
2
4log
(log 1)
ln 2
x
x
x
−
, f'(x)=0 при x=1, x=2,
1
2
x =
. f'(x)>0 при x>2 и
1
1
2
x
<<, f'(x)<0 при
1
2
x < и 1<x<2. Т.о.
min
1
2
x = и x
min
=2, x
max
=1.
C–25
1.
22
()=( 1) +( 1)( )fx x x x x
′′
′
−−
=
221
2( 1)xxx
−
+− =
21
(22)xx x
−
+−
,
f'(x)=0 при
2
.
21
x =
+
f'(x)>0 при
2
21
x >
+
и f'(x)<0 при
2
21
x <
+
, так
что
f(x) убывает на [0;
2
21
+
] и возрастает на [
2
21
+
;∞).
2.
55
32,15 31,75 0,005.−≈
3.
()
31 1 3
311 3
xx
Fx C
+−
=++
+−
.
C–26
1. Нет, так как f'(x)=(e
–3x
)'=e
–3x
(–3x)'=–3e
–3x
=–3f(x).
2. Общее решение
f'(x)=ln9f(x) : f(x)=C⋅9
x
, а так как f(3)=9, то 9=C⋅9
3
и
С=9
–2
и f(x)=9
x–2
– искомое решение.
3. Общее решение
y''=–4y : y=acos2x+bsin2x. Так как y(0)=1, то a=1, а
так как
y'(0)=–2
3
, то b=–
3
и cos 2 3 sin 2 2cos(2 );
3
yx x x
π
=− = +
A=2; ω=2; ϕ=
3
π
.
