Сапожников А.А. Решение самостоятельных и контрольных работ по алгебре и началам анализа за 11 класс
Подождите немного. Документ загружается.

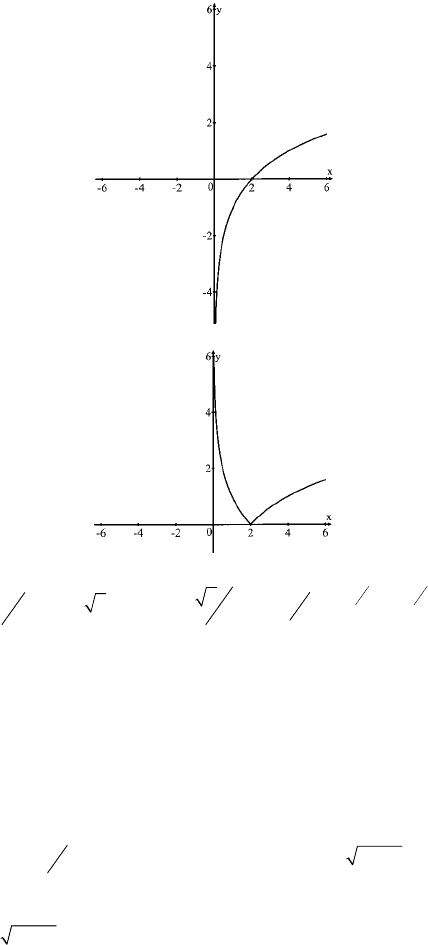
21
б) При x∈[0,5;8]: y
наим.
=0, у
наиб.
=2.
C–19
1. а)
2
44
1
log log 3
x
x
+=−;
2
44
1
log log
64
x
x
= ;
33
22
16x
−−
= ; x=16;
б) lg10x⋅lg0,1x=3; (1+lgx)(–1+lgx)=3; lg
2
x–1=3; lgx=±2; x
1
=100, x
2
=0,01.
2. a) lg2x<lg(x+1);
20,
10,
21
x
x
x
x
>
⎧
⎪
+>
⎨
<+
⎪
⎩
;
0,
1,
1
x
x
x
>
⎧
⎪
>−
⎨
<
⎪
⎩
; x∈(0;1);
б) lоg
2
(1–x)<1;
{
10,
12
x
x
−>
−<
;
{
1,
1
x
x
<
>−
; x∈(–1;1).
C–20
1. log
0,5
(2x–3)–
1
2
log
0,5
(2x+3)=0; log
0,5
(2x–3)=
0,5
log 2 3x
+
.
230,
230,
23 23
x
x
xx
⎧
−>
⎪
+>
⎨
⎪
−= +
⎩
;

22
2
1, 5,
1, 5,
412923
x
x
xx x
⎧
>
⎪
>−
⎨
⎪
−+=+
⎩
;
2
1, 5,
2730
x
xx
>
⎧
⎨
−
+=
⎩
;
1, 5,
;
1
3;
2
x
xx
>
⎧
⎨
==
⎩
x=3.
2. а) log
2
0,1
x≥1; log
0,1
x≤–1 и log
0,1
x≥1; x∈(0;0,1] ∪ [10;∞);
б)
(
)
2
3
log 2 4 0xx−−≤;
2
3
40,
log 2 0
x
x
⎧
−≥
⎨
−
≤
⎩
;
2
4,
09
x
x
⎧
≥
⎨
<
≤
⎩
;
x∈[2;9].
C–21
a)
33
log log 1,
29
xy
xy
−=
⎧
⎨
−=
⎩
;
0, 0,
3,
29
xy
x
y
xy
⎧
>>
⎪
=
⎨
⎪
−=
⎩
;
0, 0,
3,
329
xy
xy
yy
>>
⎧
⎪
=
⎨
−=
⎪
⎩
;
{
27
9
x
y
=
=
;
б)
(
)
3
1
log 1,
3224
xy
yx
+
⎧−=
⎨
⋅=
⎩
;
131
3,
3223
xy
yx
+
−=
⎧
⎨
⋅
=⋅
⎩
;
{
0,
3.
x
y
=
=
C–22
a) y=
1
3
−
x+2; y=6–3x– обратная.
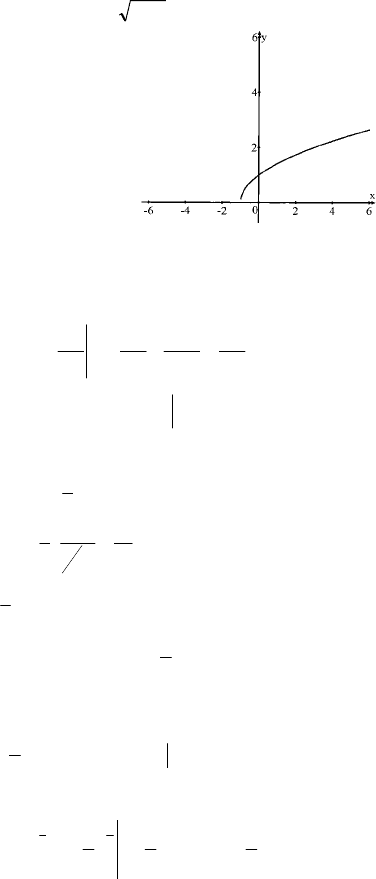
23
б) y=x
2
–1, x≥0; 1+= xy – обратная.
C–23
1. f(x)=e
–2x
cos3x;
f'(x)=–2e
–2x
cos3x–3sin3xe
–2x
;
f'(0)'= –2.
2.
3
3
1
1
327180
3.
ln3 ln3 3ln3 ln3
x
x
dx
−
−
==−=
∫
3.
()( )
2
2
22
0
0
12134,4.
xx
Se dxexe e=−=−=−−=−≈
∫
C–24
1. f(x)=10ln
1
5
x;
f'(x)=
11 10
10 ;
1
5
5
x
x
⋅⋅ =
5
'
3
f
⎛⎞
⎜⎟
⎝⎠
= 6.
2. ϕ(x) = lnx – x; ϕ'(x) =
1
1
x
−
; ϕ'(x) = 0 при x = 1, ϕ'(x) > 0 при 0 < x < 1,
ϕ'(x) < 0 при x > 1. Так что ϕ(x) – возрастает при 0 < x ≤ 1 и ϕ(x) –
убывает при x ≥ 1.
3.
()
4
4
1
1
4
1 4ln 4ln4 4 4ln1 1 4ln4 3 2,55
dx x x
x
⎛⎞
−= −=−−+=−≈
⎜⎟
⎝⎠
∫
.
C–25
1.
()
8
14
8
33
1
1
33 1
16 1 11
44 4
Sxdx x===−=
∫
.
2. Уравнение касательной:
y=f(x
0
)=f'(x
0
)(x– x
0
); f(x)=x
–2
, x
0
=–1, так что f(x
0
)=1; f'(x
0
)=–2(–1)
–3
=2;
y–1=2(x+1);искомое уравнение: y=2x+3.
24
C–26
1. y=3e
–4x
, y'=(3e
–4x
)'=3e
–4x
(–4x)'=–12e
–4x
=–4y, что и требовалось доказать.
2. y'=–2y. Общий вид решения: y=C⋅e
–2x
; так как y(0)=e, то e=c⋅e
–2⋅(0)
=C;
так что y=e
–2x+1
— искомое решение.
Вариант 4
С–1
1. а) F '(x)=
()
/
23
6
12
(3)
f
x
xx
−
−= = для всех x∈(–∞;0), так что F(x) –
первообразная для f(x) на промежутке (–∞;0).
б) F'(x)=
(
)
()
()
/
/
1,5 1 2
3
8
44
x
xx fx
x
−− −
⋅= =−= для всех х∈(0;∞), так что
F(x) – первообразная для f(x) на промежутке (0;∞).
2. а)
2
1
'( ) (3 3ctg ) ' 3
sin
Fx x x
x
=− =+ для всех x∈(0;π), так что F(x)
является первообразной для f(x) на (0;π).
б) Не является, так как
()
15
Fx
x
=
и
()
2
15
fx
x
=− определены не для
всех x∈(–4;4).
С–2
1. Первообразные для f(x)=х
–3
имеют вид
F(x)=–0,5x
–2
+С,
Две различные, например, F
1
(x)=–0,5x
–2
и
F
2
(x)=–0,5x
–2
+1.
2. Общий вид первообразной для
f(x)=cosx: F(x)=sinx+C, а так как точка
А(π;1) принадлежит графику F(x), то
1=sinπ+C, и С=1 и F(x)=sinx+1.
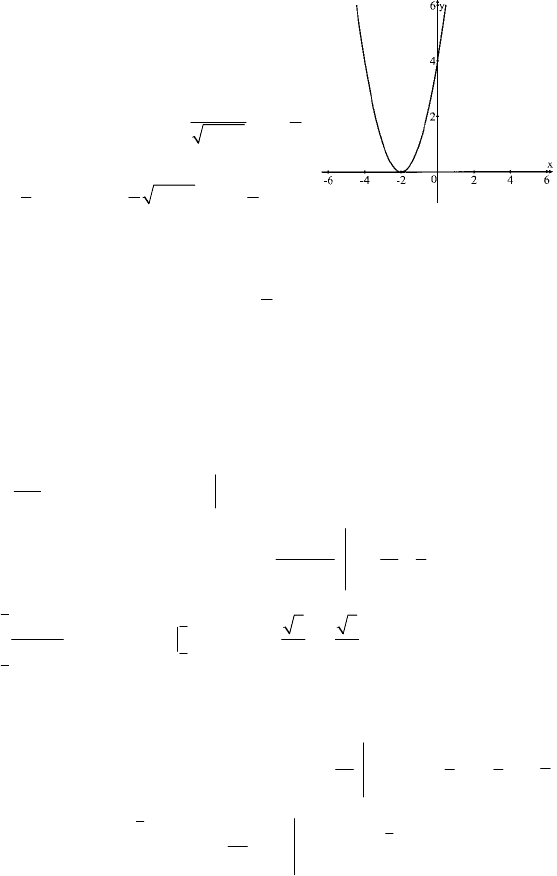
25
С–3
1. Общий вид первообразной для
f(x)=2x+4: F(x)=x
2
+4x+C, а так как
точка В(–1;1) принадлежит графику
F(x), то 1=(–1)
2
–4+С, то есть С=4 и
F(x)=x
2
+4x+4.
2. Для функции
()
1
cos
2
31
x
fx
x
=+
−
общий вид первообразных: при
()
12
;: 312sin
33 2
x
x
Fx x C
⎛⎞
∈∞ = −+ +
⎜⎟
⎝⎠
.
C–4
1. Заштрихованная фигура – трапеция с основаниями 1 и 0,5х+1 и
высотой x. Так что S(x)=
()
2
1
10,5 1 0,25
2
x
xx x++⋅=+
. Далее
S'(x)=(x+0,25x
2
)'=1+0,5x=f(x).
2. Площадь такой фигуры равна площади фигуры, ограниченной
линиями y=–2sinx, y=0, π≤x≤2π. Далее, F(x)=2cosx– является
первообразной для y(x)=–2sinx. По формуле S=F(b)–F(a) искомая
площадь S=2cos2π–2cosπ=4.
C–5
a)
()
99
9
0,5 0,5
1,5
1
11
4
48838116
x
dx x dx x
x
−
===⋅−⋅=
∫∫
;
б)
()
()
()
1
3
3
11
2
2
55
5
4
51
816 4 42;
333
x
xx dx x dx
−−
−
⎛⎞
+
⎜⎟
++ = + = =+=
⎜⎟
⎝⎠
∫∫
в)
()
4
4
2
6
6
833
4ctg2 4 0 4 4
33
sin 2
dx x
x
π
π
π
π
=− =−⋅ + ⋅ =
∫
.
C–6
а)
S=
1
3
11
22 2
11
1
(242)4(1)4
3
x
xxdx xdxx
−−
−
⎛⎞
−+− =⋅− =⋅−
⎜⎟
⎜⎟
⎝⎠
∫∫
=
11
41 1
33
⎛⎞
⋅−+−
⎜⎟
⎝⎠
=5
1
3
;
б)
() ()
0
2
0
2
2
0
20
2
22cos 2 2sin 2424.
2
x
S x dx dx x x
π
π
−
−
⎛⎞
=+ + =+ + =−++=
⎜⎟
⎜⎟
⎝⎠
∫∫

26
C–7
а) S=
0,5 1
2
+
⋅1=0,75;
б)
S≈S
10
=
11 111 121
...
210 2010 2010
⋅+⋅+⋅+
19 1
20 10
+
⋅=
()
1
10 11 12 ... 19
200
=++++=
(
)
10 19 10
0,725
2 200
+⋅
=
⋅
;
∆=|S–S
10
|=0,025;
в) S
n
=
11 11 21 2 21 2 11
...
22 2 2 2
nn n n
nnnnn nn nn
++ − −
⋅+ ⋅+ ⋅++ ⋅+ ⋅=
2
1
2
n
(n+(n+1)+
(n+2)+...+(2n–1))
(
)
2
21
11
0,75
24
2
nn n
n
n
+−⋅
=⋅ = −
; lim 0,75
n
n
S
→∞
=
.
C–8
а) S=
() ()
22
2
6
66
3
cos ( 2cos ) 3cos 3sin 3 4,5
2
xxdx xdxx
ππ
π
π
−
ππ
−−
−− = = = + =
∫∫
;
б) S=
()
1
1
3
22
3
3
12
32 3 31 99910 .
33 3
x
xxdxxx
−
−
⎛⎞
−+− = − − =−− ++−=
⎜⎟
⎝⎠
∫
C–9
1. a)
()
()
1
5
5
1
4
0
0
34
13
34 12,2
20 20 20
x
xdx
⎛⎞
−
⎜⎟
−= =+=
⎜⎟
−
⎝⎠
∫
;
б)
()
()
(
)
3
3
2
2
2
4
8ctg 8
24
sin
24
x
dx
x
π
π
π
π
π
=
−− =
π
−
∫
2. Площадь поперечного сечения равна S(x)=π⋅((x
2
+1)
2
–1)=π(x
4
+2x
2
).
Так что:
()
()
()
1
11
53
42
0
00
13
2
12
2.
53 53
15
xx
VSxdx x xdx
π
⎛⎞
= = π⋅ + =π⋅ + =π⋅ + =
⎜⎟
⎝⎠
∫∫
C–10
1. a)
6
6
(3 10) 10 3 10 10 10 3 10 2 10 3−+=−+=−+=−;
б)
56
56
2aaaaaaa−=−=+=, если а>0.
2. a) x
6
–1=0; x
6
=1; |x|=1; x±1; б) 27x
3
–1=0; x
3
=
1
27
; x=
1
3
.
C–11
1.
33
33
3
12 4 5 12 4 5 (12 4 5)(12 4 5) 144 80 64 4.+⋅−= + − = −==
27
2.
(
)
()()
()
2
2
2
55
5 5 25 10 5 5 30 10 5 3 5
25 5 2
55
5555
55
+
+++++
====
−
−
−+
−
.
3. x
6
<1; |x|<1, –1<x<1.
C–12
1.
2
3+6+1=7
x
xx− ;
()
2
2
2
70,
3+6+10,
3+6+1=7
x
xx
x
xx
⎧
−≥
⎪
≥
⎨
⎪
−
⎩
;
2
7,
66
(;1 ][1 ;),
33
+10 24 = 0
x
x
xx
≤
⎧
⎪
⎪
∈
−∞ − − ∪ − + ∞
⎨
⎪
−
⎪
⎩
66
1;7 ;1
33
12 и 2
x
xx
⎧
⎡⎤⎛ ⎤
⎪
∈−+ ∪−∞−−
⎜
⎢⎥ ⎥
⎜
⎨
⎢⎥ ⎥
⎣⎦⎝ ⎦
⎪
=− =
⎩
x
1
=2, x
2
= –12.
2.
4,
31
xy
xy xy
⎧
+=
⎨
+− =
⎩
;
,
x
a
yb
=
=
;
22
4,
31
ab
ab ab
+=
⎧
⎨
+
−=
⎩
;
() ()
2
2
4,
4341
ab
bb bb
=−
⎧
⎨
−
+− −⋅=
⎩
2
4,
430
ab
bb
=−
⎧
⎨
−+=
⎩
;
1
1
1,
3
a
b
=
⎧
⎨
=
⎩
;
2
2
3,
1
a
b
=
⎧
⎨
=
⎩
;
1
1
1,
9
x
y
=
⎧
⎨
=
⎩
и
2
2
9,
1
x
y
=
⎧
⎨
=
⎩
.
C–13
1.
5
5
5
32 2 2==;
6
3
6
82 2==
. Так что
5
6
32 8= .
2.3⋅0,0081
–0,25
+
(
)
0,75
1
16
−
=3⋅(0,3)
4⋅(–0,25)
+
()
(
)
3
4
4
2
−⋅−
=3⋅(0,3)
–1
+2
3
=10+8=18.
3.
1
22 22
3111
2222
()()
:
()
ab ab a ab abaa
bb
aa b
aab ab
−
⎛⎞
⎛⎞
−− −−−⋅
⎛⎞
⎜⎟
−= ⋅=
⎜⎟
⎜⎟
⎜⎟
⎜⎟
+
⎝⎠
⎜⎟
⎝⎠
++
⎝⎠
=
()
()
(
)
(
)
abab
ba b
a
ab
b
ab
aa b
−+
−
⋅= = −
+
+
.
C–14
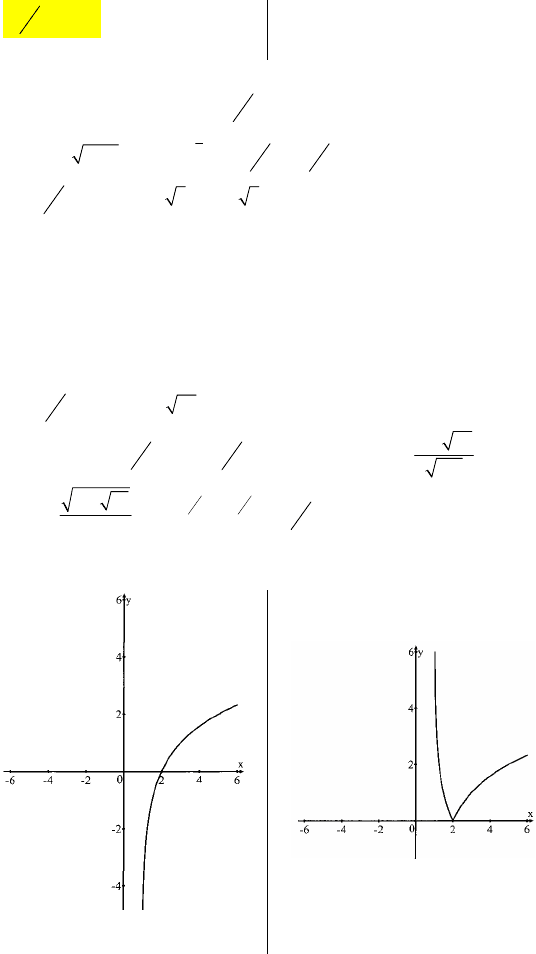
a)
б)
28
а)
2
2
3
y−<< при –1<x<1;
область значений y > –1;
б) при x∈[–2;2] y
наим
=0, а y
наиб.
=8.
C–15
1. а) 8
–х
=16; 2
–3х
=2
4
; –3x=4; x=
4
3
−
;
б) 10
2x
=0,1⋅ 1000 ; 10
2x
=
1
2
10 ; 2x=
1
2
; x=
1
4
.
2. a)
10,5
(tg ) 9
3
x−−
π
<
;
(
)
(
)
12
33
x
−
−
<
; x–1<–2; x<–1;
б)
2
0,5 3
927
x −
< ;
2
3
363
x
−< ;
2
63x
−
< ; x<9; |x|<3; –3<x<3.
C–16
1. 4
|x–1|
<8; 2
2|x–1|
<2
3
; 2|x–1|<3; |x–1|<1,5; –0,5<x<2,5.
2. а) 3
x+1
–4⋅3
x–2
=69; 27⋅3
x–2
–4⋅3
x–2
=69; 23⋅3
x–2
=69; 3
x–2
=3; x–2=1; x=3;
б) 4
x
–3⋅2
x
=40; 2
x
=t; t
2
–3t–40=0; t
1
=–5, t
2
=8; 2
x
=–5 и 2
x
=8; x=3.
C–17
1. 3lg5+
33
1
lg64 lg(5 64) lg1000 lg10 3
2
=⋅= = =
.
2.
77 7 7
11
log 2log 5 log 36 log 125
23
x =+ − ;
2
3
77
536
log log
125
x
⋅
=
; x=30.
3.
3
23
3
2
10 10
2
lg lg lg( 10 ) lg 1, 5
3
100
a
xa a
a
−
−
==⋅=−−
.
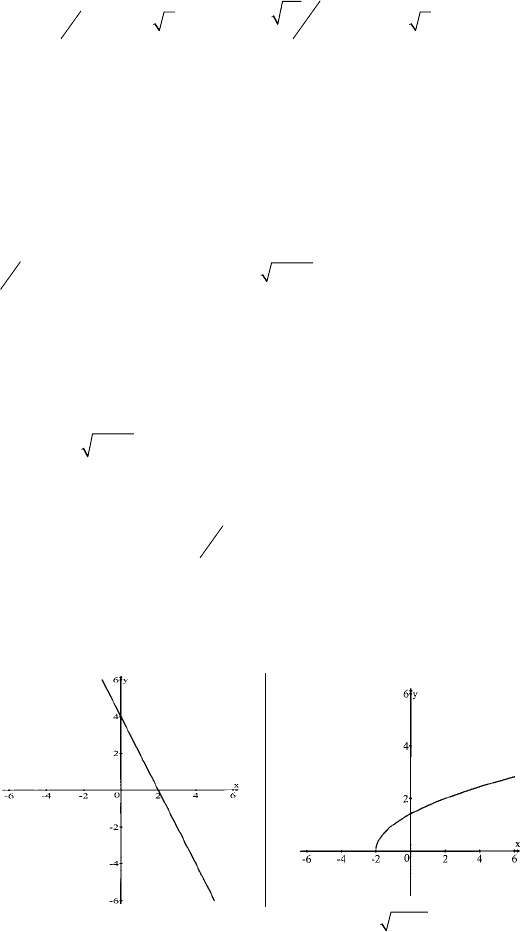
C–18
a) б)
–1<y<2 при 1,5<x<5;
при x∈[1,5; 9] y
наим
=0; y
наиб.
=3.
29
C–19
1. а)
3
0,5 0,5
1
log 4 log 1;x
x
+=−
3
4
0,5 0,5
log log 2
x
x
= ;
3
2x
=
; x=8;
б) lg100x⋅lg0,01x=5; (2+lgx)(lgx–2)=5; lg
2
x–4=5; lg
2
x=9; lgx=±3; x
1
=1000
и х
2
=0,001.
2. а) lg(3x)<lg(x+4);
30,
40,
34
x
x
xx
>
⎧
⎪
+
>
⎨
<
+
⎪
⎩
;
0,
4,
2
x
x
x
>
⎧
⎪
>−
⎨
<
⎪
⎩
; x∈(0;2);
б) log
0,5
(1–x)>–1; log
0,5
(1–x)>log
0,5
2;
{
10,
12
x
x
−
>
−
<
;
{
1,
1
x
x
<
>−
; x∈(–1;1).
C–20
1.
3
1
log
2
(5x–1)–
3
log (x+1)=0;
33
log 5 1 logx −= (x+1);
()
2
510,
10,
51 1
x
x
xx
⎧
−>
⎪
+>
⎨
⎪
−= +
⎩
;
2
0, 2,
1,
320
x
x
xx
⎧
>
⎪
>−
⎨
⎪
−+=
⎩
; x
1
=1, x
2
=2.
2. a) log
2
0,5
x≤1; –1≤log
0,5
x≤1; 0,5≤x≤2;
б)
2
2
(2 log ) 1 0xx−−≥;
2
2
0,
10,
2log 0
x
x
x
>
⎧
⎪
−≥
⎨
−
≥
⎪
⎩
;
2
2
0,
1,
log 2
x
x
x
>
⎧
⎪
≥
⎨
≤
⎪
⎩
;
0,
1
4
x
x
x
>
⎧
⎪
≤
−
⎨
≤
⎪
⎩
1,x ≥ x∈[1;4].
C–21
a)
44
log log 1,
316
xy
xy
−=
⎧
⎨
−=
⎩
;
4
log 1,
16 3
x
y
x
y
⎧
=
⎪
⎨
=+
⎪
⎩
;
4,
0, 0,
4163
xy
xy
yy
=
⎧
⎪
>>
⎨
=+
⎪
⎩
{
16,
64
y
x
=
=
;
б)
(
)
2
1
log 1,
23 72
xy
xy
+
⎧−=
⎨
⋅=
⎩
;
132
2
23 23
xy
xy
+
−=
⎧
⎨
⋅
=⋅
⎩
;
{
3,
1.
x
y
=
=
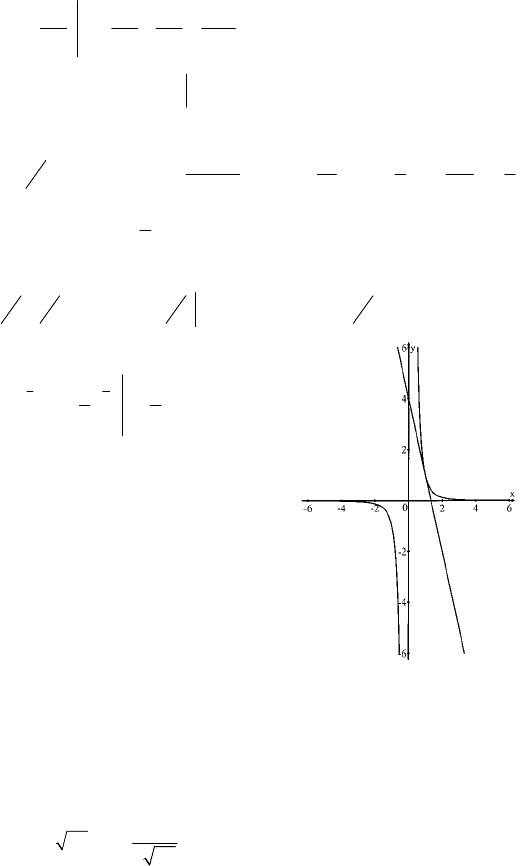
C–22
a) y= –0,5x+2; y=4–2x– обратная; б) y=x
2
–2; y= 2x
+
– обратная.
30
C–23
1. f(x)=e
–x
sin2x; f'(x)=–e
–x
sin2x+2cos2xe
–x
; f'(0)=2.
2.
2
2
1
1
5250,224,8
515,4
ln 5 ln 5 ln 5 ln 5
x
x
dx
−
−
⎛⎞
= =−= ≈
⎜⎟
⎜⎟
⎝⎠
∫
.
3.
()( )
0
0
22
2
2
1123
xx
Se dxex e e
−−
−
−
=−=−−=−+−=−
∫
.
C–24
1.
() ()
1
ln 4
8
f
xx=−;
()
()
()
/
11
'4
84 8
fx x
x
x
=⋅−=
−
,
341
'
4836
f
⎛⎞
−
=− =−
⎜⎟
⋅
⎝⎠
.
2. ϕ(x)=x–lnx; ϕ'(x)=
1
1
x
−
; ϕ'(x)=0 при x=1; ϕ'(x)>0 при x>1 и ϕ'(x)<0
при 0<x<1. Так что ϕ(x) – возрастает на [1;∞) и убывает на (0;1].
3.S=
()()
4
4
1
1
21 1
2ln 2ln4 2 2ln1 2ln4 1,5 1,27
22 2
x
dx x
x
−=−=−−+=−≈
∫
.
C–25
1.
()
8
14
8
33
1
1
33
216122,5
22
Sxdx x
⎛⎞
⎜⎟
== =⋅−=
⎜⎟
⎝⎠
∫
.
2. Уравнение касательной в точке x
0
:
y–f(x
0
)=f'(x
0
)(x–x
0
). Для f(x)=x
–3
: f'(x)=–3x
–4
и f'(1)=–3. Так что искомое уравнение:
y–1=–3(x–1) или y=–3x+4.
C–26
1. y'=(8e
–2x
)'=8⋅(–2)e
–2x
=–16e
–2x
=–2y, что и требовалось доказать.
2. y'=–4y. Общий вид решения: y=c⋅e
–4x
. А так как y(1)=e, то e=c⋅e
–4
и
с=e
5
, то есть y=e
–4x+5
– искомое решение.
Вариант 5
С–1
1. а) F '(x)=
()
()
/
1
2
x
fx
x
−=− =
−
для всех х∈(–∞;0), так что F(x) –
первообразная для f(x) на (–∞;0);
