Сапожников А.А. Решение самостоятельных и контрольных работ по алгебре и началам анализа за 11 класс
Подождите немного. Документ загружается.

41
2
0,
80,
80,
64
x
x
x
x
x
≥
⎧
+≥
⎪
⎨
−≥
⎪
−=
⎩
;
22
0,
8,
8,
64
x
x
x
x
x
≥
⎧
≥−
⎪
⎨
≤
⎪
−=
⎩
;
2
08,
32
x
x
≤
≤
⎧
⎨
=
⎩
;
{
08,
32
x
x
≤
≤
=±
; x= 42.
2.
6
6
3,
9
xy
xy
⎧
+=
⎨
+=
⎩
;
6
6
,
x
a
yb
⎧
=
⎨
=
⎩
;
()
()
22
3
9
ab
aba abb
+=
⎧
⎪
⎨
+−+=
⎪
⎩
;
22
3,
3
ab
aabb
=−
⎧
⎨
−
+=
⎩
;
()()
2
2
3,
33 3
ab
bbbb
=−
⎧
⎨
−
−− + =
⎩
;
2
3,
320
ab
bb
=−
⎧
⎨
−+=
⎩
;
1
1
1,
2
a
b
=
⎧
⎨
=
⎩
и
2
2
2,
1
a
b
=
⎧
⎨
=
⎩
;
1
1
1,
64
x
y
=
⎧
⎨
=
⎩
и
2
2
64,
1.
x
y
=
⎧
⎨
=
⎩
C–13
1.a)
(
2
3
3
2
1
8()
9
−
+
+
2
3
125 ))
1
2
=
3
(8)
2
+ (9)
3
+
6
2
( 125 )
1
2
=(4+27+5)
1
2
=
36
=6;
б)
11
11
33
22
12 19 : 12 19
−
⎛⎞⎛⎞
⎜⎟⎜⎟
−+
⎜⎟⎜⎟
⎝⎠⎝⎠
=
(
)
(
)
3
3
12 19 12 19 144 19
−
+=−
=
3
125 =5.
2.
()
()
5
5
2
10
4
3
34
12
93 3
−
⋅−
−
==, a
12
27
23
36
1
93 3
3
⎛⎞
−+−
−
−
⎜⎟
⎝⎠
⋅= =
, так что
()
5
2
4
3
3
1
99
3
−
−
>⋅, так как
10 7
12 6
−>−
и 3>1.
3.
21
3
2
3
33
81 81
4214 21
vv
vv vv
+−
−=
−+ ++
(
)
(
)
3
2
33
3
2
3
2+14 2+1
42+1
vvv
vv
−
−
−
–
(
)
(
)
3
2
33
33
3
2
3
214 2+1
=2 +1 2 +1=2.
4+2+1
vvv
vv
vv
−+
−
C–14
1. См. график.
2.a)
()
4
31
4
4
33231234
393 3
2
+
−++−
⋅= =
=3;
б)
22 2
111
(( ) ) ( ) .
224
==
3.
24
x
y =−; E(y)=[0;∞); D(y)=[2;∞), так как
2
x
–4≥0 при x≥2.
42
C–15
1. a) 3
x
+4⋅3
x+1
=13; 3
x
+12⋅3
x
=13; 3
x
=1; x=0;
б)
34
5
sin 8
6
x−
π
⎛⎞
=
⎜⎟
⎝⎠
;
3
34
2
1
2
2
x−
⎛⎞
=
⎜⎟
⎝⎠
;
3
34
2
11
22
x
−
−
⎛⎞ ⎛⎞
=
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
;
3
34
2
x
−
=−
;
5
6
x = .
2. a)
11
11
26
55
xx−+
⎛⎞ ⎛⎞
+≤
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
;
11
11
25 26
55
xx++
⎛⎞ ⎛⎞
+≤
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
;
1
1
1;
5
x+
⎛⎞
≤
⎜⎟
⎝⎠
x+1≥0; x≥–1;
б)
2
8
39
x
> ;
2
16
33
x
> ; x
2
>16; x∈(–∞;–4]∪[4;∞).
C–16
1. a)
2
2
27 811
x −
= ;
2
32
4
33
x −
=
;
2
4
2
3
x
−
=
;
2
10
3
x =
и
2
2
3
x
=
;
10
3
x =± и
2
3
x =± ;
б)
2
231
3
1
4
2
xx
x
+−
−
⎛⎞
=
⎜⎟
⎝⎠
;
2
231 62
11
;
22
x
xx+− −
⎛⎞ ⎛⎞
=
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
2x
2
+3x–1=6–2x; 2x
2
+5x–7=0;
x
1
=1, x
2
= –3,5.
2.
1
1
360
9
x
x−
⎛⎞
−+<
⎜⎟
⎝⎠
; 3
–2x
–3⋅3
–x
+6<0; 3
–x
=t; t
2
–3t+6<0; D<0, решений нет.
C–17
1. a)
33 333
3
log 18 log 4 2log 3 2 log 4 log 18 log 4−= −= −=
3
9
log
2
. Ве-
роятно в условиях опечатка, нужно:
3333 3
3
log 18 log 4 2log 18 log 4 log 324 log 4−= −= −=
33
324
log log 81
4
= =4;
б)
3
3
6
66 6
3
3
66
6
log 27 2log 2 log 27 2
=
11
log 0, 25 log
log 0, 25
3
3
⎛⎞
⎛⎞
+⋅
⎜⎟
⎜⎟
⎜⎟
⎜⎟
+
⎜⎟
⎜⎟
⎝⎠
⎝⎠
=
3
3
33
1
0,25
3
log 3 4
⎛⎞
⎜⎟
⋅
⎜⎟
⎜⎟
⎝⎠
=
3
34
log
−
=
=(3
3
4
3
)
3
. Вероятно в условиях опечатка, нужно:
3
62
66
log 27 2 log 2
1
log 0, 24 log
3
⎛⎞
+
⎜⎟
⎜⎟
⎜⎟
+
⎜⎟
⎝⎠
=
3
3
3
63
666
66
6
log 27 2 log 12 3log 12
11
log 12 log 12
log
43
⎛⎞
⎛⎞
⎛⎞
⋅
⎜⎟
⎜⎟
⎜⎟
==
⎜⎟
⎜⎟
⎜⎟
−−
⎜⎟
⋅
⎝⎠
⎝⎠
⎜⎟
⎝⎠
=(–3)
3
= –27.
2.
15 1
1
3
25
2
31
33 3
2
3
55
125
log log 5 3
3
abx
abx y z
yz
−
−
−
⎛⎞
⎜⎟
=
⋅⋅⋅ ⋅ ⋅ =
⎜⎟
⎝⎠
55 5 5 5 5
5
111
3 log 3 2log log log log log
3323
abxyz=− + + + − −
.

43
3. a)
3
log 11
333
log 7 log 7 log 11=⋅ , a
3
log 7
333
log 11 log 11 log 7=⋅, так что
33
log 11 log 7
711= ;
б)
222 2
log 5 log 3 log 15 log 16 4+= < =
, то есть log
2
5+ log
2
3 < 4.
C–18
1. a) log
3
4>0, так как log
3
4>log
3
1=0;
б)
1
3
log 0,9 0> ,
так как
11
33
log 0,9 log 1 0>=.
2.
()
2
2
log 4
x
y
x
=
−
, x
2
–4 > 0 и x
2
–4 ≠ 1 при
x
2
> 4, x
2
≠ 5, так что
(
)
( ; 5) ( 5; 2) (2; 5)Dy=−∞ ∪− − ∪ ∪
(5; )∪∞.
3. См. график.
С–19
1. a)
2
2
log ( 3 ) 4xx−=;
24
3(2)xx−=
; x
2
–3x–4=0; x
1
=–1, x
2
=4;
lg(2
x+1)=0,5lg(1–3x); 2lg(2x+1)=lg(1–3x); lg(2x+1)
2
=lg(1–3x);
2
13 0,
210,
44113
x
x
x
xx
⎧
−>
⎪
+>
⎨
⎪
++=−
⎩
;
2
1
,
3
1
,
2
470
x
x
xx
⎧
<
⎪
⎪
>−
⎨
⎪
+
=
⎪
⎩
;
(
)
11
;,
23
7
0 и
4
x
xx
⎧
∈−
⎪
⎨
==−
⎪
⎩
; x=0.
2. a)
2
12
2
3log 2log 5xx−≤;
2
22
3log 2 log 5xx
−
≤ ; log
2
x=t; 3t
2
–2t–5≤0;
5
1
3
t−≤ ≤
;
2
5
1log
3
x−≤ ≤
;
3
1
;2 4
2
x
⎡
⎤
∈
⎢
⎥
⎣
⎦
;
б)
()
0
lg 1
x
x
≥
+
;
()
{
0
lg 1 0
x
x
≥
+
>
, и
()
{
0
lg 1 0
x
x
≤
+
<
;
⎩
⎨
⎧
>+
≥
11
,0
x
x
, и
{
0,
011
x
x
≤
<
+<
;
x∈(–1;0) ∪ (0;+∞)
C–20
1. a)
2
12
2
3log 2log 5xx+=;
2
22
3log 2log 5 0xx
+
−=; log
2
x=t; 3t
2
+2t–5=0;
t
1
=1, t
2
=
5
3
−
; log
2
x=1 и log
2
x=
5
3
−
; x
1
=2, x
2
=
3
1
24
;

44
б)
23
2
lg 1 lg 2xx
+=
++
; lgx=t–1,5;
22
2
0,5 0,5tt
+
=
−+
;
(
)
(
)
2
2 0,5 3 0,5
2
0, 25
tt
t
++−
=
−
; 2t
2
–5t=0; t
1
=0, t
2
=2,5; lgx=1 и lgx=–1,5; x
1
=10,
x
2
=
1
10 10
.
2. a) lg
2
x–2lgx>2; lgx=t; t
2
–2t–2>0; t<1– 3 и t>1+ 3 ; lgx<1– 3 и
lgx>1+
3
; 0<x<
13
10
−
и x>
13
10
+
;
б) 15
2x
+3⋅15
x
>10; 15
x
=t; t
2
+3t–10>0; t<–5 и t>2; 15
x
<–5 и 15
x
>2; x>log
15
2.
C–21
a)
()
33 3
3
log log 2 log 2,
log 2
xy
xy
+=+
⎧
⎪
⎨
+=
⎪
⎩
;
33
log log 18,
9
xy
xy
=
⎧
⎨
+=
⎩
;
{
18,
9
xy
x
y
=
=
−
;
()
{
918,
9
yy
xy
−=
=−
;
2
9180,
9
yy
xy
⎧
−+=
⎨
=−
⎩
1
1
6,
3
x
y
=
⎧
⎨
=
⎩
и
2
2
3,
6;
x
y
=
⎧
⎨
=
⎩
б)
cos sin
cos sin
1
4()3,
2
1
4() 2
2
xy
xy
⎧
+=
⎪
⎨
⋅=
⎪
⎩
;
cos
sin
4,
1
()
2
x
y
a
b
⎧
=
⎪
⎨
=
⎪
⎩
;
{
3,
2
ab
ab
+
=
=
;
()
{
3,
32;
ba
aa
=−
−
=
2
3,
320
ba
aa
=−
⎧
⎨
−+=
⎩
;
1
1
1,
2
a
b
=
⎧
⎨
=
⎩
и
2
1
2,
1
a
b
=
⎧
⎨
=
⎩
;
{
cos 0,
sin 1
x
y
=
=
−
и
1
cos ,
2
sin 0;
x
y
⎧
=
⎨
=
⎩
1
1
,
2
2
2
xk
yn
π
⎧
=+π
⎪
⎨
π
⎪
=− + π
⎩
и
2
2
2, ,
3
,.
xkk
ynn
π
⎧
=
±+π ∈Ζ
⎪
⎨
=π ∈Ζ
⎪
⎩
С–22
1. a)
()
1
1
x
fx
x
−
=
+
; f(x)+x⋅f(x)=1–x;
(
)
()
1
1
f
x
x
fx
−
=
+
, то есть
1
1
x
y
x
−
=
+
– об-
ратная к f(x). D(y)=(–∞;–1)∪(–1;∞); E(y)=D(f)=(–∞;–1)∪(–1;∞);
б)
()
2
2
f
xx=−, x≤0;
()
2
2
x
fx=− − , так
что
2
2yx=− − – обратная для f(x).
D(y)=E(f)=[0;
2 ]; E(y)=D(f)=[– 2 ;0].
2. f(g(–1))=–1, f(g(1))=1, f(g(3))=3, так что
g(–1)=–2, g(1)=2, g(3)=0;
D(g)=E(f)=[–1,5;0]∪(0,5;4],
E(g)=D(g)=D(f)=[–3;–1,5]∪[–1;3).
С–23
1. а) f'(x)=(3e
3+2x
)'=3e
3+2x
⋅(3+2x)'=6e
3+2x
;
45
б) f'(x)=(14
0,2–5x
)'=lg14⋅14
0,2–5x
⋅(0,2–5x)'=–5⋅14
0,2–5x
⋅ln14.
2. Уравнение касательной в точке x
0
: f(x)–f(x
0
)=f'(x
0
)(x–x
0
). Для f(x)=e
1+x
и x
0
=–1: f(–1)=1; f'(x)=e
1+x
, f'(–1)=1. Искомое уравнение y–1=x+1, y=x+2.
3.f'(x)=(x+1)'e
x–1
+(e
x–1
)'(x+1)=e
x+1
(1+x+1)=e
x+1
(x+2); f'(x)=0 при x=–2,
f'(x)>0 при x>–2, f'(x)<0 при x<–2. Так что f(x)–убывает на (–∞;–2] и f(x)
возрастает на [–2;∞).
4.
()
()
()
1
31 4 2
11
31 31
11
1
133326
3ln3 3 26
333327
x
xx
dx d
+−
++
−−
−
===−=
∫∫
.
C–24
1.a) f'(x)=
()
(
)
(
)
/
/
1
2
1
3
1
ln 2
3
1
6
2
3
x
x
x
x
−
−= =
−
−
;
б)
()
/
2
3
/
3
4
33
1
2
3
2
'log
22
ln 4 ln 4
x
x
x
x
x
fx x
x
xx
xx
⎛⎞
+
−
⎜⎟
⎛⎞
⎛⎞
⎝⎠
=−= =
⎜⎟
⎜⎟
⎛⎞⎛⎞
⎝⎠
⎝⎠
⋅− −
⎜⎟⎜⎟
⎝⎠⎝⎠
.
2. Уравнение касательной: f(x)–f(x
0
)=f'(x
0
)(x–x
0
). Для f(x)=log
3
(2x+1) и
x
0
=1: f(x
0
)=1,
()
()
2
'
ln 3 2 1
fx
x
=
⋅
+
,
(
)
0
2
'
3ln3
fx=
Искомое уравнение:
()
2
11
3ln3
yx−= −
;
22
1
3ln3 3ln3
x
y =−+
.
3.
() ( )
()
()
()
(
)
() ()
/
/
2
2ln 1
1
'lg1ln1
ln10 1 ln10 1
x
fx x x
xx
+
=+−+= −
⋅
+⋅+
. f'(x)=0
при 2lg(x+1)–1=0,
110x += , 10 1x
=
− . f'(x)>0 при 10 1x >−и
f'(x)<0 при
10 1x <−; f(x) – возрастает на
)
10 1;
⎡
−
∞
⎣
и убывает на
(
1; 1 0 1
⎤
−−
⎦
.
С–25
1.
()
3/ 3/ 3/ 1,5/
11
'(())(())()()fx x x
x
x
−−
=+=+=
31 2,5
31,5xx
−−
− .
2.
5
4
16,08 32,15 0,0006−≈
.
3.
11
1
1
1
11
e
ee
e
e
xe
Sxdx
ee
++
−
===
++
∫
.
С–26
1. f'(x)=(e
–0,4x
)'= –0,4⋅e
–0,4x
= –0,4f(x). Так что y'= –0,4y – искомое уравне-
ние.
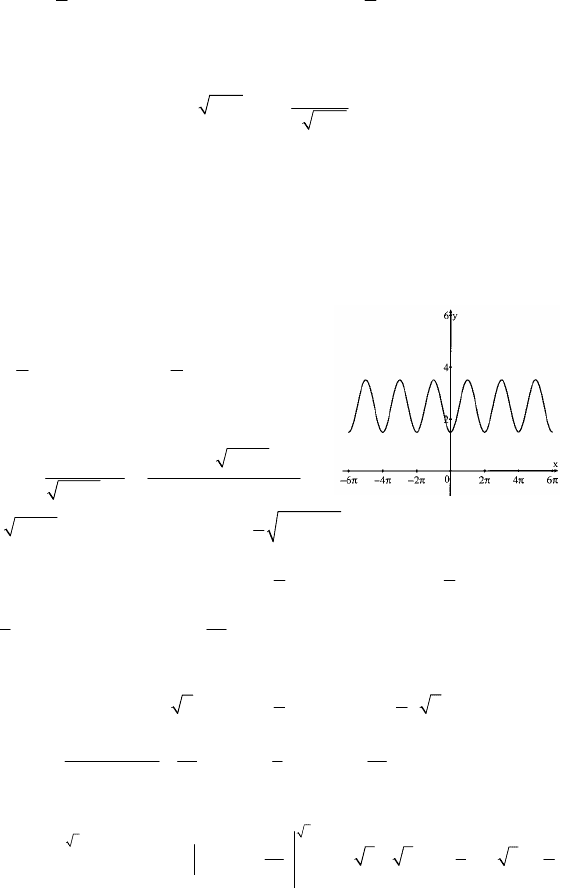
46
2. Общее решение уравнения f'(x)=f(x)⋅ln3: f(x)=C⋅e
xln3
=c⋅3
x
, а так как
f(1)=9, то 9=C⋅3, C=3, и f(x)=3
x+1
– искомое решение.
3.
1
''
4
yy=−
. Общий вид решения:
12
1
cos
2
yC xC
⎛⎞
=⋅ +
⎜⎟
⎝⎠
, где C
1
, C
2
∈R.
Вариант 7
С–1
1.а) является, т.к.
()
()
()
/
1
'= 1+2= =
21
Fx x fx
x
−
−
, для всех x∈(1;∞);
б) нет, так как F'(x)=(3x
2
–1)'=6x≠f(x) для некоторых x∈(–∞;∞).
2. а) F'(x)=(2–sin
2
x+cos
2
x)'=–2sinxcosx–2sinxcosx=–2sin2x=f(x), для всех
x∈(0;2), так что F(x) – первообразная для f(x) на (0;2);
б) F'(x)=((x–1)
4
)'=4(x–1)
3
=4x
3
–12x
2
+12x–4≠f(x), но вероятно в условии
опечатка и для f(x)=4x
3
–12x
2
+12–4 F(x)– является первообразной на
(–∞;∞).
С–2
1. Общий вид первообразных для
h(x)=sinx: H(x)=–cosx+C, а так как
2
3
H
π
⎛⎞
=
⎜⎟
⎝⎠
, то
2cos
3
C
π
=− +
;
C=2,5; H(x)=2,5–cosx.
2. а)
()
62
611
x
fx
x
−
=
−+
()
(
)
62611
611
xx
x
−
−−
=
−−
=
611x=−−, так что
() ()
3
1
61
9
Fx x x C
=
−+ − + ;
б) f(x)=sinxcosxcos2xcos4x;
()
1
sin 2 cos 2 cos 4
2
f
x xxx
=
=
1
sin 4 cos 4
4
x
x =
=
1
sin8
8
x
. Так что
()
1
cos
64
Fx x C
=
−+
C–3
a)
(
)
(
)
sin 1,5 1 ,
f
xxx=−+
() ()
22
cos 1,5 1
33
Fx x x x C
=
−−++;
б)
()
()
2
2
1
2
3cos 7
x
gx
x
=+
−
,
() ()
3
1
7
36
x
Gx tgx C
=
−+ +.
C–4
a)
()
3
3
13
1
22
0
01
1
1
23 3 1333
33
x
xdx x dx x x
⎛⎞
+− =+− =+−−+=
⎜⎟
⎜⎟
⎝⎠
∫∫
2
23 1
3
−
;
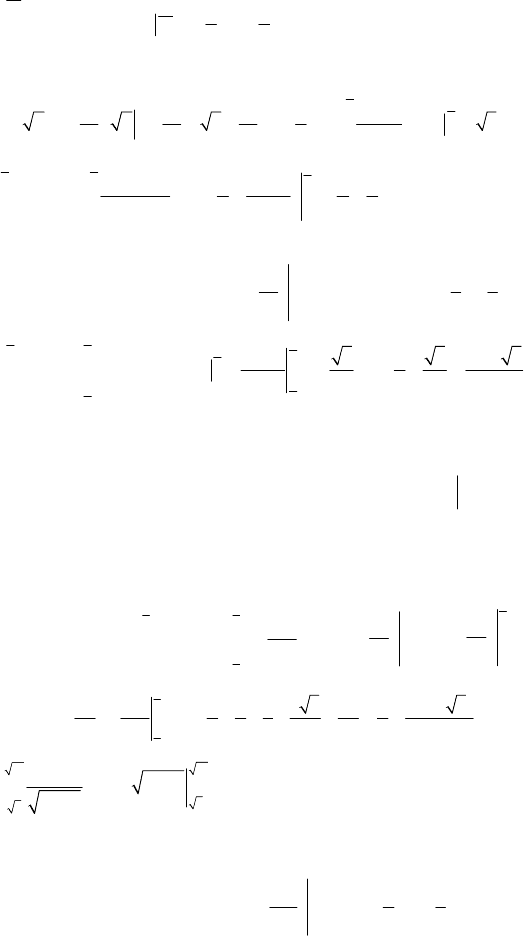
47
б)
()
4
4
3
3
11
sin cos 1
22
xdx x
π
π
π
π
−==−+=
∫
.
С–5
а)
9
9
1
1
10 10 10 2
59986
3333
xdx x x==⋅−=
∫
; б)
3
3
2
0
0
tg 3
cos
dx
x
x
π
π
==
∫
;
в)
44
4
2
00
0
1cos2 sin2
cos
224
xx x
xdx dx
ππ
π
+
⎛⎞
==+=
⎜⎟
⎝⎠
∫∫
1
84
π
+
.
C–6
a)
()
3
3
3
22
1
1
11
43 2 3 189923 1;
333
x
Sxxdxxx
⎛⎞
= −− = − − = −−−++ =
⎜⎟
⎜⎟
⎝⎠
∫
б)
6
4
4
6
0
0
6
6
sin 2 3 1 3 6 3 3
sincos2cos 1
22244
x
xdx xdx
π
π
π
π
π
π
−
+=−+=−++−=
∫∫
.
С–7
Пусть S(t) – уравнение пути, тогда S'(t)=V(t) и
() () ()
()()
20 20
20
32 4
10
10 10
20 10 10 0,008 5 0,002S S V t dt t t dt t t−= =− =− =
∫∫
2000 –
– 500 – 320 + 20 = 1200 (м). Далее, a(t) = V'(t) = 10 – 0,024t
2
и a(20)=
= 10 – 9,6 = 0,4 (м/с
2
).
С–8
1. S=
() ()
13
0
24
1
10
2
2
11cos
3
x
x
dx x dx dx
−
π
++−+
∫∫∫
=
0
2
1
2
x
x
−
⎛⎞
+
⎜⎟
⎜⎟
⎝⎠
+
1
2
2
0
2
x
x
⎛⎞
−
⎜⎟
⎜⎟
⎝⎠
+
3
4
1
2
32
sin
23
x
π
+
π
=
11133373(2 3)
1
228 4 2 8 4
−
−+−− + =+
ππ π
.
2.
10
10
2
2
5
5
2
21642
1
x
dx x
x
=−=−=
−
∫
.
С-9
1. Это тело вращения с площадью поперечного сечения S(x)=π(4+4z
2
).
Так что
()
1
3
1
2
0
0
44
44 4 4
33
z
Vzdzz
⎛⎞
⎛⎞
=π⋅ + =π + =π + =
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
∫
1
5
3
π
.
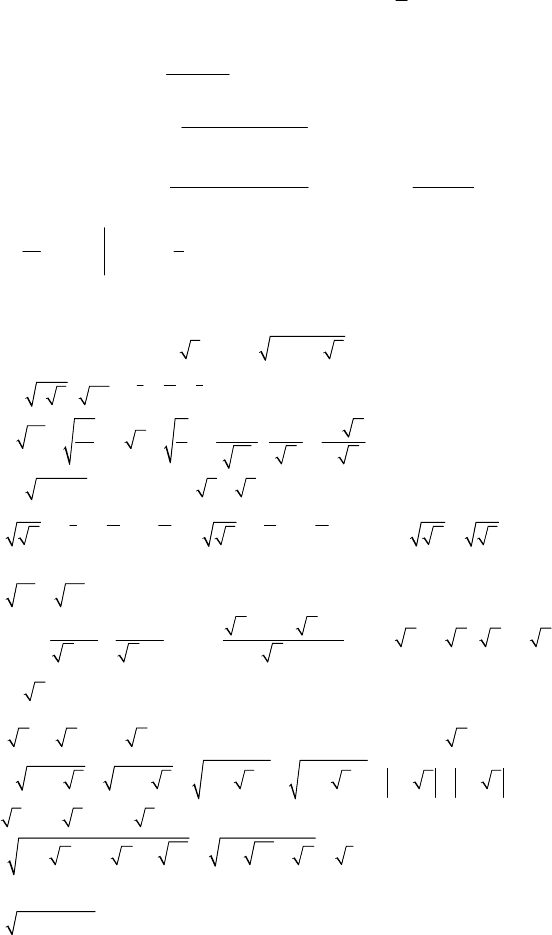
48
2. Разобем трапецию на полоски длиной ∆x=
h
n
. Площадь такой
полоски приближено равна S
x
≈l
x
∆x, где l
x
– длина верхнего основания
полоски
()
x
x
ch
lbab
n
−
+
=+ −
. Так что давление воды на эту полоски
равно
(
)
(
)
.
xx
abxch
PSxg bx x
n
⎛−−+⎞
≈⋅≈ + ∆
⎜⎟
⎝⎠
Теперь давление на одну
сторону:
(
)
(
)
(
)
10
5
45
6
5
c
ch
abxchx x
P g bx dx x x gdx
n
−
⎛−−+⎞⎛ −⎞
=+ =+ =
⎜⎟⎜⎟
⎝⎠⎝⎠
∫∫
10
32
5
41
308
15 3
g
xx g
⎛⎞
=+=⋅
⎜⎟
⎝⎠
.
С–10
1. Неверно, так как
533 0
−
<
, а 52 30 3 0
−
> .
2. а)
113
1
3
55
3155
33 27 3 3 3 3 3;⋅=⋅⋅==
б)
3
3
3
3
1 1 212172
2:2 : 3,5
2
222
2
2
⎛⎞⎛⎞
−− ⋅
−−= ==
⎜⎟⎜⎟
⎜⎟⎜⎟
⎝⎠⎝⎠
.
3. а)
3
20,991 2,7585≈ ; б)
3
4
5 5 3, 2053+≈ .
4.
15 1
3
630 30
22 2 32== = , а
11
5
10 30
33 27,== так что
3
2 >
5
3 .
С–11
1.
3
4
34
aa≥
равносильно а≥|a| и справедливо только при а≥0.
2. а)
44
13
2
11xx
+=
−+
;
44
13 3
2;
1
xx
x
++ −
=
−
4
42;
x
x=
4
2;
x
x=
4;
x
x=
2
0,
;
16
x
x
x
≥
⎧
⎨
=
⎩
x=0 и x=16.
б)
36
310;xx−=
6
,0;xaa
=
≥ a
2
–3a–10=0; a= –2 и a=5;
6
5;x
=
6
5.x =
3.а)
()()
22
423 423 13 13 1313−++=− ++ =−++=
31 3123;=−++=
б)
()()
4
8
4
42
4
44
4
11 1 11.aaa aa−++=−+==
С–12
1.
2
3321;xx x++=+
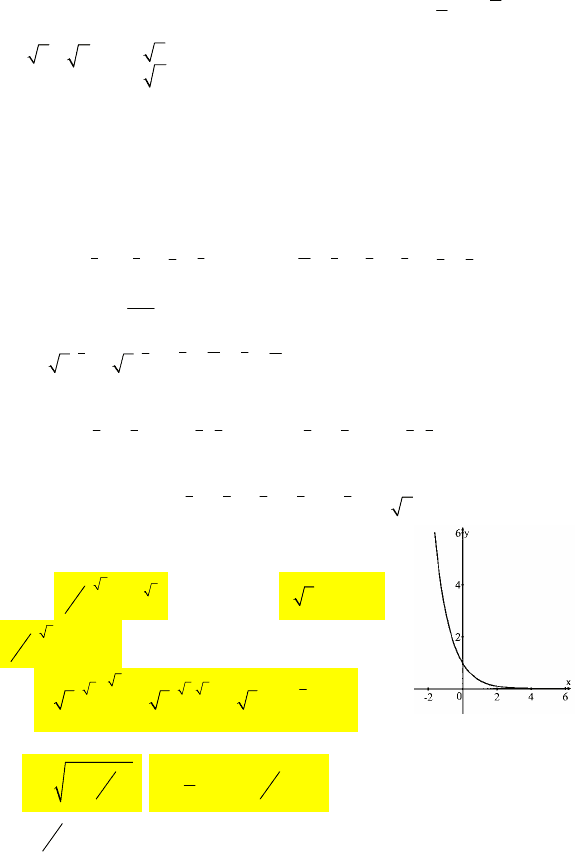
49
()
2
2
210,
;
3321
x
xx x
+≥
⎧
⎨
++= +
⎩
2
0,5,
;
320
x
xx
≥−
⎧
⎨
+
−=
⎩
0,5,
2
;
1 и
3
x
xx
≥−
⎧
⎪
⎨
=− =
⎪
⎩
2
.
3
x
=
2.
3
3
1,
;
7
xy
xy
⎧
−=
⎨
−=
⎩
3
3
,
;
x
a
yb
⎧
=
⎨
=
⎩
()
()
22
1,
;
7
ab
aba abb
−=
⎧
⎪
⎨
−
++ =
⎪
⎩
22
1,
;
7
ab
aabb
−=
⎧
⎨
+
+=
⎩
()()
2
2
1,
;
11 7
ab
bbbb
=+
⎧
⎨
++++=
⎩
2
1,
;
20
ab
bb
=+
⎧
⎨
+
−=
⎩
12
12
1, 2,
и ;
21
aa
bb
=− =
⎧⎧
⎨⎨
=− =
⎩⎩
12
12
1, 8,
и ;
81
xx
yy
=− =
⎧⎧
⎨⎨
=− =
⎩⎩
С–13
1.а)
51 3 10548
113
1
222
33 8 3333
444
15 45 : 75 2 4 3 5 3 5 3 5 2 2
−−
−−−
⋅+⋅=⋅⋅⋅⋅⋅+⋅=
031
1
35 2 2
125
−
=⋅ += ;
б)
()()
213
1
11
23 11
5107
14
57
33bb bb bb bb b=⋅ ⋅⋅ === при b=3.
2. а) верно при а≥0; б) верно при всех а.
3.
13 13 13 13
33
2 2 22 2 2 22
xyxxyy xyxxyy
⎛⎞⎛ ⎞⎛⎞⎛ ⎞
⎜⎟⎜ ⎟⎜⎟⎜ ⎟
+−++−++=
⎜⎟⎜ ⎟⎜⎟⎜ ⎟
⎝⎠⎝ ⎠⎝⎠⎝ ⎠
3939 3
2222 2
22.
x
yxy x xx=++−= =
С–14
1. См. график.
2. а)
()
5
5
1
3,
3
−
= а так как 52,25,−>− то
()
5
2,25
1
3;
3
−
>
б)
() () ()
33
3333
1,5
2
33333,
⋅
⎛⎞
====
⎜⎟
⎝⎠
так
что числа равны.
3.
()
1
1;
2
x
y =−
1
10;
2
x
⎛⎞
−≥
⎜⎟
⎝⎠
(
)
1
1;
2
x
≤
x≥0, так что D(y)=[0;∞), а так
как
()
1
0,
2
x
> то у<1 и E(y)=[0;1).
C–15
1. а) 0,5
3–2x
+3⋅0,25
1–x
=7; 0,5⋅0,5
2–2x
+3⋅0,5
2–2x
=7; 0,5
2–2x
=2; 2–2x=–1; 2x=3;
x=1,5;
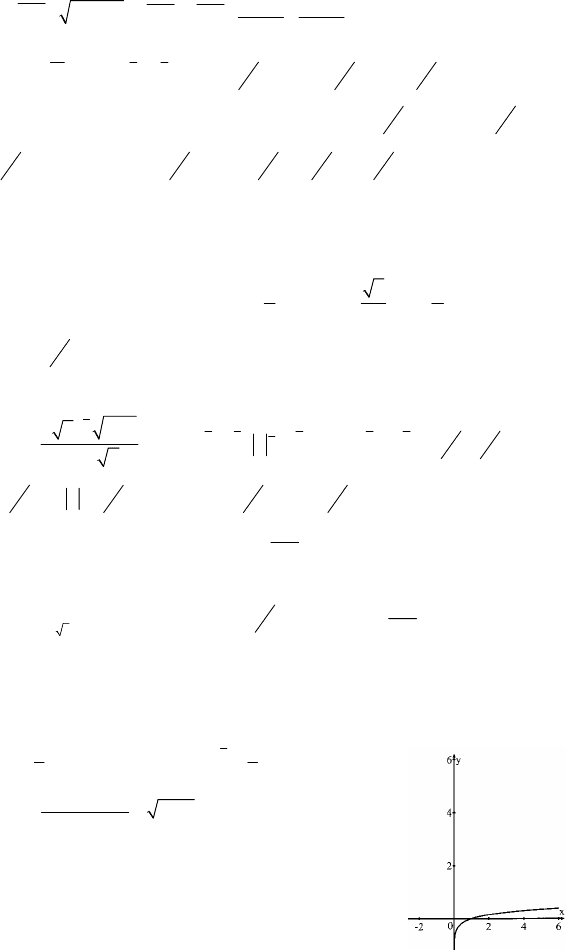
50
б)
63
4
21
5 = 125
x
x
x
+
+
;
63
63
4
5=5;
x
x
x
+
+
6363
=;
4
xx
x
+
+
(6x+3)(x–4)=0;x
1
=4,x
2
=–0,5.
2. а)
12
1
23
25 125 ;
x
+−
<
1
2
2
55;
x
+
−
<
1
22;
x
+
<−
1
4;
x
<
−
1
0;
4
x
−
<<
б) 4
x
⋅5+2⋅25
x
≤7⋅10
x
; 5⋅2
2x
+2⋅5
2x
–7⋅2
x
⋅5
x
≤0;
(
)
(
)
2
22
5270;
55
xx
⋅
+−⋅ ≤
(
)
2
;
5
x
t= 5t
2
–7t+2≤0;
2
1;
5
t
≤
≤
(
)
(
)
(
)
0
22 2
;
55 5
x
≤≤ 0 ≤ x ≤1.
C–16
1. a) 2⋅3
x–6
+6⋅9
0,5x–2
=56; 2⋅3
x–6
+6⋅9⋅3
x–6
=56; 3
x–6
=1; x=6;
б)
2
cos 2 cos
443;
xx
+=
22
2cos 1 cos 0,5
424 3;1
xx−−
+⋅ =
2
cos 0,5
4;
x
t
−
=
t
2
+2t–3=0;
t
1
=–3 и t
2
=1;
2
cos 0,5
41;
x−
=
2
1
cos ;
2
x =
2
cos ;
2
x =±
,.
4
xnn
π
=
+π ∈Ζ
2.
()
1
1
4+
2
x
x
−−
–8≥0; 4
x
+2⋅2
x
–8≥0; 2
x
=t; t
2
+2t–8≥0; t≤–4 и t≥2; 2
x
≥2; x≥1.
C–17
1.
1
1
3111
6
23
1
3
1
3
2222
3
0,5
77
77
log = log 7 5
5
abc
abc d k
dk
−−
−
⎛⎞
⎜⎟
⋅⋅ ⋅⋅ ⋅ ⋅
⎜⎟
⎝⎠
=
7
3
1
log
23
a
+
+
+
7
1
log
3
b +
77 7 7
111
log log 5 log log .
222
cdk−− −
2.
3
30 30 30 30
30
log 8 log 2 3log 2 3log
35
=== =
⋅
(
)
30 30 30
3 log 30 log 3 log 5
=
−− =
= 3(1–a–b).
3. a)
2
6
3
93 333
3
24
1
log 24 log 4 2log 24 6log 4 log log 9 2;
2
4
−= −⋅= ==
б)
log 2
11
11 11 2 11 11 2 11
log 2 log 7 log 7 log 7 log 2 log 7 log 7
72=2 2=2 2=
⋅
−− −
11 11
log 7 log 7
22− =0.
С–18
1.а) log
0,3
4<0, так как 0,3<1, a 4>1; б)
1
lg 3 0,
3
−>
так как
1
3
1
lg 3 lg10 .
3
>=
2.
()
12
1
7;
log 3
yx
x
=+−
−
30,
31,;
70
x
x
x
−>
⎧
⎪
−≠
⎨
−≥
⎪
⎩
3,
4,
7
x
x
x
>
⎧
⎪
≠
⎨
≤
⎪
⎩
D(y)=(3;4)∪(4;7].
3. См. график.
