Saltzman B. (editor) Anomalous Atmospheric Flows and Blocking
Подождите немного. Документ загружается.


284
J.
S.
FREDERIKSEN
TABLE
I.
PHASE
FREQUENCIES, GROWTH
RATES,
AND
PERIODS~
1
2
3
4
5
6
7
8
9
10
II
12
13
14
I5
16
17
I8
19
20
21
22
A
A
B
A
B
A
B
A
C
B
C
B
F
A
F
C
F
B
E
C
C
D
0.30486
0.25510
0.13536
0.20759
0.16698
0.35928
0.10662
0.42264
0.07 1627
0.16149
0.
I2252
0.19731
0.08983
0.55
167
0.03059
0.09676
0.05758
0.24884
0.02386
0.
I28288
0.08
1
154
0.0
109.7
91.8
48.7
74.7
60.1
129.3
38.4
152.2
25.8
58.1
44.
I
71.0
32.3
198.6
11.0
34.8
20.7
89.6
8.6
46.2
29.2
0.0
3.3
3.9
7.4
4.8
6.0
2.8
9.4
2.4
14.0
6.2
8.2
5.1
11.1
1.8
32.7
10.3
17.4
4.0
41.9
7.8
12.3
m
0.06796
0.06638
0.06246
0.06 195
0.06125
0.0599
1
0.05978
0.05499
0.05217
0.05216
0.05090
0.04498
0.04 128
0.0392
I
0.03593
0.03581
0.03454
0.03409
0.03358
0.03 I37
0.03
136
0.02725
0.4270
0.4171
0.3924
0.3892
0.3848
0.3764
0.3756
0.3455
0.3278
0.3277
0.3 I98
0.2826
0.2594
0.2464
0.2258
0.2250
0.2 170
0.2142
0.2 I09
0.1971
0.1970
0.1712
~~~
____
~ ~
____
~~ ~
ff
Data
are
for
all
growing
modes,
from
the fastest to the
first nonpropagating
mode
for
Case
1.
with modes of this type being onset-of-blocking modes which initiate the
blocking process. Evidence in support of this hypothesis will
be
presented in
the following sections.
As
shown in Table
I,
Modes
5,
7,
10,
12, and 18 of
Case
1
are also similar to the above modes. On the whole, most of these
modes have periods somewhat longer than those of the monopole cyclogen-
esis modes but shorter than those of the class of Pacific and Atlantic onset-
of-blocking dipole modes now to
be
considered.
2.5.3.
Pacific
and
Atlantic
Onset-oJBlocking Dipole Modes
(Class
C).
The typical modes
of
this class are the ninth fastest growing mode for
Case
I,
for which the upper layer disturbance streamfunction is shown in Fig.
4,
and Mode
1
of
Case
3
shown in Fig.
7
of Frederiksen (1982a). They have
longer periods than the Pacific onset-of-blocking dipole modes and have
dipoles over a larger area
of
the
globe,
in particular in both the Pacific and
Atlantic oceans. Modes
1 1
and
16
of
Case
1
also
are qualitatively quite
similar to these patterns; Modes
20
and 2
1
of
Case
1
also
show many of the
same characteristics.
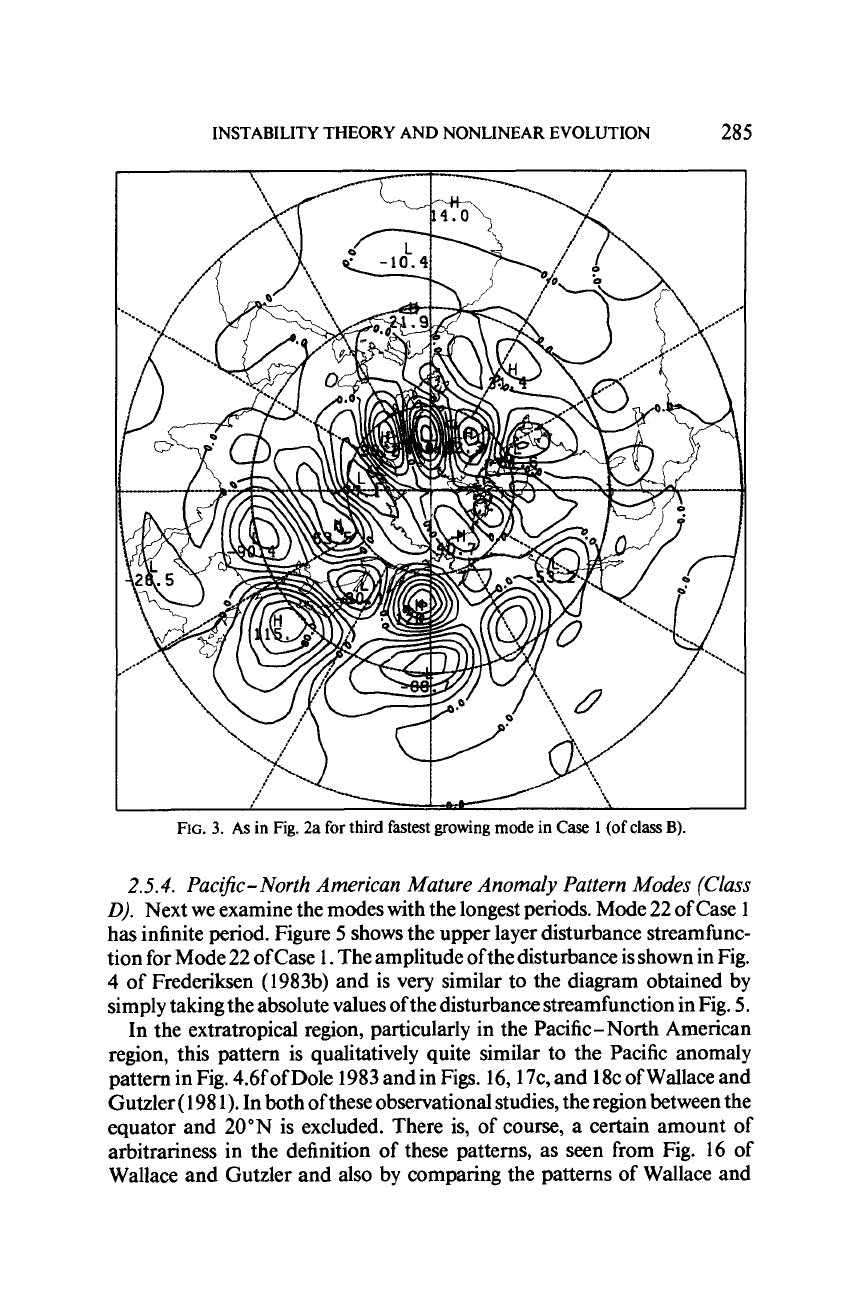
INSTABILITY THEORY AND NONLINEAR EVOLUTION
285
FIG.
3.
As
in
Fig.
2a
for
third
fastest
growing
mode
in
Case
1
(of
class
B).
2.5.4.
PaciJic- North American Mature Anomaly Pattern Modes (Class
0).
Next we examine the modes with the longest periods. Mode
22
of Case
1
has infinite period. Figure
5
shows the upper layer disturbance streamfunc-
tion for Mode
22
of Case
I.
The amplitude ofthe disturbance is shown in Fig.
4
of
Frederiksen (1983b) and is very similar to the diagram obtained by
simply taking the absolute values ofthe disturbance streamfunction in Fig.
5.
In the extratropical region, particularly in the Pacific-North American
region, this pattern is qualitatively quite similar to the Pacific anomaly
pattern in Fig. 4.6f of Dole 1983 and in Figs. 16,17c, and I8c of Wallace and
Gutzler
(
198
I).
In both of these observational studies, the region between the
equator and
20"N
is excluded. There is, of course, a certain amount
of
arbitrariness in the definition of these patterns, as seen from Fig.
16
of
Wallace and Gutzler and also by comparing the patterns of Wallace and
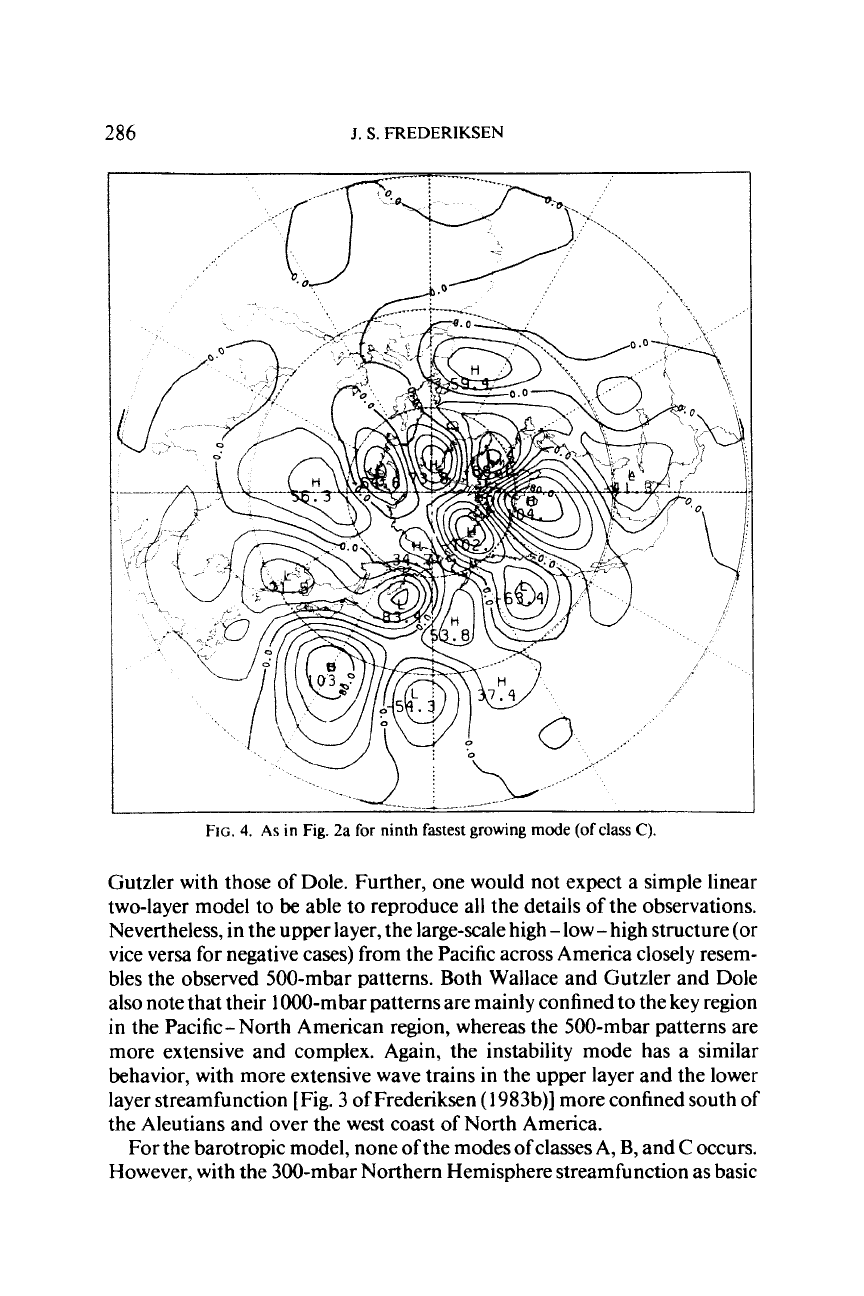
286
J.
S.
FREDERIKSEN
FIG.
4.
As
in
Fig.
2a
for
ninth
fastest
growing
mode
(of
class
C).
Gutzler with those of Dole. Further, one would not expect a simple linear
two-layer model to
be
able to reproduce all the details of the observations.
Nevertheless, in the upper layer, the large-scale high -low
-
high structure (or
vice versa for negative cases) from the Pacific across America closely resem-
bles the observed 500-mbar patterns. Both Wallace and Gutzler and Dole
also note that their 1000-mbar patterns are mainly confined to the key region
in
the Pacific-North American region, whereas the 500-mbar patterns are
more extensive and complex. Again, the instability mode has a similar
behavior, with more extensive wave trains in the upper layer and the lower
layer streamfunction [Fig.
3
of Frederiksen
(
1983b)l more confined south of
the Aleutians and over the west coast of North America.
For the barotropic model, none
of
the modes of classes A,
B,
and
C
occurs.
However, with the 300-mbar Northern Hemisphere streamfunction as basic
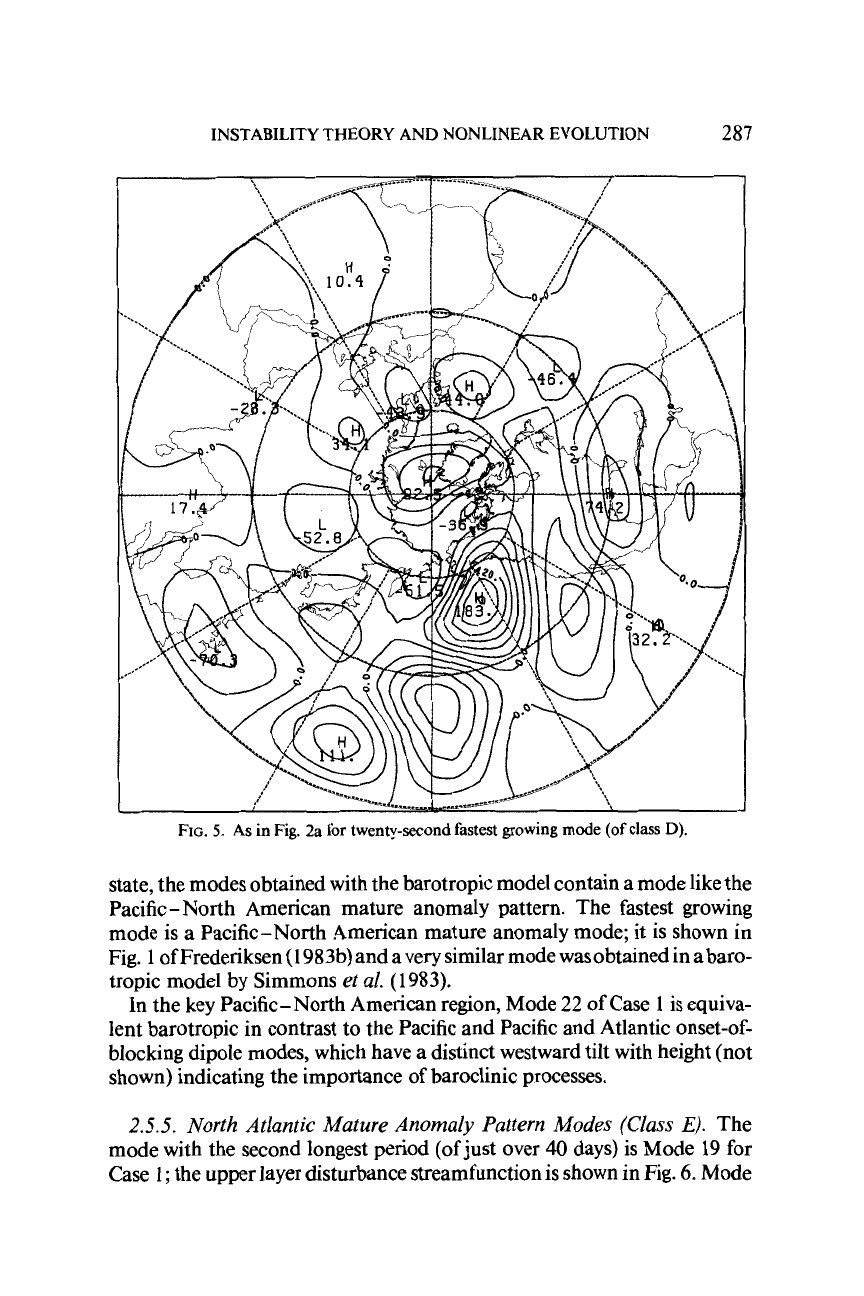
287
INSTABILITY THEORY AND NONLINEAR EVOLUTION
FIG.
5.
As
in
Fig.
2a
for
twenty-second fastest growing mode
(of
class
D).
state, the modes obtained with the barotropic model contain a mode like the
Pacific- North American mature anomaly pattern. The fastest growing
mode is a Pacific-North American mature anomaly mode; it is shown in
Fig.
1
of Frederiksen
(1
983b) and a very similar mode was obtained in a baro-
tropic model by Simmons
et al.
(
1983).
In the key Pacific-North American region, Mode
22
of Case
1
is equiva-
lent barotropic in contrast to the Pacific and Pacific and Atlantic onset-of-
blocking dipole modes, which have a distinct westward tilt with height (not
shown) indicating the importance of baroclinic processes.
2.5.5.
North Atlantic Mature Anomaly Pattern Modes (Class
E).
The
mode with the second longest period (of just over
40
days) is Mode 19 for
Case
1
;
the upper layer disturbance streamfunction is shown in Fig.
6.
Mode
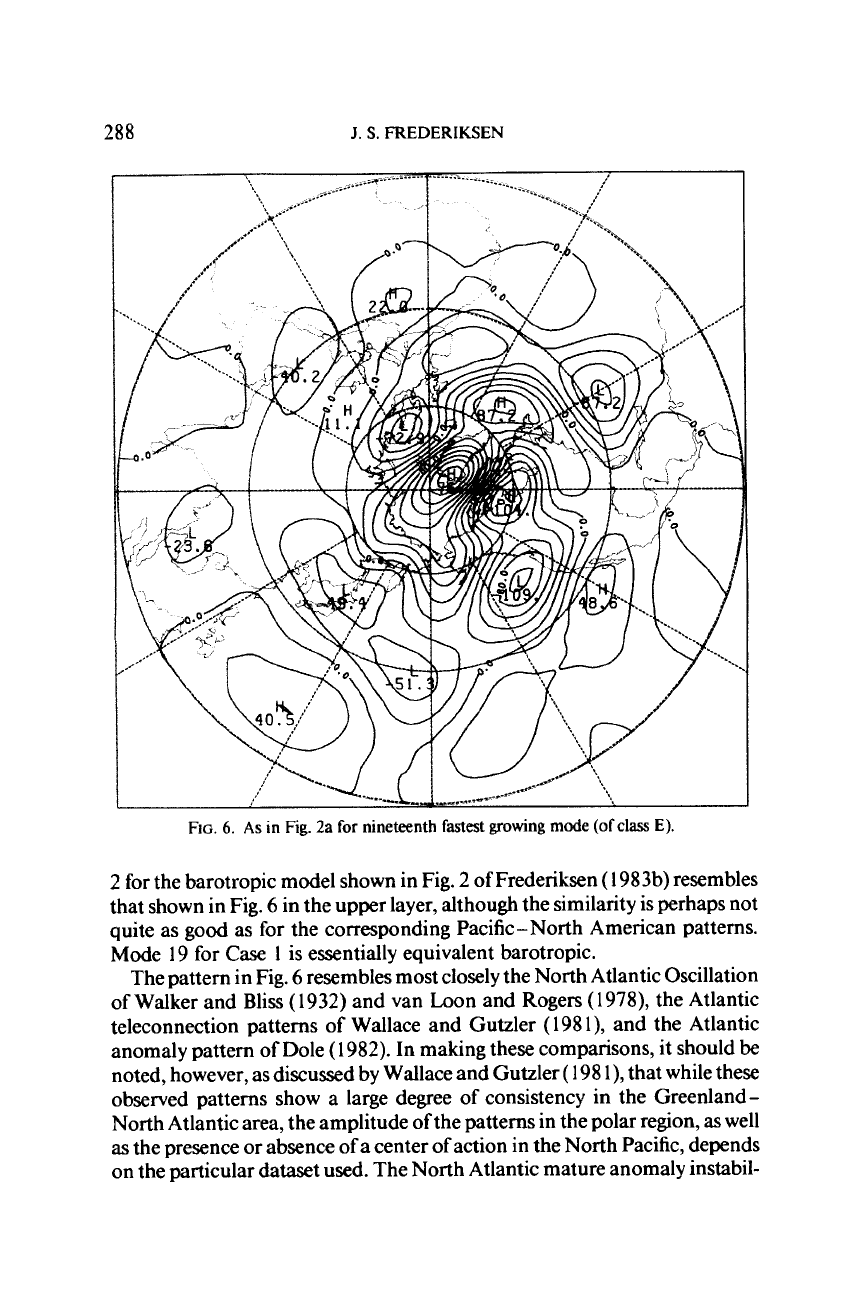
288
J.
S.
FREDERIKSEN
FIG.
6.
As
in
Fig.
2a
for
nineteenth
fastest
growing mode
(of
class
E).
2
for the barotropic model shown in Fig.
2
of Frederiksen
(
1983b)
resembles
that shown in
Fig.
6
in the upper layer, although the similarity is perhaps not
quite as
good
as for the corresponding Pacific
-
North American patterns.
Mode 19 for
Case
1
is
essentially equivalent barotropic.
The pattern in Fig.
6
resembles most closely the North Atlantic Oscillation
of Walker and Bliss
(1932)
and van Loon and Rogers (1978), the Atlantic
teleconnection patterns
of
Wallace and Gutzler
(198
l),
and the Atlantic
anomaly pattern of Dole
(
1982). In making these comparisons, it should be
noted, however, as discussed by Wallace and Gutzler
(
198 l),
that while these
observed patterns show a large degree of consistency in the Greenland-
North Atlantic area, the amplitude
of
the patterns in the polar region,
as
well
as
the presence or absence
of
a center of action in the North Pacific, depends
on the particular dataset
used.
The North Atlantic mature anomaly instabil-

INSTABILITY
THEORY
AND
NONLINEAR
EVOLUTION
289
ity mode appears to bear closest resemblance to the sea level pressure anom-
aly pattern in Fig.
1
1
of van Loon and Rogers (1978).
2.5.6.
IntermediateModes (Class
F).
Among the modes in Table
I,
there
is also a group whose properties, in qualitative terms, are intermediate be-
tween the onset-of-blocking dipole modes and the mature anomaly pattern
modes discussed above. Mode 15
of
Case
1
has the third largest period
(of
-
30 days); Fig. 6
of
Frederiksen (1983b) shows the disturbance stream-
function. As seen there, this mode appears to have characteristics of both of
the major mature anomaly modes previously discussed. However, the scale
of the centers making up the mode appears on the whole to be smaller.
Modes 17 and
1
3 of Case
1
have similar structures and periods of
1
7.4 and
1
1.1
days, respectively; Fig. 7 of Frederiksen (1983b) shows the perturbation
streamfunction for Mode 17. These modes have properties and, in particu-
lar, scales intermediate between the mature anomaly pattern modes and the
Pacific and Atlantic onset-of-blocking modes.
3.
TIME EVOLUTION
OF
OBSERVED MATURE
ANOMALIES
At the time of the study of Frederiksen
(
1982a), there appeared to be no
systematic statistical studies on the observed time evolution of mature
anomalies such
as
blocks. Nevertheless, it seemed reasonable that the slower
propagating modes with dipoles in the Pacific and Atlantic regions, called
class
B
and C modes here, would initiate the process of the formation of
mature anomalies such as blocks further downstream.
The thesis of Dole (1982), parts
of
which have been published in Dole
(1983) and also in this volume, provided important insights into many
aspects
of
observed mature anomalies, including their time evolution. Here
we shall relate some
of
the instability solutions of Section 2 to Dole’s obser-
vations.
In our discussion
of
Dole’s studies, we shall concentrate on anomalies
corresponding to the Pacific-North American pattern, since this is the case
for which he gives the most extensive analysis. Similar results also hold for
the North Atlantic (and northern Soviet Union) anomalies, which he also
treats in lesser detail. Dole finds in his studies not only positive anomalies in
the key region corresponding to blocking, but also negative anomalies. He
notes that the two extreme stages of the index cycle (Namias, 1950) appear in
his analyses
as
opposite phases of
a
single basic anomaly pattern, with high
zonal index corresponding to negative anomaly and low zonal index corre-
sponding to positive anomaly, such as caused by blocking.
Figure 4.6
of
Dole (1983) shows the time evolution of composite analyses

290
J.
S.
FREDERIKSEN
of
15
low-pass-filtered positive anomaly cases at
500
mbar in the Pacific. The
sequence starts
4
days before (on day
-4)
the appearance (on day
0)
of
the essentially stationary large-scale positive anomaly in the key region in the
north central Pacific and finishes
6
days thereafter. The corresponding se-
quences for unfiltered anomalies between days -3 and
0
are shown in Fig.
4.7 of Dole (1983). For the period leading up to the appearance of the
positive anomaly in the key region, referred to in Frederiksen
(1
982a) as the
onset-of-blocking period, Dole notes that the “sequence
of development
suggests that the initial rapid growth of the main centre is primarily asso-
ciated with the propagating intensifying disturbance which originates in
mid-latitudes near Japan.” He also notes that “this disturbance continues to
intensify as it becomes quasi-stationary over the key region.” The dipole
wave train that appears in Fig.
4.7
of Dole (1983) at day -3 is qualitatively
very similar to that in our Fig. 3 and as well to that in Fig. 6a of Frederiksen
(
1982a).
Further evidence that modes
of
class
B
are involved in the initial period
may
be
obtained from Fig.
5.10
of
Dole (1982), which shows longitude-
pressure cross sections at
45”
and 20”N of the unfiltered Pacific composite
anomalies at I-day intervals between days -3 and
0.
The dipole nature of the developing anomaly is clearly evident particu-
larly at day -3, and the zonal scale of the anomaly at day -3 is practically
the same as shown in Fig.
6
of Frederiksen (1982a) and in our Fig. 3. The
developing anomaly has a definite westward tilt with height, as do the class
B
modes. Dole notes: “This feature has pronounced westward tilts with height
during this period, suggesting that a substantial baroclinic contribution is
involved in its amplification.”
Following day
0,
the development of the 500-mbar height anomaly
is
as
shown in Fig.
5.
Id-
f
of Dole
(
I982), with the anomalies being largely equiv-
alent barotropic during this
period.
Intensification
of
the centers occur with
little phase propagation and by day
4
and especially at day
6
the Pacific-
North American pattern is established.
The above observational and theoretical results suggest that the develop-
ment of mature anomalies such as blocks may be thought of as approxi-
mately consisting of two stages, which, for the Pacific- North American
pattern, are as follows:
1.
A
rapidly growing and relatively rapidly eastward-propagating dipole
(class
B)
disturbance which tilts westward with height forms in the Pacific
Ocean
-
East
Asia region through the combined baroclinic
-
barotropic in-
stability
of
the three-dimensional basic state.
As
the disturbance grows, the
regions of largest amplitude propagate into the central Pacific and the distur-
bance increases its zonal scale, becoming quasi-stationary and essentially

INSTABILITY
THEORY
AND NONLINEAR
EVOLUTION
29
1
equivalent barotropic through the operation of nonlinear effects. At this
stage the mode has a structure reminiscent of class
D
modes.
2.
The (nonlinear analog of
A)
class
D
mode amplifies without phase
propagation and through the operation of largely equivalent barotropic ef-
fects to form the large-amplitude mature Pacific- North American anomaly
pattern.
We have concentrated in this section on the composite results of Dole
(
1983), which present a very clear-cut example of the change in the horizon-
tal and vertical structures of the anomaly pattern, starting upstream of the
key region with the formation of westward-tilting smaller scale dipole distur-
bances. The importance of transients in the development of blocks has also
been pointed out by many other authors, e.g., Lejenas (1 977), Green
(
1977),
Austin
(
1980), Youngblutt and Sasamori (1 980), Tucker
(
1979), Illari and
Marshall (1983), Colucci (1982), Hansen and Chen (1982), and Shutts
(1983). Hansen and Chen, in particular, note that in their observational
studies of blocking, intense upstream cyclogenesis preceded the growth of
the blocking ridge. Further, “the nonlinear transfer of kinetic energy from
baroclinically active cyclone-scale waves to the planetary-scale waves pro-
vided the major source of kinetic energy for the block.” Lejenas
(
1977) notes
the importance of the combination of barotropic and baroclinic instability
during the formation
of
blocks. Barnett (1984), in an observational study,
also
finds support for instability normal modes playing important roles in
the generation of anomaly patterns.
For the Southern Hemisphere, Frederiksen (1984, 1985) has carried out
three-dimensional instability studies for climatological flows and for synop-
tic flows leading to the formation
of
blocks in the Australian
-
New Zealand
area, as well as cyclogenesis in a number ofregions. Instability theory appears
to be able to pick out many of the important developments. In particular,
dipole instability modes are produced in
or
slightly upstream of the blocking
region. Lejenas (1 984), in an observational study
of
Southern Hemisphere
blocking, also finds support for dipole instability modes being responsible
for the majority of blocking episodes while the additional influence of forc-
ing controls the duration.
4. NONLINEAR SIMULATION
Next, we relate the results of numerical simulations of evolving baroclinic
waves to the properties of the instability solutions and to observations of
developing anomalies. We shall primarily consider a study by Frederiksen
and Pun
(
1985) of nonlinear baroclinic waves growing on an initial three-di-

292
J.
S.
FREDERIKSEN
mensional basic Northern Hemisphere flow in a multilevel primitive equa-
tion model.
4.1.
Model Details
This study was camed out using the a-coordinate spherical primitive
equation spectral model developed by Bourke (1974) and Bourke
et
al.
(1977), and used by Frederiksen
(
198
la,b) for studying life cycles of nonlin-
ear baroclinic waves growing on initially zonally averaged flows. The equa-
tions for vorticity, divergence, thermodynamics, and continuity are de-
scribed in Section 2 of Frederiksen
(
198
1
a). Since initial three-dimensional
basic states are considered constant, forcing functions are included on the
right-hand sides of
Eqs.
(2.la)-(2.ld) of Frederiksen (1981a). The model
also includes topography,
so
the term
-OW.
is added to the right-hand side
of the divergence equation, where
a.
is the geopotential height ofthe North-
em
Hemisphere topography.
A five-level version of the model with five equispaced
a
levels of
a
=
0.1,
0.3,0.5,0.7, and 0.9 and a rhomboidal truncation scheme with
a
truncation
number
J
=
21 are used. The model includes biharmonic diffusion and
surface drag. For the basic state we take the monthly averaged flow field for
January 1978, which has zonal variations that are qualitatively quite similar
to those of the average winter field(shown in Fig.
1)
in the upper troposphere.
The streamfunction fields for the basic state are shown in Fig.
1
of Frederik-
sen and Pun
(
1985). The forcing functions mentioned above are chosen in
such a way that, in the absence of drag and diffusion, the flow field for
January 1978 is an
exact
steady-state solution of the equations of motion.
However, if the basic state is perturbed, the perturbation will extract energy
from it and grow.
For the small-amplitude perturbation to the basic state, the fastest growing
linear instability mode for the January 1978 basic state obtained from a
three-dimensional instability calculation in a quasi-geostrophic model (Fre-
deriksen, 1983a) is used. The disturbance amplitude was chosen to
be
suffi-
ciently large,
so
that time-stepping errors are comparatively small, but small
enough
so
that the different interesting stages of evolution can be studied.
The disturbance kinetic energy per unit mass is
6.03
X
m2 sec2, and
the disturbance streamfunction at
a
=
0.7 is shown in Fig. 7. We see that the
disturbance is a monopole cyclogenesis mode with largest amplitudes in the
storm tracks in the Atlantic and Pacific Oceans. That is, it is similar to Mode
1
of
Case
1
in Fig. 2, but
is
somewhat more localized.
The model was integrated for a
period
of
10
days from the perturbed initial
conditions and the evolution of the disturbance was examined. Here the

INSTABILITY THEORY AND NONLINEAR EVOLUTION
293
FIG.
7.
Disturbance streamfunction at
u
=
0.7
used to perturb basic state in primitive-equa-
tion model.
disturbance at a given time is the difference between the flow field at a given
time and the basic January 1978 flow, which (in the absence of time-stepping
errors and drag and diffusion) would remain constant with the specified
forcings.
4.2.
Disturbance Kinetic Energy Spectra
The developments of the disturbance kinetic energy zonal wavenumber
rn
spectra are shown in Fig.
8
for the 10-day period. We see that there is a
gradual and continual change in the energy spectra, until by day
10
the
disturbance energy preferentially populates the larger scales. In fact, errors
