Saltzman B. (editor) Anomalous Atmospheric Flows and Blocking

Подождите немного. Документ загружается.

WIN-NIELSEN

published before

1940.

not know ifthis

story

is true, but it is nevertheless

a fact that for our present problems at the workshop there is little to

gain

the very old literature.

Let me try to give an eye-witness account of these early developments. It

follows that such an account necessarily

will

be somewhat personal, but I

shall naturally try to cover the main events. We may conveniently take our

starting point in the upper-air network which was created during and imme-

diately after World War

11.

was

considered by some forward-looking

meteorologists, primarily Bjerknes and Mintz at the University of Califor-

nia,

Los

Angeles and

Starr

and

his

colleagues at the Massachusetts Insti-

tute of Technology, that this network was good enough to study the general

aspects

of the atmospheric circulation. The first attack was on the primary

quantities such

meridional cross-sections of the zonally averaged wind

and temperature fields, but at the same time there were calculations of the

meridional transport of momentum and specific heat. The main question at

that time, approximately

1950,

was to determine the relative role of the

mean meridional circulation and the transport of the eddies. Particularly,

the MIT school under the leadership of

Starr

came out very strongly in

favor of the important role of the transient eddies in accomplishing the

necessary transport

both momentum and heat.

rather strong reaction to their somewhat overstated

case

came particu-

larly from

Palmen of Finland, who argued convincingly that the mean

meridional circulation was still of great importance in the tropics as com-

pared to the eddies.

lively discussion developed both at scientific confer-

ences and in the literature, but it

was

difficult to settle the disagreements

because the network was not

good

enough

calculate the mean meridional

circulations with sufficient accuracy.

very important theoretical development took place with Lorenz’s

955)

formulation of the concept

available potential energy and his

description of the atmospheric energy cycle, resulting in the famous four-box

energy diagram in which both available potential energy and kinetic energy

were divided into the energy contained in the zonally averaged fields and that

contained in the eddies. Many followers of Lorenz, including the speaker,

used many investigations to calculate the various generations, conversions,

and dissipations.

It has of course been known for many years that the radiation from the sun

drives the atmosphere, and that the kinetic energy ultimately is dissipated,

i.e., turned back to heat, by the forces of friction in the atmosphere. Lorenz’s

(1955)

major contribution concerning atmospheric energetics was to show

that the sum of potential and internal energy is at a minimum when the

isentropic and the isobaric surfaces coincide with the horizontal surfaces.

GLOBAL SCALE CIRCULATIONS-A REVIEW

Internal and potential energy which are proportional in an integrated sense

in a hydrostatic atmosphere are

generated,

according to Lorenz’s theory,

when on average the warm air masses are heated and the cold air masses are

cooled. On the other hand, the kinetic energy in the atmosphere is main-

tained by an internal process whereby internal and potential energy are

converted

into kinetic energy. Such a

conversion

will take place when on

average warm air masses are rising and cold air masses are sinking. When

such a process takes place it is seen that the center of gravity for the atmo-

sphere is lowered, thus giving less potential energy. Finally, the kinetic en-

ergy is turned back into heat by the work of the frictional force, i.e., kinetic

energy is dissipated.

The “easy” quantities were the conversions from zonal to eddy energies

for both available potential energy and kinetic energy, because the main part

of these could be computed from the temperature field and the horizontal

wind field, and because the already mentioned meridional transports of

sensible heat and momentum by the eddies were important elements of these

calculations.

Much more difficult were the calculations of the generations of zonal and

eddy

available potential energies because they depend on a knowledge of the

so-called diabatic heating of the atmosphere. Equally difficult were the con-

versions between available potential energies and kinetic energies in both

zonal and eddy form because they require a knowledge of the vertical ve-

locity.

We (Wiin-Nielsen and Brown, 1960) attempted to calculate the genera-

tions of available potential energy by first calculating the heating field as a

residual from the thermodynamic equation every 12 hr, then proceeding to

the calculations of the generations. This work was later carried further by

Brown

(

1964).

Our work became immediately quite controversial because while the total

generation

G(A)

and the zonal generation

G(A,)

were positive, it turned out

that the eddy generation

G(AE)

was negative. We could of course argue that

the negative generation indicated that on the average the cold air masses

were warmed and the

warm

air masses were cooled, and that this indeed was

the case in the radiation and in the exchanges between the atmosphere and

the underlying surface whether it

was

continents, ice

snow fields, or the

oceans. On the other hand, when it came to the heat from condensation and

evaporation processes, all we could

say

was that the former processes gave a

larger contribution than the latter.

In these years there was also an important contribution by

Barry

Saltzman

(1957), who formulated the energy relations in the spectral domain. His

formulation was still based on a Fourier transformation along individual

WIIN-NIELSEN

latitude circles, but the normal field representation in the meridional and

vertical directions. We had not yet moved completely into the spectral do-

main in 1957. Both Saltzman and

were independently engaged in the

special aspects of the energy conversions from eddy available potential en-

ergy to eddy kinetic energy.

used the vertical velocities as they were com-

puted from a two-level, quasi-geostrophic model at use at the Joint Numeri-

cal Weather Prediction where

was employed, and Saltzman and Fleisher

used a similar although not identical procedure.

The main result was a spectrum with a marked maximum corresponding

to the scale of baroclinic instability, and another maximum for the very long

waves. It was difficult to explain the second maximum, but it was demon-

strated that mountains and heating could reduce it if they had been incorpo-

rated

the model used at the time.

The time series used for these early calculations were pitifully short, and

the results could not

considered

more than snapshots of the general

circulation. It became quite a task during the coming years to extend all the

calculations into the spectral domain and to cover a time period of at least a

year.

had the opportunity to do this during my time at the National Center

for Atmospheric Research (NCAR) and later at the University of Michigan.

The calculations

the energetics were extended by distinguishing between

the baroclinic and barotropic components of the kinetic energy, corre-

sponding to the kinetic energy of the deviations from the vertical mean flow

and the kinetic energy of the mean flow itself.

had the opportunity to

develop this concept from a theoretical as well

an observational point

view in some early papers

(

Wiin-Nielsen, 1962). For the concept itself

was

certainly inspired by

Smagorinsky

(

1963), who later used it in his analysis

the so-called basic experiment with his general circulation model.

am now approaching the subject of this workshop, i.e., the anomalous

circulation in the atmosphere. My co-workers, Margaret Drake and John

Brown, Jr., and

964) had decided that we would use the year 1962

representative year for calculations of the energetics in the spectral domain.

We started from January 1962 and

did

the calculations day by day, making

monthly averages

we went along. The results looked absolutely normal for

the larger part

1962 in the sense that the directions

the energy genera-

tions, conversions, and dissipations agreed with the now classical picture,

i.e.,

C(A,,

AE)

and

C(KE,

K,)

were positive.

we were about to finish the

year and looked at the average results

for

December 1962, we were aston-

ished to find that

C(K,,

K,)

was negative, i.e., the eddies received kinetic

energy from the zonal flow. Our first reaction was that something had gone

wrong with the data, obtained from the National Meteorological Center

(NMC) on magnetic tapes, or some silly mistake had come into the program

GLOBAL SCALE CIRCULATIONS-A

REVIEW

used for the calculations. Checking and rechecking confirmed that every-

thing was in order and we had to conclude that we were dealing with an

anomalous situation.

We decided then out of curiosity that it would be interesting to continue

the calculations into

1963,

and we completed the first few months of that

year with the results that

C(KE,

K,)

stayed negative well into March

1963.

It was thus discovered from energy calculations that it is entirely possible

for the atmosphere to work in at least two quite different modes. Also this

result was, of course, controversial, and the reaction was almost immediate

from MIT. Professor

Stan

questioned our results due to the fact that our

formulations were different from his, because

C(KE,

K,)

can be formulated

in two different ways, depending on an integration, by parts. The question

came up because we used a less than hemispheric domain, and it was there-

fore a question of boundary conditions. John

Brown, Jr., who was a

graduate of MIT, was put on the problem, and he was able to show that

although the two formulations gave different results because ofthe boundary

conditions, it was definitely not enough to reverse the sign of

C(KE,

K,),

which stayed negative.

Our calculations were of course not done in real time, but we were not far

behind

you can see from the publication dates. When it was possible

,somewhat later to look at the real circulation during these anomalous winter

months, it became clear that the winter

1962/1963

was indeed very far from

normal. The upper air maps show rather typical blocking situations. All

kinds of weather records were broken during the period, depending on where

a given locality

was

situated with respect to the very longest waves in the

upper air flow. Both the spectra of available potential energy and of kinetic

energy showed that the greater portion of the energies were in the very

longest waves.

Our conclusion must therefore be that it is possible for the atmosphere

work in at least two separate regimes. One of these dominates most of the

time. It is characterized by a typical baroclinic regime in which the scale,

characteristic of baroclinic instability, is at work more or less continuously

giving rise to positive values of

C(A,,

AE)

and

C(K,,

K,).

The other regime

is in a sense more barotropic because

C(KE,

K,)

is negative

it would be

during instability of the barotropic kind. In any case, the larger scales domi-

nate, containing most of the energy, the flow is quite anomalous, and it is of

blocking nature.

My own engagement in observational studies of atmospheric energetics

came more or less to an end in

1967,

when I wrote a summary paper on the

annual variation and spectral distribution of energy in the atmosphere. I

discovered the third power law for the distribution of kinetic energy in the

WIN-MELSEN

atmosphere for relatively

high

wave numbers. Since then this work has been

continued by

her,

Steinberg,

Barros, and above all by M. Chen, who

still continues to contribute to the study of atmospheric energetics.

THE NEAR

PAST

Most meteorologists

agree,

probably, that the present intense interest in

anomalous circulations, including blocking situations, stems from recent

theoretical papers written some

years

ago.

It is of course true that the

forecasters, especially those engaged in the longer ranges, have been aware of

very anomalous circulations for a long time. In this regard, we may recall the

investigations of blocking

carried

out by Rex from a synoptic and statistical

point of view. The more recent studies by Austin

(1980)

in the United

Kingdom, along the same lines and forming

natural extension of Rex’s

work

(

1950),

are a welcome addition.

understand that further observational

studies

will

be presented at this workshop, and

am looking forward to them.

The theoretical studies started with Charney and DeVore

(1979)

and

Wiin-Nielsen

(

1979),

who independently showed that a low-order, nonlin-

ear barotropic system, with forcing and dissipation for certain parameter

values, may

possess

multiple steady states, of which several may

stable.

The bifurcation depends on the strength of the forcing, and both investiga-

tions suggest that the blocking phenomenon may indeed be one such stable

state. In more detail, one finds typically

two

stable steady states, of which one

has

a rather strong zonal current

(high

index) and relatively small amplitudes

in the eddies, while the other has a much weaker

zonal

current (low index)

and a larger amplitude of the waves (the blocking situation).

My own interest in such problems started in the early

1970s

because ofthe

catastrophe theories developed by the French mathematician Thom, and

because

got interested in certain aspects of population dynamics

camed

out by ecologists who have developed relatively simple, but still nonlinear

models of natural or laboratory situations of

two

or more competing popula-

tions. In my writings on the subject you

will

find some examples selected

from these

fields.

The most recent simple example from the meteorological field which

displays the properties of multiple steady states is probably the spectral form

of the advective equation with or without forcing and dissipation:

aupt

u(du/dx)

--EU

B(U~

(1)

Using an expansion of

and

in trigonometric series and reducing the

in which

is the velocity in the x-direction,

time, and

forcing.

GLOBAL SCALE CIRCULATIONS-A

REVIEW

spectral equations to just two components, we find, with the proper scaling,

Considering the case

0 we find that the steady states have either

The steady states are therefore

(0,

YE); ((YE

l)ln,

(-(YE

l)”’,

We note that only one steady state exists for

while three exist for

The perturbation equations for a given steady state are obtained in

the usual way. They are (with primes indicating perturbation quantities)

dx’ldt

XY‘

YX’

X‘

dy’ldt

~XX’

y’

(3)

from which we seek solutions of the form

(x’,

y’)

(x;, y;)x

em.

The fre-

quency equation is:

(a+

l)*-y(o+

1)+2x2=0

(4)

Considering first the steady state

(0,

yE),

we find that

and

indicating that

this

steady state is stable when it exists alone

(yE

l),

while

it becomes unstable when the other two steady states exist. For these steady

states

(+(yE

we find that

l/2(-

k(9

8yE)’/’)

when

The solution turns out to indicate stability for

all

permissible values OfyE.

The only difference is that for

918

we have negative values of

while for

918,

is complex with a negative real value.

We may thus conclude from this analysis that the nature of the steady state

depends entirely on the magnitude of the forcing. For

there is only

one steady state which is stable. For

there are three steady states of

which the two new steady states are stable, while the former single steady

state has become unstable.

may also be noted that the single steady state

which exists for

has small amplitudes, while the two steady states for

may have very large amplitudes for large values of

yE.

Finally, the

selected steady state depends on the initial condition.

The analysis described above was carried out in

1976

and is published in

the proceeding

the first European Centre for Medium Range Weather

Forecasts (ECMWF) seminar

(

Wiin-Nielsen,

1976).

Further extensions of

the analysis to more complicated systems of the same kind have been made

by Ullen and Win-Nielsen

(1980),

and Wiin-Nielsen

(1982, 1983).

We shall now proceed to other systems. Most investigations so far have

been of low-order, nonlinear systems based on the barotropic vorticity equa-

tion with forcing and dissipation. This is true also for the pioneering studies

WIIN-NIELSEN

of Charney and DeVore

979) and Wiin-Nielsen (1979). These studies

normally include a zonal component and one or more wave components.

The forcing may

classified

vorticity forcing and/or mountain forcing,

where the vorticity forcing, in my opinion, is a simulation of heating.

discussion has developed on whether or not both kinds of forcing are neces-

sary

to obtain multiple steady states. It is, however, quite clear by now that

they supplement each other, but multiple steady states may exist if only one

kind of forcing is present.

much more important question is related to how realistic these investi-

gations are. For the time being we shall discuss the solutions and leave the

question of how realistic low-order models are to

answered later. Several

serious questions can

raised

with respect to the realism of the solutions.

We note, for example, that

(1)

to bifurcate, i.e., to create multiple steady

states when a zonal component is included, rather large values of the ampli-

tude of the mountain and heating components are needed in the models

mentioned above;

(2)

the energy levels of the solutions produced by most

investigators are much higher than those obtained in observational studies;

(3)

correspondingly, generations, conversions, and dissipations are higher

than observational studies show that they should be.

decided about a year ago

(

Wiin-Nielsen, 1984) to investigate these ques-

tions in detail for the simple reason that my own studies are suspect in this

regard. For this purpose

used a model with the spherical components

(0,

(1,

n,),

and (1,

n2).

a general result it turned out that the energy

levels are quite sensitive to the meridional scales involved, i.e.,

and

n2,

in the sense that the smaller the scale, the smaller the energy amounts.

Concerning the energies, it turns out that the steady state energies can be

expressed in

and

which are the amplitudes ofthe components

(0,

and

(0,

n).

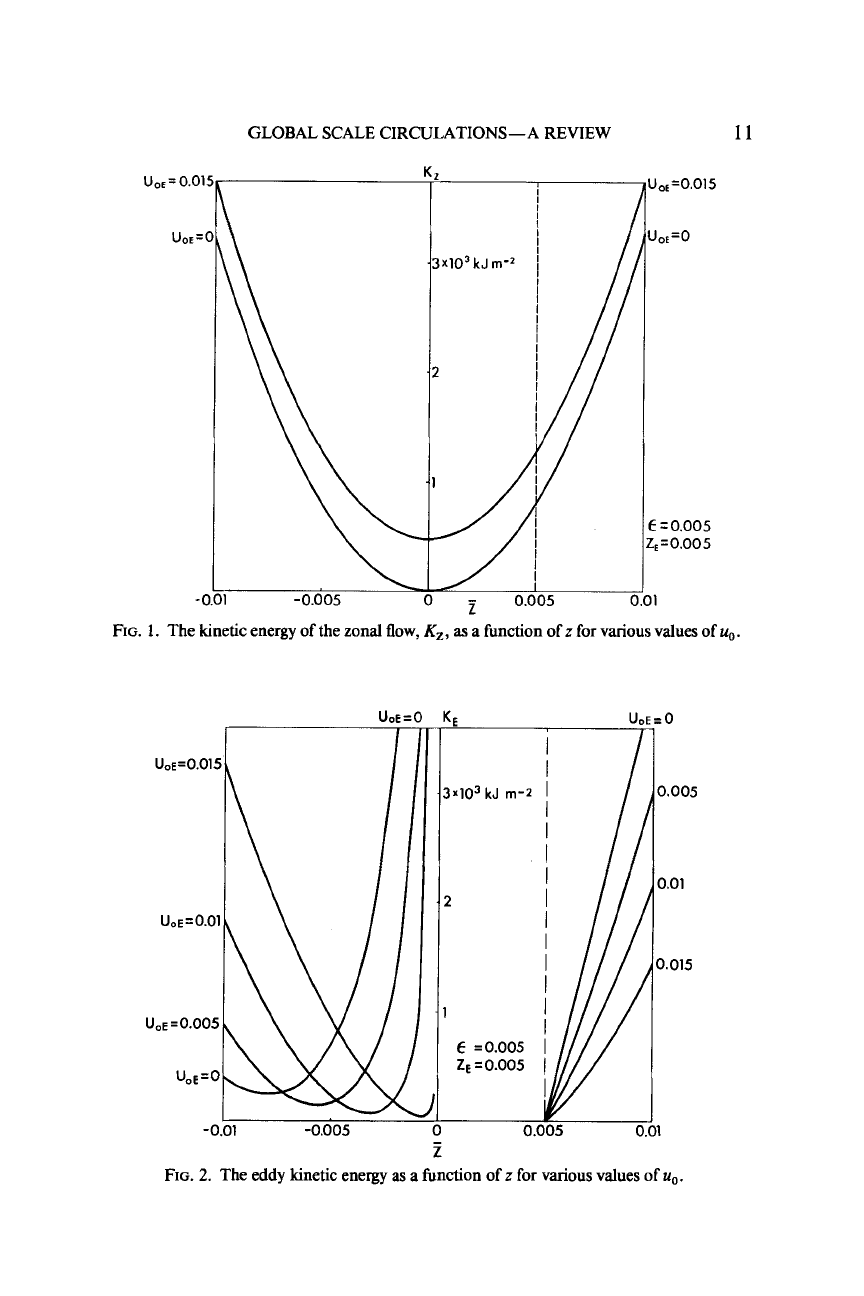
Figure

shows the zonal kinetic energy

a function of

for

various values of

uo.

It is seen that only small values

are permissible if&

shall have a reasonable value. Figure

shows, on the other hand, the eddy

kinetic energy

a function of the same parameters. For

it is seen

that

is an increasing function of

while distinct minima exist for

the energy values of

shall

reasonable, it is a question to have

around

the minimum for the given value of

uo.

These considerations indicate the

ranges for which reasonable solutions can

found.

can be seen, it is a

tight squeeze without much margin. It is nevertheless possible to find triple

solutions. The energetics of such stable solutions are shown in Fig.

Even if it is possible

shown above to obtain reasonable answers, it is

nevertheless a fact that the “window” in parameter space for proper solu-

tions is quite narrow. One may therefore question if these models, which are

strongly dependent on the zonal current, describe the true mechanism in

the atmosphere. Considering the synoptic development leading to blocking

UOE=

0.01

UOE=

GLOBAL SCALE CIRCULATIONS-A

REVIEW

U0,=0.015

uo,=o

0.005

zO.00 5

FIG.

The kinetic energy of the zonal

flow,

K,,

function

for

various

values

uo.

UoE:

-0.005

3x103

m-2

0.005

0.01

0.015

FIG.

2. The

eddy

kinetic energy

function of

for various values

A. C.

WIN-NIELSEN

0.32

0.19

0.69

0.560.87

+LJ-Ll+m

10.13 t0.13

10.07

0.68

56.0

0.81

0.31

20.1

4-3!44-9

0.13

8.4 0.20

FIG.

The energy

diagram

for stable solutions.

rather unlikely that a critical value of the zonal current is the decisive

factor. Rather, the impression

that the blocking configuration is the dying

ground of a set of traveling disturbances, and that it is maintained by them.

In discussions with

Sutera some months ago it occurred to us that the

block as a nonlinear yet global phenomenon perhaps depended on a wave

wave interaction rather than interaction between waves and the zonal cur-

rent.

a preliminary contribution to the solution of this problem

have

investigated the nonlinear aspects of wave- wave interaction with a view

toward multiple steady states and bifurcation. The starting point is also in

this

case

the barotropic vorticity equation with mountain and vorticity forc-

ing.

Using the scaling

a2R

for the streamfunction

radius of the earth,

angular velocity),

i2-l

the time scaling, and

RTo/g

as the

mountain scaling, we get the following nondimensional equation:

av2v/at

J(V~W,

I,V)

A,J(~,

2(av/a4

r(W

w*)

(5)

Following Platzman

(1962)

and using his notation we have the following

spectral equation:

where

K(y,

/I,

is the interaction coefficient and

n(n

I).

now possible to use the selection rules to reduce

Eq.

(6)

to three

complex equations for a triplet. If we further neglect the

term we may get a

closed system of three equations by assuming that only the imaginary parts

GLOBAL SCALE CIRCULATIONS- A

REVIEW

of the amplitudes are nonzero. The system then becomes

where

The simplifications leading to

Eq.

(7)

are

quite drastic, and the results should

viewed with some caution. At a later time

hope to report on the results

obtained without the neglect of the

effect and considering the complete

waves.

The energy relations for this system are easy to obtain. They

are

given

schematically in Fig.

in which we notice that they consist of

(i) generations of the form:

ciyiy,*

(ii) dissipation of the form:

ciy:

(iii) nonlinear interactions:

(Cj

cj)Kyly2y3

(iv) mountain effects:

A,K(m,yjyk

mkyj

yi)

We notice in this regard that the sums of the nonlinear interaction terms and

the mountain effects each are zero, indicating that they do not change the

total energy, but are distributive terms.

For purposes of illustration we shall

look

at an example. The following

components are selected:

(1,

3),

(2,2),

(3,4). The energy diagram is shown in

Fig.

in which the amounts of energy are given in the units

m-2,

while

generations, conversions, and dissipations are shown in

102

W m-2. Three

steady states have been found, and it can

shown that (a) and (c) are stable,

while (b) is unstable. Comparing

(a)

and (c) we notice first of

all

that they

differ

greatly

in the energy distribution,

because

(a) has most ofthe energy on

component

(1)

while

(c)

has a maximum on component

(2).

In addition,

component

(1)

has the largest generation in

case

(a), while component

(2)

takes

over this role in case (c). It should also

mentioned that the mountain

heights

used

this

example were taken

those components which were