Russ J.C. Image Analysis of Food Microstructure

Подождите немного. Документ загружается.

(a)

(b)

FIGURE 3.34 Measurement of orientation: (a) SEM image of egg shell membrane (courtesy

of JoAnna Tharrington, North Carolina State University, Food Science Department); (b)

application of the Sobel direction operator; (c) histogram of image (b), showing the relative

frequency of orientations from 0 to 360 degrees; (d) data from (c) replotted as a rose of

orientations (radius represents frequency).

2241_C03.fm Page 165 Thursday, April 28, 2005 10:28 AM

(a)

(b)

(c)

FIGURE 3.35 Measuring orientation: (a) image of collagen ﬁbers; (b) application of Sobel

orientation ﬁlter; (c) histograms of the orientation data (left, conventional 0.255 grey scale

range corresponds to 0. 360 degrees; right, same data plotted as a rose plot) showing preferred

orientation of the ﬁbers.

2241_C03.fm Page 166 Thursday, April 28, 2005 10:28 AM

Thresholding of regions in an image can be illustrated by using one of the

Brodatz textures from Figure 3.28. The herringbone fabric pattern shown in Figure

3.38 is constructed with ﬁbers running vertically and horizontally, but the visual

impression is one of diagonal stripes. Applying the Sobel orientation ﬁlter assigns

grey scale values to each pixel, which in this example has been reduced to a 0 to

(a) (b)

(e)

FIGURE 3.36 Orientation measurement for separated cellulose ﬁbers: (a) original; (b) ori-

entation value assigned to pixels; (c) mask produced by thresholding the ﬁber image; (d)

elimination of all non-ﬁber pixels (note that the presence of two orientation values, different

by 128 grey scale values or 180 degrees, on opposite sides of each ﬁber is particularly evident

in this image); (e) rose plot of histogram showing preferentially oriented ﬁbers.

2241_C03.fm Page 167 Thursday, April 28, 2005 10:28 AM

FIGURE 3.37 Assigning hue colors to the ﬁber angles (see color insert following page 150).

(a) (b)

FIGURE 3.38 Example of directional thresholding: (a) original Brodatz herringbone pattern;

(b) Sobel orientation; (c) noise reduction; (d) overlay of ﬁnal thresholded result on original image.

2241_C03.fm Page 168 Thursday, April 28, 2005 10:28 AM

180 degree range instead of the usual 0 to 360 degrees. Applying a median ﬁlter

reduces the noise due to local random variations, and produces an image with two

predominant brightness values, which correspond to the areas containing the two

diagonal patterns. When automatically converted to a binary image as described in

the section on thresholding, these can be measured to determine the dimensions,

etc., of the regions.

FINDING FEATURES IN IMAGES

The herringbone textile pattern in the preceding ﬁgure is a good example of an

image containing many repetitions of the same structure. While each individual

chevron is slightly different from all of the others, due to the individualities of the

ﬁbers and the random noise in the image, the underlying structure is the same. By

averaging together all of the repetitions, a much better image can be obtained of

that structure. This is most easily accomplished by using the Fourier transform. The

spikes of high amplitude in the power spectrum indicate the predominant frequencies

and orientations of the terms that combine to produce the image of the repetitive

structure. In the examples of removal of periodic noise in the preceding chapter,

ﬁnding these spikes and eliminating those terms was used as a way to remove the

periodic noise and keep the rest of the image. Now we will do the opposite: keep the

periodic (structural) signal and remove the random superimposed variability and noise.

The power spectrum can be processed like any other image to locate the spikes

and produce a ﬁlter that will keep them and remove other frequencies. In many cases

the top hat ﬁlter is a good tool for locating the spikes, or points of high amplitude.

In this particular example (Figure 3.39) it is more efﬁcient to remove the spikes by

using a rank ﬁlter to perform a grey level erosion (replace every pixel with its

brightest neighbor) in order to generate a background which is then subtracted from

the original. The resulting ﬁlter or mask is shown in the ﬁgure. Removal of all the

frequencies and orientations that are white in the ﬁlter, and keeping those where the

ﬁlter is black, allows performing the inverse Fourier transform to obtain an image

in which all of the repetitions of the basic chevron structure have been averaged

together, to produce a low noise average.

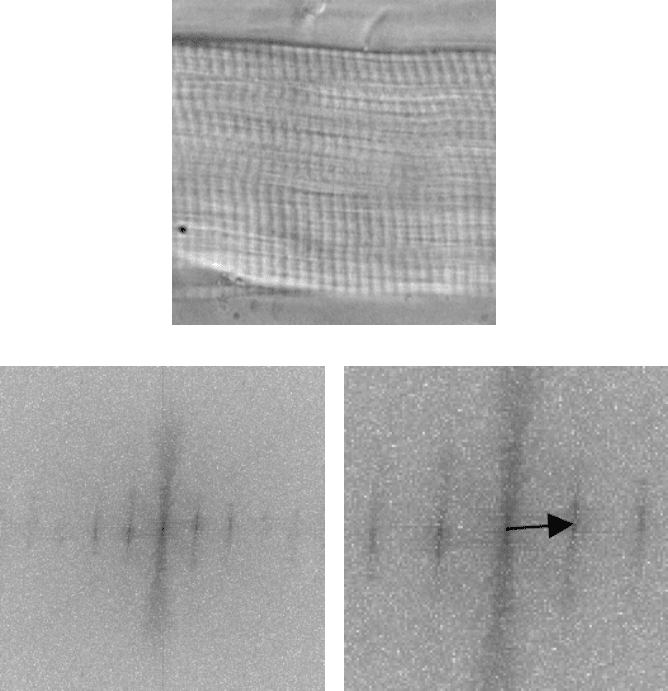
The Fourier power spectrum also provides a useful summary of all the periodic

information in the original image that can be used for measurement. The z-bands

in the muscle tissue shown in Figure 3.40 are regularly spaced but awkward to

measure. In order to obtain good precision, many separate locations would have to

be measured and the results averaged. The Fourier transform provides averaging for

the entire image automatically. The distance from the center to the ﬁrst spike in the

power spectrum gives the frequency (and the orientation) of the fundamental peri-

odicity that is present. The spacing can then be calculated as the width of the original

image divided by that radial distance.

Many images contain multiple repetitions of the same structure, but they are not

regularly spaced and, hence, are not represented by simple spikes in the Fourier

transform power spectrum. Nevertheless, it may be possible to efﬁciently ﬁnd them

by using the frequency-space representation of the image. However, an initial under-

standing of the method is probably easiest using the familiar pixel version of the

2241_C03.fm Page 169 Thursday, April 28, 2005 10:28 AM

image. Imagine isolating a single representative example of the structure of interest,

placing it on a transparent overlay, and sliding it to all possible positions on the

original image looking for a match. As a measure of how well the target image is

matched by the underlying data, the individual pixel values in the neighborhood are

rotated 180 degrees, multiplied together, and summed. This cross-correlation value

rises to a maximum when the target is located. It turns out that the arithmetic

procedure, which must be applied with the target centered at every pixel in the

original image, can be carried out very quickly and straightforwardly using the

Fourier transform.

For those interested in the underlying math, the Fourier transforms of the target

and the original image are both computed. These are then multiplied together, but

the values are complex (real and imaginary) and for cross-correlation the phase angle

(a)

(b) (c)

FIGURE 3.39 Example of averaging in Fourier space: (a) Fourier transform power spectrum

of the original image from Figure 3.38; (b) mask created to keep just the spikes (high amplitude

terms); (c) inverse transform of just the high amplitude terms producing an averaged image.

2241_C03.fm Page 170 Thursday, April 28, 2005 10:28 AM

of the target values are rotated by 180 degrees. Instead of requiring many multipli-

cations for each pixel location, there is just one multiplication for each pixel. Then

an inverse Fourier transform is applied to the resulting data, producing an image in

which dark spots correspond to the locations where the target was matched (and the

darkness of the spot is a measure of how well it was matched).

In the example in Figure 3.41, blisters on packaging are difﬁcult to see visually

(or count automatically) because they do not have simple contrast (they are bright

on one side, dark on the other), and because the image is rather noisy. Selecting one

of the blisters as a representative target and performing cross-correlation with the

entire image marks all of the blisters for easy recognition and counting. Notice that

(a)

(b) (c)

FIGURE 3.40 Measuring regular spacings: (a) original image of z-bands in muscle tissue;

(b) Fourier power spectrum; (c) enlargement of the central portion of (b), showing the radial

distance to the ﬁrst spike. The average spacing in the original image is equal to the width of

that image (256 pixels) divided by the radial distance (26.5 pixels) = 9.6 pixels. Of course,

this must be used with the original image magniﬁcation to calculate the actual spacing.

2241_C03.fm Page 171 Thursday, April 28, 2005 10:28 AM

the sizes of the blisters vary by about a factor of 2, and so the target does not perfectly

match all of the occurrences, but the marks are still dark enough to locate them all.

Cross-correlation can also see through clutter, noise, and the presence of other

shapes to locate features. In the example in Figure 3.42, latex spheres have been

(a)

(b)

FIGURE 3.41 Surface image of packaging showing blisters: (a) the one in the center of the

ﬁeld (marked with a white arrow) was selected as the target. The cross-correlation result

(b) marks the location of all of the blisters present for easy counting.

2241_C03.fm Page 172 Thursday, April 28, 2005 10:28 AM

collected from a ﬂuid onto Nuclepore ﬁlters. The holes in the ﬁlter and the presence

of other dirt on the ﬁlter make it difﬁcult to count the particles, as does the varying

contrast (isolated spheres have greater contrast than ones in groups). Because of the

noise in the image, and the desire to apply the processing automatically to literally

thousands of images, a target image was constructed by averaging together (manu-

ally) the images of about a dozen individual spheres from multiple original images.

An enlarged copy of the target is shown in Figure 3.42(a).

Cross-correlation with this target marks all of the spheres. To simplify counting,

a top-hat ﬁlter was applied to the cross-correlation result to locate all of the signif-

icant marks. This produced uniform black marks for counting. This image can then

(a) (b)

FIGURE 3.42 Nuclepore ﬁlter with latex spheres: (a) original SEM image with superimposed,

enlarged target image as discussed in text; (b) cross-correlation result; (c) application of top-hat

ﬁlter (inner radius = 4 pixels, outer radius = 6 pixels, crown height = 12 grey levels) and the

resulting count of the number of particles present; d) convolution with the target image shows

just the particles without the background or other features present in the original image.

2241_C03.fm Page 173 Thursday, April 28, 2005 10:28 AM

(a)

(b)

FIGURE 3.43 Image of the surface of a particulate whey protein isolate gel network (a)

(courtesy of Allen Foegeding, North Carolina State University, Department of Food Science).

The autocorrelation result (b) provides a measure of the average size and shape of the

structuring element (shown by thresholding a contour line on the dark spot).

2241_C03.fm Page 174 Thursday, April 28, 2005 10:28 AM