Рубин А.Б., Пытьева Н.Ф., Ризниченко Г.Ю. Кинетика биологических процессов

Подождите немного. Документ загружается.

Корни

%i,

действительны

одного

знака

Тогда коэффициенты преобразования действительны, и мы име-

ем переход от действительной плоскости х, у к действительной,

плоскости |, г].

Разделив одно из канонических уравнений

(1.4—7)

на

другое,

получим

dr\ _

Интегрируя это уравнение, находим

где а =

(1.4-9)

(1.4—10)

Условимся понимать под Яг корень характеристического урав-

нения

с большим модулем (это не нарушает общности нашего рас-

смотрения).

Тогда, поскольку в рассматриваемом

случае

Ки h

одного знака, а>1 и мы имеем дело с интегральными кривыми

параболического типа.

Все интегральные кривые (кроме оси ц, которой

соответствует

с = ос) касаются в начале координат оси |, также интегральной

кривой

уравнения (1.4—13). Нача-

ло координат является особой точ-

кой.

Выясним

теперь направление

движений на фазовой плоскости.

Если

A.2 отрицательны, то, как

видно из уравнений (1.4—7), |||,

|т)|

убывают

с течением времени.

Изображающая точка приближает-

ся

к началу координат, никогда, од-

нако,

не достигая его в конечное

время,

так как это противоречило

бы теореме

Коши,

которая

утверж-

дает,

что через

каждую

точку фа-

зовой плоскости проходит лишь од-

на

фазовая траектория системы

уравнений (1.4—7). Такая особая точка, через которую проходят

интегральные кривые подобно

тому,

как семейство парабол

г/=сх

(а>0) проходит через начало координат, носит название

узла

(рис.

1.12).

Нетрудно видеть, что сбстояние равновесия, соответствующее

узлу,

при к\,

Хг<0

является устойчивым по Ляпунову, так как

изображающая точка по всем интегральным кривым движется по

направлению к началу координат. Устойчивое состояние равнове-

сия,

которое

соответствует

особой точке типа

узла,

называется

устойчивым узлом. Если же Ки Я,2 положительны, то |£| и |т]| воз-

растают с течением времени и изображающая точка с течением

Рис.

1.12.

Особая

точка

типа

узел

на

плоскости

канонических

коор-

динат

|, 11

времени удаляется от начала координат. В таком

случае

мы имеем

дело с неустойчивым узлом.

Вернемся теперь на фазовую плоскость х, у. Общий качествен-

ный

характер поведения интегральных кривых вокруг состояния

равновесия при этом не меняется, но касательные к интегральным

кривым

в особой точке уже не

будут

совпадать с осями координат.

Угол

наклона этих касательных к осям координат определяется

соотношением коэффициентов а, j3, Y> б в выражениях (1.4—8).

Рис.

1.13. Устойчивый (а) и неустойчивый (б) узел на

фазовой

плоско-

сти

х, у

Фазовые траектории вокруг устойчивого и неустойчивого

узла

на

фазовой

плоскости х, у, когда Л[ и Я

действительны и одинаковых

знаков,

представлены на рис. 1.13.

Следует

отметить, что для многих биологических систем яв-

ляется характерным «бесколебательный» переход из произволь-

ного начального состояния в стационарное состояние, характери-

стики

которого определяются внутренними свойствами самой си-

стемы. Такие системы описываются дифференциальными уравне-

ниями,

имеющими своим стационарным решением устойчивую осо-

бую точку типа узел. В IV части мы познакомимся подробно с

одной

из таких систем — системой транспорта электронов в про-

цессах первичных реакций фотосинтеза.

Корни

и }.2

действительны,

но

разных

знаков

Преобразование от координат х, у к координатам |, г\ опять

действительное. На плоскости |т] точно так же имеет место

кано-

ническая

система

A,rj,

(1.4-7)

однако теперь Xi и %% разных знаков. Уравнение кривых на фазо-

вой

плоскости имеет вид

—L

= — a-L,

гдеа

Интегрируя, находим

(1.4-11)

Это уравнение определяет семейство кривых гиперболического

типа, где обе оси координат—асимптоты (при а=

мы имели бы

семейство равнобочных гипербол). Оси координат и в этом

случае

являются интегральными кривыми; это

будут

единственные инте-

гральные кривые, проходящие через начало координат. Каждая из

них состоит из

трех

фазовых траекторий системы уравнений

(1.4—7): из

двух

движений к состоянию равновесия (или от со-

стояния

равновесия) и из состояния равновесия.

Начало координат является единственной особой точкой рас-

сматриваемого семейства интегральных кривых. Все же остальные

интегральные кривые

суть

гиперболы, не проходящие через начало

координат (рис.

1.14).

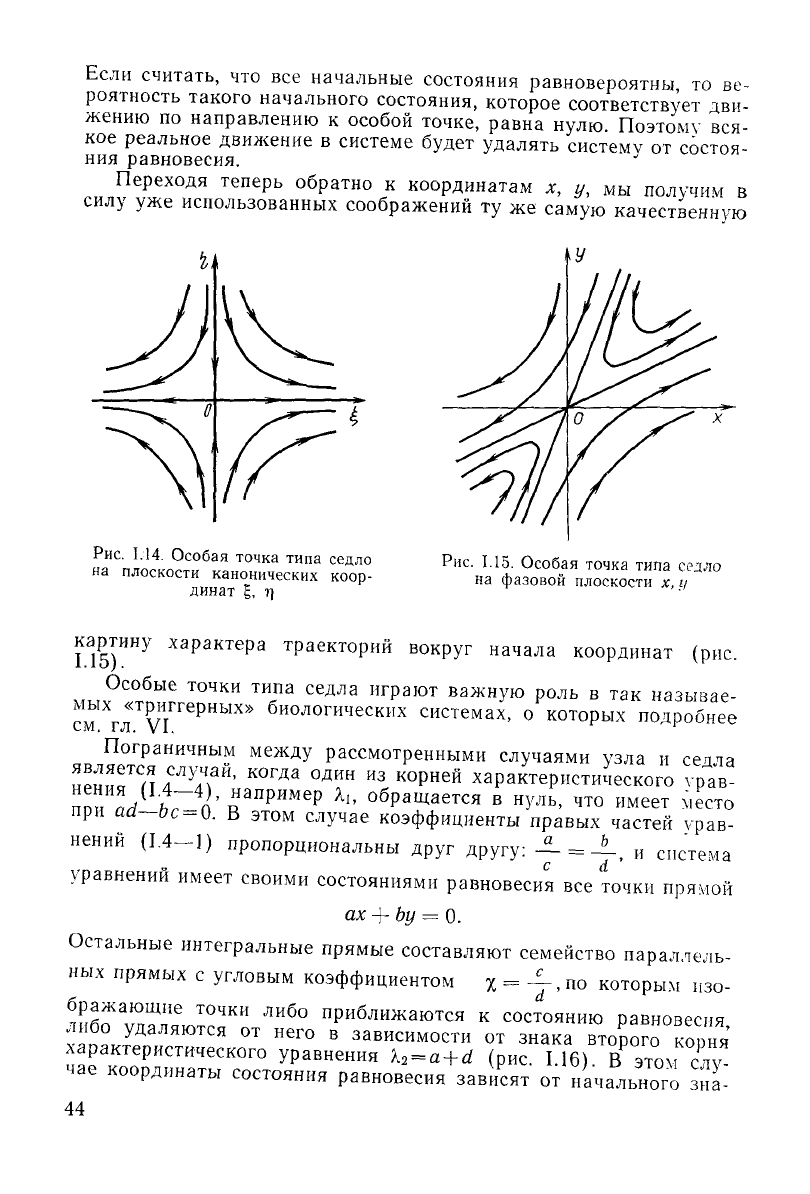
Такая особая точка называется особой точ-

кой

типа седла.

Рассмотрим характер движения изображающей точки по фазо-

вым траекториям вблизи состояния равновесия. Пусть, например,

/ч>0,

а Хг<0. Тогда изображающая точка, помещенная на оси %,,

будет

удаляться от начала координат, а помещенная на оси г| —•

будет

неограниченно приближаться к началу координат, не дости-

гая его в конечное время. Легко убедиться, что где бы ни нахо-

дилась изображающая точка в начальный момент (за исключе-

нием

особой точки и точек на асимптоте т] = 0), она всегда в ко-

нечном

счете

будет

удаляться от состояния равновесия. Даже в

том случае, если вначале представляющая точка движется по ка-

кой-либо

из интегральных кривых по направлению к особой точке,

конце концов она все же

уйдет

как угодно далеко от состояния

равновесия во

всех

случаях,

кроме движения по асимптоте г| = 0.

Следовательно, в рассматриваемом

случае

состояние равновесия

неустойчиво, ибо мы не можем выбрать область 6(е) так, чтобы

представляющая точка, находившаяся в начальный момент време-

ни

в этой области, не вышла в дальнейшем за пределы заданной

области е. Очевидно, что особая точка типа седла всегда неустой-

чива.

Лишь при движении по асимптоте т] = 0 система

будет

прибли-

жаться к состоянию равновесия. Однако этот специальный случай

движения к состоянию равновесия не нарушает утверждения о

том, что состояние равновесия в данном

случае

неустойчиво. Дей-

ствительно, при любых начальных условиях, отличающихся от тех

специально

выбранных, которые точно соответствуют асимптоте

4 = 0, система

будет

всегда удаляться от состояния равновесия.

Если

считать, что все начальные состояния равновероятны

то ве-

роятность такого начального состояния, которое соответствует дви-

жению по направлению

особой точке, равна нулю Поэтому вся-

кое

реальное движение

системе

будет

удалять систему

от

состоя-

ния

равновесия.

Переходя теперь обратно

координатам

х, у, мы

получим

силу уже использованных соображений

ту

же самую качественную

Рис.

1.14. Особая точка типа седло

на

плоскости канонических

коор-

динат

1, т)

Рис.

1.15. Особая точка типа седло

на

фазовой плоскости х,

картину характера траекторий вокруг начала координат

(рис.

Особые точки типа седла играют важную роль

так называе-

1Х

гл

<Т

у1

ГГерНЫХ>> биологических

системах,

которых подробнее

Пограничным

между

рассмотренными случаями

узла

седча

ZTn

аЙ

ГДа

ДИН И3

°Р

ней

характеристического урав-

пои

(

ьГп'«

аПрИМер

Хи

об

аи

ет

ся

нуль, что имеет место

при

ad—bc-0.

этом

случае

коэффициенты правых частей урав-

нений

(1.4—1)

пропорциональны

друг

другу:

- = 1

система

уравнений имеет своими состояниями равновесия все точки прямой

ах

by =

Остальные интегральные прямые составляют семейство параллель-

ных прямых

угловым коэффициентом

= ~,

по которым пзо-

ЙГ™я

ютГ

КИ

ЛИб

иб

™ются

состоянию равновесия,

либо удаляются

от

него

зависимости

от

знака второго

копня

характеристического уравнения k

= a + d (рис

16)

этом

чае координаты состояния равновесия зависят

от

начального

ченпя

переменных. Подобные прямые состояний равновесия пред-

ставляют собой стационарные решения некоторых моделей эколо-

гических систем (Свирежев, Елизаров, 1972).

Х\ и Х

комплексные

сопряженные

Нетрудно видеть, что в этом

случае

при действительных х и у

мы

будем

иметь комплексные сопряженные £ и т). Однако, вводя

еще одно промежуточное преобразование, можно и в этом

случае

свести рассмотрение к действительному линейному однородному

преобразованию. Положим

(1.4-13)

= пу — ibi, ц = и — до,

где а\, Ь] и и, v — действительные величины. Тогда можно пока-

зать, что преобразование от х, у к и, v является при наших пред-

положениях действительным, линейным, однородным с детерми-

нантом,

отличным от нуля. В силу уравнений

(1.4—7)

(1.4—13)

имеем

dt dt

откуда

dt dt

->••*•>-•"

dv . dv i ., . / .

—

l —- = (

i —

i) (« — iV),

du ,

~—

= a

u~b

(1.4—14)

a{u -f- Ь

и.

Разделив второе

из

уравнений (1.4—14)

на

первое, получим

уравнение

dv a

v -f-

biii

/т л

г,

du а^и — bjv

которое

легче

интегрируется после перехода к полярной системе

координат. В полярной системе г, ф после подстановки

dr а

и = г cos

Ф,

v = r sin ф получим = —— г,

dcp

откуда

г = Се~*.

(1.4—16)

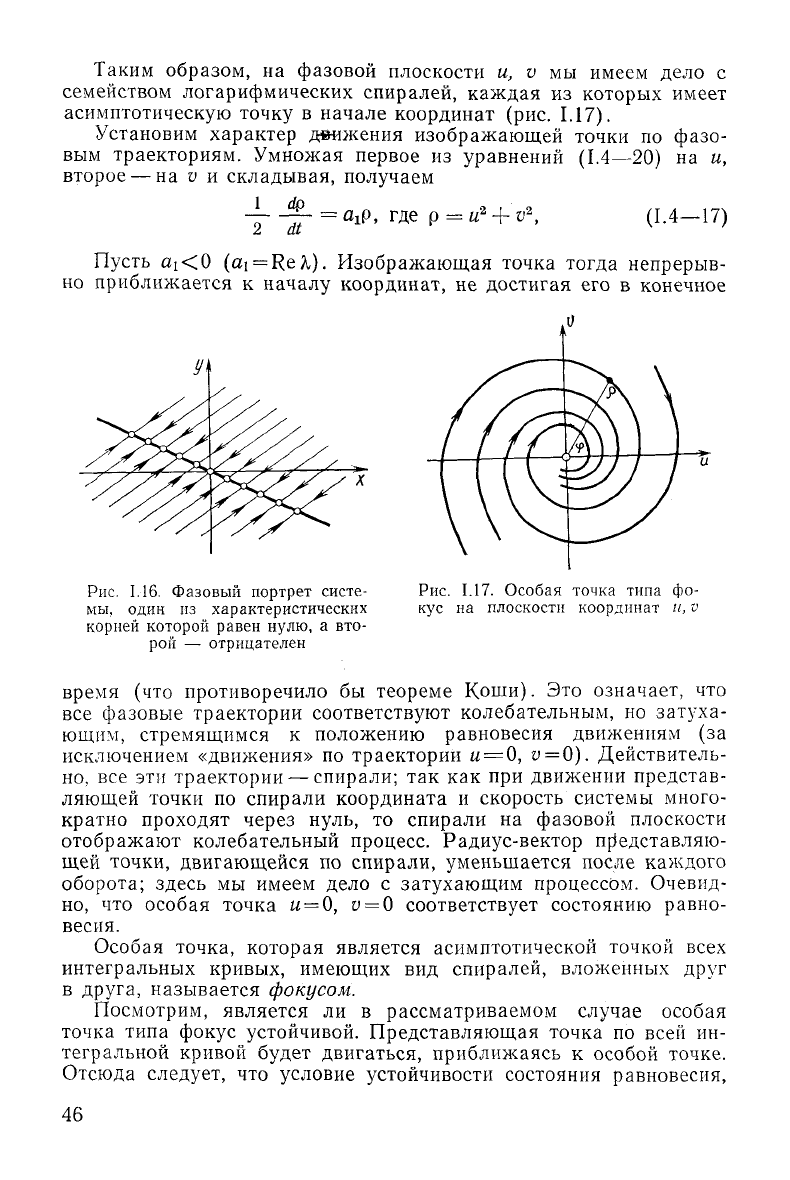
Таким

образом, на фазовой плоскости и, v мы имеем дело с

семейством логарифмических спиралей, каждая из которых имеет

асимптотическую точку в начале координат (рис.

1.17).

Установим характер движения изображающей точки по фазо-

вым траекториям. Умножая первое из уравнений

(1.4—20)

на и,

второе — на v и складывая, получаем

— -^г =

iP.

Де р = и

+ v

, (I.4—17)

Пусть ai<0 (ai = ReA). Изображающая точка

тогда

непрерыв-

но

приближается к началу координат, не достигая его в конечное

Рис.

1.16. Фазовый портрет систе-

мы,

один нз характеристических

корней

которой равен нулю, а вто-

рой

— отрицателен

Рис.

1.17. Особая точка типа фо-

кус на плоскости координат и, v

время (что противоречило бы теореме

Коши).

Это означает, что

все фазовые траектории соответствуют колебательным, но

затуха-

ющим,

стремящимся к положению равновесия движениям (за

исключением «движения» по траектории u = 0, v = 0). Действитель-

но,

все эти траектории — спирали; так как при движении представ-

ляющей точки по спирали координата и скорость системы много-

кратно

проходят через нуль, то спирали на фазовой плоскости

отображают колебательный процесс. Радиус-вектор представляю-

щей

точки, двигающейся по спирали, уменьшается после каждого

оборота; здесь мы имеем дело с затухающим процессом. Очевид-

но,

что особая точка а = 0, о = 0 соответствует состоянию равно-

весия.

Особая точка, которая является асимптотической точкой

всех

интегральных кривых, имеющих вид спиралей, вложенных

друг

друга,

называется

фокусом.

Посмотрим,

является ли в рассматриваемом

случае

особая

точка типа фокус устойчивой. Представляющая точка по всей ин-

тегральной кривой

будет

двигаться, приближаясь к особой точке.

Отсюда

следует,

что условие устойчивости состояния равновесия,

сформулированное нами в предыдущей главе, выполняется. Дей-

ствительно, мы всегда можем выбрать такую область б (двойная

штриховка), чтобы представляющая точка не вышла за пределы

области е (простая штриховка) (рис.

1.18).

случае

устойчивого фокуса, как и в

случае

устойчивого

узла,

выполнено

не только условие Ляпунова, но и более жесткое тре-

бование.

Именно,

при любых начальных отклонениях система по

прошествии достаточно длинного промежутка времени вернется

как

угодно близко к положению равновесия. Такую устойчивость,

при

которой начальные отклоне-

ния

не нарастают, а, наоборот, за-

тухают,

называют

абсолютной

ус-

тойчивостью.

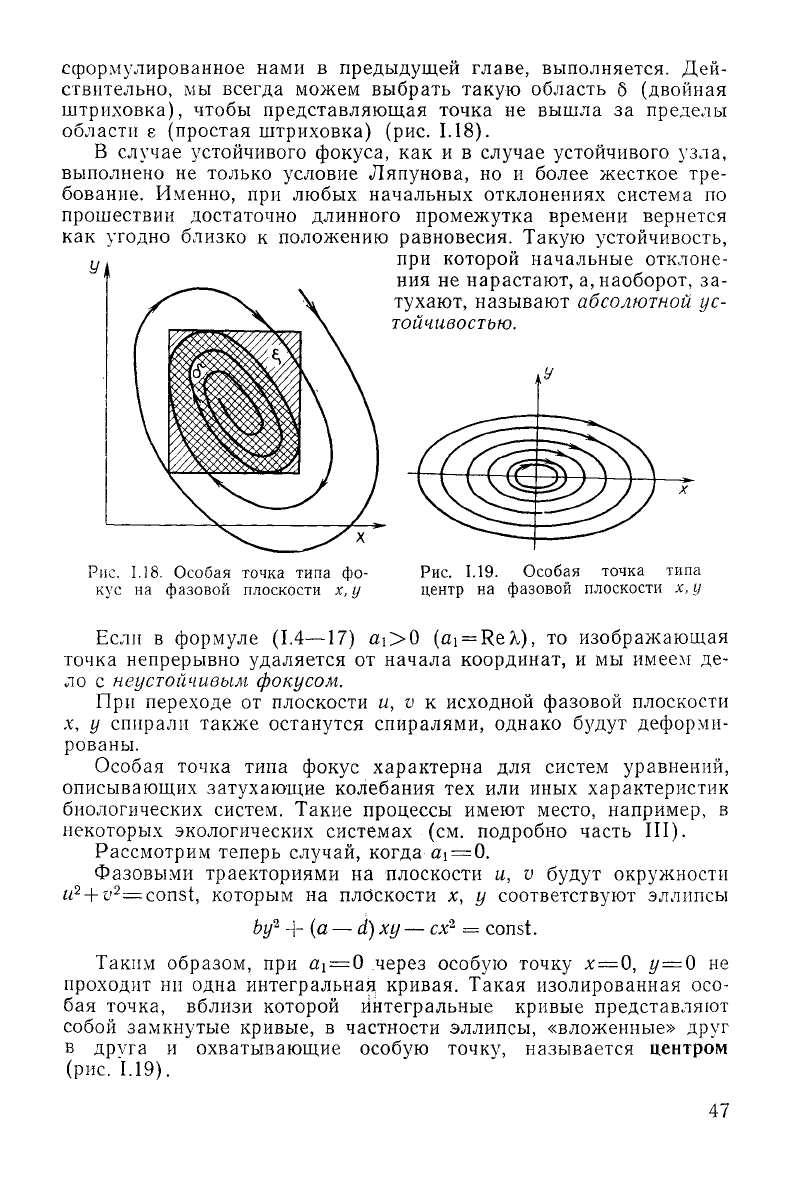
Рис.

1.18. Особая точка типа фо-

кус

на

фазовой

плоскости

х, у

Рис.

1.19. Особая точка типа

центр

на

фазовой

плоскости

х, у

Если

в формуле

(1.4—17)

а\>0 (ai = ReX), то изображающая

точка непрерывно удаляется от начала координат, и мы имеем де-

ло с

неустойчивым

фокусом.

При

переходе от плоскости и, v к исходной фазовой плоскости

х,

у спирали также останутся спиралями, однако

будут

деформи-

рованы.

Особая точка типа фокус характерна для систем уравнений,

описывающих затухающие колебания тех или иных характеристик

биологических систем. Такие процессы имеют место, например, в

некоторых экологических системах (см. подробно часть III).

Рассмотрим теперь случай, когда а\ = 0.

Фазовыми

траекториями на плоскости и, v

будут

окружности

+ i>

—const, которым на плоскости х, у соответствуют эллипсы

' + (a — d) xy — ex

= const.

Таким

образом, при «1 = 0 через особую точку х=0, г/=0 не

проходит ни одна интегральная кривая. Такая изолированная осо-

бая точка, вблизи которой интегральные кривые представляют

собой замкнутые кривые, в частности эллипсы, «вложенные»

друг

друга

и охватывающие особую точку, называется

центром

(рис.

"1.19).

Классическим

примером системы, имеющей своей особой точ-

кой

центр, является система Вольтерра, исследование которой мы

проведем подробно в следующей главе.

Сформулируем результаты нашего исследования. В рассмат-

риваемой линейной системе

=ах+Ьу,

-^- = cx + dy (I.4—1)

dt "' dt

случае

отсутствия вырождения (т. е. при

ad—ЬсфО)

возможно

шесть типов состояний равновесия в зависимости от характера

корней

характеристического уравнения

— Я (а + d) + (ad — be) = 0:

1) устойчивый

узел

(Я[ и Яг действительны и отрицательны);

2) неустойчивый

узел

(Ki и Яг действительны и положительны);

3) седло (Xi и Яг действительны и разных знаков);

4).

устойчивый фокус (Я] и Яг комплексны и ReX<0);

5) неустойчивый фокус (Х\ и Х

комплексны и ReX>0);

6) центр (Xi и Я

мнимые).

Первые пять типов состояния равновесия являются грубыми:

их характер не изменяется при достаточно малых изменениях пра-

вых частей уравнений

(1.4—1)

(малыми должны быть изменения

не

только правых частей, но и их производных первого порядка).

Связь

между

типами состояний равновесия и характером кор-

ней

характеристического уравнения может быть представлена на-

глядно следующим образом. Введем обозначения:

а = — (а + d); А =

Тогда характеристическое уравнение запишется в виде

-{- аХ + А = 0.

Для различных а и -А

будем

иметь различные корни Х\ и

Х%.

Рас-

смотрим плоскость с прямоугольными декартовыми координатами

сг и А и отметим на этой плоскости области, соответствующие тому

или

другому

характеру состояния равновесия.

Учтем

при этом,

что

— а ± Va

— 4 Д

42 = • -2

Условием устойчивости состояния равновесия является, как не-

трудно видеть, наличие отрицательной действительной части у Х\

Яг. Необходимым и достаточным условием для этого являются

неравенства а>0, Д>0. На диаграмме (рис. 1.20) этому условию

соответствуют точки, расположенные в первой четверти. Особая

точка

будет

типа фокус, если Xi и Яг комплексны. Этому условию

удовлетворяют те точки плоскости а, А, для которых а

—4Д<0,

т. е. точки, лежащие

между

ветвями параболы а

=4А. Точки полу-

оси

с=0, Д>0 соответствуют состояниям равновесия типа центр.

Аналогично Ki,

"k%

будут

действительны, но разных знаков, т. е. осо-

бая точка

будет

типа седла, если К\<0 и т. д. В итоге мы получим

диаграмму разбиения плоскости параметров о, А на области, соот-

ветствующие различным типам состояния равновесия.

Если

коэффициенты линейной системы

(1.4—1)

а, Ь, с, d зави-

сят от некоторого параметра, то при изменении этого параметра

будут

меняться соответственно а и А.

При

изменении соотношения

между

этими величинами проис-

ходит

изменение (деформация) фазового портрета. На плоскости

а, А поведение изучаемой системы

будет

характеризоваться некото-

рой

кривой, переходящей при би-

фуркационных значениях парамет-

ра из одной области в

другую

ска- _

чественным изменением фазового J

портрета. В процессе бифуркации

изменяется

тип особой точки. На ди-

аграмме видно, как

могут

происхо- у

дить такие изменения. Если исклю-

чить особые случаи (прохождение

через начало координат), то легко

видеть, что седло может перейти в

узел, устойчивый или неустойчи-

вый;

в свою очередь, устойчивый

Рис l2Q

Плоскость параметров

Устойчивый

узе/!

для системы уравнений

(1.4-1)

узел

может перейти либо в седло, д, а

либо в устойчивый фокус, и т. д.

Может также меняться характер

устойчивости особой точки: устойчивый фокус через центр может

переходить в неустойчивый фокус и обратно. Как при изменении

типа особой точки, так и при изменении характера ее устойчиво-

сти меняется топологическая

структура

фазовой плоскости в

окрестности особой точки. Заметим, что случай равных корней

(а

—4А=0) соответствует границе

между

узлами и фокусами.

Если

коэффициенты линейной системы зависят от

двух

парамет-

ров,

то обычно бывает целесообразно построить плоскость этих

параметров и на ней диаграмму, соответствующую только что

рассмотренной.

Для иллюстрации применения теории линейных дифференци-

альных уравнений рассмотрим простейшую систему химических

реакций

Вещество х притекает извне с постоянной скоростью, превращает-

ся

в соединение у и со скоростью, пропорциональной концентрации

последнего, выводится из сферы реакции. Все реакции имеют пер-

вый

порядок, за исключением процесса поступления х извне, про-

текающего с постоянной скоростью. Запишем соответствующую

систему уравнений:

— ь h •

(1.4—18)

y _ и ., и .,

Координаты

особой точки, т. е. стационарные концентрации ве-

ществ х и у, получим, приравняв нулю правые части уравнений

системы (1.4—18):

х=-^-,

У=—.

(1.4—19)

Рассмотрим фазовый портрет системы. Разделим второе урав-

нение

(1.4—18)

на первое, получим

dy __ k

x — k

y /j ^ go)

^o)

dx k-i — k

Уравнение

(1.4—20)

определяет поведение переменных на фа-

зовой плоскости. Нарисуем сначала главные изоклины на фазовой

плоскости.

Уравнение главной изоклины вертикальных касатель-

ных

dy ki

оо,

х= —

—\

а горизонтальных касательных

, y .

dx k

Отметим, что изоклина вертикальных касательных является в то

же время интегральной кривой.

Как

указывалось в предыдущей главе, особая точка лежит на

пересечении главных изоклин.

Определим теперь, под каким

углом

пересекаются координат-

ные

оси интегральными кривыми. Если х = 0, то

—У-

= — у.

dx k

Таким

образом, тангенс

угла

наклона касательной к интегральным

кривым

у = у(х), пересекающим ось ординат х = 0, отрицателен в

верхней полуплоскости (вспомним, что переменные х, у имеют зна-

чения

концентраций, и поэтому нас интересует лишь правый

верх-

ний

квадрант фазовой плоскости). При этом величина тангенса

угла

наклона касательной увеличивается с удалением от начала