Рубин А.Б., Пытьева Н.Ф., Ризниченко Г.Ю. Кинетика биологических процессов

Подождите немного. Документ загружается.

плоскость, разбитая

на

траектории,

дает

легко обозримый

портрет» системы:

она

позволяет сразу охватить

всю

совокупность

возможных движений (изменений переменных

х, у),

отвечающих

всевозможным начальным условиям. Часто фазовый портрет

си-

стемы можно построить,

не

решая уравнений

руководствуясь

только

их

видом. Этот путь позволяет сделать выводы

характе-

ре движений

без

знания аналитических решений исходной системы

уравнений

и,

следовательно, применим

в тех

случаях,

когда такие

аналитические решения

не

могут

быть найдены.

Итак,

перед нами встает задача построения фазового портрета

системы вида (1.3—1).

Для этого необходимо построить векторное поле направлений

траекторий системы

каждой точке плоскости

х, у.

Задавая

при-

ращение

А^>0, мы

получим

для х и у

соответственно приращения

Ах

и Ау,

которые найдем

из

общей системы

х,

у) At,

Q(x,y)At.

(1-3-2)

Очевидно,

что при Л/>0 в

зависимости

от

знаков

Р(х, у) и

Q{x,y)

приращения

Ах и Ау

могут

быть как положительными,

так и

отри-

цательными. Направление вектора

—— в

точке

(х, у)

зависит

от

знаков

функций

Р(х, у) и Q(x, у) в

этой

же

точке

может быть

задано такой таблицей:

(I)

Р(х,

у)>0, Q(x, г/)>0

P(x,y)<0,

Q(x,y)<0

(П)

(I)

(И)

Ау

Ах

P(x,y)>0, Q{x,y)<0

P(x,y)<0, Q(x,y)>0

(III)

(IV)

(III)

Ах

(IV)

Определив таким образом направления траекторий в каждой точ-

ке

фазовой плоскости, мы

будем

иметь полный фазовый портрет

системы. Нет нужды, однако, говорить, что построение такого век-

торного поля представляет собой слишком

трудоемкую

задачу.

Она

несколько упрощается, если получить выражение для фазо-

вых траекторий в аналитическом виде.

Вспомним,

что фазовая траектория имеет касательные, тангенс

угла

наклона которых в каждой точке М(х, у) равен значению

производной

в этой же точке —— (х, у). Следовательно, чтобы

ах

провести фазовую траекторию через точку фазовой плоскости

М\{х\,

г/]), достаточно знать направление касательной в этой точке

плоскости,

или значение производной

x=x

Для этого необходимо получить уравнение, содержащее перемен-

ные

х я у я не содержащее времени t в явном виде.

Чтобы из исходной системы уравнений

Р(х, У),

получить уравнение, связывающее непосредственно х и у, и, не

интегрируя уравнений, перейти к картине на фазовой плоскости,

разделим второе уравнение системы на первое. Получим диффе-

ренциальное уравнение

dy _ Q (х, у)

dx Р(х,

)

(1.3-3)

которое во многих случаях более простое, чем исходная система

второго порядка (1.3—1). Решение уравнения у=у(х, с), или в

неявной

форме F(x, y)=c, где с — постоянная интегрирования,

даст

нам семейство интегральных кривых — фазовых траекторий

системы

(1.3—3)

на плоскости х, у.

Однако часто построение полного фазового портрета системы,

е установление зависимости у=у(х, с), на всей плоскости х, у

представляет собой достаточно

трудную

задачу,

так как в общем

случае

уравнение

(1.3—3)

может и не иметь аналитического реше-

ния.

Тогда построение интегральных кривых производится каче-

ственно.

Для качественного построения фазового портрета системы

обычно пользуются методом изоклин. Метод заключается в том,

что на фазовой плоскости наносятся линии, которые пересекают

интегральные кривые только под одним определенным углом. Рас-

сматривая ряд изоклин, можно установить, каков

будет

ход самих

интегральных кривых.

Уравнение изоклин легко получить из уравнения (1.3—3). По-

ложим

где А — определенная постоянная величина. Значение А представ-

ляет собой тангенс

угла

наклона касательной к фазовой траекто-

рии

и, следовательно, может принимать значения от —оо до +оо.

Подставляя в

(1.3—3)

вместо —— величину Л, имеем уравне-

(XX

ние

изоклин

(

.з5)

Р(х,У)

Давая А определенные численные значения, получаем семейство

кривых. В любой точке каждой из этих кривых

угол

наклона каса-

тельной к фазовой траектории, проходящей через эту точку, равен

одной

и той же величине, а именно величине А, характеризующей

данную изоклину.

Отметим, что в

случае

линейных систем, т. е. систем типа

(1.3—1), правые части которых Р(х, у), Q(x, у) представляют

собой линейные относительно х, у формы, изоклины представляют

собой пучок прямых, проходящих через начало координат. Так,

если изучаемая нами система описывается линейными уравнения-

ми

вида

=ax+by,

(I.3—6)

cx -j- dy,

уравнение изоклин можно записать в следующем виде:

схЛ-dy

. (Аа — с)х /

7Ч

—

•• = А, или у = — —.

(1.3—7)

ах+Ьу d — Ab

Уравнение

(1.3—3)

непосредственно определяет в каждой точ-

ке

плоскости единственную касательную к соответствующей инте-

гральной кривой. Исключение составляет точка пересечения

всех

изоклин,

в которой направление касательной становится неопре-

деленным, так как при этом становится неопределенным значение

производной

Q(x, у) °

P(x, y)' °

(1.3-8)

Точки,

в которых одновременно обращаются в нуль производные

по

времени переменных х и у

. = P (x, У) - 0,

x, у

в которых направление касательных к интегральным кривым

неопределенно,

носят название особых точек. Особая точка урав-

нения

фазовых траекторий

(1.3—3)

соответствует стационарному

состоянию системы (1.3—1), так как скорости изменения перемен-

ных в этой точке равны нулю, а ее координаты

суть

стационарные

значения

переменных х, у.

Для качественного изучения часто можно ограничиться построе-

нием

не

всех,

а лишь некоторых изоклин на фазовой плоскости.

Особый интерес представляют так называемые

главные

изоклины:

—— = 0 — изоклина горизонтальных касательных к фазовым тра-

екториям,

уравнение которой

Q (х, у) = 0,

изоклина вертикальных касательных—

- =оо, которой соответ-

ах

ствует

уравнение Р(х, у) =0.

Построив

главные изоклины и найдя точку их пересечения

(х,

у), координаты которой удовлетворяют условиям

мы определим тем самым точку пересечения

всех

изоклин фазовой

плоскости,

в которой направление касательных к интегральным

кривым

неопределенно:

Р(х, у)

у)

Она

является, как уже говорилось, особой точкой и соответствует

стационарному состоянию системы.

Система уравнений

(1.3—1)

обладает

столькими стационарны-

состояниями,

сколько точек пересечения главных изоклин

имеется

на

фазовой плоскости.

Вопросам исследования свойств стационарных состояний

си-

стем, описываемых системами дифференциальных уравнений

вто-

рого' порядка,

будут

посвящены

две

следующие

главы,

сейчас

мы остановимся

на их

общих свойствах.

Итак,

мы

рассматриваем систему

двух

автономных дифферен-

циальных уравнений первого порядка

JjL-=P(x,y),

-jt-^Q(x,y),

(I.3-1)

описывающих некоторую динамическую систему второго порядка,

предполагая,

что

состояния этой системы взаимно однозначно

непрерывно

соответствуют

точкам фазовой плоскости

х, у.

Функ-

ции

Р(х, у), Q(x, у) мы

полагаем непрерывными

имеющими

непрерывные частные производные

не

ниже первого порядка:

dP dQ dQ

dy dx dy

Пусть условия теоремы Коши

существовании

единственности

решения

системы дифференциальных уравнений

для

(1.3—1)

вы-

полнены,

поэтому

существует

единственная система функций

x(t),

y = y(t),

удовлетворяющая уравнениям

(1.3—1)

начальным условиям

у = у

при

=---1

Так

как

решение зависит

от

начальных условий,

то

иногда,

чтобы подчеркнуть

это

обстоятельство, решение записывается

следующем

виде:

<p(t

—1

Л'

, г/

);

y = y(t — t

, х

(1.3—9)

Отметим,

что ср и

-ф

являются аналитическими функциями

не

толь-

ко

времени

t, но и

координат начального состояния системы

, г/о-

Как

показано выше, всякое решение системы уравнений

(1.3—1)

с заданными

, у

, t

можно рассматривать

как

параметрическое

уравнение (параметром здесь является время

некоторой кривой

на

фазовой плоскости

х, у,

которая пробегается изображающей

точкой

при

заданном движении системы. Такие траектории носят

название

фазовых траекторий.

другой

стороны, решение

(1.3—9)

мы

может рассматривать

как

уравнение кривых

пространстве

х, у, t, т. е.

интегральных

кривых системы уравнений (1.3—1). Ясно,

что

каждая фазовая

траектория,

т. е.

кривая

у = у(х),

является проекцией

на

фазовую

плоскость

х, у

некоторой интегральной кривой

пространстве

У>

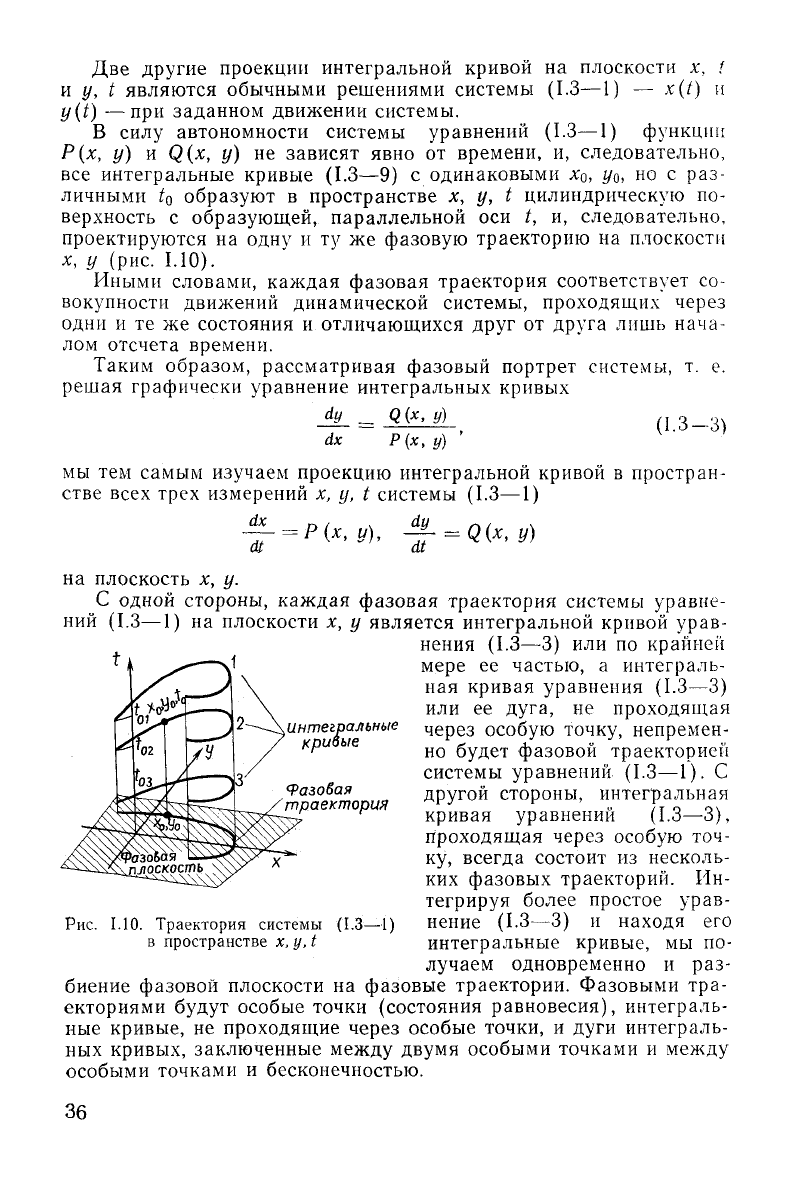
Две

другие

проекции интегральной кривой на плоскости х, t

у, t являются обычными решениями системы

(1.3—1)

— x(t) и

y(t)

—при заданном движении системы.

В силу автономности системы уравнений

(1.3—1)

функции

Р(х, у) и Q{x, у) не зависят явно от времени, и, следовательно,

все интегральные кривые

(1.3—9)

с одинаковыми х

, г/о. но с раз-

личными

образуют в пространстве х, у, t цилиндрическую по-

верхность с образующей, параллельной оси t, и, следовательно,

проектируются на одну и ту же фазовую траекторию на плоскости

х,

у (рис.

1.10).

Иными

словами, каждая фазовая траектория соответствует со-

вокупности движений динамической системы, проходящих через

одни

и те же состояния и отличающихся

друг

от

друга

лишь нача-

лом отсчета времени.

Таким

образом, рассматривая фазовый портрет системы, т. е.

решая графически уравнение интегральных кривых

Q(x, у) ,j

dx P(x, у) '

мы тем самым изучаем проекцию интегральной кривой в простран-

стве

всех

трех

измерений х, у, t системы

(1.3—1)

на

плоскость х, у.

одной стороны, каждая фазовая траектория системы уравне-

ний

(1.3—1)

на плоскости х, у является интегральной кривой урав-

нения

(1.3—3)

или по крайней

мере ее частью, а интеграль-

ная

кривая уравнения

(1.3—3)

или

ее

дуга,

не проходящая

через особую точку, непремен-

но

будет

фазовой траекторией

системы уравнений (1.3—1). С

другой

стороны, интегральная

кривая

уравнений (1.3—3),

проходящая через особую точ-

ку, всегда состоит из несколь-

ких фазовых траекторий. Ин-

тегрируя более простое урав-

нение

(1.3—3)

и находя его

интегральные кривые, мы по-

интегральные

кривые

Фазовая

траектория

Рис.

1.10.

Траектория

системы (1.3—1)

пространстве х, у, t

лучаем одновременно и раз-

биение

фазовой плоскости на фазовые траектории. Фазовыми тра-

екториями

будут

особые точки (состояния равновесия), интеграль-

ные

кривые, не проходящие через особые точки, и

дуги

интеграль-

ных кривых, заключенные

между

двумя особыми точками и

между

особыми точками и бесконечностью.

Уравнение интегральных кривых

(1.3—3)

не

дает

нам никаких

указаний о направлении движения изображающей точки по най-

денным фазовым траекториям, так как время из него исключено.

Направление

движения изображающей точки определяется изурав-

" /ТО 1 \

нении

(1.0—

I).

Так

как условия теоремы Коши для системы уравнении

(1.3—1)

выполнены,

то через каждую точку пространства х, у, t проходит

единственная интегральная кривая этой системы уравнений, т. е.

интегральные кривые в пространстве х, у, t пересекаться не

могут.

То же самое, благодаря автономности уравнений (1.3—1), можно

сказать и о фазовых траекториях: они также не

могут

пересекать-

ся,

ибо через каждую точку фазовой плоскости проходит един-

ственная

фазовая траектория. В силу только что указанного свой-

ства фазовых траекторий изображающая точка, двигаясь по дру-

гим фазовым траекториям, не может прийти в состояние равно-

весия

ни при каком конечном t. Установление состояний равно-

весия

в динамических системах, описываемых уравнениями

(1.3—1)

с правыми частями, удовлетворяющими условиям теоремы

Коши,

происходит только асимптотически (только при t—>oo).

случае

произвольного вида функций Р(х, у) и Q(x, у) в пра-

вых частях уравнений системы

(1.3—1)

исследование фазовых тра-

екторий

представляет значительные трудности. Однако, как и в

случае

одного уравнения (см. гл. 2), характер поведения системы

основном определяется количеством, местом расположения на

фазовой

плоскости и типом устойчивости стационарных состояний

системы. - . ...:

В предыдущей главе мы дали определение устойчивости ста-

ционарного

решения одного уравнения. В рассматриваемом нами

здесь

случае

системы

двух

уравнений удобно дать определение

устойчивости стационарного состояния, используя для этой цели

уже введенное нами представление о фазовой плоскости.

Пусть рассматриваемая система находится в состоянии равно-

весия.

Тогда изображающая точка на фазовой плоскости находит-

ся

в неподвижности в одной из особых точек уравнения интеграль-

ных кривых (1.3—3), так как в этих точках, по определению,

dt dt

Если

теперь мы выведем нашу систему из состояния равновесия,

то изображающая точка сместится из особой точки и начнет дви-

гаться по фазовой плоскости в соответствии с уравнениями ее дви-

жения

£-*>(«.

Й.

-*•-«<*. Й.

Устойчива или нет рассматриваемая нами особая точка систе-

мы определится тем,

уйдет

или нет изображающая точка из не-

которой данной области, окружающей особую точку, причем эта

область может быть большей или меньшей в зависимости от усло-

вий

задачи. Применительно к системе

двух

уравнений определе-

ние

устойчивости на языке г, б выглядит следующим образом:

Состояние

равновесия является устойчивым, если для любой

заданной

области допустимых отклонений от состояния равновесия

(область е) мы можем указать об-

ласть б(е), окружающую состояние

равновесия и обладающую тем

свойством, что ни одно движение

изображающей точки, начинающее-

ся

внутри б, никогда не достигнет

границы

области е. Наоборот, со-

стояние

равновесия неустойчиво, ес-

ли

может быть указана такая об-

ласть отклонений от состояния рав-

новесия

е, для которой не сущест-

вует

области б(е), окружающей со-

Л стояние равновесия и обладающей

тем свойством, что ни одно движе-

ние,

начинающееся внутри б, ни-

когда не достигнет границы г

(рис.

I.ll.a).

Можно

записать это определе-

ние

устойчивости на языке математических неравенств, предполо-

жив для простоты, что область допустимых отклонений е представ-

ляет собой квадрат (рис. I. 11,6).

Мы

получим такую формулировку нашего определения:

Состояние

равновесия х = х, у=у устойчиво, если для любого

заданного наперед сколь угодно малого е (е>0) можно при / = 0

найти

такое б>0, что если при

= 0 начальное отклонение пере-

менных от равновесных значений мало и выполняются неравен-

ства

|х(0) — х|<6 И \у(0) — у\<6,

(1.3—10)

то для любого последующего момента времени

0<£<

+ оо

будут

справедливы неравенства

\x(t)—x\<s

и \y{t) —

y\<e.

Рис.

1.11. Иллюстрация к опреде-

лению устойчивости.

Области

е и

б на плоскости х, у

(1.3-11)

Иными

словами, все последующие отклонения значений перемен-

ных от равновесных также

будут

малыми.

Вспомним,

что в автономных системах первого порядка изме-

нение

переменной может носить лишь монотонный характер — она

с течением времени либо приближается к своему стационарному

состоянию (состояние равновесия устойчиво), либо удаляется от

него (состояние равновесия неустойчиво). В отличие от систем

первого порядка характер поведения переменных в системах вто-

пого порядка может быть более разнообразным: иметь как моно-

тшный так и немонотонный (например колебательный) харак-

тер Однако и для системы

двух

уравнений, как

будет

показано

в дальнейшем, существенную информацию о поведении системы

в целом и, в частности, о характере состояний равновесия в боль-

шом числе случаев можно получить, исследуя не исходную систему

/j 3 1), а упрощенную, линеаризованную систему уравнений типа

(L3-6)!

Для некоторого класса систем, а именно

грубых

систем,

харак-

тео поведения которых не меняется при малом изменении вида

уравнений (1.3—1), дело сводится к исследованию состояний рав-

новесия такого рода линеаризованной системы. Процесс линеари-

зации

системы

двух

уравнений общего вида

будет

изложен подроб-

но

в гл. 5.

Следующая глава посвящена рассмотрению возможных типов

состояний равновесия в линейных системах и классификации осо-

бых точек.

Глава

ЛИНЕЙНЫЕ

СИСТЕМЫ.

ТИПЫ

ОСОБЫХ ТОЧЕК:

УЗЕЛ,

СЕДЛО,

ФОКУС,

ЦЕНТР.

ПРИМЕР:

ХИМИЧЕСКИЕ

РЕАКЦИИ

ПЕРВОГО

ПОРЯДКА

Рассмотрим простейшие динамические системы вида (1.3—1),

которые отображаются двумя линейными дифференциальными

уравнениями первого порядка (см.

1.3—6):

где а, Ъ, с, d — константы, ахи у— декартовы координаты на фа-

зовой плоскости.

Общее решение системы

будем

искать в виде

= Ае

, у = Ве

(1.4—2)

Подставим эти выражения в

(1.4—1)

и сократим полученные вы-

ражения на е

ХА = аА + ЬВ,

(1.4-3)

KB = cA + dB.

Алгебраическая система уравнений

(1.4—3)

с неизвестными А, В

имеет, как известно, ненулевое решение лишь в том случае, если

ее определитель, составленный из коэффициентов при неизвестных,

равен нулю:

а — X b

/тло\

0. (1.4—За)

d —

Раскрывая

этот определитель, получим так называемое характе-

ристическое уравнение системы (1.4—1):

— (а ~\- d) X -\- (ad — be) = 0.

(1.4—4)

Решение

этого уравнения

дает

значения показателя Х\$, при кото-

рых возможны ненулевые для А и В решения уравнения (1.4—3):

Отметим, что если подкоренное выражение отрицательно, "м,2—

комплексно-сопряженные

числа. Предположим, что оба корня урав-

нения

(1.4—4)

имеют отличные от нуля действительные части и

что нет кратных корней. Тогда общее решение системы (1.4—1),

записанное

в виде (1.4—2), можно представить линейной комби-

нацией

экспонент с показателями %i и 1

(1.4-6)

—

"Л

е>

* +

е>

'•

Для анализа характера возможных траекторий системы

(1.4—1)

на

фазовой плоскости используем линейное однородное преобразо-

вание координат. Такое преобразование позволит привести систе-

му

(1.4—1)

к так называемому каноническому виду

допускающему более удобное представление на фазовой плоско-

сти по сравнению с исходной системой (1.4—1). Введем новые ко-

ординаты |, Ti по формулам

g = co:+P«/,

У]

= ух+8у.

(1-4-8)

Из

курса линейной алгебры известно, что в

случае

неравенства

нулю действительных частей Ль А.2 (ReAi,2=7^=0) исходную систему

(1.4—1)

при помощи преобразований

(1.4—8)

всегда можно при-

вести к каноническому виду

(1.4—7)

и изучать ее поведение на фа-

зовой плоскости |, ц.

Рассмотрим различные случаи, которые

могут

здесь предста-

виться.