Рубин А.Б., Пытьева Н.Ф., Ризниченко Г.Ю. Кинетика биологических процессов

Подождите немного. Документ загружается.

где

/'(*). «2 = — /"(*) и т. д.

Отбросим в уравнении

(1.2—4)

нелинейные члены как величи-

ны

более высокого порядка малости. Мы получим

тогда

линейное

уравнение

(5)

dt '

которое носит название линеаризованного уравнения, или уравне-

ния

первого приближения. Интеграл этого уравнения для £(/)

находится сразу:

КО

= Се", где X = а

= /' (х), С = const.

Если

к<0, то при

t-*-oo

£->-0,

а следовательно, первоначальное

отклонение

| от равновесия со временем самопроизвольно

затухает

силу характера поведения нашей системы. Таким образом, ста-

ционарное

решение х=х уравнения

(1.2—1)

устойчиво по Ляпу-

нову. Наоборот, если Х>0, то при

£->~оо

g->oo и исходное состоя-

ние

равновесия неустойчиво. Если Х=0, то уравнение первого при-

ближения,

вообще говоря, не может дать ответа на вопрос об

устойчивости исходной системы.

Метод Ляпунова позволяет по знаку производной f(x) правой

части исходного уравнения получить правильный ответ на вопрос

об устойчивости его точек равновесия. В рассматриваемом простом

случае

нетрудно строго доказать справедливость этого метода ис-

следования устойчивости. Умножая обе части уравнения

(1.2—4)

на

будем

иметь

или

т ~iF~

=ai

+а

• •

•

= F {l)

(L2

Представим .F(£) при помощи теоремы Тейлора:

||),

где 0<6< 1.

Здесь '—'— g

— остаточный член в формуле Тейлора. Заме-

тим,

что F(0) =0, F'{0) =0; F"(0)

=2а

Положим р = — I

тогда

Уравнение

(1.2—6)

примет вид

dt 2

Если

F"(0)<0 (или, что то же самое, ai<0), то в силу непре-

рывности функций

F"(%)<0

f"(0£)<O

для достаточно малых

|||. Отсюда

следует

из (1.2—7), что и—^-<0 для тех же |||. Если

— —£

уменьшается, то уменьшается и ||| и никогда не может

начать увеличиваться. Отсюда

следует,

что условие

% = /' (х) < 0

(1.2-8)

достаточно для устойчивости по Ляпунову рассматриваемого со-

стояния

равновесия х=х, так как в этом

случае

всегда

существует

такая

область начальных значений, из которой наша система бу-

дет асимптотически приближаться к состоянию равновесия.

Аналогичным путем можно показать, что при ai =

f'(x)>0

со-

стояние

равновесия х = х неустойчиво по Ляпунову.

Таким

образом, метод Ляпунова оправдывается, и

результат

исследования устойчивости состояния равновесия при помощи пол-

ного нелинейного дифференциального уравнения для %(t)

совпадает с результатом исследования устойчивости при помощи

линейного

уравнения

—^- =

flig,

если a^^O.

Аналогичные рассуждения

будут

полезны при рассмотрении

более сложных динамических систем. Вместе с тем в

случае

одно-

го уравнения нетрудно, исследуя непосредственно характер функ-

ции

f(x) вблизи состояния равновесия х

—

х, однозначным образом

решить вопрос об устойчивости состояния равновесия.

По

определению, в особой точке функция f(x)

-, -. dx

(

) =

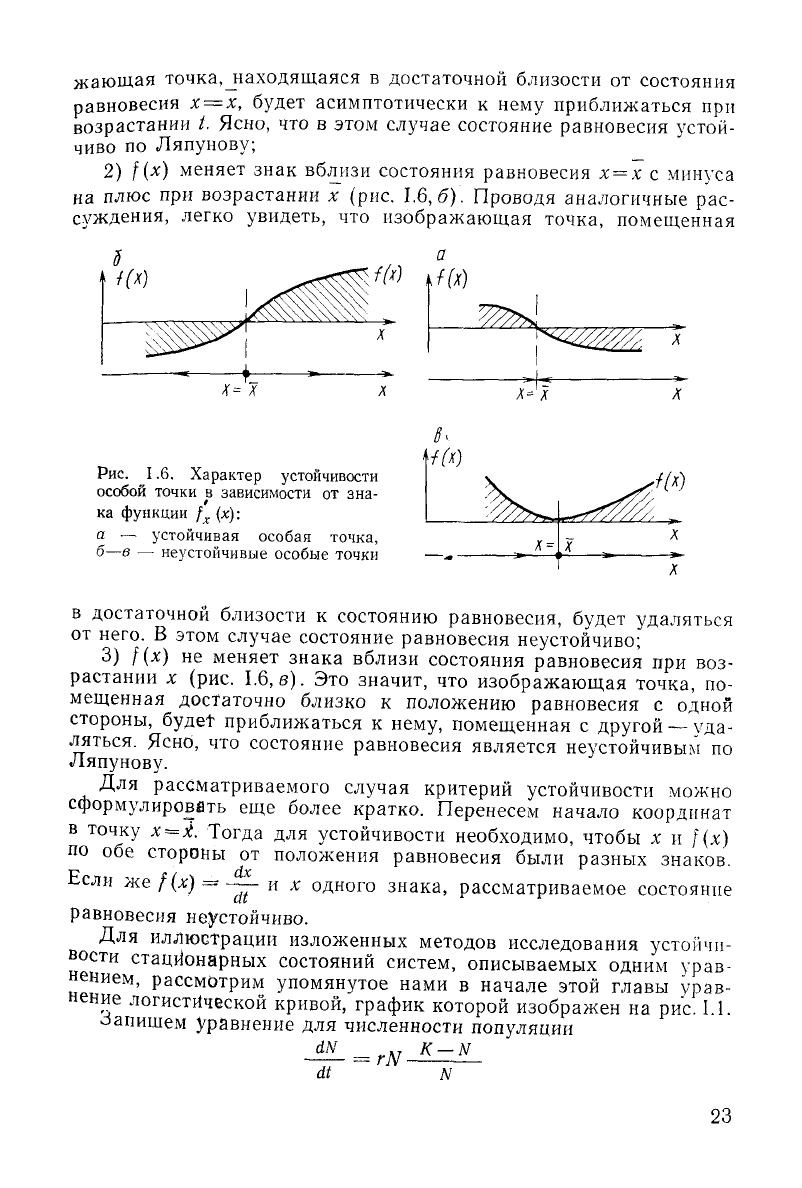
обращается в нуль. Здесь возможны три различных случая (рис.

1.6):

1) вблизи состояния равновесия x=xf(x) меняет знак с плю-

са на минус при возрастании х (см. рис. 1.6, а).

Такое изменение знака f(x) в точке х = х означает, что при

х<х скорость изменения =f(x) положительна. При этом х

увеличивается, т. е. стремится к х. Прих>х

> Т

е х

уменьшается и опять стремится к х. Отсюда

следует,

что изобра-

жающая точка,находящаяся в достаточной близости от состояния

равновесия х = х,

будет

асимптотически к нему приближаться при

возрастании t. Ясно, что в этом

случае

состояние равновесия устой-

чиво по Ляпунову;

2) f(x) меняет знак вблизи состояния равновесия х = х с минуса

на

плюс при возрастании х (рис.

1.6,6).

Проводя аналогичные рас-

суждения, легко

увидеть,

что изображающая точка, помещенная

i(X)

Рис.

1.6. Характер устойчивости

особой

точки в зависимости от зна-

ка

функции f

(x):

а — устойчивая особая точка,

б—в — неустойчивые особые точки

достаточной близости к состоянию равновесия,

будет

удаляться

от него. В этом

случае

состояние равновесия неустойчиво;

3) f(x) не меняет знака вблизи состояния равновесия при воз-

растании х (рис. 1.6, в). Это значит, что изображающая точка, по-

мещенная

достаточно близко к положению равновесия с одной

стороны,

будет

приближаться к нему, помещенная с

другой

— уда-

ляться.

Ясно, что состояние равновесия является неустойчивым по

Ляпунову.

Для рассматриваемого случая критерий устойчивости можно

сформулировать еще более кратко. Перенесем начало координат

точку х = х.

Тогда

для устойчивости необходимо, чтобы х и f (х)

по

обе стороны от положения равновесия были разных знаков.

Если

же/(*) = -—и х одного знака, рассматриваемое состояние

равновесия неустойчиво.

Для иллюстрации изложенных методов исследования устойчи-

вости стационарных состояний систем, описываемых одним урав-

нением,

рассмотрим упомянутое нами в начале этой главы урав-

нение

логистической кривой, график которой изображен на рис. 1.1.

•запишем

уравнение для численности популяции

., к — N

стандартном виде, переобозначив тождественно N==x. Тогда в

соответствии с уравнением

(1.2—1)

мы

будем

иметь

(1-2—9)

f()

dt ' К

Легко видеть, что уравнение стационарных состояний

f(x)=O

данном

случае

имеет два

корня:

= К.

Посмотрим,

являются ли эти корни устойчивыми. Для этого вна-

чале воспользуемся аналитическим методом Ляпунова. Введем

новую переменную |, описывающую отклонение переменной от ее

стационарного значения:

| = X — X.

Запишем

линеаризованное уравнение вида

(1.2—5)

для уравнения

(1.2-9):

f- =а%, где а = /'

Напомним,

что знак величины а(х

{

) определяет устойчивость со-

ответствующей особой точки Xf.

г-^-.

(1.2-10)

Подставив в выражение

(1.2—10)

значение первого корня Xi = 0,

мы получим

a(xi)=r.

Эта величина всегда положительна, так как,

по

определению, коэффициент естественной скорости роста популя-

ции

г>0. Следовательно, Xj =

— неустойчивая особая точка. Если

же мы подставим в выражение

(1.2—10)

Х2

= К, то получим а(х

) =

—г — отрицательную величину. Это

дает

нам право

утверждать,

что решение уравнения

(1.2—9)

— К является устойчивым, т. е.

соответствует устойчивому стационарному режиму — режиму суще-

ствования популяции в ограниченной среде.

Проведем теперь исследование устойчивости стационарных ре-

шений

этого уравнения исходя из графика функции f{x).

Из

рис. 1.7 видно, что в точке

JCI

(при переходе от отрица-

тельных к положительным значениям х) функция f(x) меняет знак

с минуса на плюс, т. е. особая точка является неустойчивой. В точ-

ке

Х2~К имеет место обратное изменение знака f(x) с ростом х —

с плюса на минус, следовательно, эта особая точка устойчивая.

Рассмотрим еще один пример — упрощенную модель проточно-

го культиватора, в котором происходит размножение бактериаль-

ных клеток,

их

гибель и, кроме того, имеет место приток клеток

извне

постоянной скоростью. Пусть скорость гибели клеток про-

порциональна

их

концентрации,

скорость размножения — квад-

рату

концентрации клеток (в двуполой

культуре

скорость размно-

жения

пропорциональна вероятности

встречи

двух

клеток разного пола).

f<x)

rx-

Тогда

дифференциальное уравнение,

описывающее изменение концентрации

живых клеток

такой системе,

будет

иметь вид

к-х

(1.2

Рнс.

1.7.

График функции

{(х)

для уравнения

(1.2—7)

Здесь а—скорость притока,

у,

Ь—ко-

эффициенты

размножения

гибели

клеток

соответственно. Для простоты

положим

у=\.

Рассмотрим характеристики стационарных состояний такой си-

стемы

зависимости от величины скорости притока

а.

Стационар-

ные

значения клеточных концентраций найдем

из

уравнения

f(c, a) =0. Их два:

^=4-+l/-f~-«.

H.2-12)

По

смыслу стационарные концентрации С\,

должны быть

действительными числами,

отсюда

видно, что при <х> сташю-

нарное

состояние не может быть

достигнуто

системе. При

а=—

имеется лишь одно стационарное состояние

i -"= с*.

-••

—,

а при

а<

системе возможны два стационарных режима

Это

соответствует

двум

ветвям стационарных состояний на графи-

ке,

по оси абсцисс которого отложены значения скорости притока

(рис.

1.8).

Ветви

стационарных состояний

С\

(а)

(а) отлича-

ются

друг

от

друга

по

характеру

устойчивости. Производная пра-

вой

части (1.2—Ц) для ветви F

{

(a) равна

a) =

а для ветви с

(a) равна

a) =-2 |/ — a

Согласно условию

(1.2—8)

отсюда

следует,

что все значения

С!

(а) являются неустойчивыми, а с

(а) —устойчивыми стационар-

ными

концентрациями.

Итак,

при а>—— стационарных решении в положительном

квадранте нет, при а= в этой области имеется одно стацио-

нарное

состояние с= —на границе устойчивости, наконец, при

a <—в системе имеются два стационарных состояния, причем

одно из них устойчивое,

другое

неустойчивое.

Вообще говоря, в любой системе вида

-j~ =

f(x,a),

(I.2-14)

где а — параметр, при изменении значения а интегральные кри-

вые

будут

так или иначе меняться. Однако при непрерывном изме-

нении

а общий вид кривых

будет

претерпевать лишь количествен-

ные

изменения. Только при некоторых особых, бифуркационных

значениях

параметра а мы

будем

иметь качественные изменения

характера интегральных кривых, т. е. изменение числа особых

точек и характера их устойчивости. Именно таким бифуркацион-

ным

значением параметра и является а= .Прочие значения a

называются обыкновенными. Понятия бифуркационных и обыкно-

венных значений параметра можно сформулировать более строго.

Значение

параметра a = ao является обыкновенным, если сущест-

вует

такое положительное е>0, что для всех а таких, что

|а—ао|<е,

имеет место одна и та же топологическая структура

фазовой

плоскости.

Другие

значения, для которых это условие

не

соблюдается, называют бифуркационными (Андронов, Витт,

Хайкин,

1959).

График,

построенный в координатах (а, х) для уравнения

—

=/(*, ос),

называется бифуркационной диаграммой (см. рис. 1.8). Такая диа-

грамма наглядно иллюстрирует зависимость положений равновесия

системы от параметра а.

Как

было показано выше, характер устойчивости стационарной

точки ~х уравнения

(1.2—14)

можно выяснить, определив в этой

точке знак производной f

(х, а).

Стационарные значения х=х находятся из уравнения f(x, a) =

0. В зависимости от вида функции f(x, а) это уравнение может

иметь один или несколько корней при одном и том же значении

параметра а. Так^если f(x, а)—полином х степени больше еди-

ницы,

кривая х = х(а)

будет

иметь такой вид, что некоторым зна-

Рис.

1.8. Зависимость ста-

ционарной

концентрации

клеток

С от параметра а

для уравнения

(1.2—11)

Рис.

1.9. Зависимость правой

части уравнения

(1.2—14)

от

параметра а

чениям а

будет

соответствовать несколько стационарных состоя-

ний

х. На рис. 1.9 изображена кривая стационарных состояний

х{а), согласно которой при а = ао

существуют

три различных ста-

ционарных режима (а, Ь, с). Найдя знак производной

(x,a)

Для каждой из точек (а, Ь, с), можно определить, какие из них

соответствуют

устойчивым стационарным состояниям. На рис. 1.9

приведен случай, когда

/* (х

, а) < 0, /.; {х

, а) > 0, f'

(х~

а) < 0.

Это означает, что а, с — устойчивые, а Ь — неустойчивое состоя-

ние.

Дуги

кривой АВ и DC представляют собой ветви устойчивых,

ВС — ветвь неустойчивых стационарных состояний. Бифуркаци-

онные значения параметра а, при которых изменяется число ста-

ционарных состояний с одновременным изменением типа устойчи-

вости, на рисунке обозначены а' и а".

Наличие

нескольких возможных стационарных состояний в си-

стеме при одних и тех же значениях параметров, так называемая

множественность стационарных состояний, представляет собой

одно из наиболее важных свойств биологических систем. Сущест-

вование в системе

двух

или нескольких устойчивых стационарных

состояний

обусловливает способность системы к переключениям и

проявлению триггерных свойств, на чем мы остановимся в даль-

нейшем.

Пока ограничимся тем, что поясним с помощью рис. 1.9,

как

наличие нескольких возможных стационарных состояний ска-

зывается на поведении системы.

Допустим, что при значении параметра а = ао система находит-

ся

в особой точке верхней устойчивой ветви АВ. Пусть каким-то

образом, независимо от процессов, описываемых дифференциаль-

ным

уравнением (1.2—14), происходит уменьшение величины ее.

При

этом система

будет

последовательно проходить через ряд

стационарных состояний, двигаясь вдоль ветви АВ. В точке В, со-

ответствующей

«стыку»

устойчивой (АВ) и неустойчивой (ВС)

ветвей, произойдет скачкообразный переход на нижнюю устойчи-

вую ветвь DC.

Увеличивая значение параметра а, можно перевести систему

вдоль устойчивой ветви DC до бифуркационной точки с, после

чего скачкообразно вернуть ее на исходную ветвь СВ. Таким обра-

зом осуществляется замкнутый гистерезисный цикл

(ABDCA),

котором в процессе изменения параметра система проходит ряд

стационарных состояний, отличающихся

друг

от

друга

при одних

тех же значениях а в зависимости от направления движения.

Направление

скачкообразных переходов зависит от того, происхо-

дит уменьшение или увеличение параметра а при приближении

бифуркационной точке.

Глава

СИСТЕМЫ

ДВУХ

ДИФФЕРЕНЦИАЛЬНЫХ

УРАВНЕНИЙ

ПЕРВОГО

ПОРЯДКА.

ФАЗОВЫЙ

ПОРТРЕТ

СИСТЕМЫ.

ОПРЕДЕЛЕНИЕ

УСТОЙЧИВОСТИ

В предыдущей главе мы познакомились с методами исследова-

ния

математических моделей, представляемых одним дифферен-

циальным

уравнением первого порядка. Теперь мы рассмотрим

основы

теории систем, описываемых двумя уравнениями первого

порядка.

Такие

системы уравнений

могут

описывать гораздо более широ-

кий

класс биологических явлений, чем уравнения первого порядка.

В частности, в таких системах возможны автоколебания, т. е. пе-

одические изменения переменных

постоянной амплитудой.

Напомним,

что решения одного уравнения вида

f(x)

(I.2-1)

всегда являются монотонными, следовательно, не

могут

описывать

какой

бы

то

ни было реальный периодический процесс. Обладая

достаточно общими свойствами, системы

двух

уравнений первого

порядка

то же время допускают наглядное представление пове-

дения

переменных

на

фазовой плоскости. Исследование систем

более высокого порядка, как правило, сложнее,

решать

их

при-

ходится численно при помощи ЭВМ; общность

наглядность при

этом,

естественно, теряются.

Именно

поэтому исследователи стараются, когда это возмож-

но,

сводить

исследуемую

систему более высокого порядка

двум

уравнениям (Романовский, Степанова, Чернавский, 1975).

Как

мы

увидим

дальнейшем, системами второго порядка

описываются модели темновых процессов фотосинтеза, процессы

конкуренции,

хищничества

другие

экологические модели. При

исследовании свойств этих моделей используются методы каче-

ственной

теории дифференциальных уравнений, существенно бази-

рующиеся на представлении

фазовом портрете системы. Поэтому

этой

следующих

главах

мы остановимся на некоторых общих

свойствах систем второго порядка, описываемых

общем виде

уравнениями

£ =

<*•*>•

(1.3-1)

Здесь Р(х,

у),

Q(x, у)—непрерывные функции, определенные

некоторой

области

евклидовой плоскости (х,

— декартовы ко-

ординаты)

имеющие

этой области непрерывные производные

порядка

не ниже первого.

Область

может быть как неограниченной, так

ограничен-

ной.

случае, когда переменные величины х,

имеют конкретный

биологический смысл (концентрации веществ, численность вида),

На

них, как правило, накладываются некоторые ограничения. Пре-

жде всего, биологические переменные не

могут

быть отрицатель-

ными.

Так

модели Вольтерра, описывающей взаимодействие

Двух

видов, хищника

жертвы,

х^О

— переменная, характеризу-

ющая численность жертвы,

у^-0—хищника. Область

пред-

ставляет собой положительный квадрант правой полуплоскости:

0<х<оо,

0<г/<оо.

Часто численность того или иного вида может быть ограничена

сверху

какими-нибудь внешними по отношению к рассматриваемой

системе условиями, например площадью ареала обитания. В этом

случае

область изменения численности

будет

ограничена

сверху:

0<х<х

О<у<У

Такая

ситуация имела место в

случае

размножения однородной

популяции в ограниченной

среде

(см. уравнение логистической

кривой

во второй главе).

Иногда бывает, что значения переменных (численность вида)

не

могут

упасть ниже определенной величины. Так, для модели

размножения видов нарушение этого означало бы, что вероятность

встречи

двух

особей противоположного пола становится настолько

малой, что размножение невозможно. В этом

случае

область изме-

нения

переменных ограничена не только

сверху,

но и снизу:

го "^

го>

Ую<У<

Уго-

То же имеет место в химической кинетике. Если х и у —

концен-

трации реагирующих веществ, то

0<х<х

0<У<у

где Хо, г/о— максимально возможные концентрации реагентов. Та-

ким

образом, в данном

случае

область G является ограниченной.

В процессе изменения состояния системы во времени перемен-

ные х, у изменяются согласно системе уравнений

(1.3—1)

так, что

каждому состоянию системы

соответствует

определенная пара зна-

чений

неизвестных х, у. Обратно, каждая пара значений (х, у)

описывает определенное состояние системы. Рассмотрим теперь

плоскость с осями координат, на которых отложены значения пе-

ременных х, у. Каждая точка М этой плоскости с координатами

(х,

у)

соответствует

определенному состоянию системы. Как мы

говорили в

главе

1, такая плоскость носит название

фазовой,

или

плоскости состояний системы. Она представляет совокупность

всех

возможных состояний нашей системы. Точка М(х, у) называется

изображающей,

или

представляющей,

точкой. Пусть при t = t

ко-

ординаты изображающей точки М

(хо, г/о)- В каждый следующий

момент времени t изображающая точка

будет

смещаться и при-

нимать положение М(х, у), соответствующее значениям x(t), y(t).

Совокупность этих точек М(х, у) на фазовой плоскости (х, у),

положение которых

соответствует

состояниям системы в процессе

изменения

согласно уравнениям (1.3—1), называется фазовой

траекторией.

Как

мы увидим ниже, характер фазовых траекторий отражает

общие качественные черты поведения системы во времени. Фазо-