Розенберг Л.Д. Физика и техника мощного ультразвука. Книга 1. Источники мощного ультразвука OCR
Подождите немного. Документ загружается.


ми
потерями
в
эпоксидной
смоле
и
неоптимальным
числом
витков
обмот
ки
объяснтотся
небольшие
амплитуды
колебаний,
полученные
на
иссле
дованных
электродинамических
преобразователях.
Однако
исследован
ные макеты
показали
весьма
надежнуЮ
работу.
Рис.
11.
Общий
вид
ЭЛeI{тродинамичеСIl:ОГО
крутильного
преобразователя,
установленного
между
полюсами
магнита
По
результатам
проведенных
экспериментов
можно
сделать
вывод,
что
рассмотренные
модели
достаточно
надежны
и
их
можно
принять
за
ос
нову
для
разработни
систем,
пригодных для
практического
иСпользова
ния.
§
8.
Дисковый
кр
УТИe!lЬВЫЙ
преобрааовате.!lЬ
Недавно
был
предложен
новый
тип
нрутильного
преобразователя
в
виде
плоского
диска
[29],
в
известной
степени
аналогичный
пакетному
преобразователю
Ланжевена.
Дисковый
преобразователь
показан
на
рис.
12
(здесь
1
и
2 -
пассив
ные
металлические
обкладни,
3 -
пьезокерамические
активные
элемен
ты,
из
которых
набрано
кольцо,
R
0-
внешний
радиус
диска,
l -
ширина
кольца,
r
1
-
радиус
внутреннего
ди-
l R
o
ска,
r
o
= r
1
+
]).
Элементы
кольца
поляризованы
таким
образом,
что
после
подачи
электрического
напряжения
на
его
обкладни
в
кольце
возникают
сдви
говые
механические
напряжения
и
в
дисне
возбуждаются
крутильные
коле
бания,
поляризованные
в
его
плоскости.
Технология
изготовления
дискового
z
преооразователя
относительно
неслож-
Рис.
12.
Эсниз
дискового
крутиль
на.
На
торцы
элементов
3
наносятся
ного
преобразователя
обкладки
для
поляризации.
После
по-
ляризации
обкладни
механически
удаляются
и
путем
напыления
в
вакуумо
на
внутреннюю
и
внешнюю
боновые
поверхности
элемента
наносятся
уже
рабочие
обкладки.
Из
подготовленных
таким
образом
эле
ментов
снлепвается
кольцо,
которое
помещается
между
обнладками
1
и
2.
301.

Каждая
из
них
электрически
соединена
с
соответствующей
обкладкой
керамического
кольца.
Электрическое
напряжение
подается
через
выво
ды,
присоединенные
к
обкладкам.
Распределение
амплитуд
крутильных
колебаний
в
диске
и",
(r)
нахо
дится
из
решения
соответствующего
волнового
уравнения.
Это
урав
нение
получается
из
уравнения
(10)
подстановкой
и",
=
r·
q:>
(r).
Когда
q>
=
q>
(r).
e
joot
,
т.
е.
в
диске
установились
синусоидальные
колебания,
уравнение
крутильных
колебаний
в
диске
имеет
вид
1
q/' + 3
<р'
+
k2q:>
=
о.
r
(36)
Чтобы
определить
характерные
размеры
преобразователя
(R
о'
r
o
, l)
и
прежде
всего
его
внешний
радиус
R
о'
необходимо
задать
его
рабочую
частоту
00.
Тогда
по
корням
уравнения
для
собственных
частот
находится
величина
R
о.
Для
получения
уравнения
собственных
частот
задается
условие
отсут
ствия
сдвиговых
напряжений
на
внешнем
крае
диска,
т.
е.
т:
(R
o
)
=
о.
(37)
в
выражение
для
и",
(r)
входит
линейная
комбинация
функций
Бес
селя
и
НеЙмана.
Функция
Неймана
имеет
бесконечную
особенность
при
r =
О.
Физически
очевидно,
что
эту
особенность
необходимо
исключить,
положив
константу
при
функции
Неймана
(111'
см.
ниже)
равной
нулю.
Если
считать,
что
диск
сделан
из
однородного
материала,
т.
е.
не
учиты
вать
неоднородность,В
виде
пьезокерамического
кольца,
то
при
указан
ных
условиях
получается
следующее
уравнение
для
собственных
частот
диска:
(38)
Ниже
будет
ПОI<азано,
что
и
С
учетом
механических
потерь
в
преобразова
теле
допустимо
полагать
в
выражении
(38) k
o
=
ОО/С
нр
•
Из
уравнения
(38)
находятся
первые
три
корня
[24],
соответствующие
первым
трем
модам
колебаний
диска:
koR
o
= 5,13, 8,41, 11,62.
(39)
Отсюда
по
заданному
k
o
находятся
величины
R
о'
Из
них
выбирается
опре
деленное
значение
R
о'
такое,
чтобы
размер
дискового
преобразователя
соответствовал,
например,
размерам
крутильного
концентратора,
присо
единяемого
к
преобразователю.
Амплитуда
крутильных
колебаний,
которую
может
обеспечить
преоб
разователь
при
выбранном
R
о'
естественно,
зависит
от
положения
пьез
0-
керамического
кольца
в
диске
(от
величины
r
o
),
ширины
кольца
l
и
харак
теристик
пьезокерамики.
Зависимость
амплитуды
крутильных
колеба
нпй
от
указанных
величин
определяется
следующим
образом.
Прежде
всего
необходимо
учесть
механические
потери
в
преобразова
теле.
Тогда
выражение
для
волнового
числа
записывается
в
комплексной
форме:
k = k
o
+
ja,
(40)
где
(Х
-
коэффициент
механических
потерь,
принимае:м:ый
одинаковым
для
металла
и
керамики.
Далее
полагаем,
что
(41)
1
Наглядный
вывод
уравнеНIIЯ
(36)
приведен
в
гл.
4,
§ 1.
Отметим,
что
волновое
уравнение
дЛЯ
RРУТИЛЬНЫХ
нолебаний
в
пьеЗОRераМИRе
с
учетом
пьезоэффеRта
не
отли
чается
от
обычного
[30].
302

от:куда
следует
(42)
Из
решения
уравнения
(36)
с
учетом
потерь
находятся
функции
распре
деления
смещений
и",
(г)
для
внутреннего
диска,
пъезокерамического
коль
ца
и
внешнего
кольца.
Эти
функции
в
общем
виде
(см.
гл.
4, § 2),
будут
U1.2,з
=
А
1
•
2
,з
·J
1
(kr)
+
В
1
,2,з
·N
1
(kr).
(43)
Здесь
по
указанным
выше
соображениям
Е
1
=
о.
Затем
для
преобразователя
должны
удовлетворяться
условия
непре
рывности
смещений
на
внутреннем
и
внешнем
краях
пьезокерамического
кольца
(i:i
1
=
и
2
и
и
2
=
uз),
условия
непрерывности
сдвиговых
напряже
ний
в
диске
с
учетом пьезоэффекта
в
кольце
из
пьезоэлектрика
и
условие
отсутствия
напряжений
на
свободном
крае
диска
(r = R
o
).
Эти
граничные
условия
записываются
в
следующем
виде:
~
~
дuз(krо+kl)
--
d
Е
+
ди2
(kro
+kl)
•
и1
(kro) =
и2
(kro);
J.t
ar
- 15ft
J.t
ar
'
дuз(kR
о
)
_
о·
ar
-,
(44)
здесь
d
15
-
пьезоэлектрический
модуль;
Е
-
напряженность
электриче
CI{OrO
поля
в
пьезокерамике;
!-t
-
модуль
сдвига,
который для
упрощения
расчета
полагаем
одинаковым
для
керамики
и
металла.
Подстановка
вы
ражений
(43)
в
граничные
условия
(44)
приводит
к
системе
из
пяти
урав
нений
с
пятью
неизвестными:...4
l'
...4
2'
...4
з,
lJ
2'
lJ
з.
Эти
величины
входят
в
выражения
для
смещений
в
диске
'И
1
,
и
2
и
U
3.
Считая,
что
функция
и
1
=A--;:J
1
(kr)
дает
OCH~BHO~
вклад
в
выражение
для амплитуд
смещений
вди
ске
по
сравнению
с
и
2 и
и
з,
разрешаем
полученную
систему
путем
доста
точно
громоздких
преобразований
именно
относительно
...41.
Функция
J
1
(1;;'),
как
известно
[11],-
затухающая,
и
ее
первый
наибольшиймакси
мум
(он
составляет
--
0,6
и
превосходит
максимальные
значения
функций
Бесселя
и
Неймана,
входящих
в
выражения
для
и
2
и
из),
а
следовательно,
и
максимум
амплитуды
смещений,
которую
обеспечивает
преобразователь,
соответствует
значению
координаты
1 r = r',
такой,
что
I
kl
r' = 2 [24]
(п
р
и
I
тс
I r' = 2, J 1
(1
k 1 r')
~
0,6).
Решение
системы
относительно
...41
приводит
К
следующему
выраже
нию
для
комплексной
«амплитуды}):
~
nd
15
E
{N2
(koR
o
+ ja,R
o
)
<'-'
~
r-'
~ ~
~
А
1 = 2
(k
o
+
ja,)
J
2
(koR
o
+ ja,R
o
)
[(
kr
o
+
kl)·
J
1
(kr()
+ kl) -
kr
OJ
1
(kro)] -
-[(kr
o
+
kZ)
N
1
(kro +
kZ)
-
kr
o
N
1
(kr
o
)]}
(45)
Из
выражения
(45)
следует,
что
1...411
достигает
максимального
значе
ния
при
резонансе,
т.
е.
при
условии
J
2
(k
o
H
o
+ jaHoJ
=miп.
(46)
Из
выражения
(46)
при
условии
(42)
получаем,
как
было
указано
выше,
выражение
(38)
для
собственных
частот.
1
Координата
r'
определяет
радиус
окружности,
находящейся
внутри
nepBoro
диска
радиуса
ro.
По-видимому,
следует
присоединять
крутильный
!,онцентратор
!{
ди
сковому
преобразователю
там,
где
амплитуда
смещений
МaI{симальна,
т.
е.
по
о!\руж
ности
радиуса
r'.
303

Чтобы
найти
I
А
1
1тах,
функции
Бесселя
и
Неймана,
входящие
в
выра
жение
(45),
раскладываются
в
ряд
Тэйлора
по
малому
параметру
а.,то
[см.
условие
(41)].
Малость
этого
параметра
позволяет
отбросить
члены
второго
порядка
по
аг
о
.
Производя
ряд
преобразований,
получаем
для
максимальной
величины
модуля
комплексной
<<амплитуды»
1
Аllтах=Аlтах
(т.
е.
при
резонансе)
следующее
выражение:
А
=~
d
1S
E N
2
(koR
o
)
[(k
r + kol ) J
(k(
r + kol ) _
lтах
2
cl
(k R )
J'
k R )
()
о
2 1 )
О
2
о о
2(
о
()
-
-
(kor
o
-
k~
) J 1
(kor()
-
k~
) ] . (47)
Используя
общее
решение
(45),
получаем
выражение
для
изменения
А
1
по
отношению
к
максимальной
величине
А
1
тах
при
расстройке
относитель
но
резонансной
частоты
10:
где
,
2лj'
k
o
= -
и
l'
</0'
Сир
При
малых
отклонениях
от
резонансной
частоты
и
при
получаем
окончательное
выражение
для
относительных
изменений
«ам
плитуды>>
А
1
крутильного
диска
при
расстройке
частоты:
Аl
1
А
1тах
-
-У1
+4Q2(1-r)2
•
в
выражении
(47)
удобно
привести
левую
часть
R
безразмерному
виду
К
=
2A
1
Cl
= N
2
(k?R
o
)
[(k
r + kol ) J
(k')r
+ kol ) _
лd
1s
Е
(k
R ) J
(k
R )
о
()
2 1
О
2
о
о
2
О
О
-
(kor()
-
k~
) J
1
(kor
o
-
k~l
) ] •
(47а)
Здесь
левая
часть
характеризует
эффективность
преобразователя,
по
скольку
в
нее
входит
отношение
развиваемой
преобразователем
<<аМПЛИТУДЫ»
колебаниii
А
1
к
напряженности
подаваемого
на
преобразователь
электри
ческого
поля
Е.
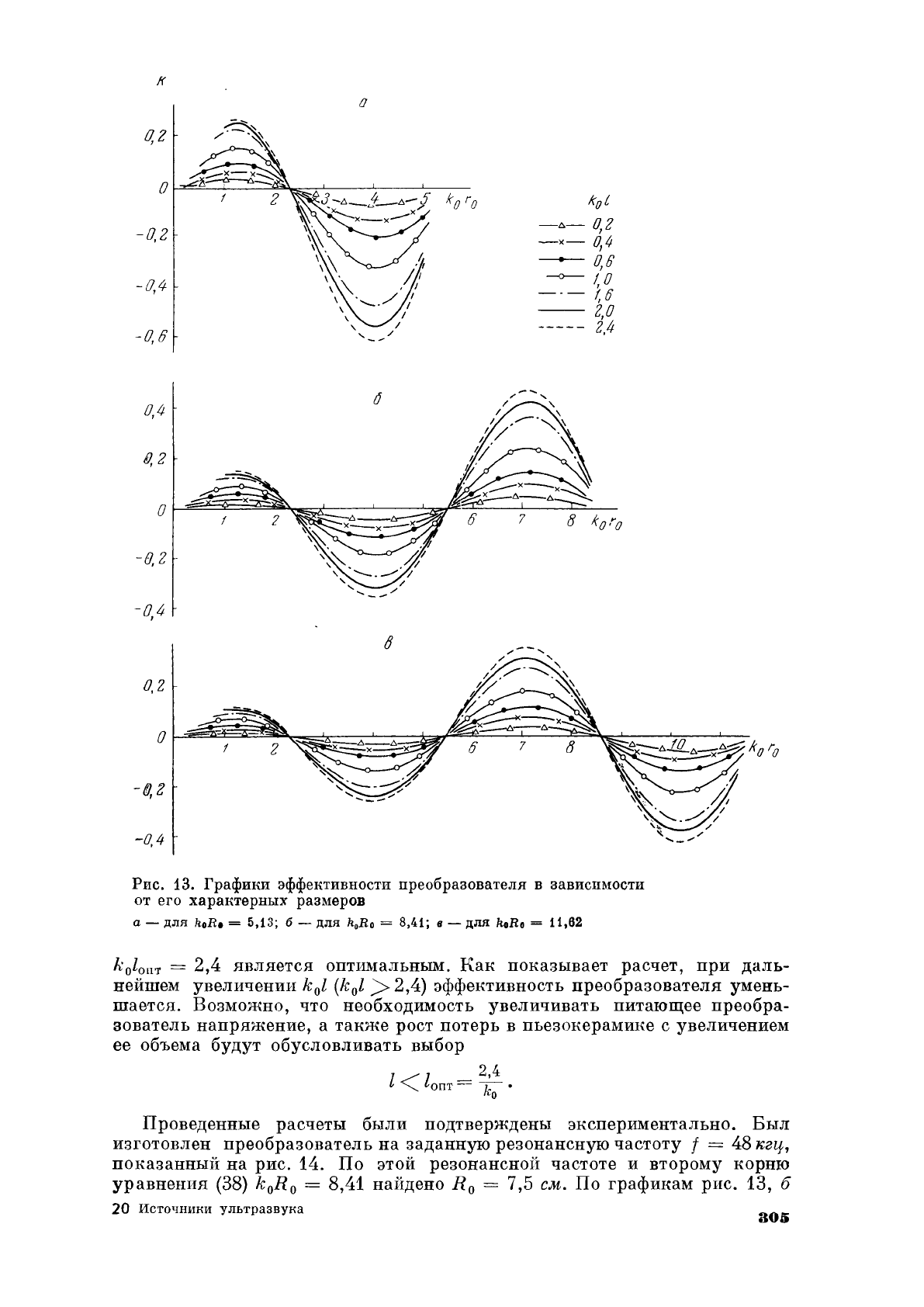
Результаты
численных
расчетов,
проведенных
по
выра
жению
(47а),
представлены
на
графиках
рис.
131.
Графики
построены
для
первых
трех
корней
уравнения
(38)
в
зависимости
от
безразмерной
вели
чины
kor
o
,
которая
при
заданном
k
o
определяет
положение
пьезокерами
ческого
кольца
в
диске.
Параметром
кривых
является
величина
kol.
Анализ
графиков
и
выражения
(47а)
показывает
следующее.
1.
Максимальная
эффективность
преобразователя
достигается
для
первого
корня
уравнения
(38)
koR
o
= 5,13
(при
kor
o
= 4,
К
= 0,6).
2.
Максимальная
эффективность
достигается
при
условии,
что
пьезо
керамическое
кольцо
расположено
вблизи
узла
колебательных
смеще
ний
(например,
при
kor
o
=
1,2,
4,0 -
см.
рис.
13,
а).
3.
С
увеличением
ширины
активного
слоя
l
эффективность
преобра
зователя
возрастает.
Однако
она
возрастает
не
безгранично,
и
значение
1
Численные
расчеты
выполнены
лаборантом
А.
И.
Агеевой.
304:
/(
0,4
!J,2
О
-о.
2
-0,4
0,2
О
-@,г
-0.4
о
tJ
8
7
kot
-д-
0,2
-х-
0,4
---
0,8
-о--
/0
i,б
2,0
-----
2,4
Рис.
13.
Графики
эффективности
преобразователя
в
зависимости
от
его
характерных
размеров
а
-
для
koR.
= 5,13;
б
-
для
koRo = 8,41;
в
-
для
koRo
= 11,62
kol
ollT
=
2,4
является
оптимальным.
Как
показывает
расчет,
при
даль
нейшем
увеличении
kol
(kol > 2,4)
эффективность
преобразователя
умень
шается.
Возможно,
что
необходимость
увеличивать
питающее
преобра
зователь
напряжение,
а
также
рост
потерь
в
пьезокерамике
с
увеличением
ее
объема
будут
обусловливать
выбор
l <
lопт=
~:
•
п
роведенные
расчеты
были
подтверждены
экспериментально.
Был
изготовлен
преобразователь
на
заданную
резонансную
частоту
f = 48
кгц,
показанный
на
рис.
14.
По
этой
резонансной
частоте
и
второму
корню
уравнения
(38)
koR
o
= 8,41
найдено
R
o
= 7,5
см.
ПО
графикам
рис.
13,
б
20
ИСТОЧНИRИ
ультраЗВУRа
305

выбирается
значение
kor
o
= 3,83,
т.
е.
r
o
~
3,8
сж.
Ширина
пьезокера
МИ1l{еского
кольца
l
выбрана
равной
0,8
см,
что
соответствует
значению
kol = 1.
При
экспериментальном
испытании
преобразователя
электрическое
напряжение
подавал
ось
от
генератора
3Г-12,
причем
обеспечивалось
поле
100
в/см.
С
помощью
датчика
ускорений,
приклеенного
к
своБОД4
ному
краю
преобразователя,
определялись
его
резонансные
частоты.
Основная
резонансная
частота
47
1l:гц
хорошо
соответствует
заданной
час
тоте.
Обнаружен
также
резонанс
на
частоте
около
30
1l:гц,
что
соответствует
первому
корню
уравнения
(38).
Определенная
по
резонансной
кривой
Рис.
14.
Дисковый
крутильный
преобразователь
преобразователя
добротность
Q
составила
-... 280
и
соответственно
коэф
фициент
потерь
CJ.
=
QЛ!
= 0,0017
с.ч-
1
.
Таким
образом,
условие
(41)
С
нр
было
выполнено.
По
выражению
(47)
с
использованием
известных
уже
величин
R", r
o
,
l,
Е,
а,
d
15
определена
«амплитудю>
A
1
= 2,3 M1l:
(при
r = r').
Поскольку
поляризация
элементов
кольца
производилась
при
пониженном
напряже
нии,
величина
A
1
должна
быть
скорректирована
с
учетом
того
обстоятель
ства,
что
d
15
составлял
не
250·10-
1и
см/в,
а
около
150·10-10
см/в.
Тогда
A
1
составит
1,4
M1l:.
Амплитуда
колебаний
определялась
эксперименталь
но
на
расстоянии
r =
r'
от
центра
диска
по
размытию
освещенных
точек
в
поле
зрения
микроскопа.
Величины
размытий
порядка
единиц
микрон
находятся
на
пределе
разрешающей
способности
микроскопа.
Однако
раз
мытие
обнаруживалось,
и
это
позволяет
считать,
что
амплитуда
колеба
ний
преобразователя
по
порядку
величины
соответствует
расчетной.
По
результатам
проведенных
исследований
дискового
крутильного
преобразователя
можно
сделать
вывод,
что расчет
таких
преобразовате
лей
можно
производить,
используя
выражения
(38)
и
(47)
и
графики
рис.
13.
Преобразователь
обеспечивает
достаточную
амплитуду
колебаниii
для
возбуждения
технологичеСI<.IIХ
крутильных
колебательных
систем.
Специального
сопоставления
преобразователя,
рассмотренного
здесь
и
в
предыдущем
пара
графе
(см.
рис.
6),
не
проводилось.
Дисковый
преоб
разователь,
по-видимому,
более
прпспособлен
для
возбуждения
концент
раторов
типа
«трепаю>,
тогда
как
цилиндрический
преобразователь
со
специальными
обкладками
СЕорее
пригоден
для
возбуждения
сплошных
концентраторов.
806

Гаава
3
СТЕРЖНЕВЫЕ
RРJ7ТИ.JIЬНЫЕ
КОНЦЕНТРА.ТОРЫ
В
этой
главе
на
основе
решения
волнового
уравнения
для
нрутильных
нолебаний
неоднородного
стержня
дается
ряд
соотношений,
необходимых
для
прантических
расчетов
при
конструировании
стержневых
крутильных
концентраторов.
§ 1..
Расчет
ВРУТИ.J.Iьных
концентраторов
Нак
было
показано
в
гл.
1,
уравнение
для
крутильных
колебаний
стержня
переменного
сечения
(неоднородный
стержень)
можно
записать
в
виде
(48)
где
<Рl
-
угол
поворота
сечения;
р
и
J.t
-
плотность
и
модуль
сдвига
ма
териала
стержня;
1
р
(х)
-
полярный
момент
инерции
поперечного
сече
ния
стержня.
Нужно
только
не
забывать,
что
уравнение
(48)
выведено
в
предполо
жении,
что
при
колебаниях
стержня
его
сечения
поворачиваются
как
це
лое,
не
искажаясь.
В
крутильных
концентраторах
это
условие
может
на
рушаться,
так
как
могут
возникнуть
колебания
сложной
формы,
для
ко
торых
уравнение
(48)
неприменимо.
Нак
следует
из
изложенного
в
гл.
1,
даже
для
однородного
стержня
волновое
уравнение
для
гармонических
волн
в
случае
искажения
сечений
будет
существенно
сложнее,
чем
урав
нение
(48)
[см.
выражение
(16)].
Однако
при
практических
расчетах
все
же
можно
применять
уравнение
(48),
имея
ввиду,
что
в
выполненном
в
материале
концентраторе
при
его
возбуждении
принципиально
можно
ожидать
возникновения
сложных
крутильных
колебаний
(типа
колебаний
с
узловыми
цилиндрами).
Второе
обстоятельство,
на
которое
следует
обратить
внимание,
состо
ит
в
том,
что
если
крутильный
вибратор
обеспечивает
не
чисто
крутиль
ное
возбуждение
концентратора,
в
последнем
могут
ВОЗНIшнуть
другие
колебания
кроме
крутильных.
Найдем
решение
уравнения
(48)
для
случая
<рl
=
<pe
jcut
, (49)
т.
е.
полагая,
что
в
стержне
установились
синусоидальные
колебания.
Подставляя
(49)
в
(48),
получим
где
1 81
(х)
<р"
+
--
_Р_<р'
+ k
2
<p
=
О,
lр
(х)
8х
(J)
=
2л:f.
(50)
Уравне-ние
(38)
получено
без
учета
механических
потерь
в
материале
кон
центратора.
Между
тем
при
выборе
слишком
больших
коэффициентов
усиления
может
происходить
разогрев
и
даже
разрушение
концентратора
в
зоне
пучности
деформаций.
Чтобы
этого
не
случилось,
необходимо,
используя
выведенные
ниже
соотношения
длл
распределения
крутиль
ных
деформаций,
определять
величину
максимальных
напряжений
в
кон-
20*
307

центраторе
по
заданной
величине
угла
закручивания
~o
на
его
входе.
Величина
максимальных
напряжений
сравнивается
с
пределом
устало
сти
металла,
из
которого
выполнен
концентратор,
при
динамическом
на
гружении.
Если
окажется,
что
величина
напряжений
превосходит
предел
усталости,
величина
~o
должна
быть
уменьшена.
Аналитический
учет
потерь
сталкивается
со
значительными
трудно
стями,
так
как
требует
введения
новых
членов
в
волновое
уравнение.
Однако
в
некоторых
частных
случаях
могут
быть
использованы
упроща
ющие
приемы,
аналогичные
тем,
которые
применяются
в
§ 12, 14, 15
ра
боты
[19]
для
концентраторов
продольных
колебаний.
о
:r
Q
Рис.
15.
Крутильные
концентраторы
о
:с
о
г
а
-
нонцентратор
специальной
формы
[т
=
Тl
chy(l
-
х)],
ПУНRТИРОМ
ПОRазана
исследованная
форма
т
= Tl V
chy(l
-
х);
б-
-
нонцентратор
ЗRСПО
ненциальной
формы;
в,
г
-
ступенчатые
нонцентраторы
Решим
уравнение
(50)
для
концентратора
специальной
формы,
no-
казанного
пунктиром
на
рис.
15,
а
1:
r = r 1 V
c-=h-y-(-:7
l
-=--x--:-),
(
51
)
где
у=
+ArchN2,
(52)
причем
N = r
O/rl
и
r
о'
rl
-
соответственно
радиусы
входного
и
выходного
сечения концентратора,
а
l -
его
длина.
Для
полярного
момента
инер
ции
и
aI~;x)
= _
~
rtychy(l-x)shy(l-
х).
Подставляя
(53)
и
(54)
в
уравнение
(50),
получим
~"-
2у
th
у
(l-
x)~'
+
k2~
=
о.
(53)
(54)
(55)
Зададим
граничные
условия.
Для
узкого
конца
стержня
(х
= l)
при
от
сутствии
нагрузки
дер
(l)
_
О
дх
- .
(56)
1
Поскольку
имеется
формальное
сходство
между
волновыми
уравнениями
для
продольных
и
крутильных
концентраторов,
расчеты,
изложенные
ниже,
ПРОВОДИЛIlСЪ
согласно
методике,
приведенной
в
работе
[20J.
Общий
анализ
уравнения
для
крутильных
концентраторов
дан
в
работе
[31].
Концентратор
с
зависимостью
r =
rl
V
сЬ
l'
(l
-
х)
предложен
А.
В.
кулемины
•.
308

Если
считать,
что
широний
нонец
стержня
(х
=
О)
присоединен
н
резо
нансному
нрутильному
преобраЗ0вателю,
то
условие
идеального
согла
сования
будет
иметь
вид
д<р
(О)
=
о.
дх
(57)
Стержень,
рассчитанный
при
условиях
(56)
и
(57),
является
резонансным,
и
присоединение
его
н
преобразователю
не
изменит
режима
работы
по
следнего.
Поэтому
(58)
где
СРо
-
угол
занручивания
на
нонце
преобразователя.
Решение
уравне
ния
(55)
дает
<р
=
ch
i
(~_
х)
(А
1
cos k'
х
+
А
2
sin
k'
х),
где
(59)
а
А
1
И
А
2 -
произвольные
постоянные,
ноторые
находятся
с
учетом
ус
ловий
(56)
и
(57).
Выражение
(59)
определяет
дисперсионную
зависимость
фазов{)й
сно
рости
нрутильных
нолебаний
в
зависимости
от
ноэффициента
у,
харанте
ризующего
нрутизну
сужения
нонцентратора.
Легно
поназать,
что
,
эта
снорость
С
кр
превышает
значение
снорости
в
стержне
постоянного
сечения
С
кр
•
Действительно,
подставляя
k'
=
Ю/С~р
в
выражение
(59)
и
производя
простые
преобразования,
получим
(60)
Отсюда
очевидно,
что
существует
неноторая
нритичесная
частота
таная,
что
нолебания
частотой
ниже
ffi
крит
не
могут
распространяться
в
нон
центраторе.
Поснольну
величина
у,
нан
будет
поназано
ниже,
входит
в
выражение
для
ноэффициента
усиления
нонцентратора,
то
совершенно
ясно,
что
для
любой
заданной
ffiраб
>
ffi
крит
будет
существовать
предельная
величина
усиления,
зависящая
от
Упр,
ноторую
можно
получить,
исполь
зуя
рассматриваемый
нонцентратор.
Принимая,
согласно работе
[19],
(61)
имеем
Упр
= (1,5
-7
2)
С
кр
(62)
[см.
выражение
(65)].
Для
постоянных
А
1
И
А
2
получаем
А
2 =
А
1
tg
k'
l,
А
2
= -
А
1
Z,
thyl,
отнуда
следует,
что
основное
соотношение
для
резонансных
значений
k'
l
(дисперсионное
уравнение)
для
рассматриваемого
нонцентратора
с
309

учетом
(52)
будет
k'ltgk'l
=
-АrсhN2
V
1-~4
,
а
распределение
углов
закручивания
вдоль
концентратора
q>=q>ОСh;~l~Ж)
(cosk'Z-
1.
thy1sink'x).
(63)
(64)
Из
соотношения
(64)
находим
коэффициент
усиления
по
углу закручивания
I
<pl
I
N2
К
- -
---
ер
-
<ро
- cos
k'
1 •
(65)
Напомним,
что
N2
=
ch-y1
[см.
выражение
(52»).
Коэффициент
усиления
по
линейным
смещениям
на
поверхности
концентратора
равен
к
_\_<pl_·r
l
/
__
N..,....,...,...
лин
-
<po.ro
- cos
k'l
•
(66)
Используя
выражения
(52)
и
(59),
а
также
k
==
2
п/л,
получаем
выраЖQ
вие
для
резонансной
длины
концентратора:
(67)
где
k'
1 -
корни
дисперсионного
уравнения
(63),
которые
находятся
чис
ленным
методом.
Представляет
практический
интерес
нахождение
координаты
Х/ер=о,
соответствующей
<р
(Х)
=
О,
как
возможного
места
присоединения
к
кон
центратору
элементов
крепления
(опорных
изоляторов).
Из
выражения
(64)
имеем
1 (
k'
)
Х
\ер=о
=
k'
arctg
r
cth
y1
•
(68)
Распределение
угловых
деформаций
вдоль
концентратора
получим,
дифференцируя
выражение
(64):
<р'(х)
=
-q>ОСhii~~'::ж)[thу(l-
x)(cosk'x.-
Z,
thylsink'x)
+
+
(~
sin
k'
Х
+
th
y1
cos k'
Х)
] ' (69)
откуда,
приравнивая производную
от
(69)
нулю,
получаем
выражение
для
координаты
пучности
угловых
деформаций
Х/ер"=о
= X
1
[(
~Y-cth22y(1-
Xl)](cosk'Xl-
1.
thy1sin
k'Xl) =
(
k'
= 2
th
у
(1-
Xl)
r
sin
k'
Xl
+
th
yl
cosk'
Xl)
•
(70)
Величины
k',
у,
1
могут
быть
вычислены
на
основании
предыдущих
рас
четов,
и,
следовательно,
численное
нахождение
X
1
по
выражению
(70)
не
представит
особых
затруднений.
Поскольку
в
конечном
счете
требуется
найти
величину
максимальных
деформаций
в
концентраторе,
можно
ре
комендовать
другой
путь.
При
работе
изготовленного
согласно
расчету
концентратора
экспериментально находят
величину
X
1
и
после
подстанов
ки
ее
в
выражение
(69)
получают
величину
максимальных
деформаций,
а
затем
и
напряжений
в
концентраторе.
31..0
