Романовский С.И. Седиментологические основы литологии

Подождите немного. Документ загружается.

Авторы

рассмотренных в этой главе моделей (А. Б. Вистелиус,

К.

И. Хейсканен и А. В. Вихерт) опирались в своей работе на

конкретный фактический материал по

единичным

в генетическом

отношении типам отложений и, естественно, в рамках статических

моделей пришли к вероятностным схемам слоенакопления

раз-

ного типа.

ГЛАВА

МОДЕЛЬ СЛОЕНАКОПЛЕНИЯ А. Н. КОЛМОГОРОВА

ИСХОДНЫЕ

ПРЕДПОСЫЛКИ

И ФОРМАЛЬНАЯ ТРАКТОВКА ПРОЦЕССА

Как было показано в предыдущей главе, существуют 2 подхода

к объяснению условий формирования слоистости осадочных отло-

жений: тектонический, с помощью которого главным образом

удается реконструировать закономерности в образовании осцил-

ляционно-миграционной слоистости, и седиментологический, да-

ющий разумную интерпретацию условий, приводящих к формиро-

ванию слоистости мутационного типа. Причем вне зависимости

от

того, происходит ли осадконакопление в прибреяшо-морской

зоне или в областях, пограничных с континентальным склоном,

на абиссальных равнинах океанов или в озерных условиях, па

суше

в различных физико-географических обстановках или в рус-

лак рек, выделяют 2 (во многом различных) класса процессов

слоенакопления, которые мы также назовем осцилляционно-

мпграционным и мутационным.

Режим процесса в зависимости от условий его протекания,

как правило, оказывается различным, но эти различия фикси-

руются чаще всего в текстурных особенностях слоев (появление

косослойчатых серий, слоев с градационной слоистостью и т. п.)

или в закономерностях наслоения, которые отражают тектони-

ческие и гидродинамические особенности конкретного в струк-

турно-морфологическом отношении бассейна.

Для наших

целей

представляет интерес выявление тех общих

характеристик процесса слоенакопления, которые в равной мере

укладываются в схему формирования как осцилляционпо-мигра-

ционной,

так и мутационной слоистости. Осцилляционно-мигра-

ционная

слоистость вне зависимости от фациальных условий

образуется

в результате миграций береговой

линии

бассейна

седиментации, управляемых тектоническими

осцилляциями

[40].

При этом предполагается, что при отрицательных двиялепиях

земной коры происходит накопление слоя фиксированного лито-

логического состава, а при полоячительных — размыв. Правда,

размыву

в буквальном смысле может быть подверяхен далеко не

каждый слой, но для нас важным является сам факт сокращения

первоначально накопленной мощности слоя. И не столь суще-

ственно, происходит уменьшение мощности в результате размыва

или уплотнения под действием собственной массы накапливающе-

гося осадка.

Подчеркнем, что в каждый элементарный период слоеобразова-

ния формируется промежуточная мощность £-го слоя. Слой с но-

мером i может быть частично или полностью размыт и спустя

несколько элементарных периодов слоеобразования, но если

этого не произошло, то предполагается, что в дальнейшем i-й слой

не размывается и окончательно закрепляется в разрезе, т. е.

процесс реализует окончательную или зафиксированную мощ-

ность слоя.

При образовании мутационной слоистости (флишевые отложе-

ния, ленточные

глины

и т. д.) геологическая трактовка механизма

слоенакопления в рамках рассматриваемой схемы в основном

не изменяется. По-прежнему кинематика процесса представляется

виде непрерывно сменяющих друг друга во времени этапов

накопления

и размыва слоев, а точнее, этапов

накопления

и после-

дующего сокращения первоначально накопленных мощностей.

Важно

подчеркнуть, что при такой трактовке процесса слое-

накопления

принятая нами схема приложима к анализу законо-

мерностей в наслоении применительно к самым разнообразным

типам стратификации. Тот факт, что механизм собственно нако-

пления

слоя и механизм размыва определяются в конечном счете

фациальными в широком смысле слова условиями и существенно

различны для каждого литогенетического типа отложений, при

рассмотрении данной схемы процесса роли не играет, поскольку

она не предусматривает в изначальной трактовке описание кон-

кретных характеристик механизма слоенакопления.

Лишь при реализации модели, которая в частном случае

может

быть сведена к оценке меры стабильности слоенакопления,

различия в механизме

накопления

и размыва слоев при образова-

нии генетически различных типов отложений оказываются суще-

ственными, ибо ими определяется аппроксимация распределения

промежуточных мощностей слоев конкретной плотностью вероят-

ностей.

Перейдем к формальному описанию данной кинематической

схемы,

для чего необходимо прежде всего определить слоенакопле-

ние как вероятностный процесс. Предварительно заметим, что

вероятностную модель слоенакопления А. Н. Колмогорова [146]

автор

неоднократно использовал для решения разнообразных

геологических задач. Поэтому в данной работе будут обстоятельно

изложены только те результаты, которые получены в процессе

работы над монографией. Результаты, публиковавшиеся ранее,

упоминаются лишь вскользь, а связанные с

ними

формулы будут

приведены без вывода.

Введем

в рассмотрение координатное пространство (А, 51),

по определению Ю. В. Прохорова и Ю. В. Розанова

[217],

где

а множество индексов T будем трактовать как матема-

тический аналог времени. В этом пространстве заданы функ-

ции 8

(h) — промежуточные мощности слоев. Координату б^

фиксированный момент времени t назовем элементарным собы-

тием. Тогда функция б = (h) в пространстве элементарных

событий будет трактоваться как случайная величина, имеющая

функцию распределения G = р (б ^

h).

Таким образом, имеем

семейство случайных величин {6^ (h), t £

T}.

Единичные

I I! I Il I Il

LOJ I LJ ! I 1

Sf tfSi t2 Sj tj tn-, Sn t

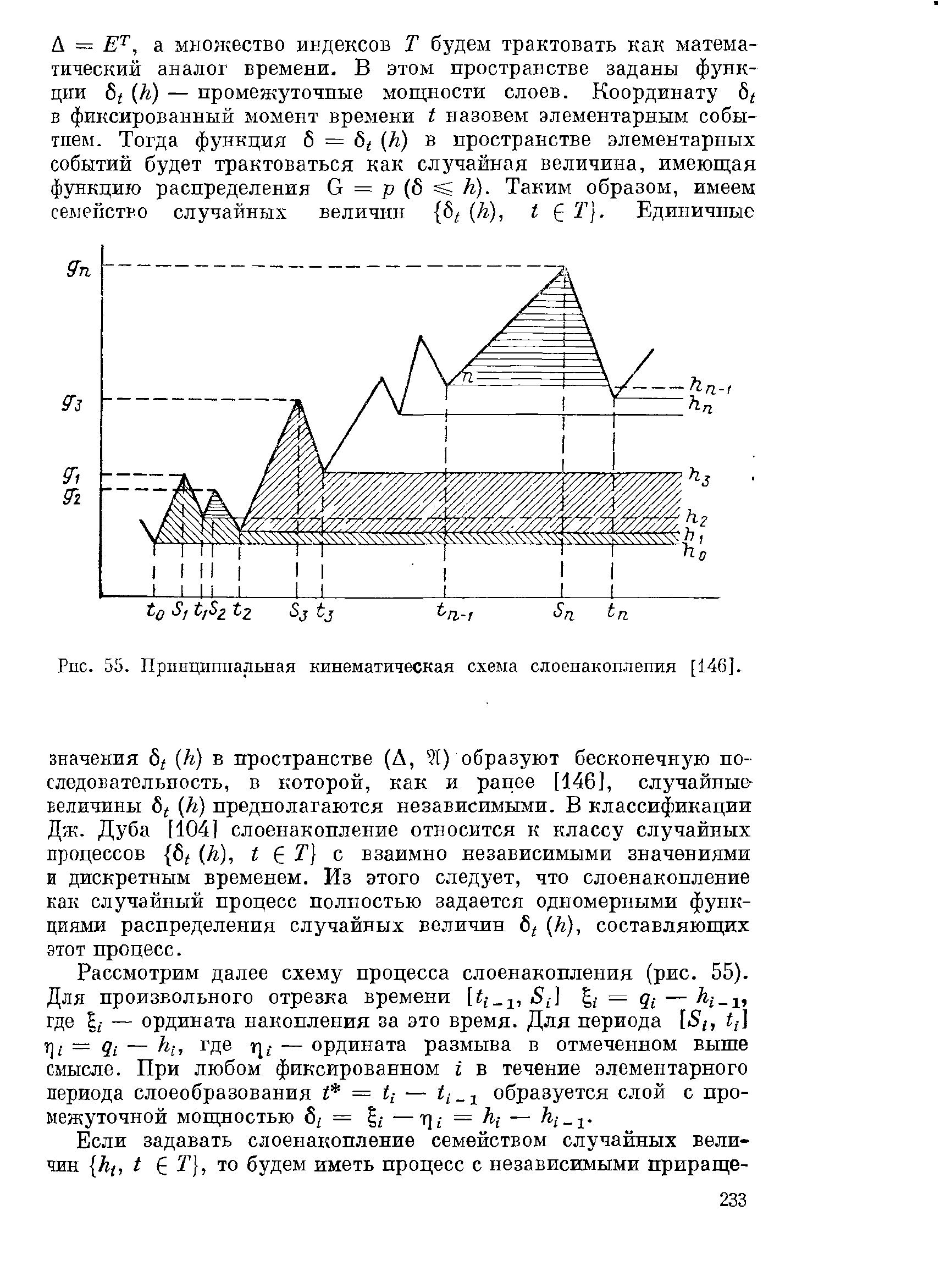
Рнс. 55. Принципиальная кинематическая схема слоенакоплепия

[146].

значения (Ji) в пространстве (А, 91) образуют бесконечную по-

следовательность, в которой, как и ранее

[146],

случайные

величины б^

(Ji)

предполагаются независимыми. В классификации

Дж. Дуба [104] слоенакопление относится к классу случайных

процессов

{6^

(Ji), t £ T] с взаимно независимыми значениями

и дискретным временем. Из этого следует, что слоенакопление

как случайный процесс полностью задается одномерными функ-

циями распределения случайных величин 6^ (h), составляющих

этот

процесс.

Рассмотрим далее схему процесса слоенакопления (рис. 55).

Для произвольного отрезка времени It^

, S

] £

= q

—

где — ордината накопления за это время. Для периода

[Si,

]

T]i

—

hi,

где rjj — ордината размыва в отмеченном выше

смысле.

При любом фиксированном i в течение элементарного

периода слоеобразования t* = t

— ^

-1

образуется слой с про-

межуточной мощностью бi =

—и i = hi —

Если задавать слоенакопление семейством случайных вели-

чин

t £

T},

то будем иметь процесс с независимыми прираще-

ниями,

который легко может быть сведен к процессу с взаимно

независимыми значениями. Действительно,

= H^ + S

;

= ^0 + 6i +

• «.••..•.•.

= h

+ S

+ . . . + б

Получили процесс с независимыми приращениями, а так как

при t

< . . . < t

(п ^ 3) разности h

— h

, . . ., k

— h

взаимно независимы (по предположению, что случайные величины

}T=i

независимы), то имеем процесс с взаимно независимыми

значениями (б^, t £ T].

Сложность более точной классификации слоенакопления как

вероятностного процесса определяется следующими обстоятель-

ствами.

При любом in = t

— t

-\ и фиксированном значении

случайной величины

%t*

промежуточная мощность 8

* в общем

случае определяется не значением случайной величины rw*,

rj/* , где г = 0, 1, . . ., I. Таким образом, для каждого эле-

ментарного периода слоеобразования f

величина промежуточной

мощности 8/* определяется не предшествующим состоянием (пери-

одом

tn_i),

а одним из будущих состояний процесса, т. е. орди-

натой размыва rw*

одном из последующих периодов слое-

образования

При tn+/+i величина размыва

r]n+i+i

уже

не сказывается на значении промея^уточиой мощности б^*.

Имеем случайный процесс, который может быть противопо-

ставлен процессам марковского типа. Насколько известно автору,

процессы такой структуры теорией вероятностей специально

не изучались. Очевидно, что для более строгого задания слое-

накопления как случайного процесса необходимо определить

характер зависимости промежуточных мощностей слоев б^* от

будущих состояний, т. е. значений размывов в последующие

элементарные периоды слоеобразования

Tj/*

Однако кроме

предположения о том, что лишь при конечных и не очень боль-

ших г величина г] еще сказывается на значении промежуточ-

ной мощности бф другимп разумными ограничениями на г];*

геология не располагает. Данное же допущение объясняется

геологической спецификой процесса слоенакопления, которая

заключается в том, что в среднем, т. е. для достаточно больших

отрезков

времени, ординаты

накоплений

преобладают над глу-

бинами размывов Mb

> 0, хотя ясно, что для любого конкрет-

ного периода слоеобразования

может быть и отрицательной

и равной нулю.

Сделаем следующие допущения

[146].

1. Случайные величины б„ взаимно независимы и характери-

зуются

одной и той же функцией распределения вероятностей

<Сх) = G (х). Для нашей цели важно знать распределение

случайных величин I

, т. е. р (^

<^х) = р (х) ит|„, т. е. р (г]

—

Q (х). Тогда распределение случайной величины S

опре-

деляется как

<x)

= p(l

-r]

<:x) = G(x). ' (167)

Процесс слоенакопления полностью задается одномерными функ-

циями распределения G (х). Это следует из свойства независи-

мости

б,

Математическое ожидание случайных величин 8,

положи-

тельно,

т. е.

со

= J xdG(x)>Q. (168)

—

СО

Распределение случайных величин S

непрерывно, т. е.

G(X)=

f g(x)dx. (169)

—

СО

Далее А. Н. Колмогоров рассматривает суммы £„

г)

= S

-f

n+1

+ • • • + б

л+г

, которые согласно второму допущению

при неограниченном возрастании индекса г будут стремиться

-f-oo,

но при любом, зависящем от случая номере г их точные

нияшие грани конечны, т. е.

(

*{Й°\

&\ tf\ ..-}• (ПО)

Таким

образом, получаем последовательность случайных вели-

чин {фя}. Покажем, что ф„ действительно является случайной

величиной. Если {S

, п ^ 1} образуют случайный процесс, то

определение нижней грани приводит к функциям от S

, т. е. к ^

которые также являются случайными величинами, т. е. измери-

мыми функциями. Так, ф

— случайная величина, так как из

равенства

}

СО

U {| (S) KM ' (171)

следует,

что стоящее в его левой части множество точек б является

суммой

счетного числа измеримых множеств, а следовательно,

и само измеримо

[104].

Рассмотрим

2 возможных случая, когда происходит либо пол-

ный, либо частичный размыв слоя. Если ф„ ^ 0, то слой с номе-

ром

п полностью размывается. Пусть, к примеру, ф

= 0. Тогда

Фгг

= inf

(&°>)

= К - h

= 0, (172)

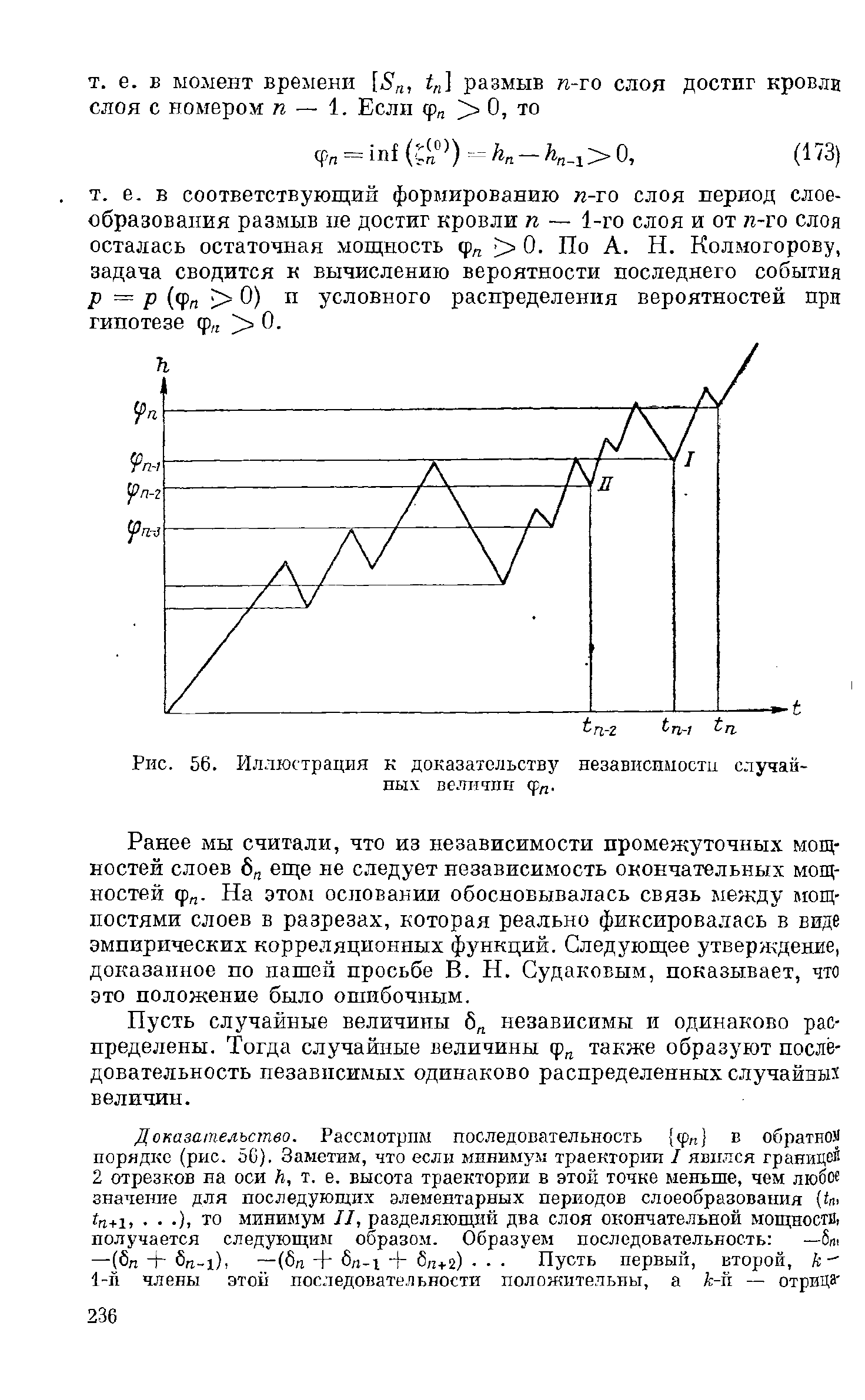
т.

е. в

момент времени

, t

]

размыв п-то слоя достиг кровли

слоя

номером

—

Если

<р„

> 0, то

Фя

= inf

(<:„

)

=К-

K-i>

(173)

т.

е. в

соответствующий формированию гг-го слоя период слое-

образования размыв

не

достиг кровли

—

1-го

слоя

и от

?г-го

слоя

осталась

остаточная мощность

•>

0. По А. Н.

Колмогорову,

задача

сводится

вычислению вероятности последнего события

р=р

(фя j> 0)

условного распределения вероятностей

при

гипотезе

> 0.

Рис.

56.

Иллюстрация

доказательству независимости случай-

ных

величин

Ранее

мы

считали,

что из

независимости промежуточных мощ-

ностей слоев

еще

не

следует независимость окончательных мощ-

ностей фя.

На

этом основании обосновывалась связь между мощ-

ностями слоев

разрезах, которая реально фиксировалась

виде

эмпирических корреляционных

функций.

Следующее утверждение,

доказанное

по

нашей просьбе

В. Н.

Судаковым, показывает,

что

это положение было ошибочным.

Пусть случайные

величины

независимы

одинаково рас-

пределены. Тогда случайные

величины

также образуют после-

довательность независимых одинаково распределенных случайных

величин.

Доказательство. Рассмотрим последовательность

{<p

}

обратном

порядке (рис. 56). Заметим, что если минимум траектории

явился границей

отрезков

на оси h, т. е.

высота траектории

этой точке меньше, чем любое

значение

для

последующих элементарных периодов слоеобразования (fai

• -)i то

минимум

//,

разделяющий

два

слоя окончательной мощности»

получается следующим образом. Образуем последовательность:

—

бш

—(6

+ 6

-i), —

(бп

бя-i

+ 6/2+2) - . .

Пусть первый, второй,

k ^

1-й

члены

этой последовательности положительны,

a k-ii —

отриЦЗ'

те

лен.

Распределение величины ф, ограниченной проекциями вершин / и 77

на ось /г, есть распределение этой первой отрицательной суммы в последова-

тельности: —6

—

(б

+ $n-i) . . . Так как последующая окончательная

мощность

слоя ф определяется аналогично с помощью

величин

6^, не завися-

щих от тех, с помощью которых определялась величина окончательной мощ-

ности предыдущего слоя, то величины ф

/г

сами независимы (и одинаково

распределены). Утверждение доказано.

Существенным недостатком рассматриваемой нами вероятно-

стной схемы процесса слоенакопления является предполон^еиие

о независимости промежуточных мощностей 8

/г

, так как из этого

допущения согласно доказанному утверждению следует и незави-

симость случайных

величин

/г

, т. е. мощностей слоев, оконча-

тельно зафиксированных в разрезе. Однако разумной альтерна-

тивы этому допущению найти не удалось. Предположение о мар-

ковском характере слоенакопления справедливо, когда рассматри-

вается

последовательная смена в разрезе слоев фиксированного

состава

без учета мощностей, да и то далеко не для всех типов

отложений. Для последовательности мощностей слоев (если аб-

страгироваться от состава пород) предпосылки, приводящие

цепи

Маркова, как мы показали в начале данного раздела, не

выполняются в рамках рассматриваемой вероятностной схемы

процесса.

Таким образом, задача будущего — иалоя^ение

ограничений

на тип зависимости промежуточной мощности 8/* от размыва

на Z-м

шаге,

т. е. от

величины

r\t*

не

очень велико. Как

заметил Дж. Дуб [104, с. 49]: «...наименование «вероятностные

процессы»

сохранилось за семействами (обычно бесконечными)

случайных

величин

с некоторыми простыми взаимосвязями менаду

величинами. Одной из основных задач является установление

подходящих классов таких взаимосвязей, т. е. обнаруя^ение

новых типов вероятностных процессов, являющихся полезными

или математически изящными или же вообще каким-либо образом

удовлетворяющих критерию важности, применяемому исследова-

телем».

Подробное описание модели А. Н. Колмогорова и вывод фор-

мул, используемых для расчета вероятности сохранения в разрезе

слоя

конечной

мощности, когда g (х) аппроксимируется различ-

ными

функциями

распределения (нормальной, рэлеевской и экс-

поненциальной), опубликован во многих работах [5, 6, 28, 91,

235,

238, 242, 250, 319]. Поэтому здесь мы их приведем без вывода.

заключение отметим, что ввиду прикладного геологического

характера

задач, решаемых на основе вероятностной схемы слое-

накопления

А. Н. Колмогорова, вычислительные формулы должны

быть без ущерба практически требуемой точности достаточно

простыми, чтобы ими можно было легко воспользоваться как

целью исследования динамических особенностей седиментации

различных стратифицированных отложений, так и для постановки

других задач, связанных с тектоническим и фациальным анализом

мощностей.

ВЕРОЯТНОСТНЫЕ

КРИТЕРИИ СТАБИЛЬНОСТИ СЛОЕНАКОПЛЕНИЯ

вероятностным критерием стабильности слоенакопления мы

относим характеристики, которые можно получить при реализа-

ции модели А. Н. Колмогорова на конкретный

природный

объект.

Как отмечалось, геологическая специфика слоенакопления

отображается в вероятностной схеме процесса таким образом,

что помимо его формальной трактовки появляется возможность

оценивать ряд характеристик, отражающих динамику слоенако-

пления,

и среди них в первую очередь вероятность «окончатель-

ного»

сохранения в разрезе слоя

конечной

мощности р. Большое

значение для развития вероятностной теории слоенакопления

имеет введенная А. Н. Колмогоровым случайная величина 8„,

которую мы называем промежуточной мощностью слоя. Данное

понятие важно в том отношении, что оно в строгом соответствии

вероятностью окончательного сохранения слоя позволяет поста-

вить вопрос и вычислить как суммарную мощность размытых

процессе слоенакопления отложений, так и среднее число

раз-

мытых слоев.

Поскольку предполагается, что значения промежуточных мощ-

ностей 8

взаимно независимы и имеют

один

и тот же закон рас-

пределения, то вероятность окончательного сохранения гг-го слоя

не зависит от номера п. Это позволяет трактовать р как вероятно-

стную характеристику направленности процесса слоенакопления

и считать ее количественной мерой интенсивности седиментологиче-

ского режима бассейна, фиксирующей, например, стабильность

процессов осадконакопления в ходе формирования конкретной

осадочной толщи.

Дадим определение стабильности процессов слоенакопления.

Идеально стабильным режимом слоенакопления будем называть

такой режим, который в каждый элементарный период слоеобразо-

вания фиксирует в разрезе слои равной мощности. Это означает,

что выборочная совокупность мощностей слоев при идеально

стабильном режиме должна иметь дисперсию мощностей, равную

нулю. Поскольку в реальных геологических разрезах дисперсия

мощностей всегда отлична от нуля, то и реальные процессы слое-

накопления

не являются идеально стабильными. Формально

идеально стабильный режим слоенакопления может быть опре-

делен через вероятность окончательного сохранения слоя р.

Если р = 1, то процесс идеально стабильный. Отметим, что на

практике мы всегда имеем дело с р < 1, т. е. реальный процесс

слоенакопления всегда характеризуется некоей (отличной от нуля)

УЧ.

мерой

«размыва»

слоев: 1 — р

Введение меры размыва в сочетании с вероятностью сохране-

ния слоя позволяет восстанавливать размытые суммарные мощ-

ности в анализируемых разрезах и строить гипотетические

раз-

резы,

т. е. такие, какие имели бы место в случае отсутствия факто-

ров,

сокращающих промежуточные мощности слоев. При этом

появляется реальная возможность построить развертку полного

спектра

колебательных движений земной коры, если анализу

подвергается

осцилляционно-миграционная слоистость. Кроме

того,

достаточное количество разрезов одного бассейна седимента-

ции и палеофациальное районирование позволяют получить коли-

чественную оценку степени устойчивости динамической системы

осадконакопления в площадном масштабе для разных фациальных

зон

[91], а также проследить эволюцию седиментологической об-

становки во времени при

наличии

в разрезах синхронных пачек,

различающихся

стратиграфически

[240].

Весь

комплекс вопросов, связанных с практической реализа-

цией

вероятностной схемы слоенакопления А. Н. Колмогорова,

подробно изложен в работе автора

[250].

Здесь лишь отметим,

что существо поставленной задачи по нахождению меры стабиль-

ности слоенакопления заключается в том, что необходимо сопо-

ставить

функции / (х) и /* (х) так, чтобы они в некотором смысле

(например, в смысле наименьших квадратов) наилучшим образом

определялись друг другом. / (х) — это нормированная на

единицу

функция, теоретически описывающая процесс слоенакопления,

которая находится в результате решения уравнения А. Н. Кол-

могорова

[146] при определенной плотности вероятности g (х).

(х) характеризуется гистограммой окончательных (зафиксиро-

ванных)

мощностей в разрезе. Поэтому задача сводится к про-

цедуре отыскания таких значений параметров функции / (х),

при которых построенная функция была бы сопоставима с гисто-

граммой

наблюдаемых в разрезе мощностей слоев.

Приведем схему решения задачи для двух наиболее характер-

ных плотпостей вероятностей распределения промежуточных мощ-

ностей слоев g (х).

Нормальная плотность g (х). Последовательные этапы нахо-

ждения вероятности сохранения слоя следующие.

1. Построение функции /* (х), т. е. гистограммы распределения

зафиксированных мощностей слоев.

Нахождение параметров а и G функции / (х) при ее сопо-

ставлении с функцией'/* (х). } (х) задается в виде

(х)

(х

—

а)'

exp

\ —

(х) ехр { - (Ь^Ц + F

(х) ехр { - > (174)

где а = а/о; х = xlc, х определяет положение абсциссы, при

которой вычисляется конкретное значение / (х), а

я/6

6ХР

( ~

T2iw)

(1?5)

где Ф (z) — интеграл вероятностей. Вся процедура по нахождению

и с с заранее заданной точностью алгоритмизирована. Программа

«Слой-1»,

составленная С. И. Романовским и А. М. Скворцовым,

осуществляет

перебор а и 0, которые задаются в заранее опре-

деленных диапазонах и перебираются с фиксированным шагом

до

получения

минимальной ошибки сопоставления

функций.

шагом 0,1 для а и а программа реализуется на ЭВМ БЭСМ-4

за

58 сек.

В зависимости от соотношения а ж о вычисление вероят-

ности сохранения в разрезе слоя

конечной

мощности по одной

из формул:

'0,52

+ 0,296 - при

0<-1,2;

° (176)

0,021+

th - при - > 1,2

l a

пли р =

—

(а/с),

когда а/о 1,5. (177)

Оценка точности расчетов р для случая, когда g (х) — нор-

мальная плотность, приведена в статье Ю. В. Адаменко и С. И. Ро-

мановского [б].

Полученные значения искомой вероятности далее интерпрети-

руются в содержательном плане в аспекте решаемой геологи-

ческой задачи. В частности, если реконструируется истинная

мощность гипотетических разрезов в отмеченном выше смысле,

то

с учетом меры, характеризующей стабильность слоенакопления,

истинная мощность анализируемого разреза восстанавливается

по формуле

Я*

-^У/1„

(178)

где H — мощность гипотетического разреза, или полная (суммар-

ная) амплитуда колебаний дна бассейна седиментации за интере-

сующий отрезок времени; Н* — наблюдаемая (анализируемая)

мощность слоев в фиксированной части разреза; р — вероятность

сохранения слоя; h

— мощность i-го слоя в выборочной совокуп-

ности мощностей слоев.

Ясно,

что при P = IH = #*, а с уменьшением р H превосхо-

дит //*, т. е. реально наблюдаемую суммарную мощность слоев.

Для

оценки

совокупной мощности размытых слоев можно

вос-

пользоваться

номограммой (рис. 57).

Отметим, что помимо уже упоминавшихся советских исследова-

телей модель слоенакопления А. Н. Колмогорова [146] для случая,

когда g (х) аппроксимируется законом

Гаусса,

использовали

японские геологи И. Хаттори и С. Мизутани [426, 493].