Рогов А.А, Семенова Е.Е, Чернецкий В.И, Щеголева Л.В - Уравнения математической физики. Сборник примеров и упражнений
Подождите немного. Документ загружается.

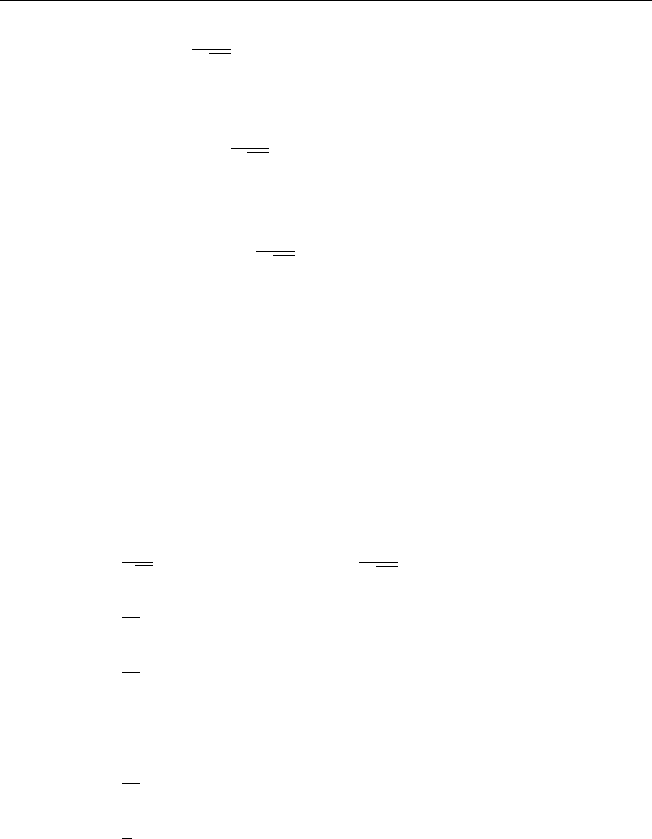
160 Глава V. Аналитические методы решения краевых задач
−a
2
λ
2
1
√
2π
Z
+∞
−∞
ue
−iλx
dx = −a
2
λ
2
U(λ, t).
Применив преобразование Фурье к начальным условиям (A2), получим
U( λ, 0) =
1
√
2π
Z
+∞
−∞
e
−iλx
f(x) dx = F (λ). (A3)
Таким образом, с помощью преобразования Фурье по переменной x :
U(λ, t) =
1
√
2π
Z
+∞
−∞
e
−iλx
u(x, t) dx, (A4)
исходную задачу (A1)-(A2) свели к задаче Коши с параметром λ :
U
t
+ a
2
λ
2
U = 0, t > 0, U(λ, 0) = F (λ), (A5)
решением которой является функция:
U(λ, t) = F (λ)e
−a
2
λ
2
t
.
Для построения решения исходной задачи к полученному выражению
для изображения U(λ, t) применим обратное преобразование Фурье.
Учитывая формулу (A3), будем иметь:
u(x, t) =
1
√
2π
Z
+∞
−∞
U(λ, t)e
iλx
dλ =
1
√
2π
Z
+∞
−∞
F (λ)e
−a
2
λ
2
t+iλx
dλ =
=
1
2π
Z
+∞
−∞
f(ξ)
Z
+∞
−∞
e
−a
2
λ
2
t
e
iλ(x−ξ)
dλ dξ =
=
1
2π
Z
+∞
−∞
f(ξ)
½
Z
+∞
0
e
−a
2
λ
2
t
e
iλ(x−ξ)
dλ +
+
Z
0
−∞
e
−a
2
λ
2
t
e
iλ(x−ξ)
dλ
¾
dξ =
=
1
2π
Z
+∞
−∞
f(ξ)
Z
+∞
0
e
−a
2
λ
2
t
(e
iλ(x−ξ)
+ e
−iλ(x−ξ)
) dλ dξ =
=
1
π
Z
+∞
−∞
f(ξ)
Z
+∞
0
e
−a
2
λ
2
t
cos λ(x −ξ) dλ dξ.
Вычислим интеграл
I(x) =
Z
+∞
0
e
−αλ
2
cos λx dλ, α > 0, (A6)
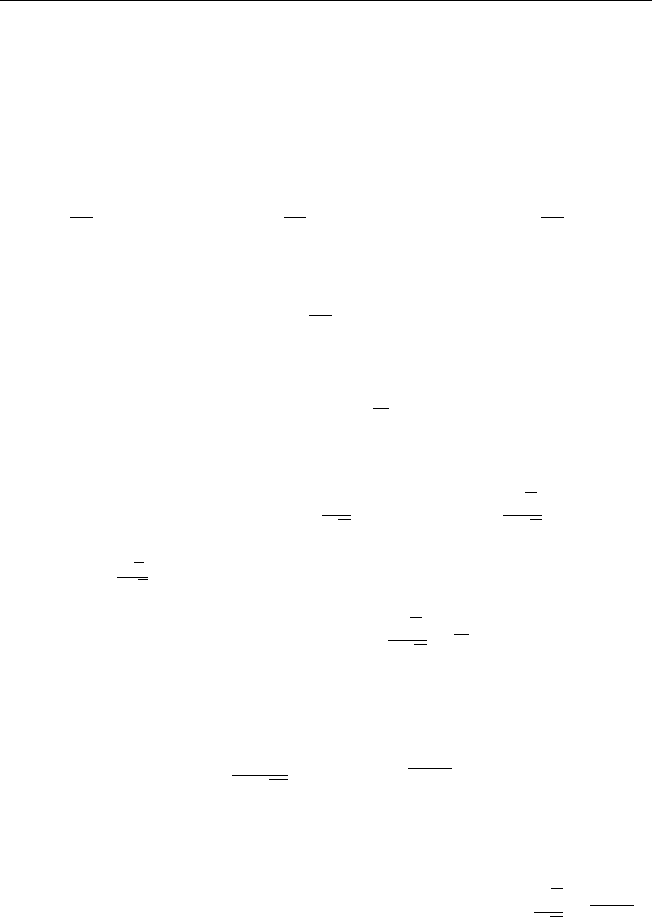
§ 5. Метод интегральных преобразований 161
который сходится при любых значениях параметра x (по признаку Вей-
ерштрасса). Дифференцируя интеграл (A6) по параметру x и применяя
правило интегрирования по частям:
I
0
(x) = −
Z
+∞
0
e
−αλ
2
λ sin λx dλ =
=
1
2α
e
−αλ
2
sin λx
¯
¯
¯
¯
λ=+∞
λ=0
−
x
2α
Z
+∞
0
e
−αλ
2
cos λx dλ = −
x
2α
I(x),
получим дифференциальное уравнение относительно I(x) :
I
0
(x) +
x
2α
I(x) = 0.
Его общее решение имеет вид
I(x) = C · e
−
x
2
α
.
Учитывая равенство
I(0) =
Z
+∞
0
e
−αλ
2
dλ =
1
√
α
Z
+∞
0
e
−γ
2
dγ =
√
π
2
√
α
,
найдем C =
√
π
2
√
α
и, следовательно, искомое значение интеграла (A6):
Z
+∞
0
e
−αλ
2
cos λx dλ =
√
π
2
√
α
e
−
x
2
α
.
Таким образом, окончательно выражение для решения краевой задачи
примет вид:
u(x, t) =
1
2a
√
πt
Z
+∞
−∞
f(ξ)e
−
(x−ξ)
2
4a
2
t
dξ. /
Замечание. В ходе решения задачи была установлена справедливость
следующих равенств:
Z
+∞
−∞
e
−a
2
λ
2
t+iλ(x−ξ )
dλ = 2
Z
+∞
0
e
−a
2
λ
2
t
cos λ(x −ξ) dλ =
√
π
√
α
e
−
(x−ξ)
2
α
.
(A7)
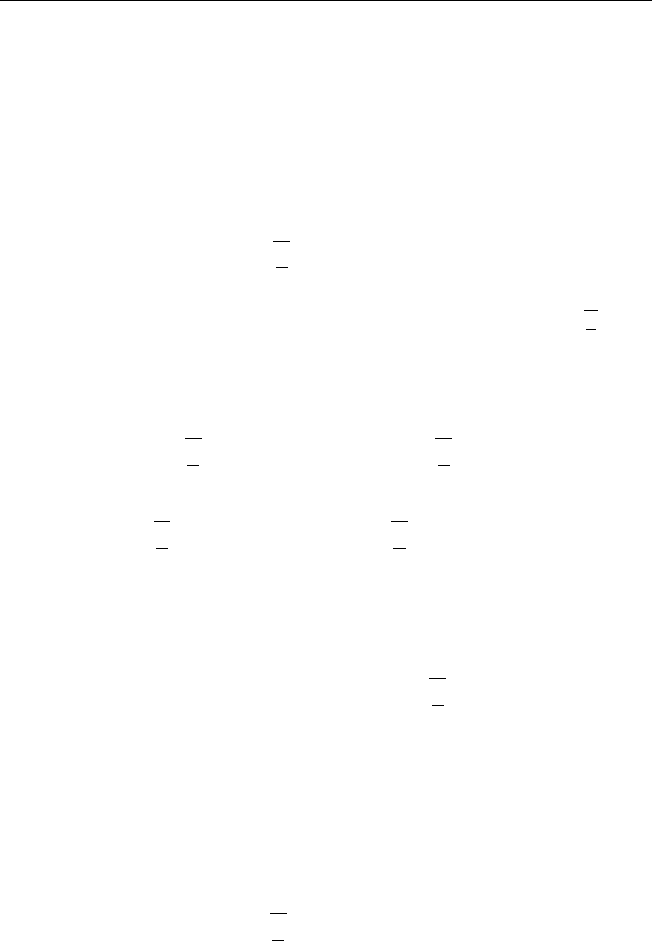
162 Глава V. Аналитические методы решения краевых задач
Пример 2. В первой четверти плоскости (x, t) найти решение краевой
задачи:
u
tt
= a
2
u
xx
, x, t > 0, (A1)
u(0, t) = µ(t), t > 0, (A2)
u(x, 0) = u
t
(x, 0) = 0, x > 0. (A3)
Решение.. Для решения задачи воспользуемся синус-преобразованием
Фурье по переменной x :
U( λ, t) =
r
2
π
Z
+∞
0
u(x, t) sin λx dx. (A4)
Умножим обе части уравнения (A1) на ядро преобразования
q
2
π
sin λx
и проинтегрируем полученное равенство по x на промежутке от 0 до
+∞. Преобразование левой части дает U
tt
(λ, t). К интегралу в правой
части применим правило интегрирования по частям, будем иметь:
U
tt
(λ, t) = a
2
r
2
π
Z
+∞
0
u
xx
sin λx dx = a
2
r
2
π
u
x
sin λx
¯
¯
¯
¯
¯
x=+∞
x=0
−
− a
2
r
2
π
λu cos λx
¯
¯
¯
¯
¯
x=+∞
x=0
− a
2
λ
2
r
2
π
Z
+∞
0
u sin λx dx.
Предполагая, что функция u(x, t) и ее производная u
x
стремятся к 0
при x → +∞, и используя граничные условия (A2), получим уравнение
относительно изображения U(λ, t) :
U
tt
(λ, t) = −a
2
λ
2
U(λ, t) + a
2
r
2
π
λµ(t). (A5)
Условия (A3) после применения к ним синус-преобразования Фурье да-
ют:
U(λ, 0) = U
t
(λ, 0) = 0. (A6)
Таким образом, исходная задача (A1)-(A3) редуцируется к задаче Коши
(A5)-(A6), в которой λ играет роль параметра. Решение уравнения (A5),
удовлетворяющее начальным условиям (A6), имеет вид
U(λ, t) = a
r
2
π
Z
t
0
µ(τ) sin aλ(t − τ ) dτ.

§ 5. Метод интегральных преобразований 163
С помощью обратного синус-преобразования Фурье будем иметь:
u(x, t) =
q
2
π
Z
+∞
0
U( λ, t) sin λx dλ
=
2a
π
Z
+∞
0
dλ
Z
t
0
µ(τ) sin λx · sin aλ(t − τ) dτ
=
2a
π
Z
t
0
µ(τ)
Z
+∞
0
sin λx ·sin aλ(t − τ ) dλ dτ.
Вычислим сначала внутренний интеграл. Так как
2
Z
+∞
0
sin λx ·sin aλ(t − τ ) dλ =
=
Z
+∞
0
cos λ[x −a(t −τ)] dλ −
Z
+∞
0
cos λ[x + a(t −τ)] dλ,
то, учитывая интегральное представление (в виде интеграла Фурье)
δ− функции Дирака
δ(x − x
0
) =
1
π
Z
+∞
0
cos λ(x −x
0
) dλ,
будем иметь
2
Z
+∞
0
sin λx ·sin aλ(t − τ ) dλ = π[δ(x − a(t − τ)) −δ(x + a(t − τ ))]
и, следовательно,
u(x, t) = a
Z
t
0
µ(τ)[δ(x − a(t − τ )) − δ(x + a(t − τ))] dτ =
=
Z
at
0
µ(t −
ξ
a
)[δ(x − ξ) − δ(x + ξ) dξ.
Так как δ(x + ξ) ≡ 0 при x > 0, то окончательно получаем
u(x, t) =
Z
at
0
µ(t −
ξ
a
)δ(x − ξ) dξ =
(
0 при t <
x
a
,
µ(t −
x
a
) при t >
x
a
. /

164 Глава V. Аналитические методы решения краевых задач
Пример 3. Найти решение краевой задачи:
u
t
= a
2
(u
xx
+ u
yy
), |x| < ∞, |y| < ∞, t > 0, (A1)
u(x, y , 0) = f(x, y), |x| < ∞, |y| < ∞. (A2)
Решение.. Применим кратное преобразование Фурье к функции
u(x, y, t) по двум пространственным переменным x и y, введя обозначе-
ние для изображения:
U(λ, µ, t) =
1
2π
Z
+∞
−∞
Z
+∞
−∞
u(ξ, η, t)e
−i(λξ+µη)
dξ dη.
Умножая уравнение (A1) и условие (A2) на ядро преобразования
e
−i(λx+µy)
и интегрируя полученное равенство по переменным x и y от
−∞ до +∞, применив правило интегрирования по частям и учитывая,
что функция u и ее производные u
x
и u
y
достаточно быстро стремятся
к нулю при x → ±∞, получим обыкновенное дифференциальное урав-
нение для изображения U :
U
t
+ a
2
(λ
2
+ µ
2
)U = 0, t > 0, (A3)
с начальным условием
U|
t=0
= F (λ, µ), (A4)
где
F (λ, µ) =
1
2π
Z
+∞
−∞
Z
+∞
−∞
f(ξ, η)e
−i(λξ+µη)
dξ dη. (A5)
Решением задачи (A3)-(A4) будет функция
U(λ, µ, t) = F (λ, µ)e
−a
2
(λ
2
+µ
2
)t
.
Решение исходной краевой задачи построим, выполнив обратное преоб-
разование Фурье:
u(x, y, t) =
1
2π
+∞
Z
−∞
+∞
Z
−∞
U( λ, µ, t)e
i(λx+µy)
dλ dµ =
=
1
2π
+∞
Z
−∞
+∞
Z
−∞
F (λ, µ)e
−a
2
(λ
2
+ν
2
)t
e
i(λx+µy)
dλ dµ =
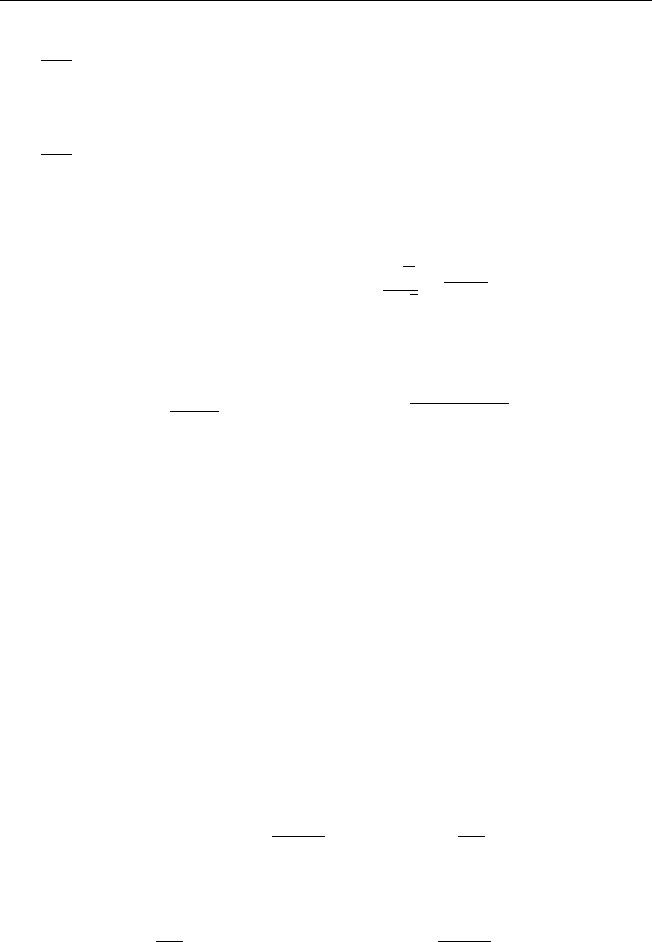
§ 5. Метод интегральных преобразований 165
=
1
4π
2
+∞
Z
−∞
+∞
Z
−∞
e
−a
2
(λ
2
+µ
2
)t
dλ dµ
+∞
Z
−∞
+∞
Z
−∞
f(ξ, η)e
iλ(x−ξ)+iµ( y−η)
dξ dη =
=
1
4π
2
+∞
Z
−∞
+∞
Z
−∞
f(ξ, η) dξ dη
+∞
Z
−∞
e
−a
2
λ
2
t
e
iλ(x−ξ)
dλ
+∞
Z
−∞
e
−a
2
µ
2
t
e
iµ(y−η)
dµ.
Так как (см. замечание к примеру 2)
+∞
Z
−∞
e
−a
2
λ
2
t
e
−iλ(x−ξ)
dλ =
√
π
a
√
t
e
−
(x−ξ)
2
4a
2
t
,
то окончательное выражение для искомого решения примет вид
u(x, y, t) =
1
4a
2
πt
Z
+∞
−∞
Z
+∞
−∞
f(ξ, η)e
−
(x−ξ)
2
+(y−η)
2
4a
2
t
dξ dη. /
Пример 4. С помощью преобразования Лапласа в области {(x, t) :
x > 0, t > 0} найти решение уравнения
u
t
= u
xx
+ u + B · cos x, (A1)
удовлетворяющее краевым условиям:
u(0, t) = A · e
−3t
, u
x
(0, t) = 0, (A2)
где A, B — постоянные величины.
Решение.. Применим преобразование Лапласа по переменной x:
u(x, t)
↔
U( p, t),
u
xx
↔
p
2
U(p, t) − p · u(0, t) − u
x
(0, t) = p
2
U(p, t) − p · A · e
−3t
,
B · cos x
↔
Bp
p
2
+ 1
, u
t
(x, t)
↔
∂U
∂t
.
После перехода к изображению относительно x уравнение (A1) примет
вид:
∂U
∂t
= (p
2
+ 1)U − p · A · e
−3t
+
Bp
p
2
+ 1
. (A3)

166 Глава V. Аналитические методы решения краевых задач
Полученное уравнение можно рассматривать как обыкновенное диффе-
ренциальное уравнение относительно t, в котором p играет роль пара-
метра. Общее решение уравнения (A3) можно представить в виде суммы
общего решения соответствующего однородного уравнения и частного
решения неоднородного уравнения:
U( p, t) = U
одн
(p, t) + U
частн
(p, t). (A4)
Общее решение соответствующего (A3) однородного уравнения имеет
вид:
U
одн
(p, t) = C
1
(p) · e
(p
2
+1)t
. (A5)
Частное решение ищем в виде:
U
частн
(p, t) = D
1
(p) · e
−3t
+ D
2
(p),
подставляя которое в уравнение (A3), получаем:
−3D
1
(p) · e
−3t
= (p
2
+ 1)(D
1
(p) · e
−3t
+ D
2
(p)) − p · A · e
−3t
+
Bp
p
2
+ 1
.
Отсюда для нахождения коэффициентов
D
1
(
p
)
и
D
2
(
p
)
,
зависящих от
параметра p, составляем систему уравнений:
(
−3D
1
(p) = D
1
(p)(p
2
+ 1) − pA,
(p
2
+ 1)D
2
(p) +
Bp
p
2
+1
= 0,
решение которой имеет вид:
D
1
(p) =
pA
p
2
+ 4
, D
2
(p) = −
Bp
(p
2
+ 1)
2
.
Таким образом, общее решение уравнения (A1) имеет вид:
U(p, t) = C
1
(p)e
(p
2
+1)t
+
pA
p
2
+ 4
e
−3t
−
Bp
(p
2
+ 1)
2
.
Используя свойство изображения U (p, t) → 0 при p → ∞, заключаем
C
1
(p) = 0. Следовательно, имеем:
U(p, t) =
pA
p
2
+ 4
e
−3t
−
Bp
(p
2
+ 1)
2
.

§ 5. Метод интегральных преобразований 167
Так как
p
p
2
+ 4
↔
cos 2x,
p
(p
2
+ 1)
2
=
p
p
2
+ 1
·
1
p
2
+ 1
↔
x
Z
0
cos ξ sin(x − ξ)dξ =
x
2
sin x,
то, используя свойство линейности преобразования Лапласа, получим
оригинал u(x, t).
Ответ: u(x, t) = Ae
−3t
cos 2x + B
x
2
sin x. /
Пример 5. В области {(x, t) : x > 0, t > 0} найти решение уравнения
9u
xx
+ 4u
tt
= 36 · e
2x
· sin 3t, (A1)
удовлетворяющее следующим условиям:
u(0, t) = 0, u
x
(0, t) = sin 3t, (A2)
u(x, 0) = 0, u
t
(x, 0) = 3x · e
2x
. (A3)
Решение.. Пусть U (p, t) – изображение по Лапласу функции
u(x, t):
U( p, t) =
∞
Z
0
e
−px
u(x, t)dx.
Тогда
u
xx
(x, t)
↔
p
2
U(p, t) − sin 3t, u
tt
↔
∂
2
U
∂t
2
.
Так как e
2x
↔
1
p−2
, то, применив к уравнению (A1) преобразование Ла-
пласа, получим:
9(p
2
U( p, t) − sin 3t) + 4
∂
2
U
∂t
2
=
36 · sin 3t
p − 2
. (A4)
Добавим к уравнению (A4) краевые условия
U(p, 0) = 0, U
t
(p, 0) =
3
(p − 2)
2
, (A5)
которые получены в результате применения преобразования Лапласа к
условиям (A3).
168 Глава V. Аналитические методы решения краевых задач
Решим задачу (A4)–(A5) с помощью преобразования Лапласа. Обозна-
чим через G(p, q) изображение по Лапласу относительно переменной t:
U(p, t)
↔
G(p, q ) =
∞
Z
0
e
−q t
U( p, t) dt. (A6)
Применив преобразование Лапласа к (A4), получим:
9p
2
G(p, q) −
27
q
2
+ 9
+ 4
µ
q
2
G(p, q) −
3
(p − 2)
2
¶
=
36 · 3
(p − 2)(q
2
+ 9)
. (A7)
Решим уравнение (A7) относительно функции G(p, q) :
G(p, q) =
3
(p − 2)
2
(q
2
+ 9)
.
Выполняя последовательно обратные преобразования Лапласа, будем
иметь:
U(p, t) =
1
(p − 2)
2
· sin 3t
↔
xe
2x
sin 3t.
Ответ: u(x, t) = x · e
2x
· sin 3t. /
Пример 6. Найти решение уравнения:
2u
xx
+ 5u
xt
+ 3u
tt
= 0, 0 < x, t < ∞, (A1)
удовлетворяющее условиям:
u(0, t) = 0, u
x
(0, t) = f (t); (A2)
u(x, 0) = g(x), u
t
(x, 0) = 0. (A3)
Решение.. Применим к решению уравнения преобразование Лапласа.
Обозначим через U(p, t) — изображение функции u(x, t) по переменной
x, G(p) — изображение функции g(x). Так как
u
xx
↔
p
2
U(p, t) − f (t),
u
tt
↔
U
tt
,
u
xt
↔
∂
∂t
(pU( p, t)) = pU
t
,
u(x, 0) = g(x)
↔
G(p),
u
t
(x, 0) = 0
↔
0,

§ 5. Метод интегральных преобразований 169
то после перехода к изображеням уравнение (A1) примет вид:
2p
2
U − 2f (t) + 5pU
t
+ 3U
tt
= 0. (A4)
Условия (A3) относительно изображений примут вид:
U( p, 0) = G(p), U
t
(p, 0) = 0. (A5)
К задаче (A4)—(A5) применим преобразование Лапласа по переменной
t. Пусть V (p, q) — изображение функции U (p, t), F (q) — изображение
функции f(t). Так как
U
t
↔
qV − G(p), U
tt
↔
q
2
V − qG(p),
то, применив преобразование Лапласа к уравнению (A4), получим:
(2p
2
+ 5pq + 3q
2
)V (p, q) = 2F (q) + 5pG(p) + 3qG(p). (A6)
Отсюда получаем
V (p, q ) =
2F (q) + 5pG(p) + 3qG(p)
2p
2
+ 5pq + 3q
2
. (A7)
Так как
(2p
2
+ 5pq + 3q
2
) = (p + q)(2p + 3q)
и
2F (q) + 5pG(p) + 3qG(p) = 2F (q) + 3pG(p) + (2p + 3q)G(p),
то выражение (A7) можно преобразовать следующим образом:
V (p, q ) =
2F (q) + 3pG(p)
(p + q)(2p + 3q)
+
G(p)
p + q
. (A8)
Так как
1
(p + q)(2p + 3q)
= −
1
p(p + q)
+
3
p(3q + 2p)
=
=
1
q
µ
1
p + q
−
2
2p + 3q
¶
,
то выражение (A8) примет вид:
V (p, q) =
2F (q)
q
µ
1
p + q
−
2
3q + 2p
¶
−
3G(p)
p + q
+
9G(p)
3q + 2p
+
G(p)
p + q
=
