Рогов А.А, Семенова Е.Е, Чернецкий В.И, Щеголева Л.В - Уравнения математической физики. Сборник примеров и упражнений

Подождите немного. Документ загружается.

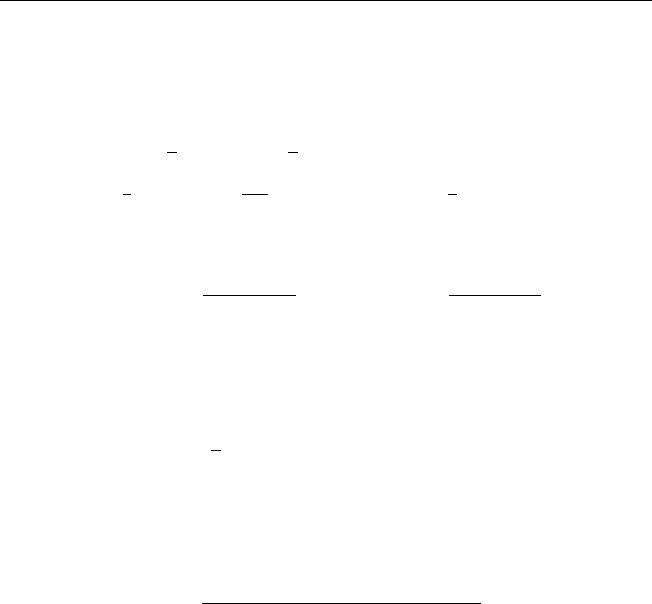
130 Глава V. Аналитические методы решения краевых задач

грал:

(x) dx =

(λ

cos λ

x + h sin λ

dx =

(λ

+ h

) +

(λ

− h

) cos 2λ

x + λ

h sin 2λ

dx =

(λ

+ h

) +

4λ

(λ

− h

) sin 2λ

l −

(cos 2λ

l − 1).

(A7)

Так как

sin 2λ

l =

2 tg λ

1 + tg

и cos 2λ

l =

1 − tg

1 + tg

и для λ = λ

справедливо равенство (A5) при любом k = 1, 2, . . . , то

путем несложных преобразований выражения (A7) получим следующее

выражение для квадрата нормы:

(h + l(λ

+ h

)), k = 1, 2, . . . /

• Можно получить общую формулу, выражающую собственные зна-

чения задачи Штурма-Лиувилля (3.4)-(3.6) через соответствующие им

собственные функции, в виде:

c =

(0)X(0) − X

(l)X(l) + kX

kXk

где связь между величинами X(0), X

(0), X(l) и X

(l) описывают усло-

вия (3.5), (3.6).

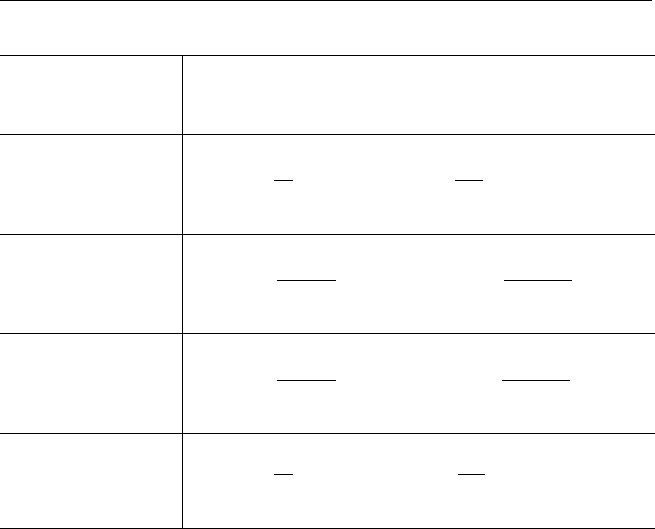
§ 3. Задача Штурма-Лиувилля 131

Простейшие задачи Штурма-Лиувилля для уравнения X

+ cX = 0

Вид условия Собственные значения и функции

X(0) = X(l) = 0 c

kπ

, X

(x) = sin

kπx

= l/2, k = 1, 2, . . .

(0) = X(l) = 0 c

(2k+1)π

, X

(x) = cos

(2k+1)πx

= l/2, k = 0, 1, 2, . . .

X(0) = X

(l) = 0 c

(2k+1)π

, X

(x) = sin

(2k+1)πx

= l/2, k = 0, 1, 2, . . .

(0) = X

(l) = 0 c

kπ

, X

(x) = cos

kπx

, k = 0, 1, 2, . . . ,

= l, kX

= l/2, k = 1, 2, . . .

Упражнения

23. Для уравнения (3.4) решите задачу Штурма-Лиувилля при следую-

щих условиях:

а) X(0) = X(l) = 0;

б) X

(0) = X(l) = 0;

в) X(0) = X

(l) = 0;

г) X

(0) = X

(l) = 0;

д) X(0) = X

(l) + h · X(l) = 0, h > 0;

е) X

(0) − h · X(0) = X

(l) = 0, h > 0;

ж) X

(0) − h · X(0) = X

(l) + h · X(l) = 0, h > 0.

24. Доказать, что собственные функции X

(x) и X

(x) задачи (3.4)-

(3.6), соответствующие различным собственным числам c

и c

132 Глава V. Аналитические методы решения краевых задач

(k 6= m), ортогональны, т.е.

, X

) =

(x) · X

(x) dx = 0.

25. Разложите по системе функций {sin

kπx

}, k = 1, 2, . . . , следующие

функции:

а) f(x) = 1; в) f(x) = x ·(l − x);

б) f(x) = x; г) f(x) = sin

8πx

26. Разложите по системе функций {cos

kπx

}, k = 0, 1, 2, . . . , функцию:

f(x) = x · (x − 1) + cos

x + 2 + 5 · cos

7πx

§4. Метод разделения переменных (Метод Фурье)

Обозначим через P

– дифференциальный оператор порядка m вида

≡

i=0

(t)

, (4.1)

где a

(t), i = 0, m, – заданные непрерывные функции (a

∈ C(R

)).

Для случая, когда m ≥ 1, рассмотрим смешанную задачу: найти реше-

ние u(x, t) уравнения

ρ(x)P

[u] =

∂

∂x

p(x)

∂u

∂x

− q(x)u, 0 < x < l, t > 0, (4.2)

удовлетворяющее однородным граничным условиям

∂u

∂x

+ β

u(x, t)

x=0

= 0,

∂u

∂x

+ β

u(x, t)

x=l

= 0

(4.3)

и начальным условиям

∂

u(x, 0)

∂t

= ϕ

(x), i = 0, m −1. (4.4)

§ 4. Метод разделения переменных 133

Будем считать, что функции ρ(x), p(x), q(x), входящие в уравнение

(4.2), заданы на промежутке (0, l) и обладают следующими свойствами:

1) ρ(x) > 0, p(x) > 0 для ∀x ∈ (0, l);

2) функции ρ(x), q(x) непрерывны на промежутке (0, l) (ρ, q ∈ C(0, l));

3) функция p(x) непрерывно дифференцируема на промежутке

(0, l) (p ∈ C

(0, l)).

При указанных ограничениях, накладываемых на функции ρ, p, q, и

m = 2 однозначно устанавливается тип уравнения (4.2) в зависимости

от знака функции a

(t) при ∀t > 0 :

если a

(t) > 0, то уравнение имеет гиперболический тип;

если a

(t) = 0, то уравнение имеет параболический тип;

если a

(t) < 0, то уравнение имеет эллиптический тип.

Решение задачи (4.2)-(4.4) может быть построено с помощью метода

разделения переменных (метода Фурье). Кратко изложим схему мето-

да.

Ненулевое решение будем искать в виде произведения двух функций

X(x) и T (t) :

u(x, t) = X(x)T (t). (∗)

Подставляя выражение (∗) в уравнение (4.2) и разделяя переменные,

получим:

p(x)

dX(x)

− q(x)

ρ(x)X(x)

[T (t)]

T (t)

. (∗∗)

Так как правая часть не зависит от x, а левая часть не зависит от t, то

для любых x и t равенство возможно, если оба отношения равны кон-

станте, скажем, −c. Тогда равенство (∗∗) распадается на два уравнения

p(x)

− q(x)X + cρ(x)X = 0, (4.5)

[T (t)] + cT (t) = 0, (4.6)

где c – пока неизвестная константа.

Подставляя выражение (∗) в граничные условия (4.3) и учитывая, что

T (t) 6≡ 0, получаем однородные условия для функции X(x) :

(0) + β

X(0) = 0, α

(l) + β

X(l) = 0. (4.7)

Таким образом, для смешанной задачи построена соответствующая за-

дача Штурма-Лиувилля (4.5), (4.7), решая которую получаем набор соб-

ственных значений c

и собственных функций X

(x).

134 Глава V. Аналитические методы решения краевых задач

Далее для каждого значения c

находится общее решение уравнения

(4.6) – функция T

(t) :

(t) =

j=1

(t), (4.8)

где {

(t)}

j=1

– фундаментальная система решений уравнения (4.6)

(при c = c

). И затем строится общее решение уравнения (4.2), удо-

влетворяющее граничным условиям (4.3), в виде ряда по собственным

функциям:

u(x, t) =

(t)X

(x) =

j=1

(t)X

(x). (4.9)

Входящие в него произвольные постоянные A

определяются подста-

новкой общего решения в начальные условия (4.4) (подчинением на-

чальным условиям):

∂

∂t

t=0

= u(x, 0) =

(i)

(0)X

(x) = ϕ

(x), i = 0, m − 1.

При этом заданные функции ϕ

(t) требуется разложить в ряд по системе

собственных функций

(x) =

(x).

Откуда получаем уравнения для определения величин A

(i)

(0) =

j=1

(i)

(0) = α

, i = 0, m − 1.

При соблюдении условий, налагаемых на функции ϕ

, обеспечивающих

равномерную сходимость ряда

(t)X

(x)

и рядов, полученных из него почленным дифференцированием доста-

точное число раз, получаем классическое решение задачи (4.2)-(4.4).

Пример 1. В полуполосе D = {(x, y) : 0 < x < l, t > 0} найти реше-

ние уравнения U

= a

, удовлетворяющее однородным граничным

§ 4. Метод разделения переменных 135

условиям:

U(0 , t) = U(l, t) = 0

и начальным условиям:

U(x, 0) = 0, U

(x, 0) = sin

2π

Решение.. Будем искать решение в виде U (x, t) = T (t)X(x). Так как

= T

(t)X(x) и U

= T (t)X

(x),

то, подставив выражения для производных U

, U

в заданное уравне-

ние и разделив переменные, получим

(t)

T (t)

(x)

X(x)

Равенство должно выполняться при любых x и t из рассматриваемой

области, что возможно, если оба отношения равны некоторой константе,

то есть

(t)

T (t)

(x)

X(x)

= −c, c = const, (A1)

откуда получаем два дифференциальных уравнения с параметром c :

+ cX = 0 и T

+ ca

T = 0.

Первое уравнение, учитывая однородные граничные условия U(0, t) =

U(l, t) = 0, дает для функции X(x) задачу Штурма-Лиувилля:

(x) + cX(x) = 0, 0 < x < l,

X(0) = X(l) = 0,

решением которой будут собственные числа c

= (

kπ

)

и соответствую-

щие им собственные функции X

(x) = sin

kπ

x, k = 1, 2, . . .

Остается для каждого значения c = c

найти решение второго уравне-

ния для функции T (t) :

(t) + a

T (t) = 0,

общее решение которого при различных k имеет вид:

(t) = A

cos

aπk

t + B

sin

aπk

136 Глава V. Аналитические методы решения краевых задач

Тогда, согласно методу Фурье, решение заданного уравнения запишем

в виде ряда:

U(x, t) =

∞

k=1

cos

aπk

t + B

sin

aπk

· sin

kπ

x, (A3)

предполагая, что он допускает двукратное почленное дифференцирова-

ние. Чтобы найти неизвестные константы A

, B

, подчиним функцию

U(x, t) в виде (A3) начальным условиям:

U(x, 0) =

∞

k=1

sin

kπ

x = 0,

(x, 0) =

∞

k=1

aπk

sin

kπ

x = sin

2π

Из первого соотношения следует, что A

= 0, ∀k = 1, 2, . . . Для то-

го чтобы найти коэффициенты B

, необходимо разложить функцию

в правой части второго равенства в ряд по собственным функциям

sin

kπ

∞

k=1

и приравнять коэффициенты при одинаковых собствен-

ных функциях в разложениях справа и слева. Но так как функция

sin

2π

x сама является собственной, то имеем:

= 0 для k 6= 2, B

2aπ

= 1.

Cледовательно, так как среди коэффициентов A

и B

только один

ненулевой: B

2aπ

, то искомое решение будет содержать только одно

слагаемое ряда (A3) при k = 2.

Ответ: U (x, t) =

2aπ

sin

2aπ

t · sin

2π

x. /

Пример 2. В полуполосе D = {( x, y) : 0 < x < l, t > 0} найти решение

смешанной задачи:

= a

− βu, (A1)

(0, t) −hu(0, t) = u

(l, t) = 0, h > 0, (A2)

u(x, 0) = u

, (A3)

β, h, u

− const.

Решение.. Применяя метод разделения переменных, будем искать

ненулевое решение в виде

u(x, t) = X(x) · T (t), X(x) 6≡ 0, T (t) 6≡ 0. (A4)

§ 4. Метод разделения переменных 137

Подставим выражение (A4) в уравнение (A1):

X · T

= a

· T − βX · T.

Разделив переменные, получим равенство двух отношений, одно из ко-

торых зависит только от t, а другое – от x. Такое равенство возможно,

если отношения являются постоянными величинами:

+ βT

= −c = const.

Отсюда получаем два уравнения:

+ (β + a

c)T = 0, (A5)

+ cX = 0. (A6)

Потребуем, чтобы решение вида (A4) удовлетворяло граничным усло-

виям (A2):

(0, t) −hu(0, t) = (X

(0) − hX(0))T (t) = 0,

(l, t) = X

(l)T (t) = 0.

Так как условия должны выполняться для любых t ≥ 0 и T (t) 6≡ 0, то

будем иметь

(0) − hX(0) = 0 и X

(l) = 0.

Таким образом, для заданной смешанной задачи получили соответству-

ющую задачу Штурма-Лиувилля:

+ cX = 0, 0 < x < l,

(0) − hX(0) = X

(l) = 0.

(A7)

Из общей теории известно, что собственные значения задачи (A7) по-

ложительны, c > 0. Тогда общее решение уравнения задачи (A7) имеет

вид:

X(x) = A cos λx + B sin λx, (A8)

где λ =

√

c > 0. Подчиняя выражение (A8) заданным условиям задачи

(A7), получим

(

λB − hA = 0,

−Aλ sin λl + Bλ cos λl = 0

⇔

(

B =

A sin λl − B cos λl = 0.

(A9)

138 Глава V. Аналитические методы решения краевых задач

Полученная система будет иметь ненулевое решение, если определитель

матрицы системы равен нулю, т.е. если будет выполнено равенство

sin λl −

cos λl = 0 ⇔ tg λl =

. (A10)

Уравнение (A10) имеет счетное множество решений. Рассматривая

только положительные корни уравнения (A10) (объясните, почему?),

получим собственные числа задачи (A7):

= λ

, где tg λ

l =

, k = 1, 2, . . .

и соответствующие им собственные функции вида (A8):

(x) = A

(cos λ

x +

sin λ

x). (A8

)

Так как

= tg λ

l, то, полагая A

= cos λ

l, получим

(x) = cos λ

l cos λ

x + sin λ

l sin λ

x = cos λ

(x − l). (A11)

Для каждого k = 1, 2, . . . построим общее решение уравнения (A5):

(t) = D

−(β+a

Тогда частное решение уравнения (A1), удовлетворяющее граничным

условиям (A2), запишется в виде:

(x, t) = X

(x)T

(t) = D

−(β+a

cos λ

(x − l).

Используя принцип суперпозиции, построим решение уравнения (A1):

u(x, t) =

∞

k=1

(x, t) =

∞

k=1

−(β+a

cos λ

(x − l). (A12)

Осталось подчинить выражение (A12) начальному условию (A3):

u(x, 0) =

∞

k=1

cos λ

(x − l) =

∞

k=1

(x) = u

§ 4. Метод разделения переменных 139

Собственные функции X

(x) (A11) задачи Штурма-Лиувилля (A7) ор-

тогональны на отрезке [0; l] с весом ρ(x) ≡ 1, поэтому имеем:

(x) dx = D

(x) dx ⇒ D

(x) dx

, (A13)

k = 1, 2, . . .

– коэффициенты разложения функции f (x) = u

в ряд по системе

(x)}|

∞

k=1

. Вычислим интегралы, входящие в выражение для коэф-

фициента D

. Рассмотрим интеграл в числителе:

(x) dx =

cos λ

(x − l) dx =

sin λ

Интеграл в знаменателе выражения (A13) определяет квадрат нормы

собственной функции (A11):

(x) dx =

cos

(x − l) dx =

4λ

sin 2λ

Преобразуем последнее выражение, учитывая равенства:

sin 2λ

l =

2 tg λ

1 + tg

и tg λ

l =

получим

k X

(x) dx =

l(λ

+ h

) + h

2(λ

+ h

)

Таким образом, коэффициенты D

ряда (A12) равны

= u

2(λ

+ h

)

l(λ

+ h

) + h

sin λ

И, следовательно, решение задачи (A1)-(A3) имеет вид:

u(x, t) = 2u

∞

k=1

2(λ

+ h

) sin λ

[l(λ

+ h

) + h]

−(β+a

cos λ

(x − l), (A14)

где λ

– положительные корни уравнения tg λl =