Рогов А.А, Семенова Е.Е, Чернецкий В.И, Щеголева Л.В - Уравнения математической физики. Сборник примеров и упражнений

Подождите немного. Документ загружается.

140 Глава V. Аналитические методы решения краевых задач

Замечание. Если выбрать собственные функции X

(x) задачи (A7) сле-

дующим образом:

(x) = λ

cos λ

x + h sin λ

полагая в (A8

) A

= λ

, то можно построить решение задачи (A1)-(A3)

в виде:

u(x, t) = 2u

∞

k=1

[l(λ

+ h

) + h]

−(β+a

(λ

cos λ

x + h sin λ

x).

(A15)

Путем несложных преобразований выражение (A15) можно привести к

виду (A14) (выполните это самостоятельно). /

• Решение неоднородных задач также может быть найдено с помощью

метода Фурье. При этом решение неоднородного уравнения, удовлетво-

ряющего однородным граничным условиям, находится в виде ряда по

собственным функциям соответствующей задачи Штурма-Лиувилля.

Смешанную задачу с неоднородными граничными условиями предва-

рительно следует редуцировать (свести) к задаче с однородными гра-

ничными условиями.

Пример 3. В полуполосе D = {(x, t) : 0 < x < l, t > 0} найти решение

краевой задачи:

= U

+ 2b, b = const, (A1)

U(0, t) = U(l, t) = 0, U(x, 0) = U

(x, 0) = 0.

Решение.. Построив c помощью соответствующего заданному од-

нородного уравнения U

= U

и однородных граничных условий

U(0, t) = U(l, t) = 0 задачу Штурма-Лиувилля:

(x) + cX(x) = 0, 0 < x < l, X(0) = X(l) = 0,

найдем собственные функции и собственные числа краевой задачи:

(x) = sin

kπ

x, c

kπ

, k ∈ N.

Общее решение уравнения (A1) будем искать в виде ряда по собствен-

ным функциям задачи с переменными коэффициентами T

(t):

U(x, t) =

∞

k=1

(t)X

(x) =

∞

k=1

(t) sin

kπ

x. (A2)

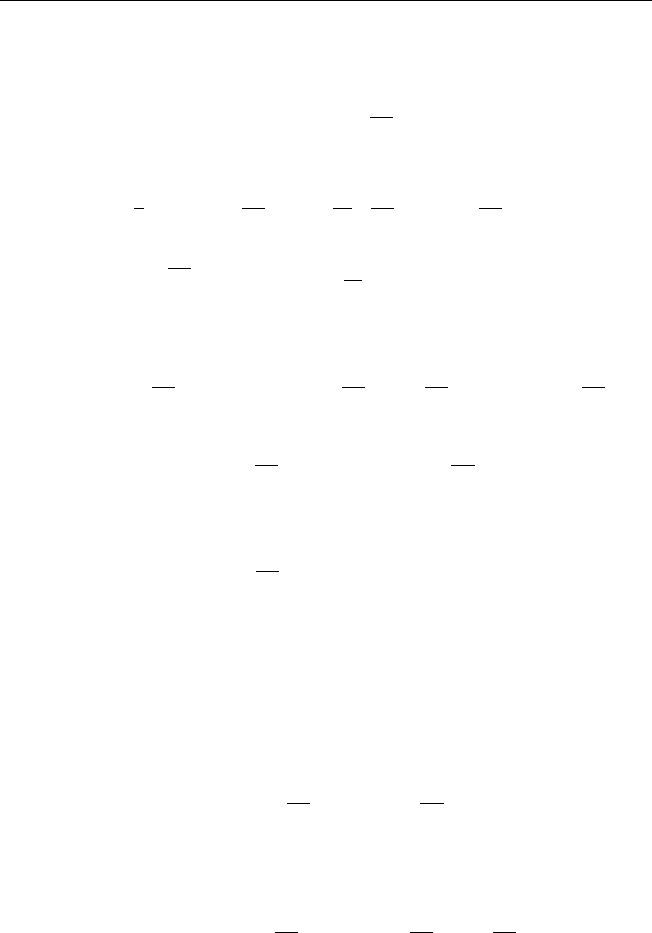
§ 4. Метод разделения переменных 141

Входящую в уравнение функцию f(x, t) = 2b разложим в ряд по соб-

ственным функциям X

(x) :

2b =

∞

k=1

sin

kπ

x, (A3)

где

2b · sin

kπ

x dx =

kπ

−cos

kπ

= −

kπ

[(−1)

− 1] =

0, k − четное

kπ

, k − нечетное.

Подставляя разложения (A2) и (A3) в заданное уравнение (A1), будем

иметь

∞

k=1

(t) · sin

kπ

x = −

∞

k=1

(t) ·

kπ

sin

kπ

x +

∞

k=1

· sin

kπ

∞

k=1

(t) +

kπ

(t) − f

· sin

kπ

x = 0.

Из последнего равенства получаем уравнения для функций T

(t) :

(t) +

kπ

(t) = f

, k ∈ N. (A4)

Подставляя разложение (A2) в заданные начальные условия U(x, 0) =

(x, 0) = 0, получим:

(0) = T

(0) = 0, ∀k ∈ N. (A5)

Таким образом, для каждого k ∈ N функция T

(t) является решением

задачи Коши для уравнения (A4) с условиями (A5), которое имеет вид

(t) = f

kπ

1 − cos

kπ

Подставляя найденные выражения для функций T

в ряд (A2) для

функции U( x, t), получим искомое решение

U(x, t) =

∞

k=1

kπ

· [1 − cos

kπ

t] · sin

kπ

142 Глава V. Аналитические методы решения краевых задач

которое с учетом значений коэффициентов f

можно записать в виде

U(x, t) =

∞

k=1

8bl

(2k − 1)

1 − cos

(2k −1)π

· sin

(2k −1)π

x. /

Пример 4. В полуполосе D = {(x, t) : 0 < x < π, t > 0} найти решение

краевой задачи:

= 4U

+ x(3e

+ 1), (A1)

U(0 , t) = 0, U

(π, t) = t + 2, (A2)

U(x, 0) = 2x + 3 sin

. (A3)

Решение.. Приведем исходную задачу (A1)-(A3) к задаче с однород-

ными граничными условиями. Для этого будем искать ее решение в

виде суммы двух функций

U(x, t) = V (x, t) + W (x, t), (A4)

подобрав функцию W (x, t) таким образом, чтобы она удовлетворяла

условиям:

W (0, t) = 0, W

(π, t) = t + 2, ∀t > 0. (A5)

Функцию, удовлетворяющую указанным условиям, можно искать в ви-

де линейной комбинации граничных условий:

W (x, t) = (γx + δ)(t + 2). (A6)

Неизвестные константы γ и δ найдем, подчинив выражение (A6) усло-

виям (A5):

(

W (0, t) = δ(t + 2) = 0,

(π, t) = γ(t + 2) = t + 2.

Откуда заключаем, что δ = 0 и γ = 1, и, следовательно, функцию

W (x, t), удовлетворяющую условиям (A5), можно выбрать в виде:

W (x, t) = x(t + 2).

Теперь с учетом выбранной функции W (x, t) решение исходной задачи

будем искать в виде

U(x, t) = V (x, t) + x(t + 2). (A7)

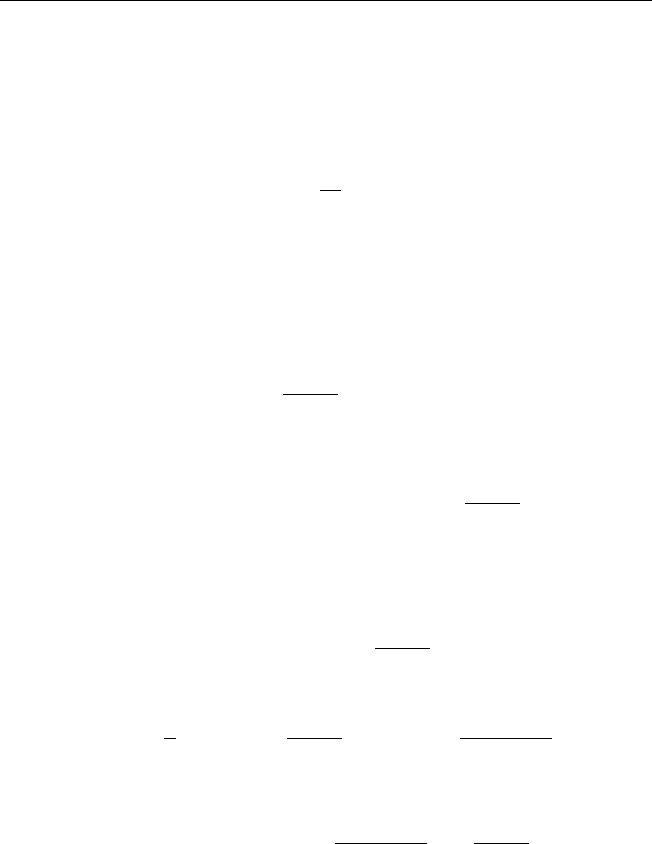
§ 4. Метод разделения переменных 143

Подставляя это выражение в уравнение (A1) и условия (A2), (A3), полу-

чим задачу относительно функции V (x, t) с однородными граничными

условиями:

= 4V

+ 3xe

, 0 < x < π, t > 0, (A8)

V (0, t) = 0, V

(π, t) = 0, t ≥ 0, (A9)

V (x, 0) = 3 sin

, 0 ≤ x ≤ π. (A10)

Решение краевой задачи (A8)-(A10) будем искать в виде ряда по соб-

ственным функциям соответствующей задачи Штурма-Лиувилля:

(x) + cX(x) = 0, 0 < x < π, X(0) = X

(π) = 0,

которая определяет следующий набор собственных функций:

(x) = sin

2k + 1

x, k = 0, 1, . . .

Тогда выражение для функции V (x, t) запишем в виде:

V (x, t) =

∞

k=0

(t)X

(x) =

∞

k=0

(t) sin

2k + 1

x. (A11)

Разложим в ряд по системе функций {X

(x)}|

∞

k=0

неоднородное слагае-

мое в уравнении (A8):

3xe

∞

k=0

(t) sin

2k + 1

x, (A12)

где

(t) =

3xe

sin

2k + 1

x dx = (−1)

24e

π(2k + 1)

Подстановка разложений (A11) и (A12) в уравнение (A8) дает

∞

k=0

+ (2k + 1)

− (−1)

24e

π(2k + 1)

sin

2k + 1

x = 0.

Откуда для нахождения функций T

(t) получаем уравнения

+ (2k + 1)

= γ

, k = 0, 1, . . . ,

144 Глава V. Аналитические методы решения краевых задач

где

= (−1)

π(2k + 1)

К ним добавим условия

(0) = 0 ∀k 6= 1, T

(0) = 3,

которые получаются приравниванием коэффициентов при одинаковых

собственных функциях после подстановки выражения (A11) для функ-

ции V (x, t) в начальное условие (A10). Для каждого k нетрудно постро-

ить решения соответствующих задач Коши:

(t) =

(2k + 1)

+ 1

− e

−(2k+1)

, ∀k 6= 1,

(t) =

− e

−9t

+ 3e

−9t

и, подставив найденные выражения для функций T

(t) в ряд (A11),

получить решение задачи (A8)-(A10):

V (x, t) =

∞

k=0

(−1)

− e

−(2k+1)

)

(2k + 1)

[(2k + 1)

+ 1]

sin

2k + 1

x + 3e

−9t

sin

(A13)

Следовательно, искомое решение имеет вид U (x, t) = x(t + 2) + V (x, t),

в котором функция V (x, t) определена выражением (A13).

• С помощью метода разделения переменных можно строить решения

смешанных задач и в том случае, когда количество независимых пере-

менных больше двух.

Пример 5. Однородная прямоугольная мембрана (0 ≤ x ≤ l, 0 ≤

y ≤ b), закрепленная вдоль всего контура, лежащего в горизонтальной

плоскости, имела в начальный момент форму u(x, y, 0) = ϕ(x, y) и нача-

ла колебаться с начальной скоростью u

(x, y, 0) = ψ(x, y). Найти закон

свободных колебаний мембраны, если натяжение мембраны T

равно ее

поверхностной плотности (т.е. a

= 1).

Решение.. Предполагая, что мембрана совершает малые колебания,

определение закона свободных колебаний мембраны сводится к реше-

нию первой краевой задачи: найти решение волнового уравнения

= u

+ u

, 0 < x < l, 0 < y < b, (A1)

§ 4. Метод разделения переменных 145

удовлетворяющее начальным условиям:

u(x, y , 0) = ϕ(x, y), u

(x, y , 0) = ψ(x, y) (A2)

и граничным условиям:

u(0, y , t) = u(l, y, t) = u(x, 0, t) = u(x, b, t) = 0. (A3)

Будем искать ненулевое решение уравнения (A1) в виде произведения:

u(x, y, t) = X(x)Y (y)T (t). (A4)

Подставив выражение (A4) в уравнение (A1), получим равенство

XY = (X

Y + XY

)T,

разделив которое на XY T, будем иметь

Каждое из входящих в последнее равенство отношений зависит от сво-

ей переменной, поэтому при любых x, y, t из рассматриваемой области

задания независимых переменных равенство возможно, если эти отно-

шения постоянны, т.е.

= −λ,

= −µ и

= −(λ + µ). (A5)

Используя граничные условия (A3), получим две задачи Штурма-Лиу-

вилля для функций X(x) и Y (y) :

+ λX = 0, X(0) = X(l) = 0, (A6)

+ µY = 0, Y (0) = Y (b) = 0, (A7)

которые имеют следующие решения соответственно:

kπ

, X

(x) = sin

kπx

, k = 1, 2, . . . ;

mπ

, Y

(y) = sin

mπy

, m = 1, 2, . . .

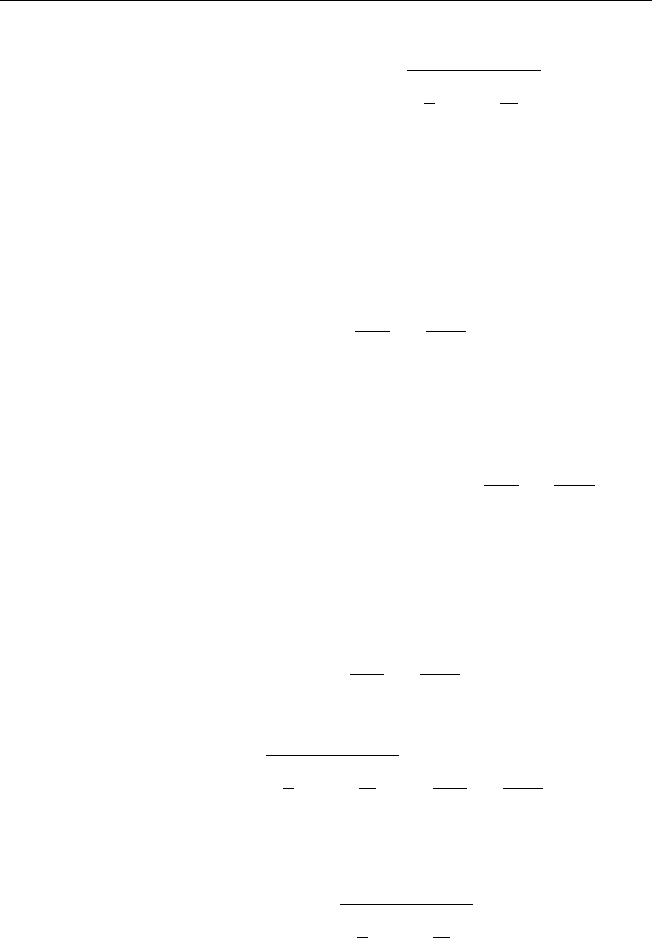
146 Глава V. Аналитические методы решения краевых задач

Тогда функция T ( t) должна удовлетворять уравнению:

(t) + γ

T (t) = 0, γ

= π

общее решение которого при различных k и m дают функции

(t) = A

cos γ

t + B

sin γ

Таким образом, функции

(x, y , t) = X

(x)Y

(y)T

(t) =

= (A

cos γ

t + B

sin γ

t) sin

kπx

sin

mπy

, k, m ∈ N (A8)

удовлетворяют уравнению (A1) и граничным условиям (A3). Из линей-

ности уравнения (A1) следует, что и любая комбинация решений (A8),

т.е. формально составленный двойной ряд:

u(x, y, t) =

∞

k=1

∞

m=1

cos γ

t + B

sin γ

t) sin

kπx

sin

mπy

(A9)

при условии, что он допускает двукратное почленное дифференцирова-

ние, также является решением уравнения (A1), удовлетворяющим усло-

виям (A3). Подчиним функцию u(x, y, t), представленную рядом (A9),

заданным начальным условиям:

u(x, y, 0) =

∞

k=1

∞

m=1

sin

kπx

sin

mπy

= ϕ(x, y)

(x, y , 0) =

∞

k=1

∞

m=1

sin

kπx

sin

mπy

= ψ(x, y).

Откуда можно сделать вывод, что ряд (A9) будет определять искомое

решение, если величины

и B

§ 4. Метод разделения переменных 147

являются коэффициентами Фурье функций ϕ(x, y) и ψ(x, y) соответ-

ственно, т.е.

ϕ(x, y) sin

kπx

sin

mπy

dy dx (A10)

(kb)

+ (ml)

ψ(x, y) sin

kπx

sin

mπy

dy dx. (A11)

Замечание. Ряд (A9), в котором коэффициенты A

и B

опреде-

ляются по формулам (A10), (A11), дает классическое решение кра-

евой задачи, если функции ϕ(x, y) и ψ(x, y) удовлетворяют гранич-

ным условиям и принадлежат классу функций C

в прямоугольнике:

0 ≤ x ≤ l, 0 ≤ y ≤ b. /

Пример 6. Найти стационарное распределение температуры в прямо-

угольнике D = {(x, y) : 0 ≤ x ≤ a, 0 ≤ y ≤ b}, если на границе области

D поддерживается заданная температура:

u(x, o) = u(x, b) = 0, 0 < x < a, (A1)

u(0, y) = ϕ(y) = y(b − y), u(a, y) = ψ(y) = sin

3πy

, 0 < y < b. (A2)

Решение.. Определение стационарного распределения температуры

сводится к решению краевой задачи для уравнения Лапласа:

∆u = u

+ u

y y

= 0 (A3)

с заданными граничными условиями. Будем искать решение уравнения

(A3) в виде произведения

u(x, y ) = X(x) · Y (y), (A4)

подставив которое в уравнение (A3) и разделив переменные, получим

два уравнения:

= −

= c = const. (A5)

Подстановка выражения (A4) в однородные граничные условия (A1)

дает условия для функции Y (y) :

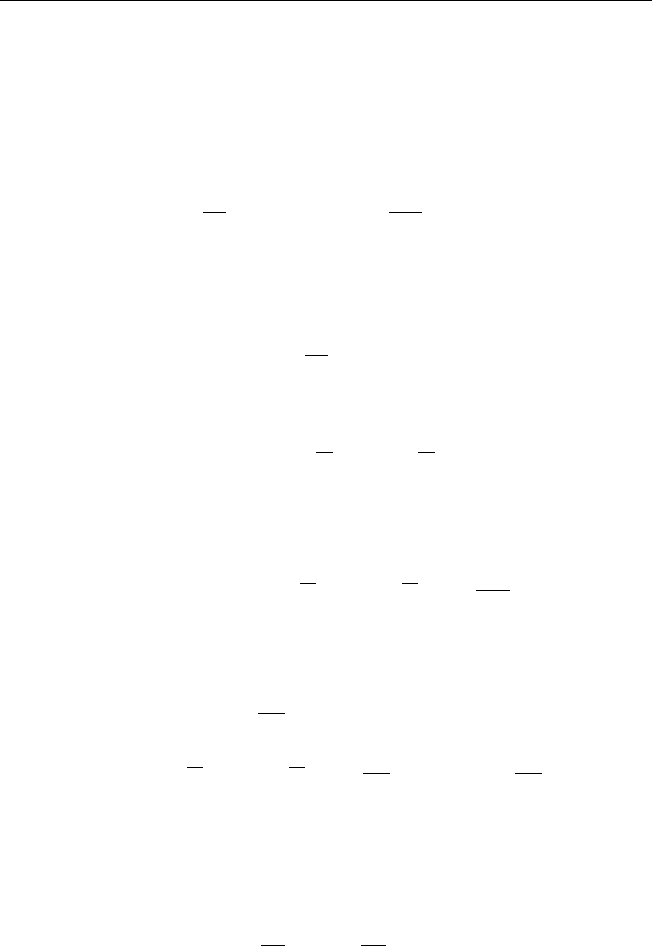
148 Глава V. Аналитические методы решения краевых задач

Y (0) = Y (b) = 0,

которые вместе с уравнением

+ cY = 0, 0 < y < b

приводят к задаче Штурма-Лиувилля. Ее решением будут собственные

числа и собственные функции:

kπ

, Y

(y) = sin

kπy

, k ∈ N. (∗)

Подставляя найденные значения c

во второе уравнение (A5), для функ-

ции X(x) получим уравнение

−

kπ

X = 0.

Для различных k ∈ N его решением будут функции

(x) = A

kπ

+ B

−

kπ

Тогда решение уравнения (A3), удовлетворяющее граничным условиям

(A1), запишем в виде:

u(x, y) =

∞

k=1

kπ

+ B

−

kπ

sin

kπy

. (A6)

Потребуем, чтобы функция u(x, y) в виде (A6) удовлетворяла гранич-

ным условиям (A2):

u(0, y) =

∞

k=1

+ B

) sin

kπy

= ϕ(y) = y(b − y);

u(a, y) =

∞

k=1

kπ

+ B

−

kπ

sin

kπy

= ψ(y) = sin

3π y

Рассматривая полученные равенства как разложения функций ϕ(y) и

ψ(y) в ряд по собственным функциям Y

(y), получим для каждого

k ∈ N систему уравнений:

(

= α

kπ a

+ B

−

kπa

= β

(A7)

§ 4. Метод разделения переменных 149

где

ϕ(y) sin

kπy

dy =

y(b − y) sin

kπy

dy =

(1 − (−1)

), k ∈ N;

= 0 ∀k 6= 3, β

= 1.











(A8)

Решая систему линейных уравнений (A7) относительно A

и B

, для

каждого k ∈ N найдем

− α

−

kπa

2 sh

kπa

, B

kπ a

− β

2 sh

kπa

. (A9)

Подставляя выражения для коэффициентов A

и B

(A9) в ряд (A6),

получим решение краевой задачи:

u(x, t) =

∞

k=1

kπx

− α

kπ(x − a)

sin

kπy

sin

kπa

или с учетом соотношений (A8)

u(x, y ) =

3πx

3πa

sin

3πy

−

∞

k=0

sin

kπy

(2k + 1)

kπ(x−a)

kπa

. /

Упражнения

I. Однородные уравнения с однородными граничными условиями

27. Дан тонкий однородный стержень длиной l, на концах которого под-

держивается нулевая температура. Начальное распределение темпе-

ратуры стержня описывается функцией f(x ). Найти распределение

температуры вдоль стержня при t > 0. Найти решение в случае,

когда

f(x) =

(

x, 0 < x ≤

l − x,

< x < l.