Roff D.A. Modeling Evolution: An Introduction to Numerical Methods

Подождите немного. Документ загружается.

N.resident <- N.invader <- matrix(0,Tot.Gen) # Allocate space

N.resident[1] <- 1 # Initial pop size of resident

N.invader[Maxgen1] <- 1 # Initial pop size of invader

for (Igen in 2:Maxgen1) # Iterate over generations with resident

only

{

N <- N.resident[Igen-1]

N.resident[Igen] <- DD.FUNCTION(ALPHA.resident, N, N)

} # End of 1st Igen loop

# Now add invader

J <- Maxgen1þ1 # Starting generation

for (Igen in J:Tot.Gen) # Iterate over generations with invader

{

N <- N.resident[Igen-1]þ N.invader[Igen-1] # Total pop size

N.resident[Igen] <- DD.FUNCTION(ALPHA.resident, N.resident

[Igen-1], N)

N.invader[Igen] <- DD.FUNCTION(ALPHA.invader, N.invader[Igen-

1], N)

} # End of 2nd Igen loop

Generation <- seq(from¼1, to¼Tot.Gen) # Vector of generation

numbers

plot (Generation, N.resident, xlab¼’Generation’, ylab¼’Resident

N’, type¼’l’)

plot (Generation, N.invader, xlab¼’Generation’, ylab¼’Invader

N’, type¼’l’)

} # End of function

############## MAIN PROGRAM ##############

par(mfrow¼c(2,2)) # Divide graphics page into quadrats

Best.A <- 24.21635 # Best alpha from elasticity analysis

Invader.A <- 10 # Alpha for invader

Coeff <- Invader.A/Best.A # Calculate relevant coefficient

POP.DYNAMICS( Best.A,Coeff) # Call functiom

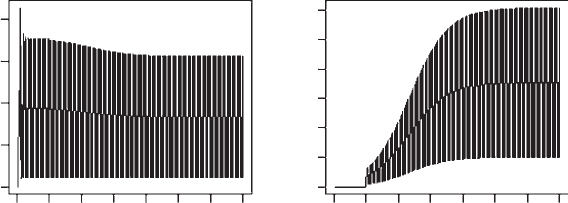
OUTPUT: (Figure 3.18)

Generation

Resident N

Invader N

0 102030405060

200 400 600 800

50 100 200 300

Generation

0 50 100 200 300

Figure 3.18 Temporal plots of resident and invader populations. Left‐hand plot shows the

population trajectory for the optimum a and the right‐hand plot shows the population

trajectory for an invader with a = 10.

218 MODELING EVOLUTION

It is evident from the output that an invader with  ¼ 10 can invade the popula-

tion but not replace the resident population. This explains the relation between

the invasion coefﬁcient and the optimum  and emphasizes the importance of

elasticity analysis in conjunction with pairwise invasibility analysis.

3.8.5 Multiple invasibility analysis

The program is the same as in Scenario 6 except for: (a) it is run 10,000 generations

to ensure sufﬁcient time for equilibrium to be attained (if possible), ( b) because the

elasticity analysis indicated that a single equilibrium is unlikely, frequency poly-

gons are plotted for the last three generations.

R CODE:

rm(list¼ls()) # Clear memory

DD.FUNCTION<- function(X, N.total) # Density-dependence function

{

# Set parameter values

ALPHA <- X[1]; N <- X[2]

Amin <-1;Amax<- 50; Bmin <-0;Bmax<-0.9;a<- 20; BETA <-0.01

AA <- (ALPHA-Amin)/(Amax-Amin) # For convenience

S <- (Bmax-Bmin)*(1-AA)/(1þa*AA) # Survival

N <- N*(ALPHA*exp(-BETA*N.total)þS) # new population

N <- max(0,N) # N cannot be negative

return(N)

} # End of function

############## MAIN PROGRAM ##############

set.seed(10) # Initialize the random number seed

Maxgen <- 10000 # Number of generations run

Stats <- matrix(0,Maxgen,3) # Allocate space for statistics

MaxAlpha <- 50 # maximum value of alpha

Ninc <- 50 # Number of classes for alpha

# Allocate space to store data for each generation

Store <- matrix(0,Maxgen, Ninc)

# Allocate space for alpha class and population size

Data <- matrix(0,Ninc,2)

Data[24,2] <- 1 # Initial population size and alpha class

ALPHA <- matrix(seq(from¼1, to ¼MaxAlpha, length¼Ninc),Ninc,1)

# Set Alpha

Data[,1] <- ALPHA # Place alpha in 1st column

for (Igen in 1:Maxgen) # Iterate over generations

{

N.total <- sum(Data[,2]) # Total population size

Data[,2] <- apply(Data,1,DD.FUNCTION, N.total) # New cohort

Store[Igen,] <

- Data[,2] # Store values for this generation

Keep track of population size, mean trait value and SD of trait value

Stats[Igen,2] <- sum(Data[,1]*Data[,2])/sum(Data[,2]) # Mean

S <- sum(Data[,2]) # Population size

Stats[Igen,1] <- S # Population size

INVASIBILITY ANALYSIS 219

SX1 <- sum(Data[,1]^2*Data[,2])

SX2 <- (sum(Data[,1]*Data[,2]))^2/S

Stats[Igen,3] <- sqrt((SX1-SX2)/(S-1)) # SD of trait

# Introduce a mutant by picking a random integer between 1 and 50

Mutant <- ceiling(runif(1, min¼0, max¼50))

Data[Mutant,2] <- Data[Mutant,2]þ1 # Add mutant to class

} # End of Igen loop

par(mfrow¼c(3,2)) # Split graphics page into 3 x 2 panels

for (Row in 9998:Maxgen) # Select rows to be plotted

{

plot(ALPHA, Store[Row,], type¼’l’, xlab¼’Alpha’, ylab¼ ’Number’)

} # End of frequency polygon plots

Generation <- seq(from¼1, to¼Maxgen) # Vector of generations

N0 <- 9900 # Starting value for plots

plot(Generation[N0:Maxgen], Stats[N0:Maxgen,1], ylab¼’Popula-

tion size’,xlab¼’Generat ion’ , type¼’l’)

plot(Generation[N0:Maxgen], Stats[N0:Maxgen,2], ylab¼’Mean’,

xlab¼’Generation’, type¼’l’)

plot(Generation[N0:Maxgen], Stats[N0:Maxgen,3], ylab¼’SD’,

xlab¼’Generation’, type¼’l’)

print(c(’Mean alpha in last gen ¼ ’,Stats[Maxgen,2]))

print(c(’SD of alpha in last gen ¼ ’,Stats[Maxgen,3]))

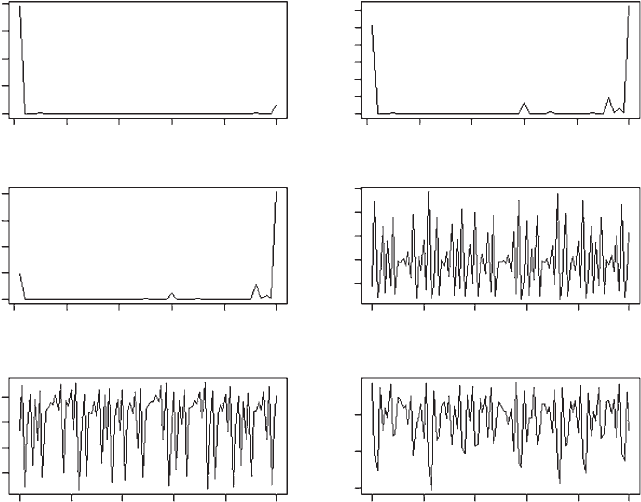
OUTPUT: (Figure 3.19)

Generation

9,900

0 40 80 120

20 40 60 80

100 300

10 20

Alpha

30 40 50

01020

Alpha

30 40 50 0 10 20

Alpha

30 40 50

200 600 1,000

15 20

Mean

Number

Population size

30 40

9,920 9,940 9,960 9,980 10,000

Generation

9,900 9,920 9,940 9,960 9,980 10,000

Generation

9,900 9,920 9,940 9,960 9,980 10,000

Figure 3.19 Results of multiple invasibility analysis of Scenario 6. The three frequency

polygons show results for generation 9,998, 9,999 and 10,000.

220 MODELING EVOLUTION

> print(c(’Mean alpha in last gen ¼ ’,Stats[Maxgen,2]))

[1] “Mean alpha in last gen ¼ ” “40.6067676012847”

> print(c(’SD of alpha in last gen ¼ ’,Stats[Maxgen,3]))

[1] “SD of alpha in last gen ¼ ” “17.8941418836399”

The frequency polygon plots for the last three generations show dramatic shifts in

the mean and modal values of . As indicated by the previous analyses, the

equilibrium from the pairwise invasibility analysis is highly unstable and is un-

likely to be ever attained, since any small deviations set the population into

extreme ﬂuctuations. The population consists of different clones, with their

frequencies changing through time.

3.9 Some exemplary papers

Katsukawa, Y., T. Katsukawa, and H. Matsuda. 2002. Indeterminate growth is

selected by a trade-off between high fecundity and risk avoidance in stochas-

tic environments. Population Ecology 44:265–272.

Problem: Optimal allocation of energy to growth, survival, and reproduction when

survival is temporally variable

Model type: Two age/stage

Density-dependence: None

Trade-off: Total allocation of energy to survival, growth, and reproduction ﬁxed

Analysis: Maximization of

Reference scenario: Scenario 1

Ebenman, B., A. Johansson, T. Jonsson, and U. Wennergren. 1996. Evolution

of stable population dynamics through natural selection. Proceedings of the

Royal Society of London – Series B: Biological Sciences 263:1145–1151.

Problem: Optimal combination of density-dependent parameters when population

dynamics can range from a ﬁxed equilibrium to chaotic

Model type: Two-stage

Density-dependence: Ricker function applied to maturation rate and juvenile

survival

Trade-off: Maturation rate and juvenile survival

Analysis: Invasibility analysis

Reference scenario: Scenarios 3 and 5

Lalonde, R. G. and B. D. Roitberg. 2006. Chaotic dynamics can select for long-

term dormancy. American Naturalist 168:127–131.

Problem: The optimal dormancy when population dynamics are chaotic

Model type: Up to 13 generations of dormancy

Density-dependence: Ricker function

Trade-off: No explicit trade-off

INVASIBILITY ANALYSIS 221

Analysis: Multiple invasibility analysis

Reference scenario: Scenarios 3 and 6

Johst, K., M. Doebeli, and R. Brandl . 1999. Evolution of complex dynamics in

spatially structured populations. Proceedings of the Royal Society of London –

Series B: Biological Sciences 266:1147–1154.

Problem: The optimal density-dependent and density-independent dispersal rates

Model type: One generation per time step

Density-dependence: Fecundity varies with density using an equation that can take a

variety of shapes

Trade-off: No explicit trade-offs

Analysis: Multiple invasibility analysis

Reference scenario: Scenarios 3 and 6

Benton, R. A. and A. Grant. 1999. Optimal reproductive effort in stochastic,

density-dependent environments. Evolution 53:677–688.

Problem: Optimal reproductive effort

Model type: Two age/stage class

Density-dependence: Various

Trade-off: Various combinations of reproductive effort and survival at age with or

without temporal variation

Analysis: Elasticity analysis

Reference scenario: Scenario 4

Wilbur, H. M. and V. H. W. Rudolf. 2006. Life-history evolution in uncertain

environments: Bet hedging in time. American Naturalist 168:398–411.

Problem: Optimal iteroparity and delayed maturity in a stochastic environment

Model type: Two-stage

Density-dependence: Ricker function applied to fertility with parameters selected to

ensure a stable population in a deterministic environment

Trade-off: Adult survival and clutch size in some model variants

Analysis: Invasibility analysis

Reference scenario: Scenarios 4 and 5

White, A., J. V. Greenman, T. G. Benton, and M. Boots. 2006. Evolutionary

behaviour in ecological systems with trade-offs and non-equilibrium popula-

tion dynamics. Evolutionary Ecology Research 8:387–398.

Problem: Optimal reproductive effort when population dynamics are complex

Model type: No explicit age structure

Density-dependence: Ricker function

Trade-off: Density-independent fecundity and survival

Analysis: Invasibility analysis

Reference scenario: Scenario 6

222 MODELING EVOLUTION

CHAPTER 4

Genetic Models

4.1 Introduction

The “Fisherian” optimality approach determines the optimal combination of trait

values but not the evolutionary trajectory nor, in general, the variation to be

expected about the optimal combination. Invasibility analysis is also primarily

concerned with the Evolutionarily Stable Strategy (ESS) values; though assuming

clonal inheritance, it can give insight into the temporal evolution of trait values.

Whether such analyses can be extended to organisms with other modes of inheri-

tance is not clear, though the analysis presented in Scenario 5 of this chapter

suggests that caution is warranted in applying the results of invasibility analysis to

sexually reproducing organisms.

There are basically three ways to implement a genetic model, which I shall refer

to as (a) the population variance components approach, ( b) the individual variance

components approach, and (c) the individual locus approach. The ﬁrst two are

primarily for quantitative genetic modeling whereas the last can be used for both

quantitative genetic modeling and modeling simple Mendelian inheritance (e.g.,

single locus). The advantages of an individual-based model (IBM) are that it is easy

to incorporate complex population dynamics, frequency-dependence, and func-

tional constraints. IBMs are, however, relatively computer-intensive (particularly

individual locus models).

4.1.1 Population variance components (PVC) models

Rather than focus upon individual loci this method tackles the problem by focus-

ing at the population level upon the variances and covariances of the traits. The

phenotypic value, X, of a trait can be decomposed into the sum of genetic, G, and

environmental, E, components:

X ¼ G þ E ð4:1Þ

where it is assumed that G and E are uncorrelated and normally distributed, the

latter with a zero mean. The phenotypic variance, s

is thus also composed of the

sum of the genetic, s

, and the environmental, s

, variances

¼ s

þ s

ð4:2Þ

The genetic variance can itself be broken down into additive, dominance, and

epistatic components, but I shall ignore the latter two, as is typically done.

Heritability is a measure of the extent to which the resemblance between rela-

tives is due to additive genetic effects. A simple way to estimate heritability is to

regress the average trait value of offspring on the mid-parent value. Provided that

there are no maternal (or paternal) effects or environmental effects due to simi-

larity in the rearing environment within but not among families, the slope of this

regression is equal to the heritability of the trait. The general deﬁnition of herita-

bility, h

, is the ratio of additive genetic variance to phenotypic variance:

ð4:3Þ

Heritability measures the proportion of the total variance that can be ascribed to the

additive effect of genes. A zero heritability means that variation is entirely environ-

mental whereas a heritability of one means that the variation is entirely due to

the additive effects of genes. The general relationship between offspring and par-

ents is

Offspring

¼ð1  h

Þm

Population

þ h

Parents

ð4:4Þ

where m refers to the mean values. Under directional selection the mean value of

parents is greater or less that of the population, depending on the direction of

selection, and by rearranging equation 4.4 we get the response to the selection as

Offspring

 m

Population

¼ h

ðm

Parents

 m

Offspring

R ¼ h

S ¼

ð4:5Þ

where S is the selection differential. The above equation is referred to as the

Breeder’s equation. It is frequently more convenient to write S in terms of

phenotypic standard deviations:

S ¼ is

ð4:6Þ

where i is called the selection intensity,

i ¼

ð4:7Þ

P is the proportion selected for each generation and z is the ordinate at the point of

truncation. Suppose we wish to apply truncation selection by selecting the top P

proportion of the population, the selection intensity can be calculated using the

following R code:

Vp <- 1 # Phenotypic variance

P <- 0.2 # Proportion selected

x <- -qnorm(P, mean ¼ 0, sd ¼ 1) # x value

z <- exp(-0.5*x^2)/(sqrt(2*pi)) # z

224 MODELING EVOLUTION

i <- z/P # Selection intensity

S <- i*sqrt(Vp) # Selection differential

The change per generation is a constant and hence a plot of mean trait value on

generation will give a straight line (i.e., m

tþ1

¼ m

þ h

S).

In nature, selection is likely to be generally stabilizing rather than directional.

Two functions often used for such a scenario are a quadratic ﬁtness function and a

Gaussian ﬁtness function. Under the latter function the ﬁtness of a trait, W, can be

written as

W ¼ e



ðxyÞ



ð4:8Þ

where y is the value at which ﬁtness is maximized and o is a measure of the

strength of stabilizing selection, the strength of selection decreasing with increas-

ing o. Stabilizing selection can be incorporated into the single trait model as

o þ s

ðy  m

Population;t

Þð4:9Þ

Note that the response to selection is now a function of the distance from the

optimum value and hence is a function of generation. Over time the population

moves smoothly to the optimum value.

Extension of the above model to multiple traits requires the introduction of the

correlation between traits. Correlations can arise because genes may affect several

traits (called pleiotropy), be associated because of linkage or because of environ-

mental factors. Assuming, as is generally done, that the environmental and genet-

ic covariances are independent we can break the phenotypic covariance between

traits X and Y, s

PXY

, into the sum of the two covariances:

PXY

¼ s

GXY

þ s

EXY

ð4:10Þ

Noting that a correlation, r, is equal to

r ¼

ð4:11Þ

the phenotypic correlation can be obtained from the above relationship as

PXY

¼ r

þ r

¼ r

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ r

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ð1  h

Þð1  h

ð4:12Þ

For multiple traits the Breeder’s equation can be expanded using matrix nota-

tion as

D z



¼ GP

1

S ð4:13Þ

where is D



z the vector of changes in trait means, G is the additive genetic variance–

covariance matrix, P is the phenotypic variance–covariance matrix, S is the vector of

GENETIC MODELS 225

selection differentials, and the 1 means the matrix inverse. For two traits, labeled 1

and 2, equation (4.13) can be written in explicit matrix format as





G12

G21



P12

P21



1



ð4:14Þ

The diagonal elements of the genetic and phenotypic matrices hold the variances

and the off-diagonals the covariances (note that the matrices are symmetrical and

hence s

¼ s

). The response to directional truncation selection is the same as in

the single trait model, in that both traits change by a ﬁxed amount per generation,

though in this case the amount is a function of the selection differential and the

correlation between the traits.

To set the values in equation (4.14) it is generally easier to commence with the

heritabilities, phenotypic variances, and correlations, and then make use of

equations (4.3) and (4.12). For two traits the coding is simple: for example,

h2 <- c(0.2,0.4) # Set heritabilities

Vp <- c(1,2) # Set phenotypic variances

Rp <- 0.4 # Set phenotypic correlation

Ra <- 0.15 # Set genetic correlation

Va <- h2*Vp # Using h2 ¼Va/Vp

Covp <- Rp*sqrt(Vp[1]*Vp[2]) # Using r ¼ Cov/SD1SD2

Cova <- Ra*sqrt(Va[1]*Va[2]) # Using r ¼ Cov/SD1SD2

Gmatrix <- matrix( c(Va[1],Cova, Cova, Va[2]),2,2) # G matrix

Pmatrix <- matrix(c(Vp[1],Covp, Covp, Vp[2]),2,2) # P matrix

The environmental correlation must lie between 1andþ1, which is not

guaranteed by the above coding. It is therefore necessary to put in a check,

using equation (4.12) and stop the program if r

falls outside the permissible

limits:

# Check that Re is possible

Re <- (Rp-Ra*sqrt(h2[1]*h2[2]))/sqrt((1-h2[1])*(1-h2[2]))

if(abs(Re) >1 ) stop (c(“problem with Re”))

The value of the heritability is unlikely to matter in terms of the ﬁnal equilibrium

but will certainly affect the time taken to reach this value, should it exist, and the

variation about the value.

With more than two traits the above coding can be tedious but it can be

replaced by the following more general code. Suppose we have three traits. First

we construct a matrix, which I have called H2, which holds the heritabilities on

the diagonal, the genetic correlations above the diagonal and the phenotypic

correlations below the diagonal. We then use this matrix in conjunction with

the phenotypic variances (assumed to be 1.5, 1.0, and 0.5 in the example below) to

construct the necessary covariance matrices:

226 MODELING EVOLUTION

NX <- 3 # Number of traits

# Matrix of heritabilities and correlations.

# Values in bold are the heritabilities

# Genetic correlations are above the diagonal, phenotypic correl-

ations below

H2 <- matrix (c (0.4, 0.7, 0.3,

0.6, 0.5, 0.1,

0.4, 0.6, 0.3), NX, NX, byrow¼TRUE)

# Construct the Phenotypic Covariance matrix

# Note that initial covariances are set to 1 (arbitrary)

CovP <- matrix (1, NX, NX) # Phenotypic variances

diag(CovP) <- c (1.5,1.0,0.5)# Sets diagonal elements ¼variances

# Establish CovA from h2 and CovP and CovE from CovA and CovP

CovA <- matrix (0, NX, NX) # Allocate space

CovE <- matrix (0, NX, NX) # Allocate space

for ( i in 1:NX) # Iterate over cells

{

CovA[i,i] <- CovP[i,i]*H2[i,i] # ¼ Vp*h2

CovE[i,i] <- CovP[i,i]-CovA[i,i] # Variances

# Check that environmental variance is positive

if (CovE[i,i] < 0) stop (c(“Problem with CovE”))

}

# Phenotypic and genetic covariances

N. minus. 1 <- NX-1

for ( i in 1:N.minus.1)

{

jj <-iþ1

for (j in jj:NX)

{

# Phenotypic covariances

CovP [i,j] <- H2[j,i]*sqrt (CovP[i,i]*CovP[j,j])

CovP[j,i] <- CovP[i,j]

CovA[i,j] <- H2[i,j]*sqrt (CovA[i,i]*CovA[j,j]) # Ra*sqrt (VaxVay)

CovA j,i] <- CovA [i,j]

CovE[i,j] <- CovP [i,j]-CovA[i,j] # By difference

CovE[j,i] <- CovE [i,j]

}

Stabilizing selection can be incorporated using a third matrix (Lande 1980),



z¼ GðW þ PÞ

1

Sðm  uÞð4:15Þ

where W is a positive semideﬁnite matrix, m is a vector of trait means, and y is a

vector of optimal trait values. The diagonal elements of W are measures of the

strength of stabilizing selection acting directly on the character (e.g., o in

GENETIC MODELS 227