Robertson C.R. Fundamental electrical and electronic principles
Подождите немного. Документ загружается.


D.C. Transients 261
Assignment Questions
1 A 4 7 μ F capacitor is connected in series with
a 39 k resistor, across a 24 V d.c. supply.
Calculate (a) the circuit time constant, (b) the
values for initial and nal charging current,
and (c) the time taken for the capacitor to
become fully charged.
2 A 150 mH inductor of resistance 50 is
connected to a 50 V d.c. supply. Determine
(a) the initial rate of change of current, (b) the
nal steady current, and (c) the time taken for
the current to change from zero to its nal
steady value.
3 An inductor of negligible resistance and of
inductance 0.25 H, is connected in series with a
1. 5 k resistor, across a 24 V d.c. supply. Calculate
the current owing after one time constant.
4 A 5 H inductor has a resistance R ohm.
This inductor is connected in series with
a10 resistor, across a 140 V d.c. supply. If
the resulting circuit time constant is 0.4 s,
determine (a) the value of the coil resistance,
and (b) the nal steady current.
5 D e ne the time constant of a capacitor-resistor
series circuit.
Such a circuit comprises a 50 μ F capacitor and
a resistor, connected to a 100 V d.c. supply via
a switch. If the circuit time constant is to be
5 s, determine (a) the resistor value, (b) the
initial charging current.
6 The dielectric of a 20 μ F capacitor has a
resistance of 65 M . This capacitor is fully
charged from a 120 V d.c. supply. Calculate
the time taken, after disconnection from
the supply, for the capacitor to become fully
discharged.
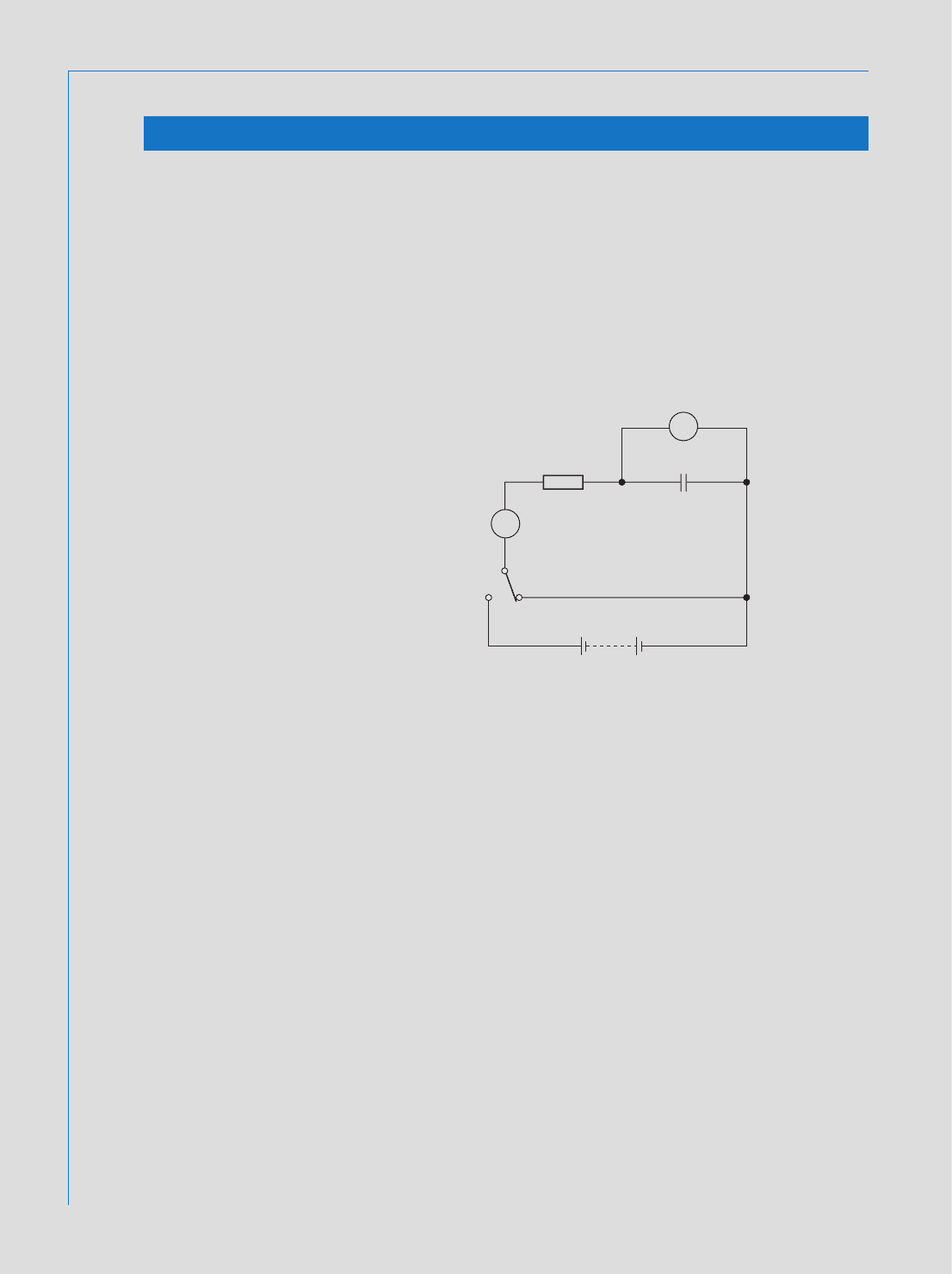
262 Fundamental Electrical and Electronic Principles
Suggested Practical Assignments
V
A
10 μF
10 MΩ
250 V
‘1’ ‘2’
Fig. 8.18
Assignment 1
To investigate the variation of capacitor voltage and current during charge and
discharge cycles.
Apparatus:
1 10 μ F capacitor
1 10 M resistor
1 2-pole switch
1 d.c. power supply
1 ammeter (microammeter)
1 DVM (with highest possible input resistance)
1 stopwatch
1 Connect the circuit of Fig. 8.18 , and adjust the psu output to 250 V.
2 Simultaneously move the switch to position ‘ 1 ’ and start the stopwatch.
3 Record the circuit current and capacitor p.d. at 10 s intervals, for the rst 60 s.
4 Continue recording the current and voltage readings, at 20 s intervals, for a
further 4 minutes. Reset the stopwatch to zero. Reverse the connections to
the ammeter.
5 Move the switch back to position ‘ 2 ’ , and repeat the procedures of
paragraphs (3) and (4) above.
6 Plot graphs of current and capacitor p.d., versus time, for both the charging
and discharging cycles.
7 Submit a complete assignment report, which should include the following:
(i) The comparison of the actual time constant (determined from the
plotted graphs) to the theoretical value. Explain any discrepancy found.
(ii) Explain why both the charging and discharging currents tend to ‘ level
o ’ at some small value, rather than continuing to decrease to zero.
Method:

Semiconductor Theory
and Devices
Chapter 9
Learning Outcomes
This chapter explains the behaviour of semiconductors and the way in which they are
employed in diodes.
On completion of this chapter you should be able to:
1 Understand the way in which conduction takes place in semiconductor materials.
2 Understand how these materials are employed to form devices such as diodes.
3 Understand the action of a zener diode and perform basic calculations involving a simple
regulator circuit.
263
9.1 Atomic Structure
In Chapter 1 it was stated that an atom consists of a central nucleus
containing positively charged protons, and neutrons, the latter being
electrically neutral, surrounded by negatively charged electrons
orbiting in layers or shells. Electrons in the inner orbits or shells
have the least energy and are tightly bound into their orbits due to
the electrostatic force of attraction between them and the nucleus.
Electrons in the outermost shell experience a much weaker binding
force, and are known as valence electrons.
In conductors it is these valence electrons that can gain suffi cient
energy to break free from their parent atoms. They thus become
‘ free ’ electrons which are available to drift through the material under
the infl uence of an emf and hence are mobile charge carriers which
produce current fl ow.
The shells are identifi ed by letters of the alphabet, beginning with the
letter K for the innermost shell, L for the next and so on. Each shell
represents a certain energy level, and each shell can contain only up to a

264
Fundamental Electrical and Electronic Principles
certain maximum number of electrons. This maximum possible number
of electrons contained in a given shell is governed by the relationship
2n
2
, where n is the number of the shell. Thus the maximum number of
electrons in the fi rst four shells will be as shown in Table 9.1 .
Table 9.1
Shell n Max. No. of
electrons
K12 1
2
2
L22 2
2
8
M32 3
2
18
N42 4
2
32
Table 9.2
Shell L M N
Subshell 2s 2p 3s 3p 3d 4s 4p 4d 4f
Max. No. 262610261014
Total 818 32
All things in nature tend to stabilise at their lowest possible energy
level, and atoms and electrons are no exception. This results in the
lowest energy levels (shells) being fi lled fi rst until all the electrons
belonging to that atom are accommodated. Another feature of the
system is that if the outermost shell of an atom is completely full
(contains its maximum permitted number of electrons) then the binding
force on these valence electrons is very strong and the atom is very
stable. To illustrate this consider the inert gas neon. The term inert is
used because it is very diffi cult to make it react to external infl uences.
A neon atom has a total of 10 electrons, two of which are in the K
shell and the remaining eight completely fi ll the L shell. Having a full
valence shell is the reason why neon, krypton and xenon are inert gases.
In contrast, a hydrogen atom has only one electron, so its valence shell
is almost empty and it is a highly reactive element. One further point
to bear in mind is that the electrons in the shells (from L onwards)
may exist at slightly different energy levels known as subshells. These
subshells may also contain only up to a certain maximum number of
electrons. This is shown, for the L, M and N shells, in Table 9.2 .
9.2 Intrinsic (Pure) Semiconductors
Semiconductors are group 4 elements, which means they have four
valence electrons. For this reason they are also known as tetravalent

Semiconductor Theory and Devices
265
elements. Among this group of elements are carbon (C), silicon (Si),
germanium (Ge) and tin (Sn). Of these only silicon and germanium
are used as intrinsic semiconductors, with silicon being the most
commonly used. Carbon is not normally considered as a semconductor
because it can exist in many different forms, from diamond to graphite.
Similarly, tin is not used because at normal ambient temperatures it
acts as a good conductor. The following descriptions of the behaviour
of semiconductor materials will be confi ned to silicon although the
general properties and behaviour of germanium are the same. The
arrangement of electrons in the shells and subshells of silicon are
shown in Table 9.3 .
Table 9.3
KL M
1s 2s 2p 3s 3p 3d
22622—
From Table 9.3 it may be seen that the four valence electrons are
contained in the M shell, where the 3 s subshell is full but the 3p
subshell contains only two electrons. However, from Table 9.2 it can
be seen that a 3p subshell is capable of containing up to a maximum of
six electrons before it is full, so in the silicon atom there is space for a
further four electrons to be accommodated in this outermost shell.
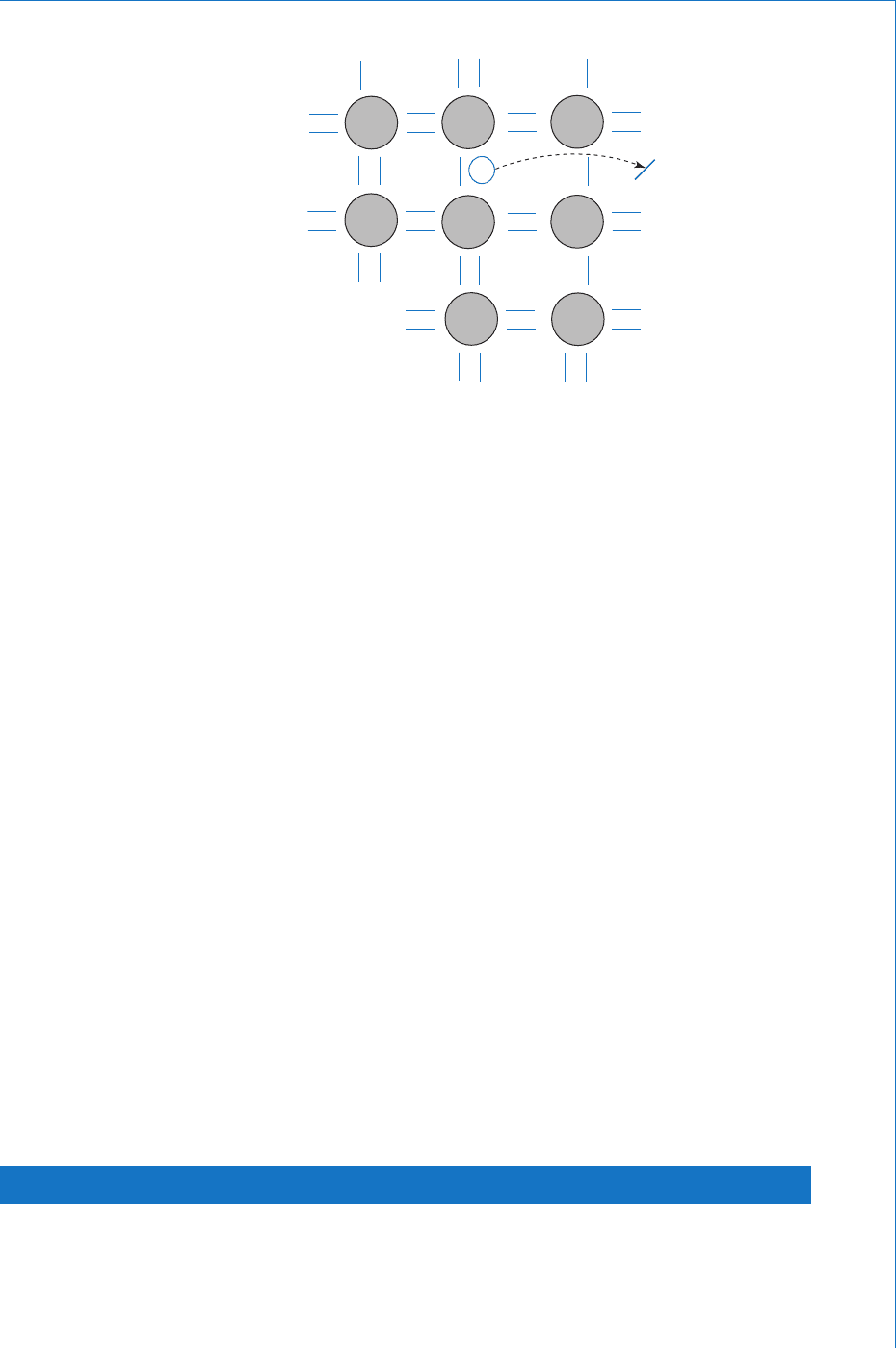
Silicon has an atomic bonding system known as covalent bonding
whereby each of the valence electrons orbits not only its ‘ parent ’ atom,
but also orbits its closest neighbouring atom. This effect is illustrated
in Fig. 9.1 , where the fi ve large circles represent the nucleus and shells
K and L of fi ve adjacent atoms (identifi ed as A, B, C, D and E) and the
small circles represent their valence electrons, where the letters a, b, c
etc. identify their ‘ parent ’ atoms.
Concentrating on the immediate space surrounding atom A, it may be
seen that there are actually eight valence electrons orbiting this atom;
four of its own plus one from each of its four nearest neighbours. This
fi gure is only two-dimensional and is centred on atom A. However, the
same arrangement would be found if the picture was centred on any given
atom in the crystal lattice. In addition, the actual lattice is of course three-
dimensional. In this case imagine atom A being located at the centre of
an imaginary cube with the other four neighbouring atoms being at four
of the corners of the cube. Each of these ‘ corner ’ atoms is in turn at the
centre of another imaginary cube, and so on throughout the whole crystal
lattice. The result is what is known as the diamond crystal lattice.
From the above description it may be seen that each silicon atom has
an apparent valency of 8, which is the same as for the inert gases

266
Fundamental Electrical and Electronic Principles
such as neon. The covalent bonding system is a very strong one so the
valence electrons are quite tightly bound into it. It is for this reason that
intrinsic silicon is a relatively poor conductor of electrical current, and
is called a semiconductor.
9.3 Electron-Hole Pair Generation and Recombination
Although the covalent bond is strong, it is not perfect. Thus, when
a sample of silicon is at normal ambient temperature, a few valence
electrons will gain suffi cient energy to break free from the bond and so
become free electrons available as mobile charge carriers. Whenever
such an electron breaks free and drifts away from its parent atom it
leaves behind a space in the covalent bond, and this space is referred
to as a hole. Thus, whenever a bond is broken an electron-hole pair
is generated. This effect is illustrated in Fig. 9.2 , where the short
straight lines represent electrons and the small circle represents a
corresponding hole. The large circles again represent the silicon atoms
complete with their inner shells of electrons.
The atom which now has a hole in its valence band is effectively a
positive ion because it has lost an electron which would normally
occupy that space. On the atomic scale, the ion is very massive,
is locked into the crystal lattice, and so cannot move. However,
electron-hole pair generation will be taking place in a random manner
throughout the crystal lattice, and a generated free electron will at
D
A
B
a
a
e
d
a
a
b
c
E
C
Fig. 9.1
Semiconductor Theory and Devices
267
some stage drift into the vicinity of one of these positive ions, and be
captured, i.e. the hole will once more be fi lled by an electron. This
process is known as recombination, and when it occurs the normal
charge balance of that atom is restored.
The hole-pair generation and recombination processes occur
continuously, and since heat is a form of energy, will increase as the
temperature increases. This results in more mobile charge carriers being
available, and accounts for the fact that semiconductors have a negative
temperature coeffi cient of resistance, i.e. as they get hotter they conduct
more easily. It must be borne in mind that although these thermally
generated mobile charge carriers are being produced, the sample of
material as a whole still remains electrically neutral. In other words, if a
‘ head count ’ of all the positive and negative charged particles could be
made, there would still be a balance between positive and negative, i.e.
for every free electron there will be a corresponding hole.
The concept of the drift of free electrons through the material may be
readily understood, but the concept of hole mobility is more diffi cult to
appreciate. In fact the holes themselves cannot move — they are merely
generated and fi lled. However, when a bond breaks down the electron
that drifts away will at some point fi ll a hole elsewhere in the lattice.
Thus the hole that has been fi lled is replaced elsewhere by the newly
generated hole, and will appear to have drifted to a new location. In
order to simplify the description of conduction in a semiconductor, the
holes are considered to be mobile positive charge carriers whilst the
free electrons are of course mobile negative charge carriers.
9.4 Conduction in Intrinsic Semiconductors
Figure. 9.3 illustrates the effect when a source of emf is connected
across a sample of pure silicon. The electric fi eld produced by
Si
Si
Si
Si
Si
Si
Si
Si
free electron
hole
Fig. 9.2
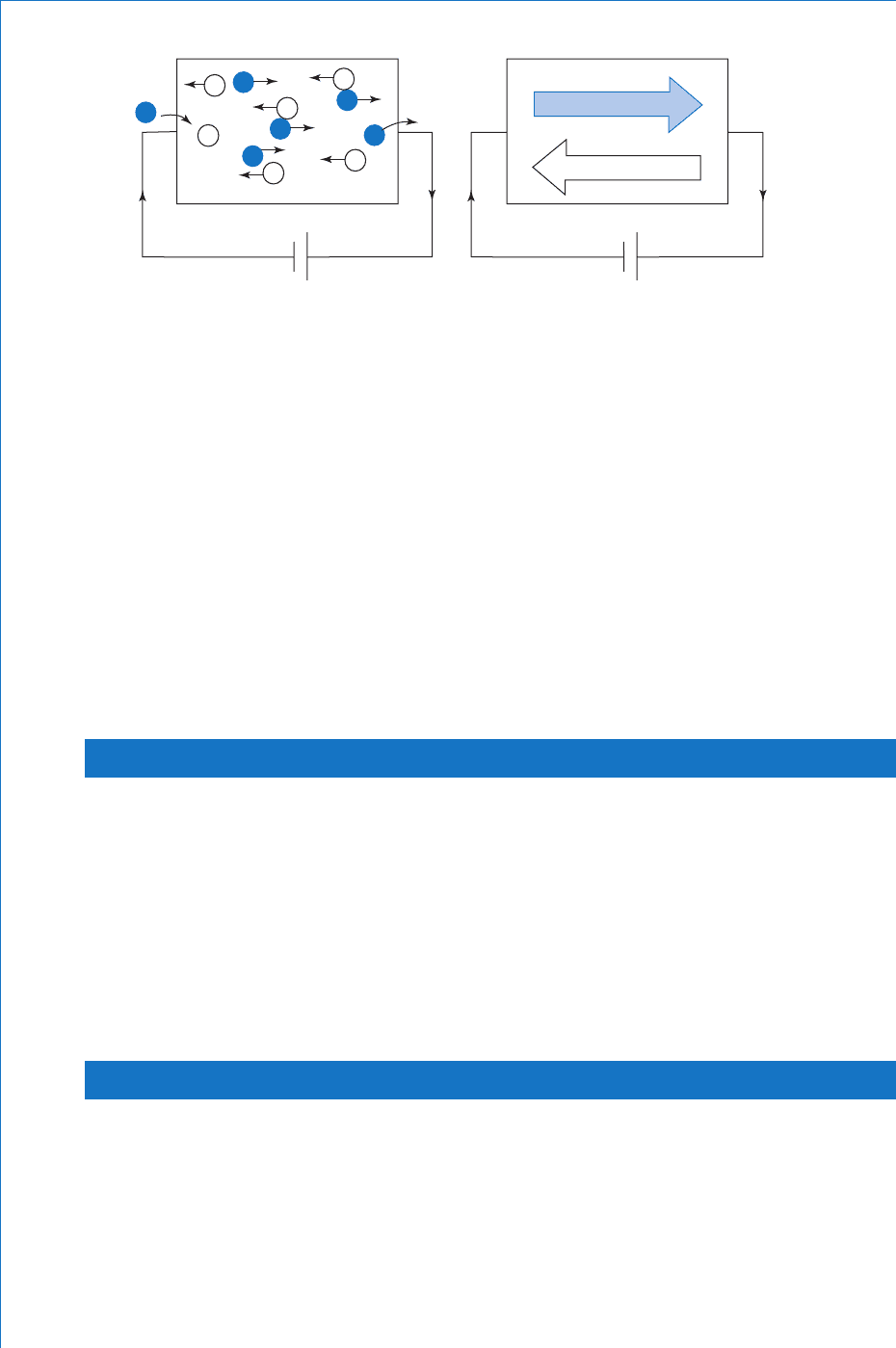
268
Fundamental Electrical and Electronic Principles
the battery will attract free electrons towards the positive plate
and the corresponding holes towards the negative plate. Since the
external circuit is completed by conductors, and holes exist only
in semiconductors, then how does current actually fl ow around the
circuit without producing an excess of positive charge (the holes) at
the left-hand end of the silicon? The answer is quite simple. For every
electron that leaves the right-hand end and travels to the positive plate
of the battery, another is released from the negative plate and enters
the silicon at the left-hand end, where a recombination can occur. This
recombination will be balanced by fresh electron-hole pair generation.
Thus, within the silicon there will be a continuous drift of electrons
in one direction with a drift of a corresponding number of holes in the
opposite direction. In the external circuit the current fl ow is of course
due only to the drift of electrons.
9.5 Extrinsic (Impure) Semiconductors
Although pure silicon and germanium will conduct, as explained in
the previous section, their characteristics are still closer to insulators
than to conductors. In order to improve their conduction very small
quantities (in the order of 1 part in 10
8
) of certain other elements are
added. This process is known as doping. The impurity elements that
are added are either pentavalent (have fi ve valence electrons) or are
trivalent (have three valence electrons) atoms. Depending upon which
type is used in the doping process determines which one of the two
types of extrinsic semiconductor is produced.
9.6 n-type Semiconductor
To produce this type of semiconductor, pentavalent impurities are
employed. The most commonly used are arsenic (As), phosphorus (P),
and antimony (Sb). When atoms of such an element are added to the
silicon a bonding process takes place such that each impurity atom
joins the covalent bonding system of the silicon. However, since each
impurity atom has fi ve valence electrons, one of these cannot fi nd a
place in a covalent bond. These ‘ extra ’ electrons then tend to drift
I
electrons
holes
I
(electrons)
Fig. 9.3
Semiconductor Theory and Devices
269
away from their parent atoms and become additional free electrons in
the lattice. Since these impurities donate an extra free electron to the
material they are also known as donor impurities.
As a consequence of each donor atom losing one of its valence electrons,
they become positive ions locked into the crystal lattice. Note that free
electrons introduced by this process do not leave a corresponding hole,
although thermally generated electron-hole pairs will still be created in
the silicon. The effect of the doping process is illustrated in Fig. 9.4 .
Si
Si
Si
Si
Si
Si
Si
P
5
th
‘free’
electron
Fig. 9.4
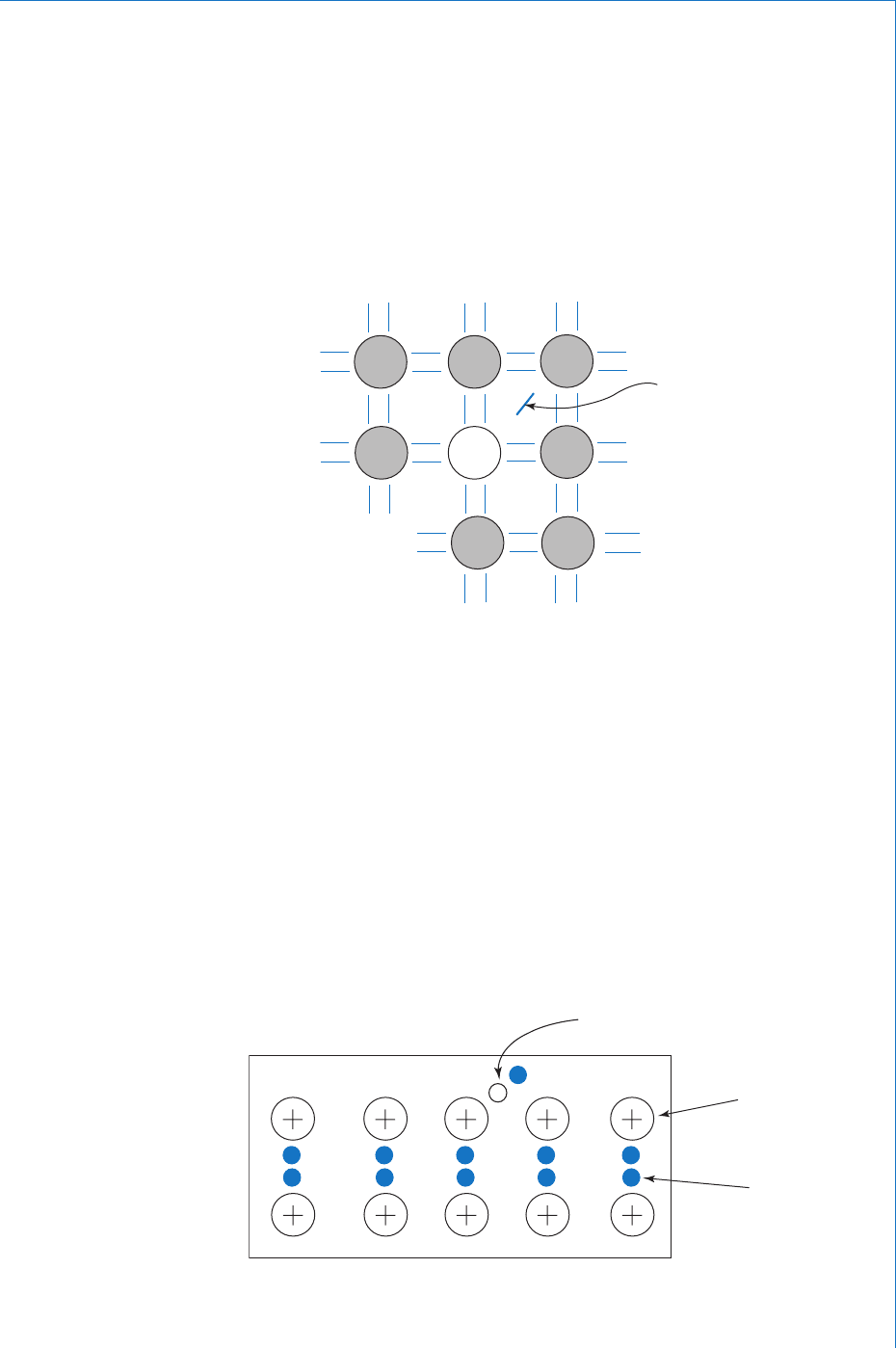
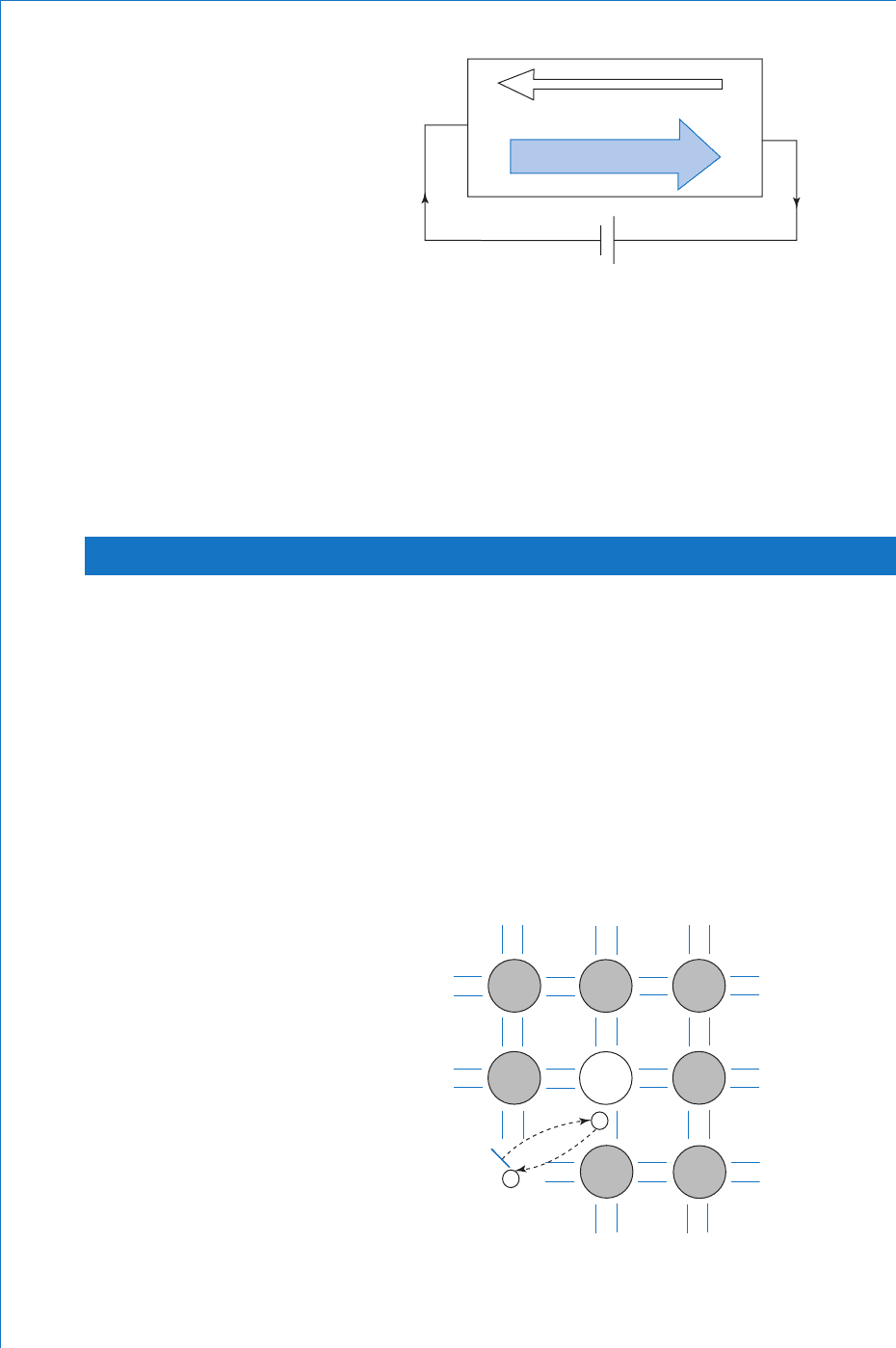
Since the extra charge carriers introduced by the impurity atom are
negatively charged electrons, and these will be in addition to the
electron-hole pairs, then there will be more mobile negative charge
carriers than positive, which is why the material is known as n-type
semiconductor. In this case the electrons are the majority charge
carriers and the holes are the minority charge carriers. It should again
be noted that the material as a whole still remains electrically neutral
since for every extra donated free electron there will be a fi xed positive
ion in the lattice. Thus a sample of n-type semiconductor may be
represented as consisting of a number of fi xed positive ions with a
corresponding number of free electrons, in addition to the thermally
generated electron-hole pairs. This is shown in Fig. 9.5 .
e–h pair
fixed
positive
ion
free
electron
Fig. 9.5
270
Fundamental Electrical and Electronic Principles
The circuit action when a battery is connected across the material
is illustrated in Fig. 9.6 . Once more, only electrons fl ow around
the external circuit, whilst within the semiconductor there will be
movement of majority carriers in one direction and minority carriers
in the opposite direction.
9.7 p-type Semiconductor
In this case a trivalent impurity such as aluminium (Al), gallium
(Ga), or indium (In) is introduced. These impurity atoms also join
the covalent bonding system, but since they have only three valence
electrons there will be a gap or hole in the bond where an electron
would normally be required. Due to electron-hole pair generation in
the lattice, this hole will soon become fi lled, and hence the hole will
have effectively drifted off elsewhere in the lattice. Since each impurity
atom will have accepted an extra electron into its valence band they
are known as acceptor impurities, and become fi xed negative ions. The
result of the doping process is illustrated in Fig. 9.7 .
Si
Si
Si
Si
Si
Si
Si
Al
e–h
pair
Fig. 9.7
holes
electrons
I
Fig. 9.6
