Robertson C.R. Fundamental electrical and electronic principles
Подождите немного. Документ загружается.

D.C. Transients
251
Having confi rmed the initial and fi nal values for the transients, we now
need to consider how they vary, with time, between these limits. It has
already been stated that the variations will be non-linear (i.e. not
a straight line graph). In fact the variations follow an exponential law.
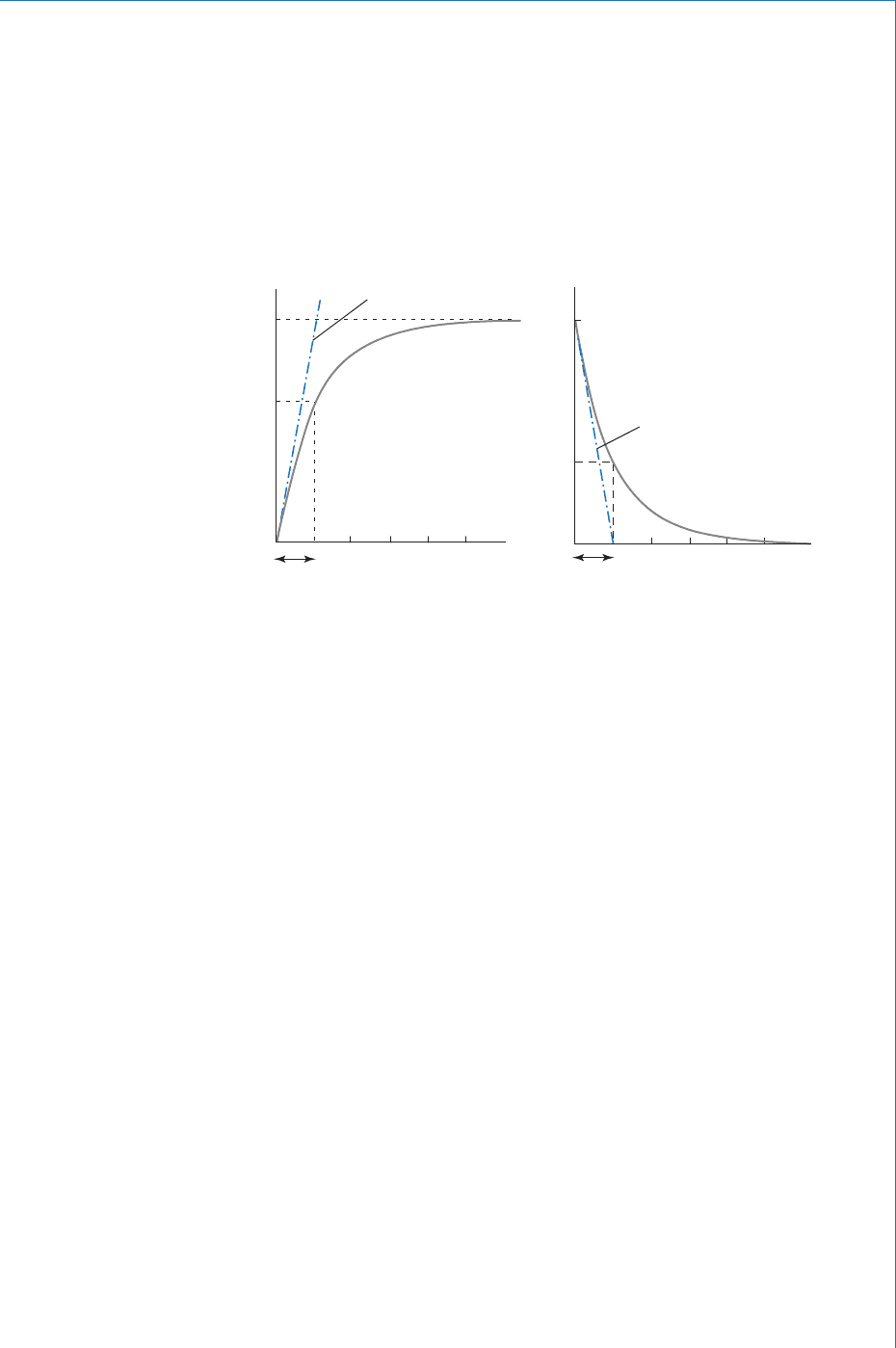
Any quantity that varies in an exponential fashion will have a graph
like that shown in Fig. 8.2(a) if it increases with time, and as in
Fig. 8.2(b) for a decreasing function.
Fig. 8.2
τ
2τ 3τ 4τ 5τ
t(s)0
0.632
X
X
initial rate of change
(a)
τ
2τ 3τ 4τ 5τ
t(s)0
0.368
X
0
X
initial rate of change
(b)
In Fig. 8.2(a) , X represents the fi nal steady state value of the variable x,
and in Fig. 8.2(b) , X
0
represents the initial value of x . In each case the
straight line (tangent to the curve at time t 0) indicates the initial rate
of change of x . The time interval shown as shown on both graphs is
known as the time constant, which is defi ned as follows:
The time constant is the time that it would take the variable to reach its
fi nal steady state if it continued to change at its initial rate.
From the above Figures it can be seen that for an increasing
exponential function, the variable will reach 63.2% of its fi nal value
after one time constant, and for a decreasing function it will fall to
36.8% of its initial value after seconds.
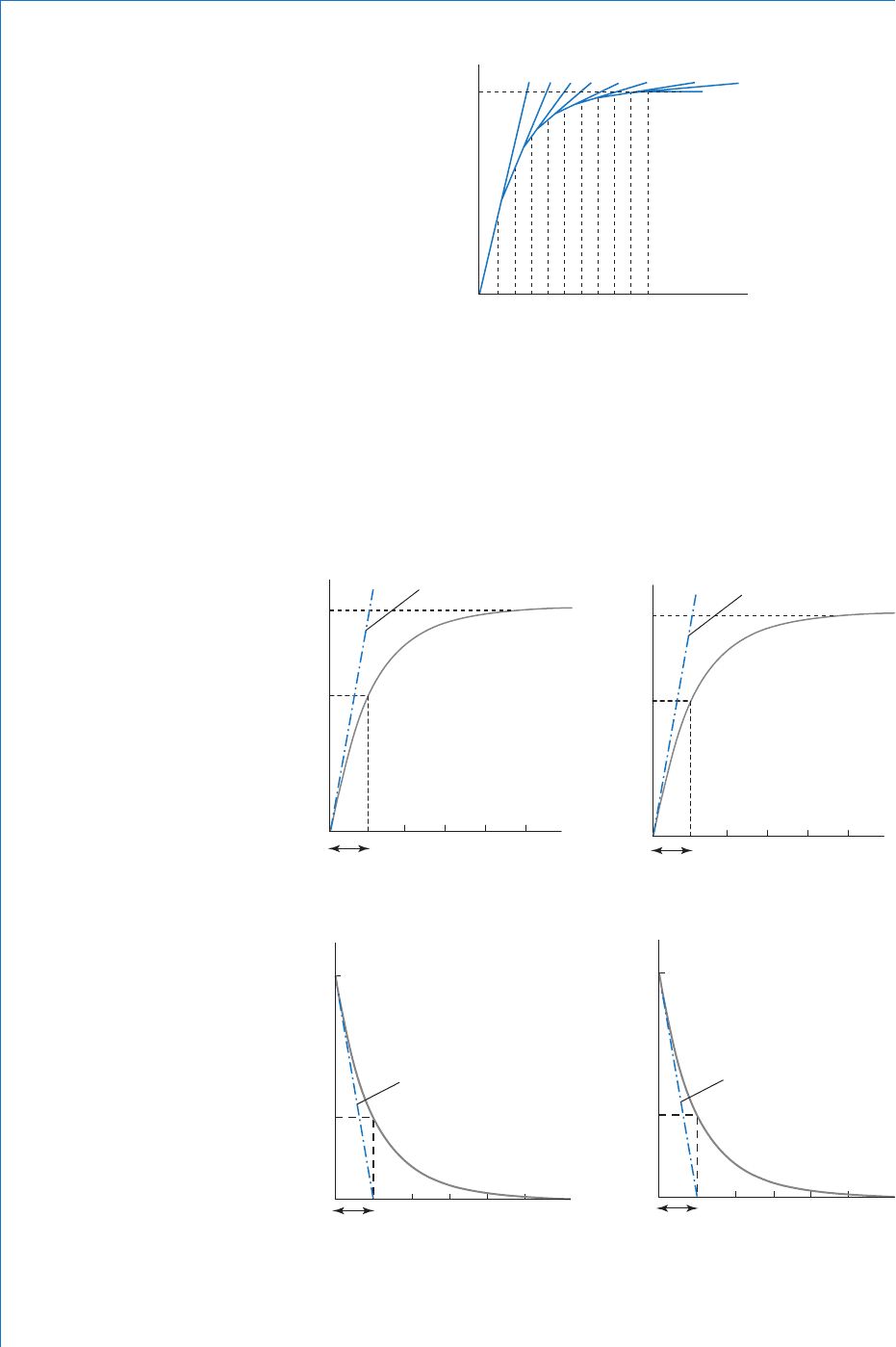
Note: Considering any point on the graph, it would take one time
constant for the variable to reach its fi nal steady value if it continued to
change at the same rate as at that point. Thus an exponential graph may
be considered as being formed from an infi nite number of tangents,
each of which represents the slope at a particular instant in time. This
is illustrated in Fig. 8.3 .
Also, theoretically, an exponential function can never actually reach
its fi nal steady state. However, for practical purposes it is assumed
that the fi nal steady state is achieved after 5 time constants. This is
justifi able since the variable will be within 0.67% of the fi nal value
after 5 seconds. So for Fig. 8.2(a) , after 5 seconds, x 0.9973 X.
252
Fundamental Electrical and Electronic Principles
Considering the circuit of Fig. 8.1 , assuming that the capacitor is fully
discharged, let the switch be moved to position ‘ B ’ . The capacitor will
now charge via resistor R until the p.d. between its plates, v
C
E volts.
Once fully charged, the circuit current will be zero. The variations of
capacitor voltage and charge, p.d. across the resistance and charging
current are shown in Figs. 8.4 to 8.7.
τ
2τ 3τ 4τ 5τ
t(s)0
0.368 I
0
I
0
i (A)
initial rate of change
Fig. 8.7
τ
2τ 3τ 4τ 5τ
t(s)0
E
V
R
(V)
0.386 E
initial rate of change
Fig. 8.6
τ
2τ 3τ 4τ 5τ
t(s)0
0.632 E
E
initial rate of change
V
c
(V)
Fig. 8.4
τ
2τ 3τ 4τ 5τ
t(s)0
0.632 Q
Q
initial rate of change
q (C)
Fig. 8.5
0
X
X
τ 2τ 3τ 4τ 5τ t(s)
Fig. 8.3

D.C. Transients
253
For such a CR circuit the time constant, (Greek letter tau), is CR
seconds. It may appear strange that the product of capacitance and
resistance yields a result having units of time. This may be justifi ed by
considering a simple dimensional analysis, as follows.
C
Q
V
It
V
R
V
I
CR
It
V
V
I
t
and
so, seconds
Hence, seconds CR (8.2)
Worked Example 8.1
Q A n 8 μ F capacitor is connected in series with a 0.5 M resistor, across a 200 V d.c. supply. Calculate
(a) the circuit time constant, (b) the initial charging current, (c) the p.d.s across the capacitor and
resistor 4 seconds after the supply is connected. You may assume that the capacitor is initially fully
discharged.
A
C 8 10
6
F; R 0.5 10
6
; E 200 V
200 V
0.5 MΩ
8 μF
Fig. 8.8
(a)
CR second
so s
80 050
4
66
11.
Ans
(b)
I
I
0
6
0
200
05 0
400
E
R
amp
therefore A
. 1
μ Ans
(c)
After seconds, volt
V
vE
v
v
C
C
R
0 632 0 632 200
26 4
..
.1 Ans
EEv
v
C
R
volt
so V
200 26 4
73 6
1 .
. Ans
8.2 Capacitor-Resistor Series Circuit (Discharging)
Consider the circuit of Fig. 8.1 , where the switch has been in position
‘ B ’ for suffi cient time to allow the charging process to be completed.

254
Fundamental Electrical and Electronic Principles
Thus the charging current will be zero, the p.d. across the resistor will
be zero, the p.d. across the capacitor will be E volt, and it will have
stored a charge of Q coulomb.
At some time t 0, let the switch be moved back to position ‘ A ’ . The
capacitor will now be able to discharge through resistor R. The general
equation for the voltages in the circuit will still apply.
In other words Ev v
RC
but, at the instant the switch is moved to position ‘ A ’ , the source of
emf is removed. Applying this condition to the general equation above
yields:
0
0
0
0
vv v E v IR
IR E
RC C R
; where and
so
hence ampI
E
R
0
(8.3)
This means that the initial discharge current has the same value as
the initial charging current, but (as you would expect) it fl ows in the
opposite direction.
Since the capacitor is discharging, then its voltage will decay from
E volt to zero; its charge will decay from Q coulomb to zero; and the
discharge current will also decay from I
0
to zero. The circuit time
constant will be the same as before i.e. CR seconds.
The graphs for v
C
and i are shown in Fig. 8.9 .
5τ
t(s)
0
E
V
c
(V)
V
c
I
0
i
i
τ
Fig. 8.9

D.C. Transients
255
Note: The time constant for the C-R circuit was defi ned previously in
terms of the capacitor charging. However, a time constant also applies
to the discharge conditions. It is therefore better to defi ne the time
constant in a more general manner, as follows:
The time constant of a circuit is the time that it would have taken for
any transient variable to change, from one steady state to a new steady
state, if it had maintained its rate of change existing at the time of the
fi rst steady state.
Worked Example 8.2
Q A C-R charge/discharge circuit is shown in Fig. 8.10 . The switch has been in position ‘ 1 ’ for a su cient
time to allow the capacitor to become fully discharged.
(a) If the switch is now moved to position ‘ 2 ’ , calculate the time constant and initial charging current.
(b) After the capacitor has completely charged the switch is moved back to position ‘ 2 ’ . Calculate the
time constant and the p.d across R
2
at this time.
150 V
E
R
1
R
2
C
110 kΩ
220 kΩ
‘2’
‘1’
0.5 μF
Fig. 8.10
A
C 0.5 μ F ; R
1
220 k ; R
2
110 k ; E 150 V
(a) When charging, only resistor R
1
is connected in series with the capacitor,
so R
2
may be ignored.
CR
E
R
1
11
11
1
seconds
so s
amp
0 5 0 220 0
0
50
63
0
.
. Ans
I
2220 0
682
3
0
1
I μA Ans
(b) When discharging, both R
1
and R
2
are connected in series with the
capacitor, so their combined resistance R R
1
R
2
, will determine the
discharge time constant.
CR seconds
so, s
0 5 0 330 0
06
63
.
.
11
1 Ans
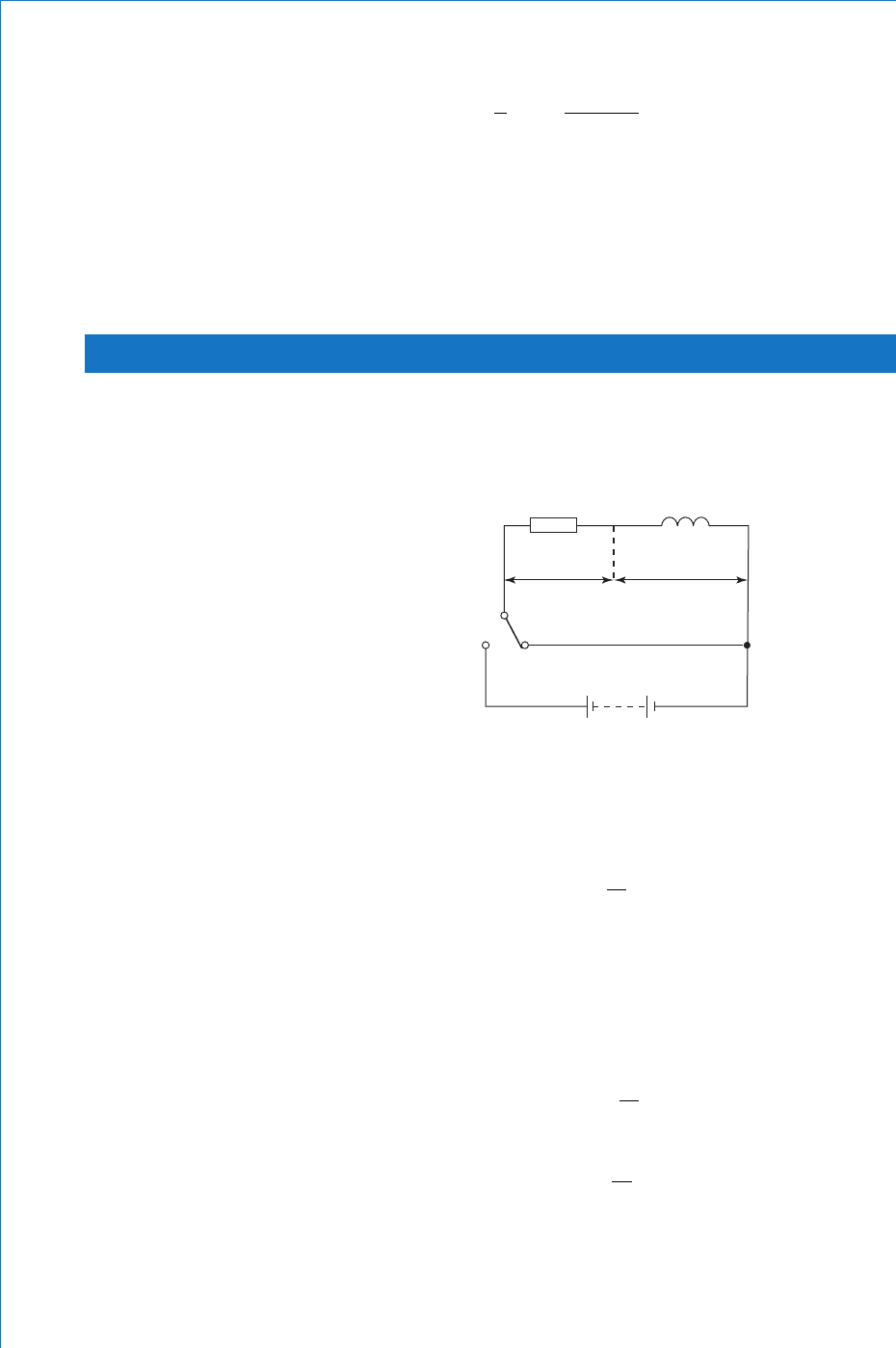
256
Fundamental Electrical and Electronic Principles
After one time constant the discharge current will have fallen to 0.368 I
0
I
I
0
3
0
6
2
50
330 0
454 5
0 368 454 0
67 26
E
R
i
i
v
R
amp
A
A
1
1
1
1
.
.
.
iR
v
R
2
63
2
67 26 0 0 0
84
volt
V
11111
1
.
. Ans
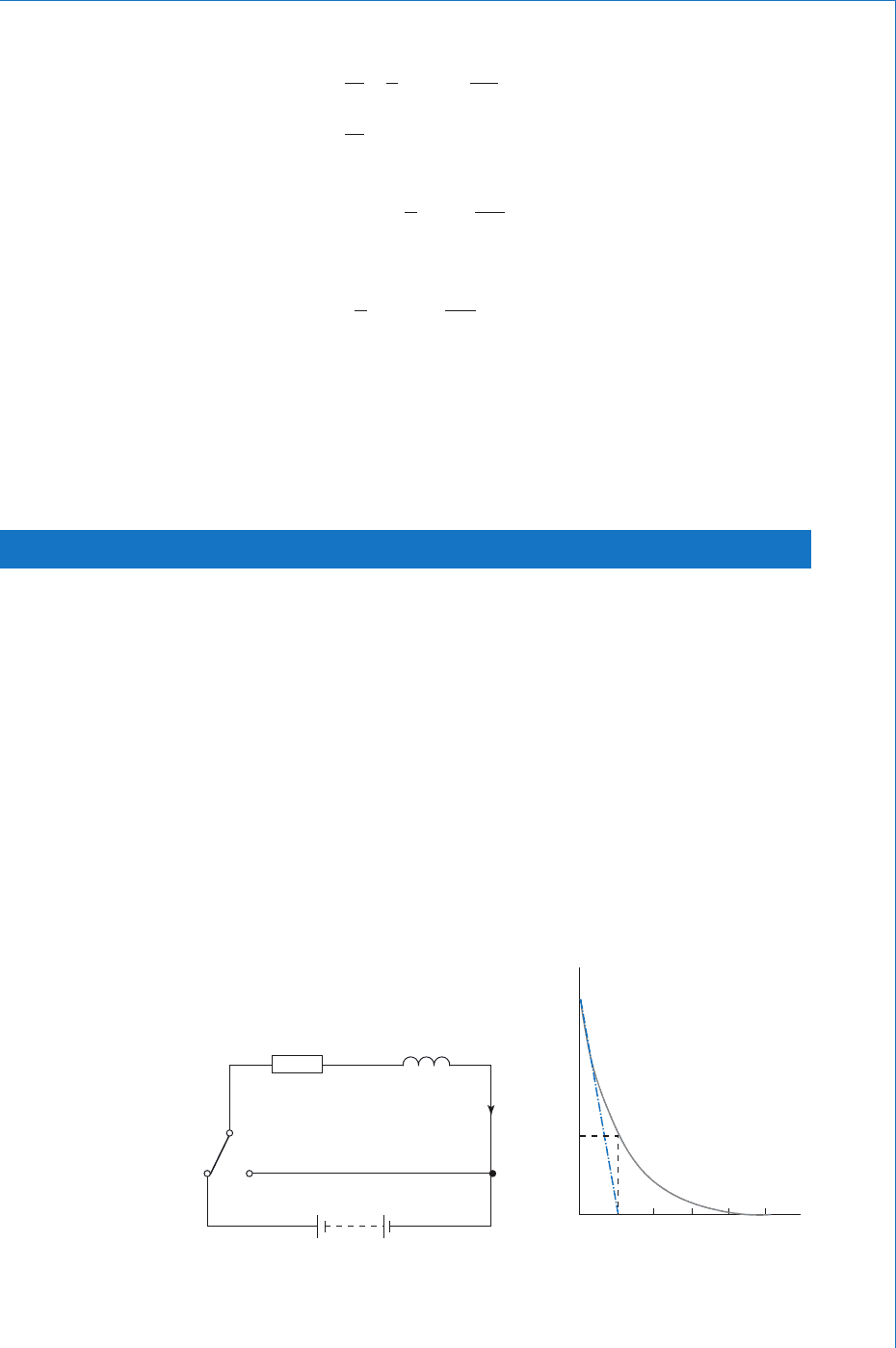
8.3 Inductor-Resistor Series Circuit (Connection to Supply)
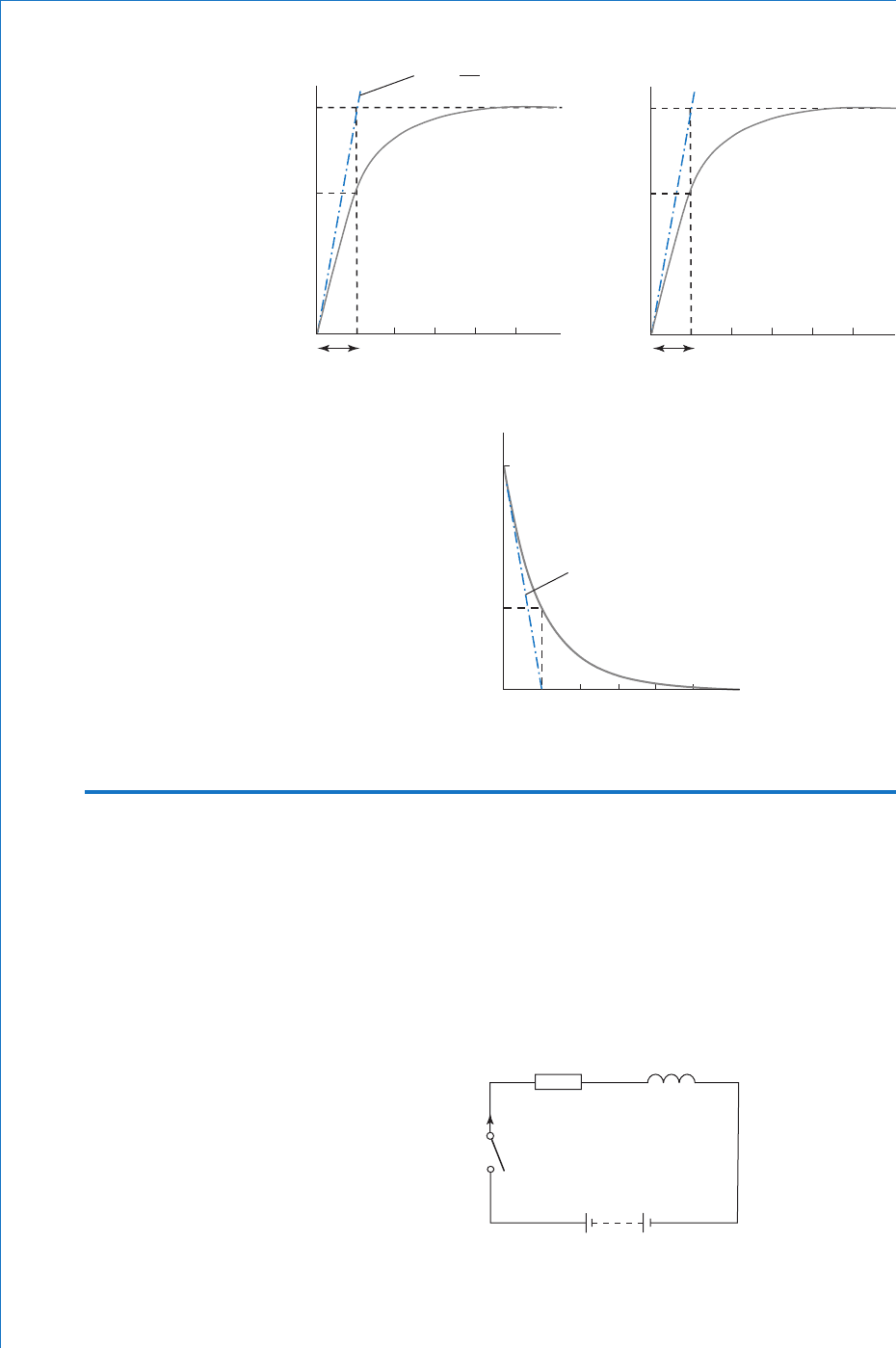
Consider the circuit of Fig. 8.11. At some time t 0, the switch is
moved from position ‘ A ’ to position ‘ B ’ . The connection to the supply is
now complete, and current will start to fl ow, increasing towards its fi nal
R
‘B’
‘A’
E
RL
i
V
R
V
L
Fig. 8.11
steady value. However, whilst the current is changing it will induce a
back-emf across the inductor, of e volt. From electromagnetic induction
theory we know that this induced emf will have a value given by:
eL
i
t
d
d
volt
Being a simple series circuit, Kirchhoff ’ s voltage law will apply, such
that the sum of the p.d.s equals the applied emf. Also, since we are
considering a perfect inductor (the resistor shown may be considered as
the coil ’ s resistance), the p.d. across the inductor will be exactly equal
but opposite in polarity to the induced emf.
Therefore,
d
d
volt
hence, volt
or,
d
d
veL
i
t
Ev v
EiRL
i
L
RL
tt
volt...............[ ]1
Comparing this equation with that for the C-R circuit, it may be seen
that they are both of the same form. Using the analogy technique, we

D.C. Transients
257
can conclude that both systems will respond in a similar manner. In the
case of the L-R circuit, the current will increase from zero to its fi nal
steady value, following an exponential law.
At the instant that the switch is moved from ‘ A ’ to ‘ B ’ ( t 0), the
current will have an instantaneous value of zero, but it will have a
certain rate of change, d i /d t amp/s. From eqn [1] above, this initial rate
of change can be obtained, thus:
EL
i
t
0
d
d
so, initial
d
d
amp/s
i
t
E
L
(8.4)
When the current reaches its fi nal steady value, there will be no back-
emf across the inductor, and hence no p.d. across it. Thus the only
limiting factor on the current will then be the resistance of the circuit.
The fi nal steady current is therefore given by:
I
E
R
amp
(8.5)
The time constant of the circuit is obtained by dividing the inductance
by the resistance.
Thus seconds
L
R
(8.6)
The above equation may be confi rmed by using a simple form of
dimensional analysis, as follows.
In general, ; so
and
therefore,
V
LI
t
L
Vt
I
R
V
I
L
R
Vt
I
I
V
t
seconds
The time constant of the circuit may be defi ned in the general terms
given in the ‘Note ’ , in the previous section, dealing with the C-R
circuit.
The rate of change of current will be at its maximum value at time t 0,
so the p.d. across the inductor will be at its maximum value at this time.
This p.d. therefore decays exponentially from E volt to zero. The graphs
for i, v
R
, and v
L
are shown in Figs. 8.12 to 8.14 respectively.
258
Fundamental Electrical and Electronic Principles
Worked Example 8.3
Q T h e eld winding of a 110 V, d.c. motor has an inductance of 1.5 H, and a resistance of 220 . From
the instant that the machine is connected to a 110 V supply, calculate (a) the initial rate of change
of current, (b) the nal steady current, and (c) the time taken for the current to reach its nal steady
value.
A
E 110 V ; L 1.5 H; R 220
The circuit diagram is shown in Fig. 8.15 .
τ 2τ 3τ 4τ 5τ
t(s)0
0.368 E
E
V
L
(V)
initial rate of change
Fig. 8.14
0.632 I
I
i (A)
initial
di
dt
τ
0
2τ 3τ 4τ 5τ
t(s)
Fig. 8.12
τ
0
0.632 E
E
V
R
(V)
2τ 3τ 4τ 5τ
t(s)
Fig. 8.13
E
110 V
220 Ω
1.5 H
i
Fig. 8.15
D.C. Transients
259
(a)
initial
d
d
amp/s
so, initial
d
d
A/s
i
t
E
L
i
t
11
1
0
5
73 33
.
. Ans
(b)
final current, amp
therefore, A
I
I
E
R
110
220
05. Ans
(c)
L
R
second
hence, ms
1.
.
5
220
682
Since the system takes approximately 5 seconds to reach its new steady state,
then the current will reach its nal steady value in a time:
t 5 6 82 34..ms ms 1 Ans
8.4 Inductor-Resistor Series Circuit (Disconnection)
Figure 8.16 shows such a circuit, connected to a d.c. supply. Assume
that the current has reached its fi nal steady value of I amps. Let the
switch now be returned to position ‘ A ’ (at time t 0). The current will
now decay to zero in an exponential manner. However, the decaying
current will induce a back-emf across the coil. This emf must oppose
the change of current. Therefore, the decaying current will fl ow in
the same direction as the original steady current. In other words, the
back-emf will try to maintain the original current fl ow. The graph of
the decaying current, with respect to time, will therefore be as shown
in Fig. 8.17. The time constant of the circuit will, of course, still be L / R
second, and the current will decay from a value of I E / R amp. The
initial rate of decay will also be E / L amp/s.
τ 2τ 3τ 4τ 5τ
t(s)0
0.368 I
i (A)
I
Fig. 8.17
‘B’
‘A’
R
E
L
i
Fig. 8.16

260
Fundamental Electrical and Electronic Principles
Summary of Equations
C-R circuit:
Time constant, CR second
Initial current,
I
E
R
0
amp
steady-state conditions after approx. 5 second
after, second, v
C
0.632E volt; and i 0.368I
0
amp
L-R circuit:
Time constant, second
Initial rate of change of current
L
R
,,
d
d
amp/second
final current flowing, amp
i
t
E
L
I
E
R
steady-state conditions after approx. 5 second
after second, V
L
0.368 E volt; and i 0.632 I amp
