Robertson C.R. Fundamental electrical and electronic principles
Подождите немного. Документ загружается.

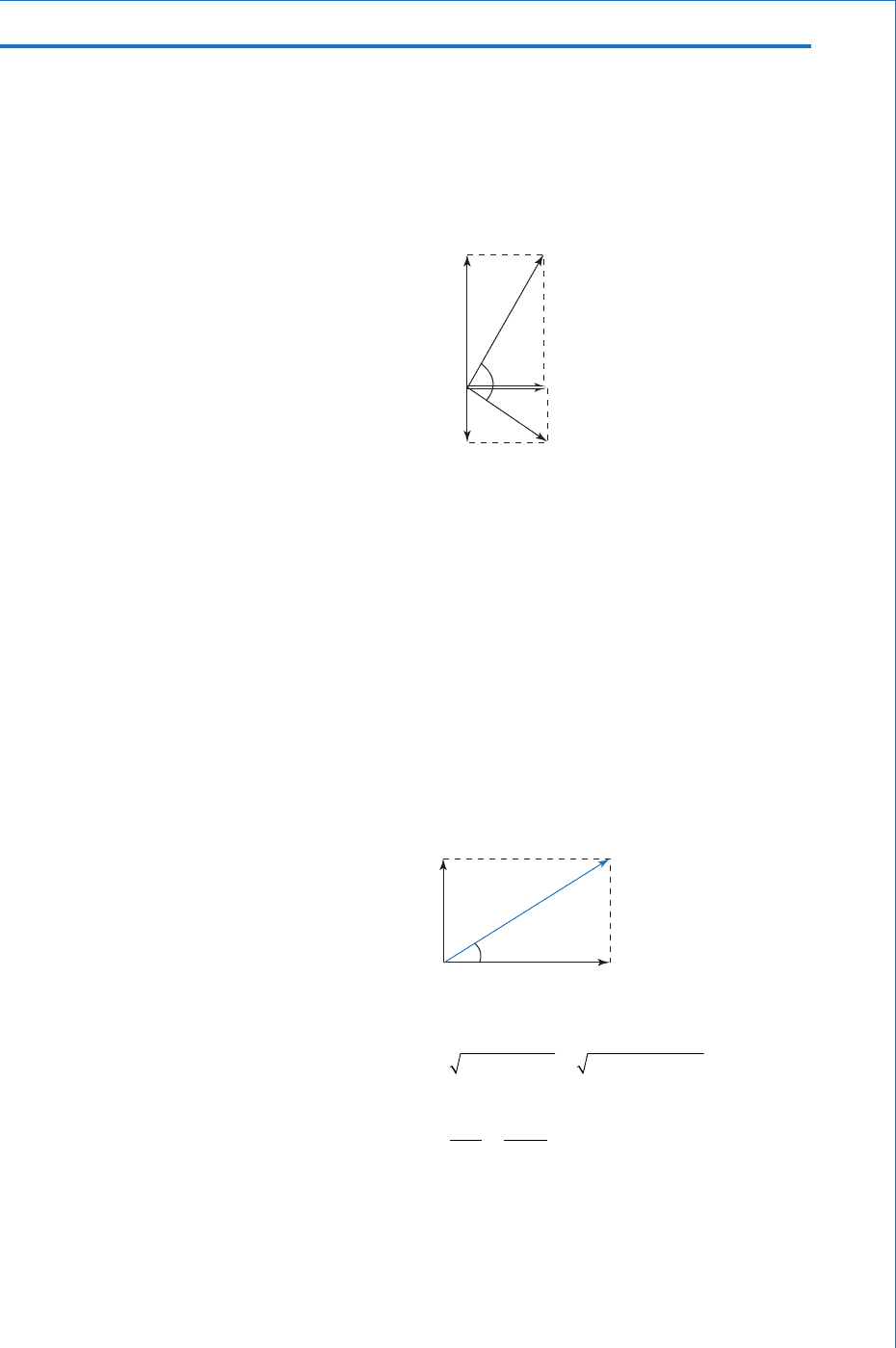
Alternating Quantities
221
Worked Example 6.13
Q Determine the phasor sum of the two voltages speci ed below.
v
1
25 sin (314 t /3), and v
2
15 sin (314 t /6) volt
A
Figure 6.27 shows the sketch of the phasor diagram.
/3
/6
25 V
15 V
Fig. 6.27
Note: Always sketch a phasor diagram.
H.C. cos / cos /
()( )
25 3 5 6
25 0 5 5 0 866
25 29
1
1
11
()
..
..99
25 49so, H.C. V .
V.C. sin / sin /
()( )
25 3 5 6
25 0 866 5 0 5
265 7
1
1
1
()
.(.)
...
.
5
45so, V.C. V11
Figure 6.28 shows the phasor diagram for H.C., V.C. and V
m
.
H.C.
V. C.
V
m
Fig. 6.28
V
V
m
m
H.C. V.C.
so, V
tan
V.C.
H.C.
22 2 2
25 49 4 5
29 5
4
..
.
11
1
1
φ
..
.
.
..
1
1
5
25 49
0 555
0 555 0 507
29
*
so, tan rad
therefore,
φ
v .. .115 3 4 0 507 sin( ) volt t Ans
*radian mode required
222
Fundamental Electrical and Electronic Principles
Worked Example 6.14
Q Calculate the phasor sum of the three currents listed below.
it
it
it
1
6
82
46
2
3
sin amp
sin( / ) amp
sin( / ) amp
ω
ωπ
ωπ
A
The relevant phasor diagrams are shown in Figs. 6.29 and 6.30.
4A
6A
8A
/6
Fig. 6.29
H.C.
V. C.
I
m
Fig. 6.30
H.C. cos cos / cos /
()(8)( )
608 24 6
6 0 4 0 866
6
()
.
ππ
1
346
946
608 24 6
.
.
()
so, H.C. A
V.C. sin sin / sin /ππ
(()( )( )
so, V.C. A
H.C. V.C.
60 8 405
82
6
9
22
[] .
.
1
I
m
446 6
2
6
946
0
22
()
so, A
tan
V.C.
H.C.
tan tan
I
m
11
11 1
.
.
φ ..
.
..
6342
0 565
2 0 565
so, rad
therefore, sin( ) amp
φ
ω
it11 Anns
Worked Example 6.15
Q Three alternating voltages and one current are as speci ed in the expressions below.
v
1
10 sin(628t /6) volt
v
2
8 sin(628t /3) volt
v
3
12 sin(628t /4) volt
i 6 sin(628t) amp
(a) For each voltage determine the frequency, phase angle and amplitude.
(b) Determine the phasor sum of the three voltages.

Alternating Quantities
223
A
(a) All four waveforms have the same value of 628 rad/s, so they are all of
the same frequency, hence
2 628
628
2
00
f
f
f
so, Hz
and, Hz 1 Ans
for , / rad or ; and V
for , /
vV
v
m11
1φ
φ
630 0
3
22
Ans
rrad or ; and V
for , / rad or ; and
60 8
445
33
V
v
m
Ans
φ VV
m
12V Ans
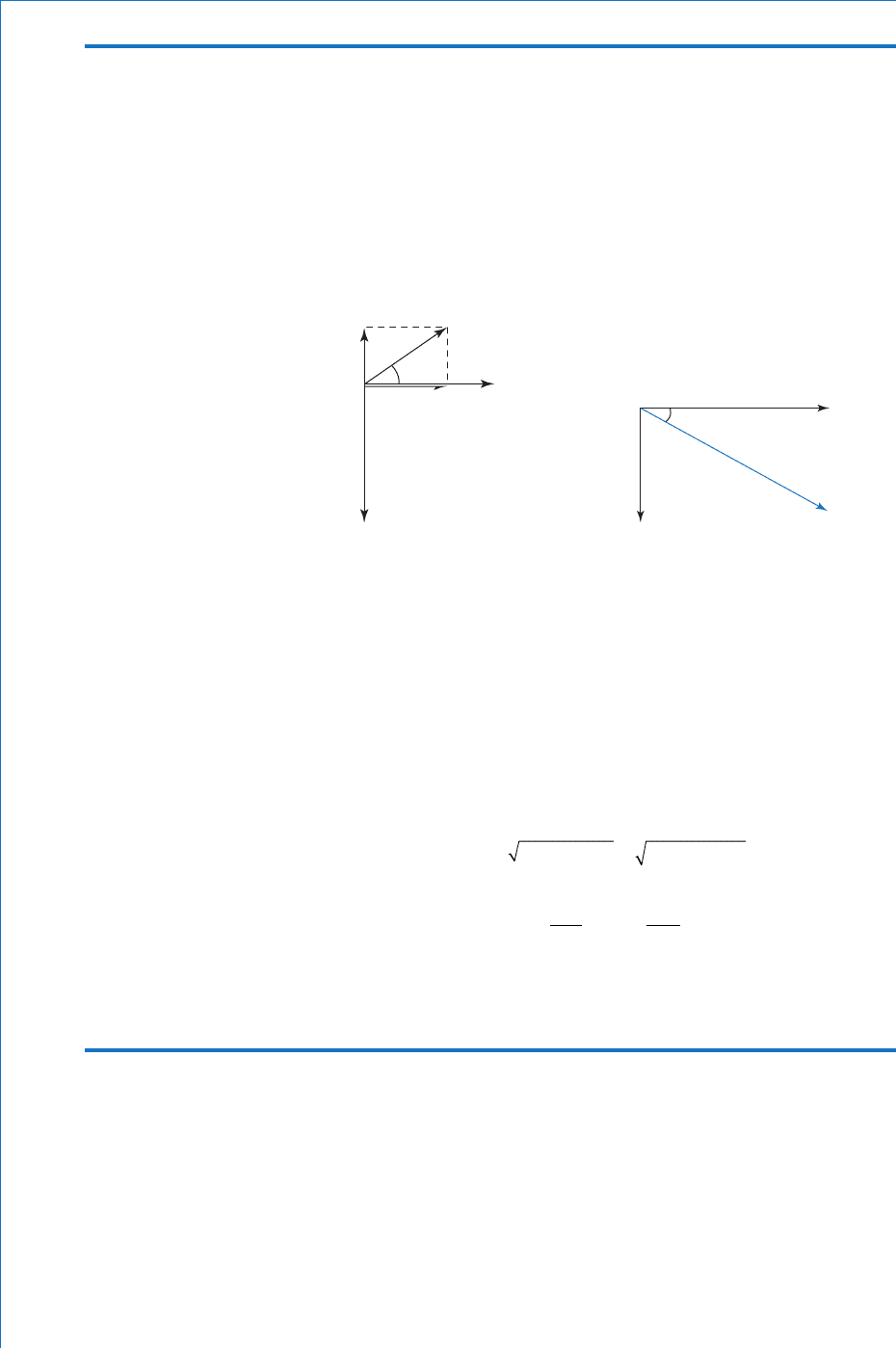
(b) Firstly the phasor diagram ( Fig. 6.31 ) is sketched, very roughly to scale. In
order to do this a reference waveform needs to be selected, and since the
current has a zero phase angle, this is chosen as the reference. However, if the
current waveform had not been speci ed, the horizontal axis would still be
taken as the reference from which all phase angles are measured. Since v
2
and
v
3
have positive phase angles, and phasors rotate anticlockwise, then these
two phasors will appear above the reference axis. The voltage v
1
, having a
negative phase angle will appear below the reference axis. Also shown on the
phasor diagram are the horizontal and vertical components of each voltage.
I
m
(ref)
10 V
12 V
8 V
/3
/4
/6
Fig. 6.31
H.C. 2 cos / cos / cos /
()()(
11
11
48 3 0 6
2 0 707 8 0 5 0 0 8...666
8484866
244
24830
)
so, H.C. V
V.C. sin / sin / sin
..
.1
11 /
()()()
and V.C.
6
2 0 707 8 0 866 0 0 5
8 48 6 928 5
0
11
1
.. .
..
.. 4 21 V
The phasor diagram for H.C. and V.C., and the resultant phasor sum is Fig. 6.32 .
224
Fundamental Electrical and Electronic Principles
V
V
m
m
H.C. V.C.
so, V
tan
V.C.
H.C.
22 2 2
244 042
23 83
111
1
..
.
φ
ttan tan
and, rad
11
11
1
04 2
244
0 4856
0 452
.
.
.
.φ
Hence, the phasor sum, v 23.83 sin (628 t 0.452) volt Ans
6.15 The Cathode Ray Oscilloscope
The name of this instrument is more often abbreviated to the oscilloscope,
the ‘ scope, or CRO. It is a very versatile instrument, that may be used to
measure both a.c. and d.c. voltages. For d.c. measurements, a voltmeter
is usually more convenient to use. The principal advantages of the
oscilloscope when used to measure a.c. quantities are:
1 A visual indication of the waveform is produced.
2 The frequency, period and phase angle of the waveform(s) can be
determined.
3 It can be used to measure very high frequency waveforms.
4 Any waveshape can be displayed, and measured with equal accuracy.
5 The input resistance (impedance) is of the same order as a digital
voltmeter. It therefore applies minimal loading effect to a circuit to
which it is connected.
6 Some oscilloscopes can display two or more waveforms
simultaneously.
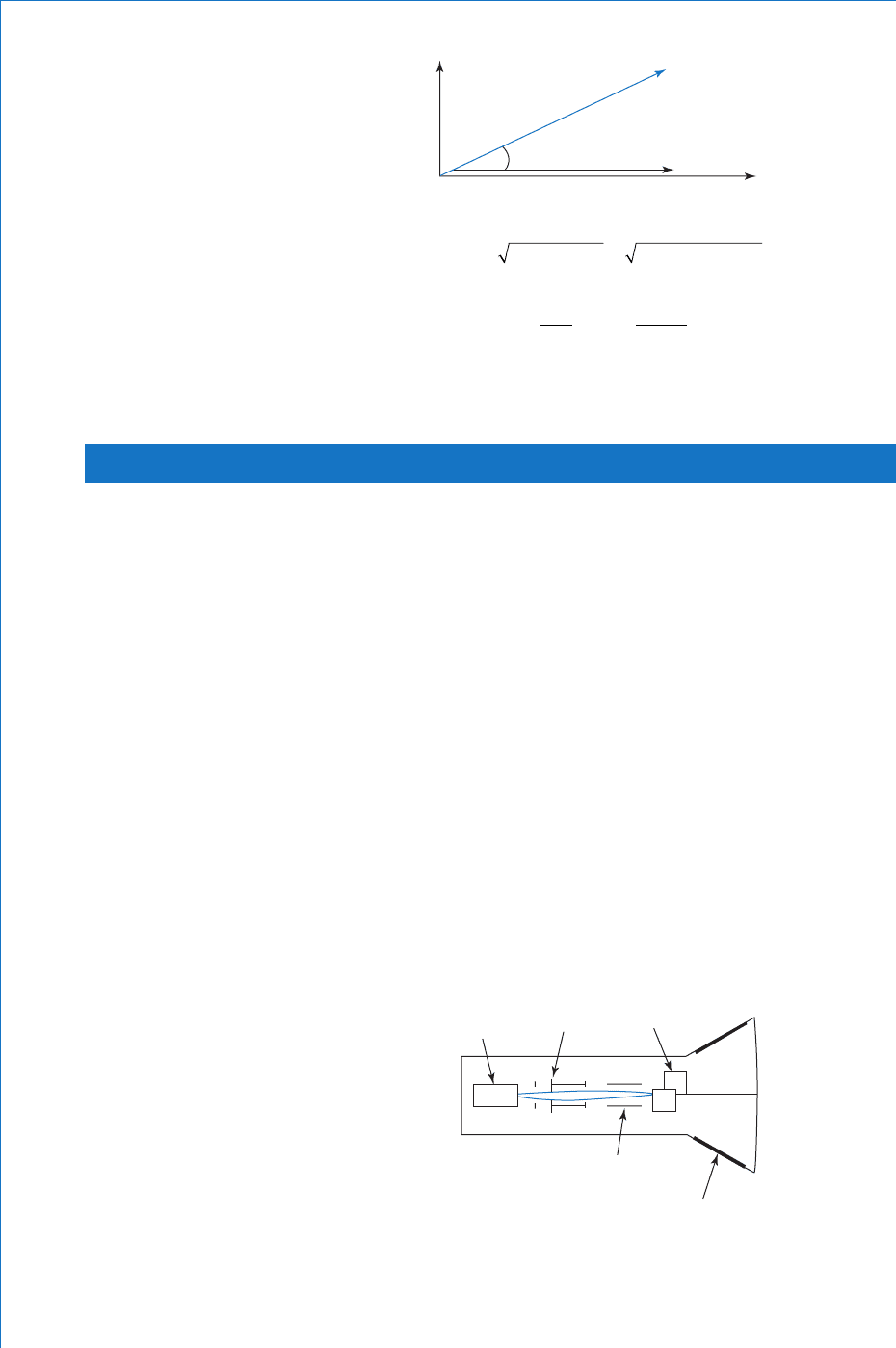
Cathode Ray Tube The basic arrangement of a crt is shown in
Fig. 6.33 . The main components are contained within an evacuated
H.C.
V
m
I
m
(ref)
V. C .
Fig. 6.32
X
deflection
anodes
electron
gun
Y deflection
graphite
coating
Fig. 6.33

Alternating Quantities
225
glass tube. These components are: the electron gun; a focusing system;
a beam defl ection system; and a screen. Each of these will be very
briefl y described.
Electron gun assembly This component produces a beam of
electrons. This beam can then be accelerated, down the axis of the
tube, by a series of high potential anodes.
Focusing system The beam consists entirely of electrons. Since
they are all negatively charged, then they will tend to repel each other.
The beam will therefore tend to spread out, and this would result in a
very fuzzy display. The focusing system consists of a series of high
potential anodes. These also provide the acceleration for the electron
beam. Each successive anode along the tube, towards the screen, is at
a higher potential than the previous one. The electric fi elds, between
these anodes, will be of the same shape as a double convex optical lens.
This is referred to as an electron lens, and causes the beam to converge
to a small spot by the time it reaches the screen.
Defl ection system Two sets of parallel plates are situated after the
last anode. One set is mounted in the horizontal, and the other set in the
vertical plane. These are the X-plates and the Y-plates. When a p.d. is
developed between a pair of plates, an electric fi eld will exist between
them. This electric fi eld will cause the electrons in the beam to be
defl ected, towards the more positive of the two plates. Thus, the beam can
be made to defl ect in both planes. This effect is illustrated in Fig. 6.34 .
Fig. 6.34
The screen The inner surface of the screen is coated with a phosphor.
Wherever the electron beam strikes the phosphor, it will glow very
briefl y. This is because the kinetic energy of the bombarding electrons
is converted into ‘ light ’ energy. On the inside of the ‘ bell ’ shape of the
tube is a graphite coating. This provides a conducting path to return the
electrons to the internal power supply, and hence complete the circuit
back to the electron gun.
In order for a waveform to be displayed on the screen, the beam must
be swept at a constant speed across the screen. At the same time, the
beam has to be defl ected up and down. You can demonstrate this for
226
Fundamental Electrical and Electronic Principles
yourself, as follows. Take a pencil and a sheet of paper. At the left-
hand edge of the paper, move the pencil up and down, at as constant
a rate as possible. Maintaining this up-and-down rhythm, now move
the pencil across the page, again at as constant a rate as possible. The
pattern traced on to the paper should now resemble a sinewave.
The electron beam in the crt is subjected to similar forces, exerted by
the defl ecting plates, when displaying a sinusoidal waveform. The
X-plates cause the beam to be swept across the screen at a constant
rate. The Y-plates cause the beam to defl ect up and down, in sympathy
with the voltage being displayed.
6.16 Operation of the Oscilloscope
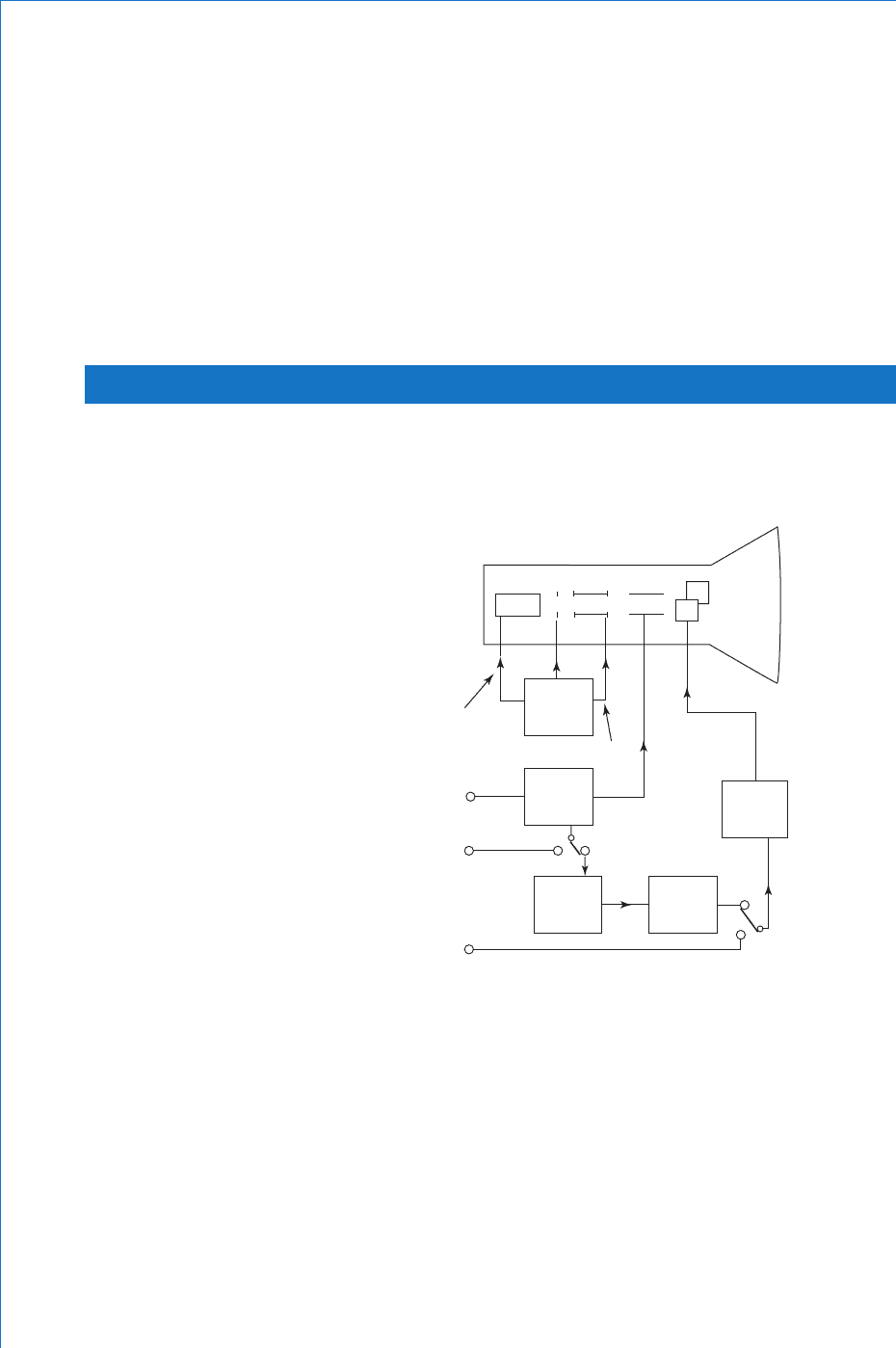
In addition to the crt, the other main components in the oscilloscope enable
the user to adjust the display, by means of controls on the front panel.
A simplifi ed block diagram of the oscilloscope is shown in Fig. 6.35 .
brightness
Power
supply
focus
Y-amp.
Trigger
pulse
gen.
Time-
base
gen.
X-amp
Y
input
X
input
Ext.
trig.
Fig. 6.35
The Power Supply This provides the high potentials required for the
anodes. It also provides the d.c. supplies for the amplifi ers, the electron
gun, the timebase and trigger pulse generators.
The Focus Control This control allows the potentials applied to the
anodes to be varied. This allows the shape of the electron lens to be
altered, and hence achieve a sharp clear trace on the screen.
The Brightness Control This varies the potentials applied to the
electron gun. The number of electrons forming the beam are thus
controlled, which determines the brightness of the display.
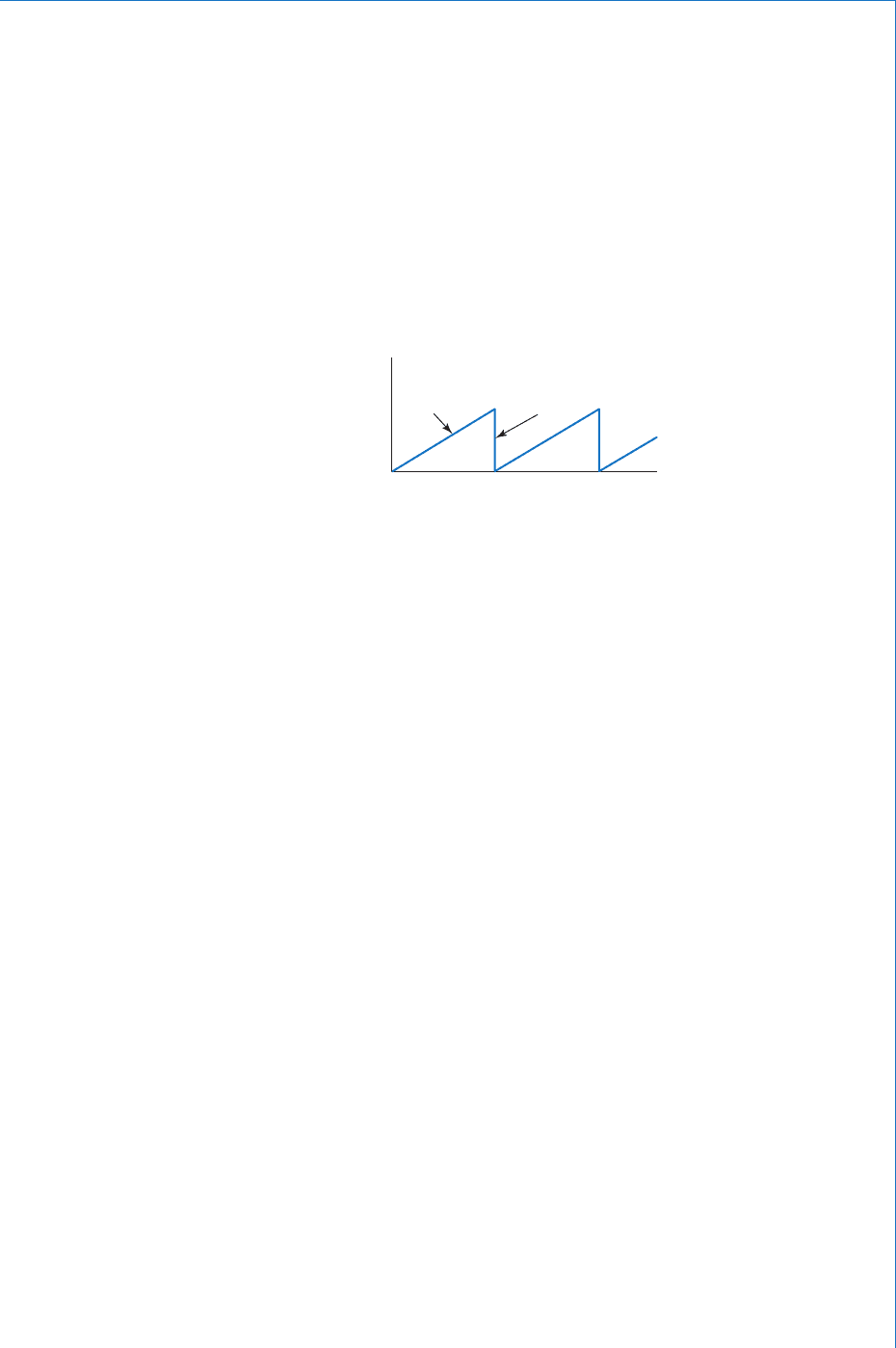
Alternating Quantities
227
The Timebase Control This controls the speed at which the beam is
swept across the screen, from left to right. It does this by setting the
‘ sweep ’ time of the Timebase generator.
This generator produces a sawtooth voltage, as illustrated in Fig. 6.36 .
This waveform is applied to the X-plates. During the sweep time,
the beam is steadily defl ected across the screen. During the ‘ fl yback ’
time, the beam is rapidly returned to the left-hand side of the screen,
ready for the next sweep. The steepness of the sweep section of this
waveform determines the speed of the sweep.
sweep flyback
t
V
Fig. 6.36
At the front of the screen is a graticule, marked out in centimetre
squares. The timebase control is marked in units of time/cm. Thus, if
this control is set to (say) 10 ms/cm, then each centimetre graduation
across the graticule represents a time interval of 10 ms. This facility
enables the measurement of the periodic time (and hence frequency),
of the displayed waveform.
Trigger Control This enables the user to obtain a single stationary
image of the trace on the screen. If this control is incorrectly set, then
the trace will scroll continuously across the screen. Alternatively,
multiple overlapping traces are displayed, which may also be scrolling.
In either case, measurement of the periodic time is impossible. This
control determines the point in time at which the sweep cycle of the
sawtooth waveform commences. If required an external trigger input
may be used.
X-Amplifi er This amplifi es the sawtooth waveform. This ensures that
the voltage applied to the X-plates is suffi ciently large to defl ect the
beam across the full width of the screen. There is also provision for the
application of an external timebase signal.
Y-Amplifi er The waveform to be displayed is applied to this
amplifi er. Thus, small amplitude signals can be amplifi ed to give
a convenient height of the trace. The gain or amplifi cation of this
amplifi er is determined by the user. The control on the front panel
is marked in units of volt/cm. Thus, if this control was set to (say)
100 mV/cm, then each vertical graduation on the screen graticule
represents a voltage of 100 mV. This enables the measurement of the
amplitude of the displayed waveform.
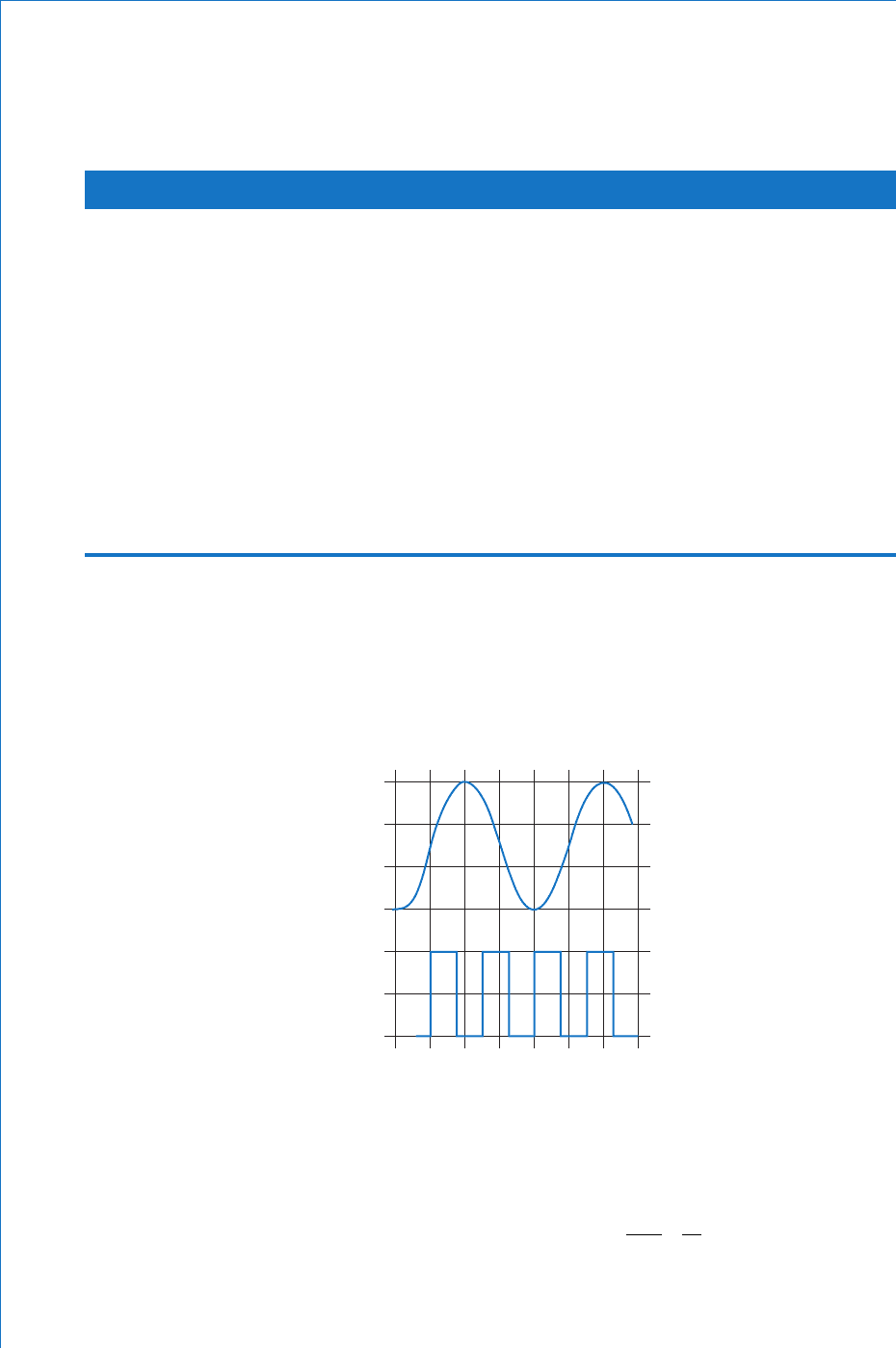
228
Fundamental Electrical and Electronic Principles
X and Y Shift Controls These controls enable the trace position on
the screen to be adjusted. This makes the measurement of period and
amplitude easier.
6.17 Dual Beam Oscilloscopes
These instruments are widely used, and are more versatile than the single
beam type described. They have the advantage that two waveforms can
be displayed simultaneously. This enables waveforms to be compared, in
terms of their amplitudes, shape, phase angle or frequency.
The principles of operation are exactly the same as for the single beam
instrument. They contain two electron gun assemblies, which have
common brightness and focusing controls. The timebase generator
is also common to both channels. There will be two separate
Y-amplifi ers, each controlling its own set of vertical defl ection
plates. The inputs to these two amplifi ers are usually marked as
channel 1 and channel 2, or as channels A and B.
Worked Example 6.16
Q The traces obtained on a double beam oscilloscope are shown in Fig. 6.37 . The graticule is marked in
1 cm squares. The channel 1 input is displayed by the upper trace. If settings of the controls for the
two channels are as follows, determine the amplitude, r.m.s. value, and frequency of each input.
Channel 1: timebase of 0.1 ms/cm; Y-amp setting of 5 V/cm
Channel 2: timebase of 10 μ s/cm; Y-amp setting of 0.5 V/cm
Fig. 6.37
A
Channel 1: peak to peak occupies 3 cm, so
V
V
V
pp
pp
m
35 5
2
5
2
75
1
1
V
the amplitude
therefore, V . Ans

Alternating Quantities
229
As the waveform is a sinewave, then r.m.s. value V V
m
I
2
therefore, V V
75
2
53
.
. Ans
1 cycle occupies 4 cm, so T 4 0.1 0.4 ms
f
T
f
11
1
Hz
so, kHz
04 0
25
3
.
. Ans
Channel 2: peak to peak occupies 2 cm, so
VV
pp m
205 05..1 V, and V Ans
Since it is a squarewave, then r.m.s. value amplitude,
hence V V 05. Ans
2 cycles occur in 3 cm, so 1 cycle occurs in 2/3 cm
therefore, T 0.6667 10 6.667 μ s
f
T
f
11
1
Hz
so, kHz
6 667 10
50
6
.
Ans
Summary of Equations
Frequency generated: f np hertz
Periodic time:
T
f
1
second
Angular velocity: 2 f rad/second
Standard expression for a sinewave:
e EEt
Eft
mm
m
sin( ) sin( )
sin( ) volt
φφ
φ2
Average value for a sinewave:
I
I
I
ave
m
m
2
0637
.
R.m.s. value for a sinewave:
I
I
I
m
m
2
0 707.
Peak factor for a sinewave:
max. value
r.m.s. value
1 414.
Form factor for a sinewave:
r.m.s.value
ave value
111.
230 Fundamental Electrical and Electronic Principles
Assignment Questions
1
A coil is rotated between a pair of poles.
Calculate the frequency of the generated
emf if the rotational speed is (a) 150 rev/s,
(b) 900 rev/minute, (c) 200 rad/s.
2 An alternator has 8 poles. If the motor winding
is rotated at 1500 rev/minute, determine
(a) the frequency of the generated emf, and
(b) the speed of rotation required to produce
frequency of 50 Hz.
3 A frequency of 240 Hz is to be generated by
a coil, rotating at 1200 rev/min. Calculate the
number of poles required.
4 A sinewave is shown in Fig. 6.38 . Determine its
amplitude, periodic time and frequency.
5 A sinusoidal current has a peak-to-peak value
of 15 mA and a frequency of 100 Hz. (a) Plot
this waveform, to a base of time, and (b)
write down the standard expression for the
waveform.
6 A sinusoidal voltage is generated by an 85
turn coil, of dimensions 20 cm by 16 cm. The
coil is rotated at 3000 rev/min, with its longer
sides parallel to the faces of a pair of poles. If
the ux density produced by the poles is 0.5 T,
calculate (a) the amplitude of the generated
emf, (b) the frequency, (c) the r.m.s. and
average values.
7 Write down the standard expression for a
voltage, of r.m.s. value 45 V, and frequency
1.5 kHz. Hence, calculate the instantaneous
value, 38 s after the waveform passes
through its zero value.
8 For each of the following alternating
quantities, determine (a) the amplitude and
r.m.s. value, and (b) the frequency and period.
(i) e 250 sin 50t volt
(ii) i 75 sin 628.3t milliamp
(iii) f 20 sin 100t milliweber
(iv) v 6.8 sin (9424.8tf) volt.
9 For a current of r.m.s. value 5 A, and frequency
2 kHz, write down the standard expression.
Hence, calculate (a) the instantaneous value
15 0 μ s after it passes through zero, and (b) the
time taken for it to reach 4 A, after passing
through zero for the rst time.
10 Calculate the peak and average values for a
250 V sinusoidal supply.
11 A sinusoidal current has an average value of
3.8 mA. Calculate its r.m.s. and peak values.
12 An alternating voltage has an amplitude of
500 V, and an r.m.s. value of 350 V. Calculate
the peak factor.
13 A waveform has a form factor of 1.6, and an
average value of 10 V. Calculate its r.m.s.
value.
14 A moving coil voltmeter, calibrated for
sinewaves, is used to measure a voltage
waveform having a form factor of 1.25.
Determine the true r.m.s. value of this voltage,
if the meter indicates 25 V. Explain why the
meter does not indicate the true value.
15 Explain why only sinusoidal waveforms can be
represented by phasors.
16 Sketch the phasor diagram for the two
waveforms shown in Fig. 6.39 .
17 Sketch the phasor diagram for the two
voltages represented by the following
expressions:
vt
vt
1
11
1
234
834 3
2
sin volt,
sin( / ) volt.
25
0
I (mA)
5
5
50
t(s)
Fig. 6.38
0
I (mA)
5
3
2
t
(rad)
Fig. 6.39
