Robertson C.R. Fundamental electrical and electronic principles

Подождите немного. Документ загружается.

D.C. Machines

241

shown in Fig. 7.12 , and from this it may be seen that the armature has

to supply current to both the load and the ﬁ eld, such that:

III

aLf

amp

(7.2)

Fig. 7.12

This self-excitation process can take place only if there is some

residual ﬂ ux in the poles, and if the resistance of the ﬁ eld circuit is

less than some critical value. The open-circuit characteristic is

illustrated in Fig. 7.13 .

Fig. 7.13

The resistance of the ﬁ eld winding, R

, is constant and of a relatively

high value compared with R

. Typically, I

will be in the order of 1A

to 10A, and will remain reasonably constant. The shunt machine is

therefore considered to be a constant-ﬂ ux machine. When switch

S is closed, the armature current will increase in order to supply the

demanded load current, I

. Thus I

 I

, and as the load current is

increased, so the terminal voltage will fall, according to the equation,

V  E  I

volt. The output characteristic will therefore follow

much the same shape as that for the separately excited generator and

is shown in Fig. 7.14 . This condition applies until the machine is

providing its rated full-load output. If the load should now demand

even more current, i.e. the machine is overloaded, the result is that the

generator simply stops generating. This effect is shown by the dotted

lines in the output characteristics.

242

Fundamental Electrical and Electronic Principles

The shunt generator is the most commonly used d.c. generator, since it

provides a reasonably constant output voltage over its normal operating

range. Its other obvious advantage is the fact that it is self-exciting,

and therefore requires only some mechanical means of driving the

armature.

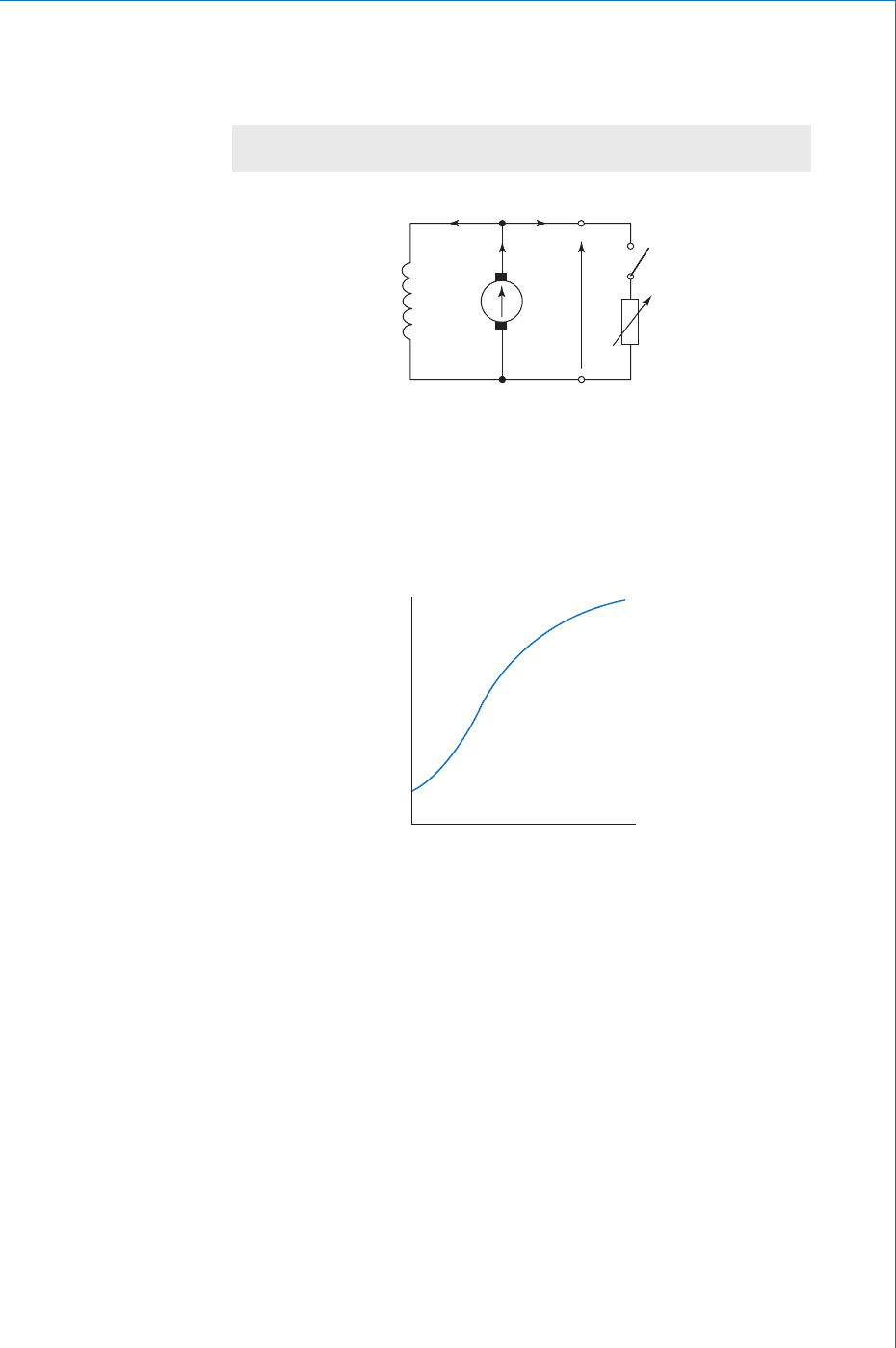
7.7 Series Generator

In this machine the ﬁ eld winding is connected in series with the

armature winding and the load, as shown in Fig. 7.15 . In this case,

 I

, so this is a variable-ﬂ ux machine. Since the ﬁ eld winding

must be capable of carrying the full-load current (which could be

in hundreds of amps for a large machine), it is usually made from a

few turns of heavy gauge wire or even copper strip. This also has the

advantage of offering a very low resistance. This generator is a self-

excited machine, provided that it is connected to a load when started.

Note that a shunt generator will self-excite only when disconnected

from its load.

When the load on a series generator is increased, the ﬂ ux produced will

increase, in almost direct proportion. The generated emf will therefore

voltage

full-load

Fig. 7.14

 I

Fig. 7.15

D.C. Machines

243

increase with the demanded load. The increase of ﬂ ux, and hence

voltage, will continue until the onset of magnetic saturation, as shown

in the output characteristic of Fig. 7.16 . The terminal voltage is related

to the emf by the equation:

VEIR R

aa f

 ( )volt

(7.3)

The variation of terminal voltage with load is not normally a

requirement for a generator, so this form of machine is seldom used.

However, the rising voltage characteristic of a series-connected

ﬁ eld winding is put to good use in the compound machine, which is

described in Further Electrical and Electronic Principles .

200 Ω

450V

475V

Fig. 7.17

emf

0 I

 R

)

Fig. 7.16

Worked Example 7.1

Q The resistance of the  eld winding of a shunt generator is 200  . When the machine is delivering

80 kW the generated emf and terminal voltage are 475 V and 450 V respectively. Calculate (a) the

armature resistance, and (b) the value of generated emf when the output is 50 kW, the terminal

voltage then being 460 V.

 200  ; P

 80  10

watt; V  450 V; E  475 V

The circuit diagram is shown in Fig. 7.17 . It is always good practice to sketch the

appropriate circuit diagram when solving machine problems.

244

Fundamental Electrical and Electronic Principles

(a)

oL L









watt; so amp

therefore A

80 0

450

77 8

1 .

aLf

REV

amp A

volt



 

   

450

200

225

80 05

475 450

.III

225

80 05

0 139

therefore ohmR



1 .

.  Ans

(b)

When W, V

thus A

 









50 0 460

50 0

460

08 7

460

000

08 7 2 3

460 0 13





   

hence, A

volt (

EV R

1 111

111 99

475 4

)

therefore V E  . Ans

Note : Although the load had changed by about 60%, the  eld current has

changed by only about 2.2%. This justi es the statement that a shunt generator

is considered to be a constant- ux machine.

7.8 D.C. Motors

All of the d.c. generators so far described could be operated as motors,

provided that they were connected to an appropriate d.c. supply. When

the machine is used as a motor, the armature generated emf is referred

to as the back-emf, E

, which is directly proportional to the speed of

rotation. However, the speed is inversely proportional to the ﬁ eld ﬂ ux  .

In addition, the torque produced by the machine is proportional to both

the ﬂ ux and the armature current. Bearing these points in mind, we can

say that:

Speed, 





(7.4)

and torque, TI

  (7.5)

7.9 Shunt Motor

When the machine reaches its normal operating temperature, R

will

remain constant. Since the ﬁ eld winding is connected directly to a

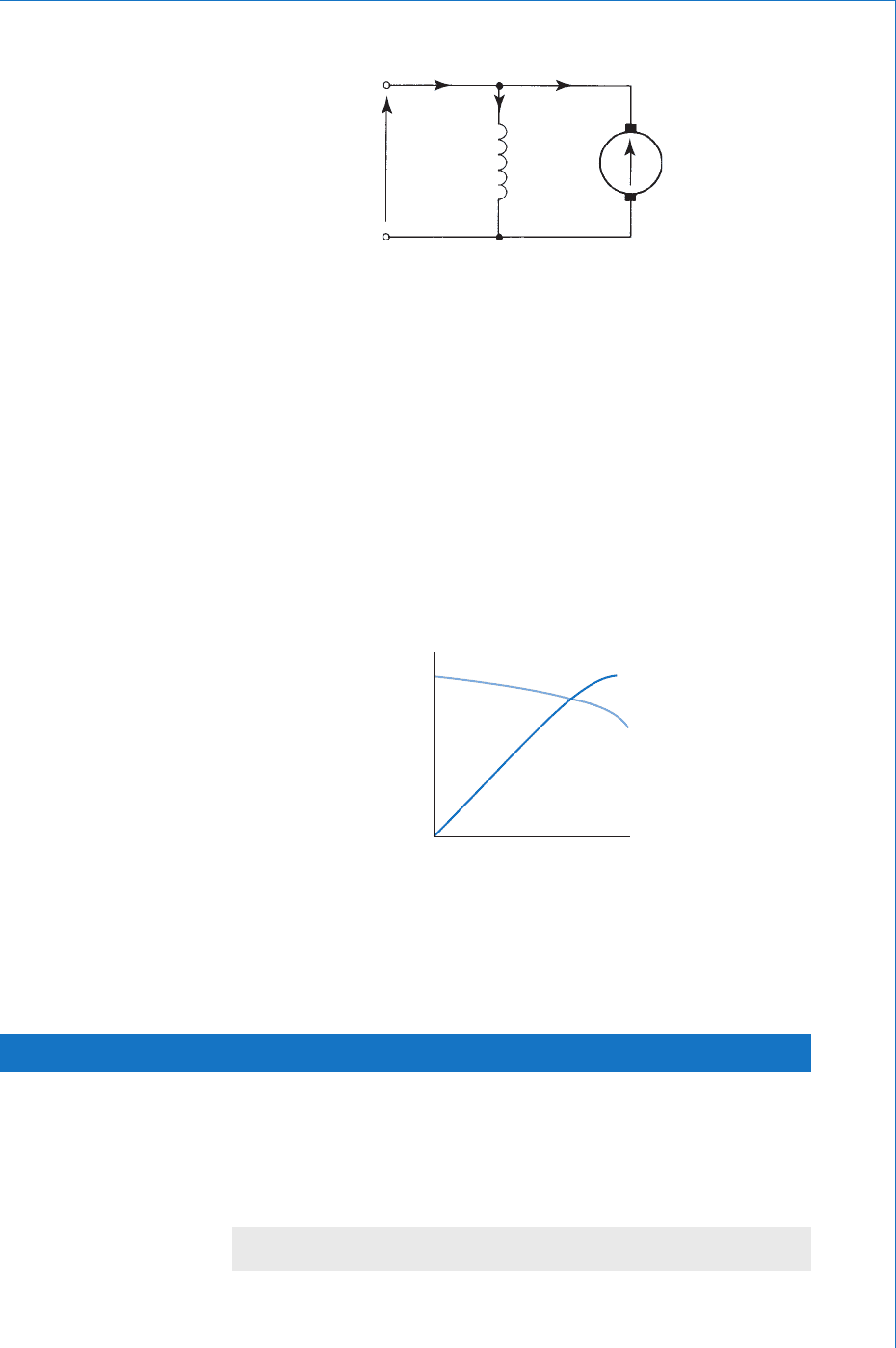
D.C. Machines

245

ﬁ xed supply voltage, V volt, then I

will be ﬁ xed. Thus, the shunt

motor ( Fig. 7.18 ) is a constant-ﬂ ux machine.

As the back-emf will have the same shape graph as that for the

generator emf, and using (7.4) and (7.5) the graphs of speed and torque

versus current will be as in Fig. 7.19 . Note that when the machine

is used as a motor, the supply current is identiﬁ ed as I

. In this case,

the subscript ‘ L ’ represents the word ‘ line ’ . Thus I

identiﬁ es the line

current drawn from the supply, and I

is directly proportional to I

Fig. 7.18

speed or

torque

0 I

Fig. 7.19

Shunt motors are used for applications where a reasonably constant

speed is required, between no-load and full-load conditions.

7.10 Series Motor

Like the series generator, this machine is a variable-ﬂ ux machine.

Despite this, the back-emf of this motor remains almost constant,

from light-load to full-load conditions. This fact is best illustrated by

considering the circuit diagram ( Fig. 7.20 ), with some typical values.

EVIRR

baaf

 ( ) volt

(7.6)

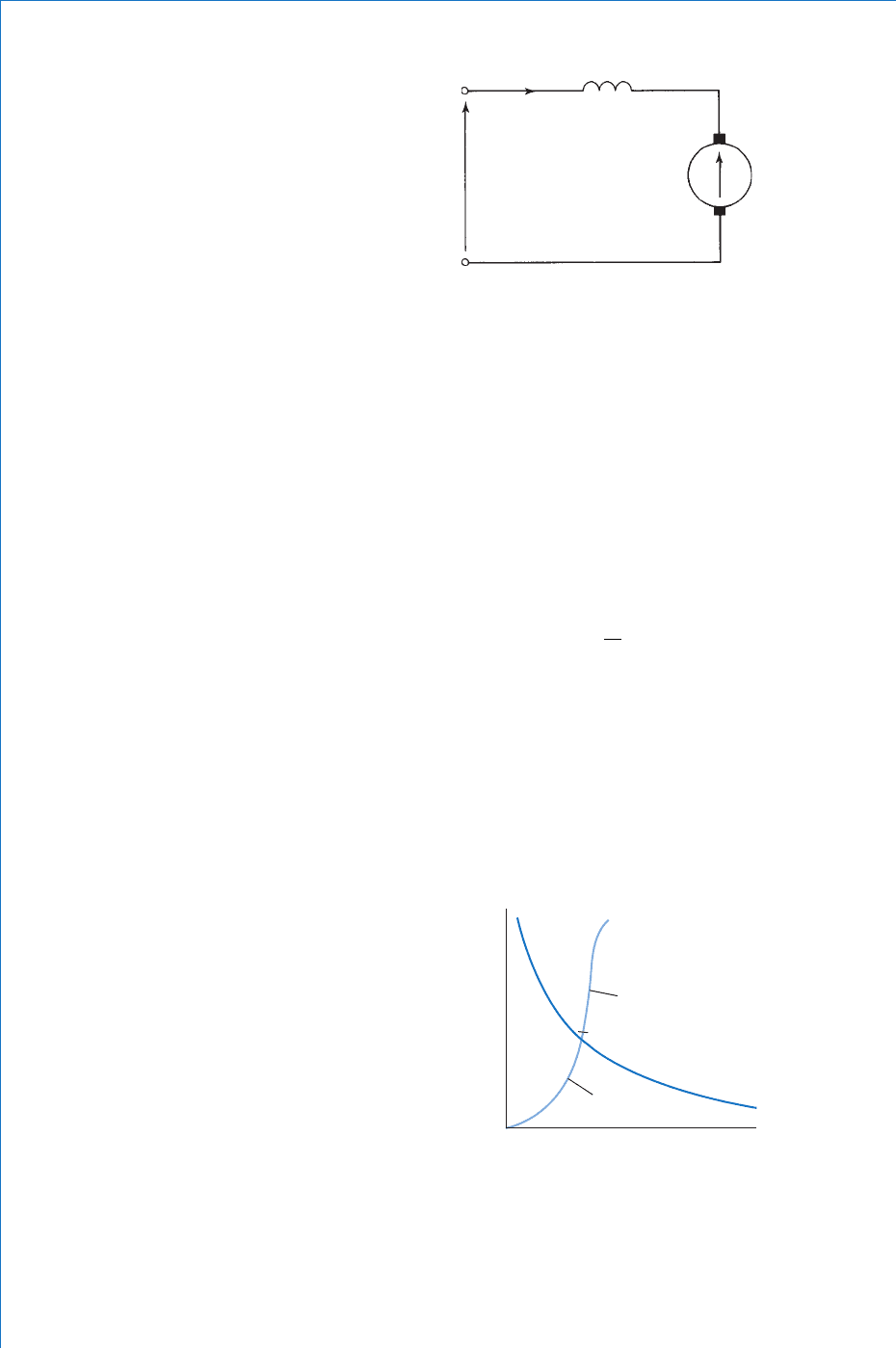
246

Fundamental Electrical and Electronic Principles

Let us assume the following: V  200 V; R

 0.15  ; R

 0.03  ;

 5 A on light-load; I

 50 A on full-load

Light-load: ( ) V

Full-load:

  



200 5 0 15 0 03 199 1

200 50

.. .

(()V0 15 0 03 191..

From the above ﬁ gures, it may be seen that although the armature

current has increased tenfold, the back-emf has decreased by only 4%.

Hence, E

remains sensibly constant.

Since   E

/  , and E

is constant, then:







1...............[ ]

Similarly, T  I

, and since   I

until the onset of magnetic

saturation,

then ............................ .....[2]

and after s



aaturation, ................[ ]TI

 3

Using [1] to [3] above, the speed and torque characteristics shown in

Fig. 7.21 may be deduced.

I

Fig. 7.20

speed or

torque

T  I

Fig. 7.21

Note: From the speed characteristic it is clear that, on very light loads,

the motor speed would be excessive. Theoretically, the no-load speed

D.C. Machines

247

would be inﬁ nite! For this reason a series motor must NEVER be

started unless it is connected to a mechanical load sufﬁ cient to prevent

a dangerously high speed. Similarly, a series motor must not be used to

operate belt-driven machinery, lifting cranes etc., due to the possibility

of the load being suddenly disconnected. If a series motor is allowed

to run on a very light load, its speed builds up very quickly. The

probable outcome of this is the distintegration of the machine, with the

consequent dangers to personnel and plant.

The series motor has a high starting torque due to the ‘ square-law ’

response of the torque characteristic. For this reason, it tends to be

used mainly for traction purposes. For example, an electric train engine

requires a very large starting torque in order to overcome the massive

inertia of a stationary train.

Summary of Equations

Generators:

Shunt generator: I

 I

 I

amp

VEIR

 volt

Series generator: I

 I

amp

VEIR R

aa f

 ( ) volt

Motors:

Shunt motor: E

 V  I

volt

Series motor: E

 V  I

 R

) volt

Speed equation:









rev/second; or rad/second

Torque equation: T  I

newton metre

248 Fundamental Electrical and Electronic Principles

Assignment Questions

1 A shunt generator supplies a current of

85 A at a terminal p.d. of 380 V. Calculate

the generated emf if the armature and  eld

resistances are 0.4  . and 95  respectively.

2 A generator produces an armature current of

50 A when generating an emf of 400 V. If the

terminal p.d. is 390 V, calculate (a) the value

of the armature resistance, and (b) the power

loss in the armature circuit.

3 A d.c. shunt generator supplies a 50 kW load

at a terminal voltage of 250 V. The armature

and  eld circuit resistances are 0.15  and

5 0  respectively. Calculate the generated

emf.

D.C. Transients

Chapter 8

Learning Outcomes

This chapter explains the response of capacitor-resistor, and inductor-resistor circuits, when

they are connected to and disconnected from, a d.c. supply.

On completion of this chapter you should be able to:

1 Show how the current and capacitor voltage in a series C-R circuit varies with time, when

connected to/disconnected from a d.c. supply.

2 Show how the current through, and p.d. across an inductor in a series L-R circuit varies with

time, when connected to/disconnected from a d.c. supply.

3 D e ﬁ ne the term time constant for both types of above circuits.

249

8.1 Capacitor-Resistor Series Circuit (Charging)

Before dealing with the charging process for a C-R circuit, let us

ﬁ rstly consider an analogous situation. Imagine that you need to inﬂ ate

a ‘ ﬂ at ’ tyre with a foot pump. Initially it is fairly easy to pump air

into the tyre. However, as the air pressure inside the tyre builds up,

it becomes progressively more difﬁ cult to force more air in. Also, as

the internal pressure builds up, the rate at which air can be pumped

in decreases. Comparing the two situations, the capacitor (which is to

be charged) is analogous to the tyre; the d.c. supply behaves like the

pump; the charging current compares to the air ﬂ ow rate; and the p.d.

developed between the plates of the capacitor has the same effect as

the tyre pressure. From these comparisons we can conclude that as the

capacitor voltage builds up, it reacts against the emf of the supply, so

slowing down the charging rate. Thus, the capacitor will charge at a

non-uniform rate, and will continue to charge until the p.d. between its

plates is equal to the supply emf. This last point would also apply to

tyre inﬂ ation, when the tyre pressure reaches the maximum pressure

available from the pump. At this point the air ﬂ ow into the tyre would

250

Fundamental Electrical and Electronic Principles

cease. Similarly, when the capacitor has been fully charged, the

charging current will cease.

Let us now consider the C-R charging circuit in more detail. Such a

circuit is shown in Fig. 8.1 . Let us assume that the capacitor is initially

fully discharged, i.e. the p.d. between its plates ( v

) is zero, as will be

the charge, q. Note that the lowercase letters v and q are used because,

during the charging sequence, they will have continuously changing

values, as will the p.d. across the resistor (v

) and the charging current,

i. Thus these quantities are said to have transient values.

‘B’ ‘A’

Fig. 8.1

At some time t  0, let the switch be moved from position ‘ A ’ to

position ‘ B ’ . At this instant the charging current will start to ﬂ ow.

Since there will be no opposition offered by capacitor p.d. (v

 0),

then only the resistor, R, will offer any opposition. Consequently, the

initial charging current ( I

) will have the maximum possible value for

the circuit. This initial charging current is therefore given by:

 amp

(8.1)

Since we are dealing with a series d.c. circuit, then the following

equation must apply at all times:

Ev v

 volt...............[ ]1

thus, at time t  0

0

i.e. the full emf of E volt is developed across the resistor at the instant

the supply is connected to the circuit. Since v

 iR, and at time t  0,

i  I

, this conﬁ rms equation (8.1) above.

Let us now consider the situation when the capacitor has reached its

fully-charged state. In this case, it will have a p.d. of E volt, a charge of

Q coulomb, and the charging current, i  0. If there is no current ﬂ ow

then the p.d. across the resistor, v

 0, and eqn [1] is:

0