Richard S. Gallagher. Computer Visualization: Graphics Techniques for Engineering and Scientific Analysis

Подождите немного. Документ загружается.

contour line.

5. Continue this process for the remaining edges if at least two edges remain. Subsequent points found

will become the first and second endpoints of the next contour line.

A four-vertex quadrilateral can have a maximum of two such contour lines in the case where the isovalue

exists on each of the four edges. Except for the degenerate cases of an isovalue occurring at a vertex or along

an edge, the isovalue will always occur in an even number of points along an element edge.

Previous Table of Contents Next

reserved. Reproduction whole or in part in any form or medium without express written permission of

EarthWeb is prohibited. Read EarthWeb's privacy statement.

Search Tips

Advanced Search

Computer Visualization: Graphics Techniques for Engineering and Scientific Analysis

by Richard S. Gallagher. Solomon Press

CRC Press, CRC Press LLC

ISBN: 0849390508 Pub Date: 12/22/94

Search this book:

Previous Table of Contents Next

Piecewise Contour Interpolation on Isoparametric Elements

In the mid 1970s, Meek and Beer [10] proposed a scheme that expanded the above linear contour calculations

to approximate the true variation of an isovalue contour curve across higher-order elements such as quadratic

elements. This is an important consideration for analysis methods for what is known as the P-version of the

finite element method, where solutions are converged by increasing the order of the equations in the element.

In cases of P-version or higher-order elements, which generally work with a smaller number of large

elements, the variation of the contour line within an element itself may have significance to the analyst.

This approach involves creating a parametric unit square or triangle, which is mapped to the actual element by

use of the element shape functions shown in Figure 4.8. These shape functions, expressed in parametric

coordinates, interpolate defined result values such as those at vertices to other locations within the element.

The variation of the isovalue curve across the element is then determined in a piecewise fashion by

subdividing this unit square or triangle into subareas, and following the path of the contour curve from the

isovalue points on the edges. This method first looks at a subarea containing an isovalue point along an

element edge, and then uses element shape functions to generate a linear interpolation of the vertices of the

element to the vertices of the subarea.

A result value at a parametric location (r, s) on the element can be described as

where the matrix H represents the known interpolation functions, such as the element shape functions

described above, and Ã* represents the vector of vertex values. For a linear 4-vertex surface function, this

interpolation function becomes

while the shape functions for a 4-vertex quadratic (second-order) surface element are:

Title

-----------

Figure 4.8 Parametric mapping of contour lines for quadrilateral and triangular surface areas (From Meek

for vertex nodes

for midside nodes.

These relations are used to interpolate the known result values at element vertices i to the vertices of the

subarea’s parametric r and s locations on the element.

Once the vertex values are interpolated to the subarea, linear interpolation, previously described for the simple

contour line case, is performed to produce a contour line segment across the subarea, as shown in Figure 4.9.

The next computed endpoint of this contour line is then used as a starting point to compute a contour line

segment in the adjacent subarea. This process continues until a contour line endpoint is computed on another

edge of the element—or until one of the previously computed subareas is revisited, indicating the much less

common case where a contour line becomes a closed loop within the element.

Reprinted by permission of John Wiley & Sons, Ltd.)

Direct Contour Generation on Isoparametric Elements

Both of these methods for generating contour lines presume that a piecewise linear approximation will

adequately represent the actual isovalues, and differ largely in the refinement of this linear approximation. An

alternate approach by Akin and Gray [1] uses both the result field and its derivatives for direct generation of

contour lines on an isoparametric surface. This method begins with a starting point Ã

, which can be

computed along an edge as done for previous methods, and then uses a predefined step size to determine the

next point along the contour line. By definition, a contour line represents a path of zero variation in sigma

with respect to the parametric coordinates r and s, or

which can be expressed in (r, s) space as

where dr and ds are the components of the line tangent to the contour line for the known constant step size dL.

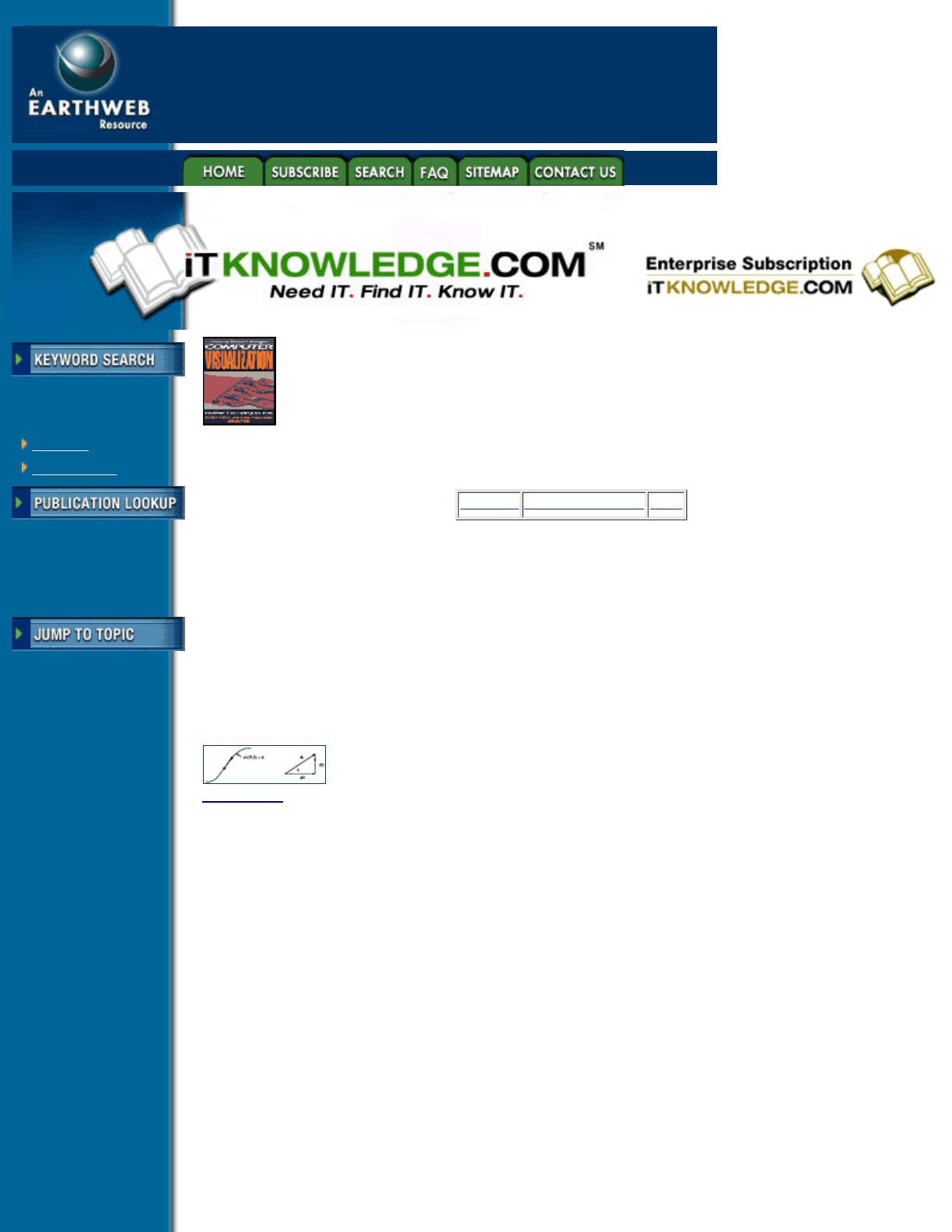
Figure 4.10 shows the tangent segment dL forming an angle ¸ with the parameteric r axis in (r, s) space, and Ä

can be solved by combining equation 4.11 with the relations

and the solution of ðÃ/dr and ðÃ/ds, using the derivatives of the shape functions

Once a value for the angle ¸ is obtained, the next point on the contour path is computed to be at a distance dL

along a tangent line at the angle ¸ within (r, s) space.

The success of this algorithm, i.e., how accurately a piecewise step along the tangent from a contour point will

remain on the actual contour path, depends on the choice of a proper step size—with too large a step, the lines

computed will diverge from the actual contour. Smaller steps are clearly more accurate, but at a cost in

computing time. In the original work on this technique, a step size of

of the perimeter length was

used.

Another potential problem with a direct computational approach is the possibility of an endless loop, in which

a closed contour path within a region never reaches an edge and thereby terminates. In this case, a maximum

number of path points may be used to limit the path computation.

Direct computational techniques such as these can be particularly useful when working with more large-scale,

parametric surfaces as the basic analysis data. At the same time, difficulties such as path divergence and

looping make basic linear approximation within elements or subelements more popular for many cases,

particularly when the elements themselves are linear.

Previous Table of Contents Next

reserved. Reproduction whole or in part in any form or medium without express written permission of

EarthWeb is prohibited. Read EarthWeb's privacy statement.

Search Tips

Advanced Search

Computer Visualization: Graphics Techniques for Engineering and Scientific Analysis

by Richard S. Gallagher. Solomon Press

CRC Press, CRC Press LLC

ISBN: 0849390508 Pub Date: 12/22/94

Search this book:

Previous Table of Contents Next

Extension of Contour Lines to Color-Filled Regions

One of the more common types of contour displays is the contour fringe plot, the color fill analogy to contour

line displays, where discrete color-filled regions correspond to ranges of the result value.

Such displays are conceptually straightforward—color-filled regions are generated between the isovalue lines

at the boundaries of result value ranges. In practice, however, simple linear approaches of fitting polygons to

vertices and edge intersection points, as is often done with contour lines, can lead to overlapping or

ambiguous regions when several result ranges occur in an element with four or more vertices.

Figure 4.10 Tangent to contour line used in step calculation (From Akin and Gray, reference 1, copyright

1977. Reprinted by permission of John Wiley & sons, Ltd.)

A common method of generating linear color polygons within an element involves computing a point location

and interpolated value at the element centroid, and then subdividing the element into triangles defined by the

element edges connected to this centroid. These triangles can be subdivided further into polygons using an

approach such as the following:

1. Determine if all vertex values of the polygon fall within a single contour level range. If so, the

polygon is displayed as a single color corresponding to this range.

2. Take the first pair of vertices (i, j) within the polygon, and determine which contour level values fall

within the result range Ã

to Ã

. Compute the points along this edges corresponding to these individual

contour level values.

3. Proceed in a consistent counter-clockwise or clockwise direction, and repeat step 2 for the remaining

two edges of the polygon.

4. Starting at one vertex, find the points for the contour range values containing this vertex, to form an

n-vertex polygon. Continue in each direction from this vertex and find subsequent contour level points

and vertices within these contour levels to form adjacent polygons. This process produces a set of

disjoint polygons encompassing the element shown in Figure 4.11.

As in directly color coded elements, these polygons can be rendered either directly with a color corresponding

Title

-----------

to the contour result range, or with a color incorporating both the result range and the light source shading

component from the 3-D angle made between the polygon and the light source.

Optimizing Free Faces for Solid Element Contour Displays

Surface-oriented visualization techniques such as contour or fringe displays will be visible only on the

exterior surfaces of an analysis model. When this analysis is composed purely of surface elements, it

generally means that all elements are processed and rendered. On the other hand, analyses performed using

3-D solid elements involve polyhedra in which many result vertices may be completely interior to the model.

For these elements, it is desirable to optimize the model so that only visible exterior faces are processed and

displayed.

Such an optimization of exterior or free faces involves an up-front cost in computation and storage in return

for what is often an order of magnitude increase in the speed of computing and displaying the image.

There are at least two optimization techniques which can be applied to a group of element polygons prior to

display computations:

1. Removal of Duplicate Interior Faces. Polygons from elements in an analysis model are generally

defined by numbered vertices rather than by direct coordinate locations. Such polygons can be sorted

easily to remove faces which are interior to the model by sorting each polygon by the sum of its vertex

numbers, and then comparing polygons with the same sum. Such an approach generally requires

knowing whether the polygons come from surface or solid elements. In the case of solid elements, all

polygons sharing common vertices will be interior to the model and can be removed. In the case of

surface elements, optimization is generally not performed because either polygon may be

visible—examples of this include the case where surfaces of two adjacent materials are joined for

reinforcement purposes in a structural analysis.

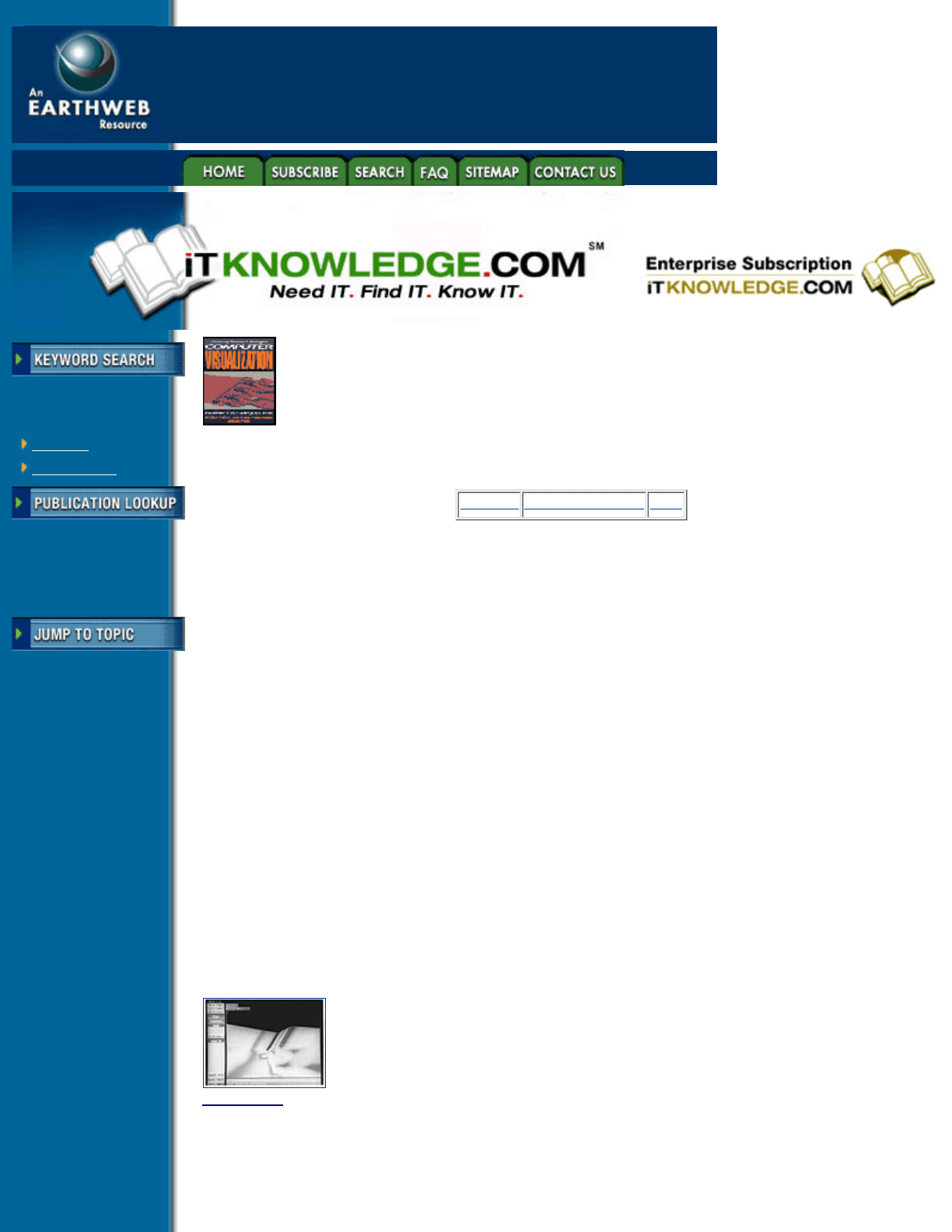
Figure 4.11 Contour fringe display, with discrete color filled result regions (Courtesy MSV National

Superconducting Cyclotron Laboratory).

2. Display-Time Culling of Rearward Faces. When solid elements are defined in a consistent vertex

order, as is generally the case in finite element analysis, the polygon normal can be used to determine

whether the element is facing forward or rearward. Rearward-facing polygons from solid elements are

never visible, and can be removed. This technique is view-specific, and must be repeated whenever

there is a change of viewing direction.

Using the right-hand normal rule, the polygon normal can be defined as shown in Figure 4.12 by obtaining the

cross product of the first and last non-degenerate adjacent edges

where the two edges share a common vertex location, this common vertex is the first one of each edge, and

the order of the cross product is the first edge followed by the last one. If the Cartesian Z component of the

normal is negative in the viewing coordinate system, the polygon is facing rearward and can be removed.

Figure 4.12 Right-hand normal rule for polygon orientation.

Previous Table of Contents Next

reserved. Reproduction whole or in part in any form or medium without express written permission of

EarthWeb is prohibited. Read EarthWeb's privacy statement.

Search Tips

Advanced Search

Computer Visualization: Graphics Techniques for Engineering and Scientific Analysis

by Richard S. Gallagher. Solomon Press

CRC Press, CRC Press LLC

ISBN: 0849390508 Pub Date: 12/22/94

Search this book:

Previous Table of Contents Next

4.3.3 Direct Color Interpolation of Scalar Results

Displays showing scalar results as a continuous tonal variation of color across a surface have a physical

appearance similar to a smoothed version of a contour display, but have little in common with contour

methods from an algorithmic standpoint.

While contours are used as a starting point to generate polygonal color representations across a surface,

accurate color rendering of surface results involves a more direct transformation of the result field into screen

space and a color field. At the same time, a continuous color display of a result value can function like a

discrete contour display by variations in the color map—mapping results to a set of discrete color regions will

produce an area of color fill whose boundaries are analogous to isovalue contour lines.

The two approaches are separated by the change in focus from finding the first occurrence of an isoline within

an element to rendering every point on the elements containing the isovalue. If one tried to create the effect of

contour lines by setting up a color table consisting only of single, discrete colors at isovalue levels, the

isovalues would interpolate to produce thicker or thinner lines as the individual isovalue locations are

computed on each surface.

For a model composed of polygonal faces, the generation of a continuous tonal display begins with a mapping

of the scalar result value to color values at polygon vertices. From this point, the display generation is almost

identical to the process of Gouraud polygon shading, where color values derived from a light source are

interpolated across the polygon. For continuous tonal result display, result-based values are instead

interpolated from the polygon vertices.

Figure 4.13 Continuous tonal color representation of a scalar result (Courtesy Swanson Analysis Systems,

Inc.).

The interpolation itself is performed in a similar fashion to Gouraud shading. Each polygon is projected into

screen space, and a technique known as Bresenham’s algorithm can be used to evaluate the pixels making up

Title

-----------

each scan line through the projected polygon. The color values for these pixels are then interpolated from the

color values obtained where endpoints of the scan line cross the polygon.

As with contour displays, the base colors corresponding to the scalar result can be combined with a light

source-based lightness component to preserve the three-dimensional appearance of an image. Similar to

contour polygons, this lightness is computed at each pixel location as a normalized value

where ¸ is the angle between the normal to the model surface and the light ray, whose position is usually

directly into the Z direction of the screen.

One drawback that inhibits light source shading of continuous tonal displays is that most analysis models are

polygonal representations of an underlying model. The use of polygon normals can cause sharp visual

discontinuities in lightness across polygon boundaries, although the result values themselves should appear

continuous.

The large number of colors required to accomplish light source shading raises another problem. While a range

of 256 simultaneous colors is generally considered sufficient for displaying the scalar result itself, this range

must be multiplied by the number of lightness variations used, generally making true light source shading of

continuous results the domain of hardware supporting “true” color variation based on actual RGB or HLS

values at each pixel.

Correcting for Hardware Interpolation of Scalar Color Values

Continuous tonal result images can be generated on most surface topology representations, as long as these

surfaces can be projected into the pixel space of a graphics display. In practice, however, these surfaces are

generally divided into polygons, and graphics hardware polygon shading capabilities are often used to

interpolate the color across the polygons. Because graphics hardware often breaks polygons into triangles for

shading and rendering, there is an important possible inaccuracy which can occur when sending polygons

with four or more vertices to such hardware. Since each triangle is rendered independently, the order of

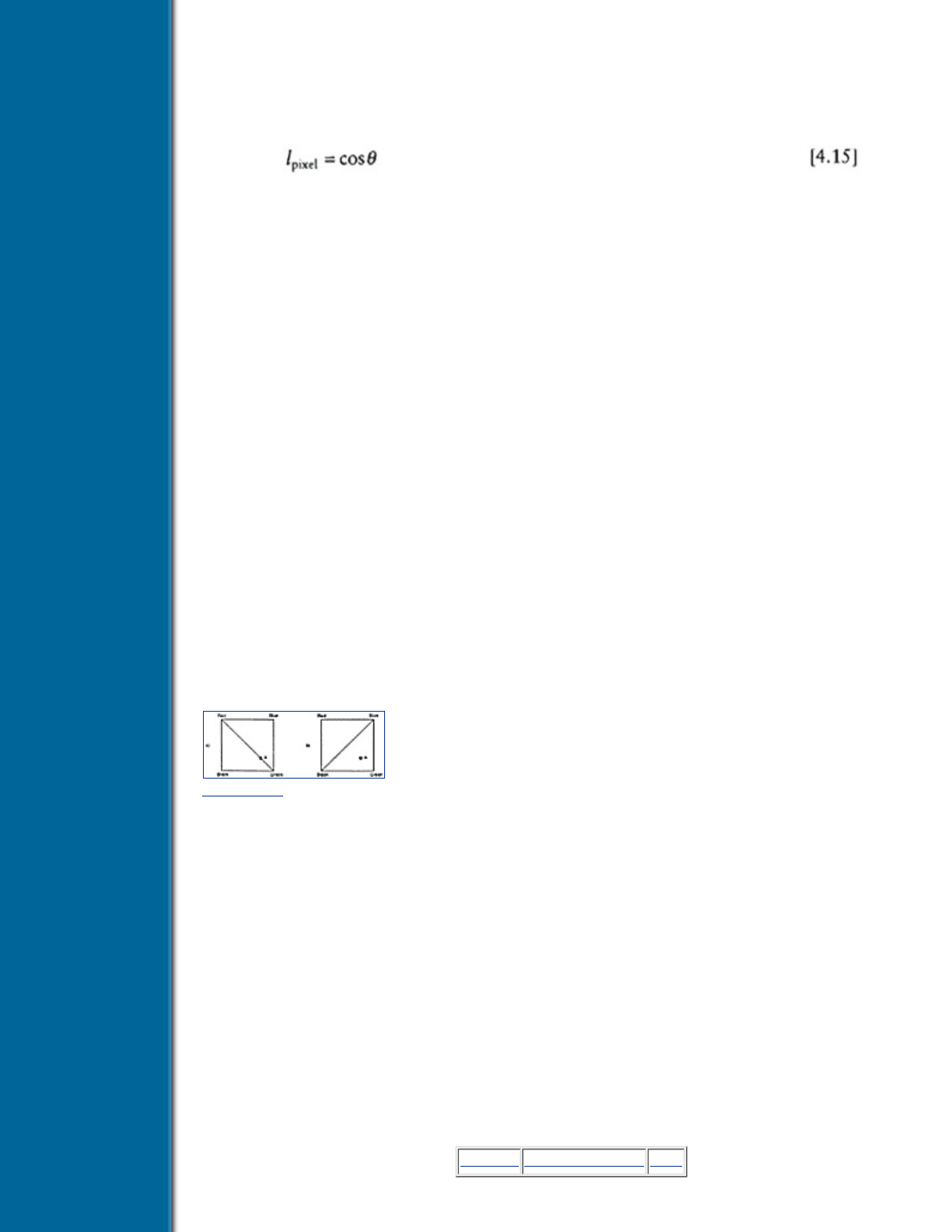
triangulation makes a difference in the distribution of color, as in Figure 4.14.

When results are computed on polygons with four or more vertices, such a triangulation will still produce

correct results across element boundaries and vertices. To produce a more accurate and consistent result

within the elements themselves, they can be subdivided into a more regular pattern of triangles, or into

sub-polygons based on the color distribution within the element.

Figure 4.14 Effect of triangulation on rendering a result polygon. Note that point A will be a shade of orange

(RGB = (0.25, 0.75, 0.0)) in the first case, and a shade of cyan (RGB = (0.0, 0.5, 0.5)) in the second case.

4.4 Three-Dimensional Scalar Fields

As with one-dimensional and two-dimensional scalar fields, one can idealize the display of a

three-dimensional scalar field using discrete symbols at specific locations in space, or use techniques which

show the overall variation of the field.

One requirement unique to the display of a three-dimensional scalar field is the need to see information which

is not on the exterior visible surfaces of the field. This means that the techniques which work for displaying

lower-order fields often display confusing or obscured information in 3-D, and, in the limit, the display of a

continous volume field only reveals its outside surfaces.

As a result, numerous techniques have been specifically developed in recent years for displaying volume

scalar fields. While many of these methods can be generalized to lower dimensions, they share the common

denominator of operating on discrete volume components to produce comprehensible imagery of a 3-D state

of behavior.

Previous Table of Contents Next

reserved. Reproduction whole or in part in any form or medium without express written permission of

EarthWeb is prohibited. Read EarthWeb's privacy statement.